Nonlinear Systems of Equations: Fixed-Point Iteration Method
The Method
Similar to the fixed-point iteration method for finding roots of a single equation, the fixed-point iteration method can be extended to nonlinear systems. This is in fact a simple extension to the iterative methods used for solving systems of linear equations. The fixed-point iteration method proceeds by rearranging the nonlinear system such that the equations have the form.
![Rendered by QuickLaTeX.com \[\begin{split} x_1&=f_1(x_1,x_2,\cdots,x_n)\\ x_2&=f_2(x_1,x_2,\cdots,x_n)\\ &\vdots\\ x_n&=f_n(x_1,x_2,\cdots,x_n) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9cc2add27c24e2f3a2503436d11ee2f9_l3.png)
where ![]() is a nonlinear function of the components
is a nonlinear function of the components ![]() . By assuming an initial guess, the new estimates can be obtained in a manner similar to either the Jacobi method or the Gauss-Seidel method described previously for linear systems of equations. Similar to linear systems of equations, the Euclidean norm can be used to check convergence. So, if the components of the vector
. By assuming an initial guess, the new estimates can be obtained in a manner similar to either the Jacobi method or the Gauss-Seidel method described previously for linear systems of equations. Similar to linear systems of equations, the Euclidean norm can be used to check convergence. So, if the components of the vector ![]() after iteration
after iteration ![]() are
are ![]() , and if after iteration
, and if after iteration ![]() the components are:
the components are: ![]() , then, the stopping criterion would be:
, then, the stopping criterion would be:
![]()
where
![Rendered by QuickLaTeX.com \[\begin{split} \|x^{(i+1)}-x^{(i)}\|&=\sqrt{(x_1^{(i+1)}-x_1^{(i)})^2+(x_2^{(i+1)}-x_2^{(i)})^2+\cdots+(x_n^{(i+1)}-x_n^{(i)})^2}\\ \|x^{(i+1)}\|&=\sqrt{(x_1^{(i+1)})^2+(x_2^{(i+1)})^2+\cdots+(x_n^{(i+1)})^2}\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f500d45c89c156aa0adbac55267bfee1_l3.png)
Note that any other norm function can work as well.
Example
Use the fixed-point iteration method with ![]() to find the solution to the following nonlinear system of equations:
to find the solution to the following nonlinear system of equations:
![]()
Solution
The exact solution in the field of real numbers for this system can actually be obtained using Mathematica as shown in the code below.
View Mathematica CodeClear[x1, x2];
a = Solve[{x1^2 + x1*x2 == 10, x2 + 3 x1*x2^2 == 57}, {x1, x2}, Reals]
N[a]
import sympy as sp
sp.init_printing(use_latex=True)
x1, x2 = sp.symbols('x1 x2')
a = sp.nonlinsolve([x1**2 + x1*x2 - 10, x2 + 3*x1*x2**2 - 57], [x1, x2])
display(a)
The fixed-point iteration numerical method requires rearranging the equations first to the form:
![]()
The following is a possible rearrangement:
![]()
Using an initial guess of ![]() and
and ![]() yields the following:
yields the following:
![]()
For the next iteration, we get:
![]()
Continuing the procedure shows that it is diverging. A different rearrangement for the equations has the form:
![]()
Using the same initial guesses, the first iteration produces:
![]()
The value of ![]() after the first iteration is:
after the first iteration is:
![]()
The following Microsoft Excel table shows that convergence to ![]() and
and ![]() satisfying the required criterion
satisfying the required criterion ![]() is achieved after 9 iterations.
is achieved after 9 iterations.
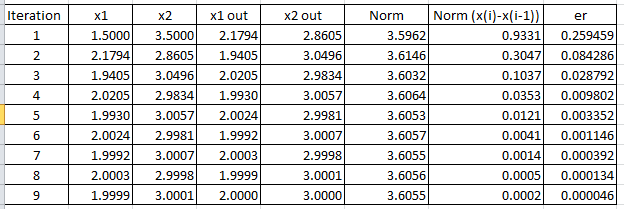
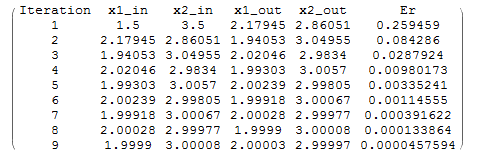
The following code does the same thing in Mathematica to produce the table below:
View Mathematica Codextable = {{1.5, 3.5}};
ErrorTable = {1};
Nmax = 100;
eps = 0.0001;
i = 2;
While[And[ErrorTable[[i - 1]] > eps, i <= Nmax],
x1new = Sqrt[10 - xtable[[i - 1, 1]]*xtable[[i - 1, 2]]];
x2new = Sqrt[(57 - xtable[[i - 1, 2]])/3/x1new];
xnew = {x1new, x2new};
xtable = Append[xtable, xnew];
er = Norm[xnew - xtable[[i - 1]]]/Norm[xnew];
ErrorTable = Append[ErrorTable, er]; i = i + 1];
Title = {"Iteration", "x1_in", "x2_in", "x1_out", "x2_out", "Er"};
T2 = Table[{i, xtable[[i, 1]], xtable[[i, 2]], xtable[[i + 1, 1]], xtable[[i + 1, 2]], ErrorTable[[i + 1]]}, {i, 1, Length[xtable] - 1}];
T2 = Prepend[T2, Title];
T2 // MatrixForm
import numpy as np import pandas as pd xtable = np.array([[1.5, 3.5]]) ErrorTable = [1] Nmax = 100 eps = 0.0001 i = 1 while ErrorTable[i - 1] > eps and i <= Nmax: x1new = np.sqrt(10 - xtable[i - 1, 0]*xtable[i - 1, 1]) x2new = np.sqrt((57 - xtable[i - 1, 1])/3/x1new) xnew = [x1new, x2new] xtable = np.concatenate((xtable,[xnew])) er = np.linalg.norm(xnew - xtable[i - 1])/np.linalg.norm(xnew) ErrorTable.append(er) i += 1 T2 = [[i+1, xtable[i][0], xtable[i][1], xtable[i + 1][0], xtable[i + 1][1], ErrorTable[i + 1]] for i in range(len(xtable)-1)] pd.DataFrame(T2, columns=["Iteration", "x1_in", "x2_in", "x1_out", "x2_out", "Er"])
MATLAB files for the fixed-point iteration example:
Download MATLAB file 1 (fpisystem.m)
Download MATLAB file 2 (g1.m)
Download MATLAB file 3 (g2.m)
The example here shows that the fixed-point iteration method is not guaranteed to give a possible solution. In fact, the initial guess and the form chosen affect whether a solution can be obtained or not. Note that the “FixedPointList” built-in function in Mathematica can be used to implement the method with an initial guess. Notice in the code below how the function ![]() outputs the vector
outputs the vector ![]() as a list and that the second component uses the output of the first component:
as a list and that the second component uses the output of the first component:
g[x_] := (x1 = Sqrt[10 - x[[1]]*x[[2]]]; {x1, Sqrt[(57 - x[[2]])/3/x1]})
FixedPointList[g[#] &, {1.5, 3.5}, 20]
import numpy as np def g(x): x1 = np.sqrt(10 - x[0]*x[1]) return [x1, np.sqrt((57 - x[1])/3/x1)] x = [1.5, 3.5] for i in range(20): print(x) x = g(x)

I am teaching Advance Numerical Analysis at a graduate level in Pakistan and this course is very useful for my students.
Thanks for posting this, it is very useful to have a numerical example for comparison with one’s own code. I arrived at this page via a search for ‘iterative solution of nonlinear equations’ and so had not read your prior material on Gauss-Seidel: it might therefore be good to emphasize that for each equation in the system, the current iteration solution uses the current iteration solutions from the previous equations, e.g. x2 is calculated using the current solution for x1, not the value from the previous iteration. This is clear in the numerical example but not the algebraic statement.
Regards,
Ian
Very nice explanation for methods and problems.