Engineering at Alberta Courses » Basic Numerical Differentiation Formulas

Numerical Differentiation: Basic Numerical Differentiation Formulas

Basic Numerical Differentiation Formulas

The numerical differentiation formulas presented in the Taylor Series section will be repeated here.

Forward Finite Difference

Let $f:[a,b]\rightarrow\mathbb{R}$ be differentiable and let $a\leq x_i < x_{i+1}\leq b$ ,then, using Taylor theorem:

$f(x_{i+1})=f(x_i)+f'(x_i)h+\mathcal{O}(h^2)$

where $h=x_{i+1}-x_i$ . In that case, the forward finite-difference can be used to approximate $f'(x_i)$ as follows:

(1) $\begin{equation*} f'(x_{i})=\frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i}+\mathcal{O}(h) \end{equation*}$

where $\mathcal{O}(h)$ indicates that the error term is directly proportional to the chosen step size $h$ .

Backward Finite Difference

Let $f:[a,b]\rightarrow\mathbb{R}$ be differentiable and let $a\leq x_{i-1}< x_{i}\leq b$ , then, using Taylor theorem:

$f(x_{i-1})=f(x_i)-f'(x_i)h+\mathcal{O} (h^2)$

where $h=x_i-x_{i-1}$ . In this case, the backward finite-difference can be used to approximate $f'(x_i)$ as follows:

(2) $\begin{equation*} f'(x_{i})=\frac{f(x_{i-1})-f(x_i)}{x_{i-1}-x_i}+\mathcal{O} (h) \end{equation*}$

where $\mathcal{O} (h)$ indicates that the error term is directly proportional to the chosen step size $h$ .

Centred Finite Difference

The centred finite difference can provide a better estimate for the derivative of a function at a particular point. If the values of a function $f$ are known at the points $x_{i-1}<x_i<x_{i+1}$ and $x_{i+1}-x_i=x_i-x_{i-1}=h$ , then, we can use the Taylor series to find a good approximation for the derivative as follows:

$\begin{split}f(x_{i+1})&=f(x_i)+f'(x_i)h+\frac{f''(x_i)}{2!}h^2+\mathcal{O}(h^3)\\f(x_{i-1})&=f(x_i)+f'(x_i)(-h)+\frac{f''(x_i)}{2!}h^2+\mathcal{O}(h^3) \end{split}$

subtracting the above two equations and dividing by $h$ gives the following:

$f'(x_i)=\frac{f(x_{i+1})-f(x_{i-1})}{2h}+\mathcal{O}(h^2)$

where $\mathcal{O}(h^2)$ indicates that the error term is directly proportional to the square of the chosen step size $h$ . I.e., the centred finite difference provides a better estimate for the derivative when the step size $h$ is reduced compared to the forward and backward finite differences. Notice that when $x_{i+1}-x_i=x_i-x_{i-1}$ , the centred finite difference is the average of the forward and backward finite difference!

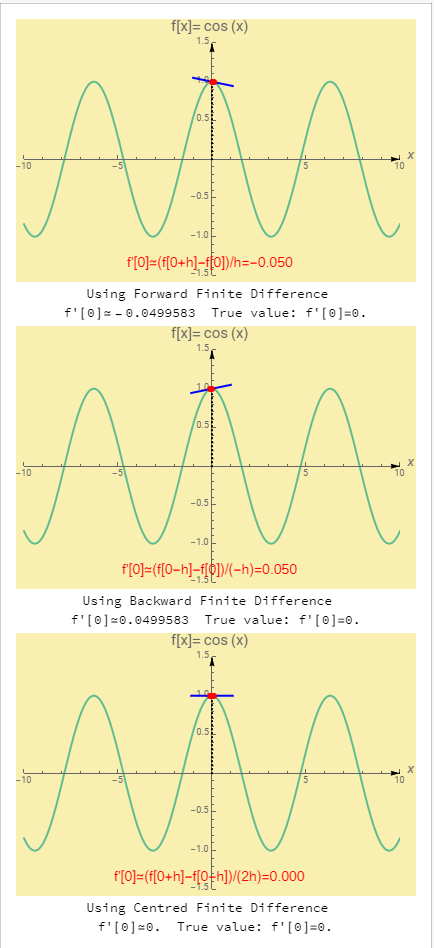
The following tool illustrates the difference between forward, backward, and centred finite difference when calculating the numerical derivative of the function $f(x)=\cos(x)$ at a point $x=x_0$ wit ha step size $h$ . Click on the picture to activate the tool and move the slider to vary the value of $x_0$ and $h$ to see the effect on the calculated deriative. The centred finite difference in most cases provides a closer estimate to the true value of the derivative.

Basic Numerical Differentiation Formulas for Higher Derivatives

The formulas presented in the previous section can be extended naturally to higher-order derivatives as follows.

Forward Finite Difference

Let $f:[a,b]\rightarrow\mathbb{R}$ be differentiable and let $a\leq x_i<x_{i+1}<x_{i+2}\leq b$ , with $h=x_{i+2}-x_{i+1}=x_{i+1}-x_{i}$ , then, using the basic forward finite difference formula for the second derivative, we have:

(3) $\begin{equation*}\begin{split}f''(x_i)&=\frac{f'(x_{i+1})-f'(x_i)}{h}+\mathcal{O}(h)\\ &=\frac{\frac{f(x_{i+2})-f(x_{i+1})}{h}-\frac{f(x_{i+1})-f(x_i)}{h}}{h}+\mathcal{O}(h)\\&=\frac{f(x_{i+2})-2f(x_{i+1})+f(x_i)}{h^2}+\mathcal{O}(h)\end{split}\end{equation*}$

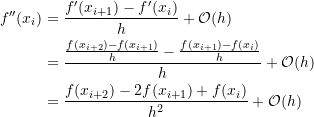
Notice that in order to calculate the second derivative at a point $x_i$ using forward finite difference, the values of the function at two additional points $x_{i+2}$ and $x_{i+1}$ are needed.
Similarly, for the third derivative, the value of the function at another point $x_{i+3}$ with $x_{i+2}<x_{i+3}\leq b$ is required (with the same spacing $h$ ). Then, the third derivative can be calculated as follows:

$\begin{split}f'''(x_i) & = \frac{f''(x_{i+1})-f''(x_i)}{h}+\mathcal O (h)\\&=\frac{\frac{f(x_{i+3})-2f(x_{i+2})+f(x_{i+1})}{h^2}-\frac{f(x_{i+2})-2f(x_{i+1})+f(x_i)}{h^2}}{h}+\mathcal O (h)\\&=\frac{f(x_{i+3})-3f(x_{i+2})+3f(x_{i+1})-f(x_i)}{h^3}+\mathcal O (h)\end{split}$

Similarly, for the fourth derivative, the value of the function at another point $x_{i+4}$ with $x_{i+3}<x_{i+4}\leq b$ is required (with the same spacing $h$ ). Then, the fourth derivative can be calculated as follows:

$\begin{split}f''''(x_i) & = \frac{f'''(x_{i+1})-f'''(x_i)}{h}+\mathcal O (h)\\&=\frac{\frac{f(x_{i+4})-3f(x_{i+3})+3f(x_{i+2})-f(x_{i+1})}{h^3}-\frac{f(x_{i+3})-3f(x_{i+2})+3f(x_{i+1})-f(x_i)}{h^3}}{h} +\mathcal O (h)\\&=\frac{f(x_{i+4})-4f(x_{i+3})+6f(x_{i+2})-4f(x_{i+1})+f(x_i)}{h^4}+\mathcal O (h)\end{split}$

Backward Finite Difference

Let $f:[a,b]\rightarrow\mathbb{R}$ be differentiable and let $a\leq x_{i-2}<x_{i-1}<x_{i}\leq b$ , with $h=x_{i}-x_{i-1}=x_{i-1}-x_{i-2}$ , then, using the basic backward finite difference formula for the second derivative, we have:

(4) $\begin{equation*}\begin{split}f''(x_i)&=\frac{f'(x_{i})-f'(x_{i-1})}{h}+\mathcal{O} (h)\\&=\frac{\frac{f(x_{i})-f(x_{i-1})}{h}-\frac{f(x_{i-1})-f(x_{i-2})}{h}}{h}+\mathcal{O}(h)\\ &=\frac{f(x_{i})-2f(x_{i-1})+f(x_{i-2})}{h^2}+\mathcal{O}(h)\end{split}\end{equation*}$

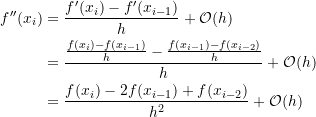
Notice that in order to calculate the second derivative at a point $x_i$ using backward finite difference, the values of the function at two additional points $x_{i-2}$ and $x_{i-1}$ are needed.
Similarly, for the third derivative the value of the function at another point $x_{i-3}$ with $a\leq x_{i-3}< x_{i-2}$ is required (with the same spacing $h$ ). Then, the third derivative can be calculated as follows:

$\begin{split}f'''(x_i) & = \frac{f''(x_{i})-f''(x_{i-1})}{h}+\mathcal O (h)\\&=\frac{\frac{f(x_{i})-2f(x_{i-1})+f(x_{i-2})}{h^2}-\frac{f(x_{i-1})-2f(x_{i-2})+f(x_{i-3})}{h^2}}{h}+\mathcal O (h)\\&=\frac{f(x_{i})-3f(x_{i-1})+3f(x_{i-2})-f(x_{i-3})}{h^3}+\mathcal O (h)\end{split}$

Similarly, for the fourth derivative, the value of the function at another point $x_{i-4}$ with $a\leq x_{i-4} < x_{i-3}$ is required (with the same spacing $h$ ). Then, the fourth derivative can be calculated as follows:

$\begin{split}f''''(x_i) & = \frac{f'''(x_{i})-f'''(x_{i-1})}{h}+\mathcal O (h)\\&=\frac{\frac{f(x_{i})-3f(x_{i-1})+3f(x_{i-2})-f(x_{i-3})}{h^3}-\frac{f(x_{i-1})-3f(x_{i-2})+3f(x_{i-3})-f(x_{i-4})}{h^3}}{h} +\mathcal O (h)\\&=\frac{f(x_{i})-4f(x_{i-1})+6f(x_{i-2})-4f(x_{i-3})+f(x_{i-4})}{h^4}+\mathcal O (h)\end{split}$

Centred Finite Difference

Let $f:[a,b]\rightarrow \mathbb{R}$ be differentiable and let $a\leq x_{i-1}<x_i<x_{i+1} \leq b$ , with a constant spacing $h$ , then, we can use the Taylor theorem for $f(x_{i+1})$ and $f(x_{i-1})$ as follows:

$\begin{split}f(x_{i+1})&=f(x_i)+f'(x_i)h+\frac{f''(x_i)}{2!}h^2+\frac{f'''(x_i)}{3!}h^3+\mathcal{O}(h^4)\\f(x_{i-1})&=f(x_i)+f'(x_i)(-h)+\frac{f''(x_i)}{2!}h^2+\frac{f'''(x_i)}{3!}(-h)^3+\mathcal{O}(h^4) \end{split}$

Adding the above two equations and dividing by $h^2$ gives the following:

(5) $\begin{equation*}f''(x_i)=\frac{f(x_{i+1})-2f(x_i)+f(x_{i-1})}{h^2}+\mathcal O (h^2)\end{equation*}$

which provides a better approximation for the second derivative than that provided by the forward or backward finite difference as the error is directly proportional to the square of the step size.
For the third derivative, the value of the function is required at the points $x_{i-2}$ and $x_{i+2}$ . Assuming all the points to be equidistant with a spacing $h$ , then, the third derivative can be calculated using Equation 5 as follows:

$f'''(x_{i})= \frac{f'(x_{i+1})-2f'(x_i)+f'(x_{i-1})}{h^2}+\mathcal O (h^2)$

Replacing the first derivatives with the centred finite difference value for those:

(6) $\begin{equation*}\begin{split}f'''(x_{i})&= \frac{\frac{f(x_{i+2})-f(x_{i})}{2h}-2\frac{f(x_{i+1})-f(x_{i-1})}{2h}+\frac{f(x_{i})-f(x_{i-2})}{2h}}{h^2}+\mathcal O (h^2)\\&=\frac{f(x_{i+2})-2f(x_{i+1})+2f(x_{i-1})-f(x_{i-2})}{2h^3}+\mathcal O (h^2)\end{split}\end{equation*}$

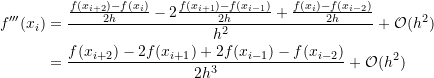
For the fourth derivative, the value of the function at the points $x_{i+2}$ and $x_{i-2}$ is required. Assuming all the points to be equidistant with a spacing $h$ , then, the fourth derivative can be calculated using Equation 5 as follows:

$f''''(x_i)=\frac{f''(x_{i+1})-2f''(x_i)+f''(x_{i-1})}{h^2}+\mathcal O (h^2)$

Using the centred finite difference for the second derivatives (Equation 5) yields:

$\begin{split}f''''(x_i) & = \frac{\frac{f(x_{i+2})-2f(x_{i+1})+f(x_{i})}{h^2}-2\frac{f(x_{i+1})-2f(x_i)+f(x_{i-1})}{h^2}+\frac{f(x_{i})-2f(x_{i-1})+f(x_{i-2})}{h^2}}{h^2} +\mathcal O (h^2)\\&=\frac{f(x_{i+2})-4f(x_{i+1})+6f(x_{i})-4f(x_{i-1})+f(x_{i-2})}{h^4}+\mathcal O (h^2)\end{split}$

Lecture Video

Page Comments

John says:

March 1, 2024 at 9:33 am

It looks like you wrote this in Latex. I’m just getting started with Latex. Would you be willing to share a sample file with me?

Reply
1. Samer Adeeb says:
  
  March 1, 2024 at 11:04 am
  
  This is written in wordpress with “WP QuickLaTeX” pluggin.
  https://wordpress.org/plugins/wp-quicklatex/
  
  Let me know if you require any additional info.
  
  Reply
  1. Samer Adeeb says:
    
    March 1, 2024 at 11:06 am
    
    You can also email me directly if you want samples but this link provides all necessary info:
    https://wordpress.org/plugins/wp-quicklatex/

Open Educational Resources

Numerical Differentiation: Basic Numerical Differentiation Formulas

Basic Numerical Differentiation Formulas

Forward Finite Difference

Backward Finite Difference

Centred Finite Difference

Basic Numerical Differentiation Formulas for Higher Derivatives

Forward Finite Difference

Backward Finite Difference

Centred Finite Difference

Lecture Video

Page Comments

Leave a Reply Cancel reply