Numerical Differentiation: Problems
- Compare the basic formulas and the high-accuracy formulas to calculate the first and second derivatives of
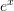 at
at 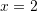 with
with 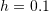 . Clearly indicate the order of the error term in the approximation used. Calculate the relative error
. Clearly indicate the order of the error term in the approximation used. Calculate the relative error 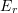 in each case.
in each case. -
A plane is being tracked by radar, and data are taken every two seconds in polar coordinates
 and
and  .
.
Time  (sec.)
(sec.)200 202 204 206 208 210  (rad)
(rad)0.75 0.72 0.70 0.68 0.67 0.66  (m.)
(m.)5120 5370 5560 5800 6030 6240 The vector expression in polar coordinates for the velocity
 and the acceleration
and the acceleration  are given by:
are given by:![Rendered by QuickLaTeX.com \[\begin{split} v&=\frac{\mathrm{d}r}{\mathrm {d}t}e_r+r\frac{\mathrm{d}\theta}{\mathrm {d}t}e_{\theta} \\ a&=\left(\frac{\mathrm{d}^2r}{\mathrm {d}t^2}-r\left(\frac{\mathrm{d}\theta}{\mathrm {d}t}\right)^2\right)e_r+\left(r\frac{\mathrm{d}^2\theta}{\mathrm {d}t^2}+2\frac{\mathrm{d}r}{\mathrm {d}t}\frac{\mathrm{d}\theta}{\mathrm {d}t}\right)e_{\theta} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-10922a84a0121fa5cb1292c8effa6e82_l3.png)
Use the centred finite difference basic formulas to find the velocity and acceleration vectors at
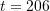 sec. as a function of the unit vectors
sec. as a function of the unit vectors  and
and 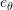 . Then, using the norm of the velocity and acceleration vectors describe the plane speed and the magnitude of its acceleration.
. Then, using the norm of the velocity and acceleration vectors describe the plane speed and the magnitude of its acceleration. - Fick’s first diffusion law states that:
![Rendered by QuickLaTeX.com \[ \mbox{Mass Flux}=-D\frac{\mathrm{d}C}{\mathrm{d}x} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-66b56cf48bcb903e6e4c57212bbd2c1c_l3.png)
where
 is the mass transported per unit area and per unit time with units
is the mass transported per unit area and per unit time with units 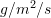 ,
, 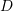 is a constant called the diffusion coefficient given in
is a constant called the diffusion coefficient given in 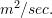 ,
,  is the concentration given in
is the concentration given in  and
and  is the distance in
is the distance in 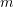 . The law states that the mass transported per unit area and per unit time is directly proportional to the gradient of the concentration (with a negative constant of proportionality). Stated differently, it means that the molecules tend to move towards the area of less concentration. If the concentration of a pollutant in the pore waters of sediments underlying the lake is constant throughout the year and is measured to be:
. The law states that the mass transported per unit area and per unit time is directly proportional to the gradient of the concentration (with a negative constant of proportionality). Stated differently, it means that the molecules tend to move towards the area of less concentration. If the concentration of a pollutant in the pore waters of sediments underlying the lake is constant throughout the year and is measured to be: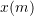
0 1 3  ,
, 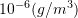
0.06 0.32 0.6 where
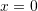 is the interface between the lake and the sediment. By fitting a parabola to the data, estimate
is the interface between the lake and the sediment. By fitting a parabola to the data, estimate 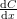 at
at 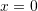 . If the area of interface between the lake and the sediment is
. If the area of interface between the lake and the sediment is 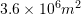 , and if
, and if 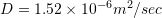 , how much pollutant in
, how much pollutant in  would be transported into the lake over a period of one year?
would be transported into the lake over a period of one year? - The positions in m. of the left and right feet of two squash players (Ramy Ashour and Cameron Pilley) during an 8 second segment of their match in the North American Open in February 2013 are given in the excel sheet provided here. Using a centred finite difference scheme, compare the average and top speed and acceleration between the two players during that segment of the match. Similarly, using a parabolic spline interpolation function, compare the average and top speed and acceleration between the two players. Finally, compare with the average speed of walking for humans.

Hello, I’m currently doing a numerical course very similarly structured to the content in this book, and I find these questions extremely helpful in getting at comprehension on most of the concepts & procedures that we have done.
Is it okay you can send an answer key to these problems?
Thanks,
Atilla.