Nonlinear Systems of Equations: Problems
- Use your implementation of the Newton-Raphson method to find 4 different sets of roots for the following nonlinear system of equations:
![Rendered by QuickLaTeX.com \[ \begin{split} 4-2x_1^2-x_2&=0\\ 8-4x_1-x_2^2&=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e0488a90a30eb942de176f97f6d44249_l3.png)
Use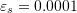 . Compare with the “FindRoot” built-in function in Mathematica.
. Compare with the “FindRoot” built-in function in Mathematica. - Use your implementation of the Newton-Raphson method to find 1 set of roots for the following nonlinear system of equations:
![Rendered by QuickLaTeX.com \[ \begin{split} y=-x^2+x+0.5 \\ y+ 5xy=x^2 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8183a0bbefc20c70bee8e408c2bef07a_l3.png)
Use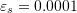 . Compare with the “FindRoot” built-in function in Mathematica.
. Compare with the “FindRoot” built-in function in Mathematica. - Compare the convergence of the Newton-Raphson method and the fixed-point iteration method with initial guesses of
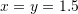 and
and 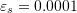 to find a solution to the following nonlinear system of equations:
to find a solution to the following nonlinear system of equations:
![Rendered by QuickLaTeX.com \[ \begin{split} x^2=5-y^2\\ y+1=x^2 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d923a2f4acee849d99d0b6b7a2d6ee36_l3.png)
- Use the Newton-Raphson method to find a solution to the following nonlinear set of equations:
![Rendered by QuickLaTeX.com \[\begin{split} 20x_1^4x_2+3x_2^3=20\\ 20x_1^2x_2^3=1 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f93dda9a4d9af4f5e1bff149835e50d0_l3.png)
Use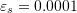
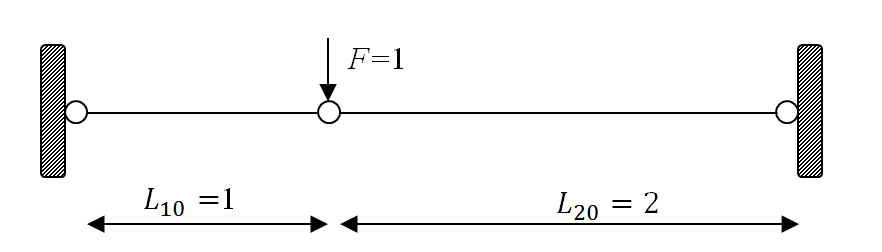
- The following structural system is composed of two truss elements with unit cross sectional area. The left and right supports are hinged supports. The middle connection where the load is applied is also a hinged connection. Find the displacement at equilibrium of the following structural system. Assume a linear material with
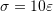 where
where  is the stress in the bar,
is the stress in the bar, 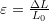 is the corresponding strain, and
is the corresponding strain, and 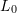 is the initial length. Use the Newton-Raphson method.
is the initial length. Use the Newton-Raphson method.
- Solve the following nonlinear system of equations using the Newton-Raphson method and
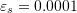
![Rendered by QuickLaTeX.com \[ \begin{split} x_1-x_2-x_3-0.2=0\\ x_2-x_4-0.2=0\\ x_4+x_5-0.2=0\\ -x_5-x_6+x_7-0.2=0\\ x_3+x_6-0.2=0\\ 20|x_2|x_2-30|x_3|x_3+20|x_4|x_4-20|x_5|x_5+40|x_6|x_6=0\\ 60|x_1|x_1+30|x_3|x_3-40|x_6|x_6-30|x_7|x_7-10=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-057540dd57eb99ef1e3a81b4351d4f76_l3.png)
Hint, if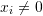 :
:
![Rendered by QuickLaTeX.com \[ \frac{\partial |x_i|x_i}{\partial x_i}=2|x_i| \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-aba34ffc688d7a19f40fb87589221ad9_l3.png)
- The following three equations describe a plane, a hyperbolic paraboloid (i.e., a saddle function), and a sphere, respectively.
![Rendered by QuickLaTeX.com \[ \begin{split} f_1(x,y,z)&=x-y-z+1=0\\ f_2(x,y,z)&=x^2+y-z^2=0\\ f_3(x,y,z)&=x^2+y^2+z^2-4=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-288cb9aaf7c9a3b91b50eee1ee89fc20_l3.png)
Find the coordinates of the two points at which the three surface plots intersect.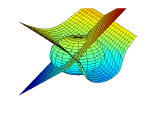
3D plot of the sphere, the paraboloid, and the plane intersecting each other
- Solve the following system of nonlinear equations using the Newton-Raphson method.
![Rendered by QuickLaTeX.com \[y-\cosh(x) = 0 \qquad \text{and} \qquad x^2 + y^2 - 2 = 0\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-872463fcf2f9a666caf38a6c9d588aae_l3.png)
Plot the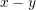 curves for each equation.
curves for each equation.
9. Use the Newton-Raphson method to solve the following linear system of equations
![Rendered by QuickLaTeX.com \[\begin{bmatrix} 10 && 4 && 2 && 4\\ 5 && 1 && -2 && 4 \\ 1 && 5 && 1 && -1 \\0 && 6 && -2 && 2 \end{bmatrix} \begin{bmatrix}x \\ y \\ z \\ w \end{bmatrix} = \begin{bmatrix}25 \\ 14 \\ 10 \\ 8 \end{bmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6e46133706919068f32b502d025f10f5_l3.png)
Provide comments on the behaviour of this method for a linear system of equations with regards to the solution procedure and number of iterations to reach a certain accuracy. Explain the reasons or causes of this behaviour.
