Engineering at Alberta Courses

Python Lab Tutorials: Lab 10

Consider the following integral

$\mbox{erf}(a)=\frac{2}{\sqrt{\pi}}\int_{0}^{a}e^{-x^2}\,\mathrm{d}x$

with $a=1.5$

Use Sympy’s built-in numerical integration “integrate” function to calculate an approximation to the true value of the integral. Consider this to be the true value.
Plot 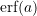$\mbox{erf}(a)$ for $y\in[-2,2]$
Using the midpoint rectangle rule, provide a table with the following columns: n,h,I_2,|E| with $n=1,2,4,8,16,…,128$
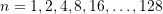
Using the trapezoidal rule, provide a table with the following columns: n,h,I_T,|E| with $n=1,2,4,8,16,…,128$
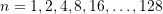
Using Simpson’s 1/3 rule, provide a table with the following columns: n,h,I_S1,|E| with $n=1,2,4,8,16,…,128$
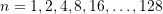
Using Simpson’s 3/8 rule, provide a table with the following columns: n,h,I_S2,|E| with $n=1,2,4,8,16,…,128$
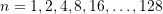
Comment on the accuracy obtained using each method