Taylor Series: Examples and Problems
Examples
Example 1
Apply Taylor’s Theorem to the function ![]() defined as
defined as ![]() to estimate the value of
to estimate the value of ![]() . Use
. Use ![]() . Estimate an upper bound for the error.
. Estimate an upper bound for the error.
Solution
The Taylor approximation of the function ![]() around the point
around the point ![]() is given as follows:
is given as follows:
![]()
If ![]() terms are used (including
terms are used (including ![]() ), then the upper bound for the error is:
), then the upper bound for the error is:
![]()
With ![]() , an upper bound for the error can be calculated by assuming
, an upper bound for the error can be calculated by assuming ![]() . That’s because the absolute values of the derivatives of
. That’s because the absolute values of the derivatives of ![]() attain their maximum value in the interval
attain their maximum value in the interval ![]() at 4. The derivatives of
at 4. The derivatives of ![]() have the following form:
have the following form:
![Rendered by QuickLaTeX.com \[\begin{split} f'(x)&=\frac{1}{2\sqrt{x}}\\ f''(x)&=\frac{-1}{4x^{\frac{3}{2}}}=\frac{-1}{4x\sqrt{x}}\\ f'''(x)&=\frac{3}{8x^{\frac{5}{2}}}=\frac{3}{8x^2\sqrt{x}}\\ f''''(x)&=\frac{-15}{16x^{\frac{7}{2}}}=\frac{-15}{16x^3\sqrt{x}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9a8fdd6b5e8ef72e4ebdcf3a27418764_l3.png)
The derivatives of the function evaluated at the point ![]() can be calculated as:
can be calculated as:
![Rendered by QuickLaTeX.com \[\begin{split} f'(4)&=\frac{1}{4}\\ f''(4)&=\frac{-1}{32}\\ f'''(4)&=\frac{3}{256}\\ f''''(4)&=\frac{-15}{2048} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f8b84ec6483460ea038f8902879991f4_l3.png)
If two terms are used, then:
![]()
In this case, the upper bound for the error is:
![]()
Using Mathematica, the square root of ![]() approximated to 4 decimal places is
approximated to 4 decimal places is ![]() . Therefore, the error when two terms are used is:
. Therefore, the error when two terms are used is:
![]()
which satisfies that the actual error is less the upper bound:
![]()
If three terms are used, then:
![]()
In this case, the upper bound for the error is:
![]()
The actual error in this case is indeed less than the upper bound:
![]()
The following code provides a user-defined function for the Taylor series having the following inputs: a function ![]() , the value of
, the value of ![]() , the value of
, the value of ![]() , and the number of terms
, and the number of terms ![]() including the constant term.
including the constant term.
Clear[x]
Taylor[f_, xi_, a_, n_] := Sum[(D[f, {x, i}] /. x -> a)/i!*(xi - a)^i, {i, 0, n - 1}]
f = (x)^(0.5);
a = Table[{i, Taylor[f, 5, 4, i]}, {i, 2, 21}];
a // MatrixForm
import math
import sympy as sp
x = sp.symbols('x')
def taylor(f,xi,a,n):
return sum([(f.diff(x, i).subs(x,a))/math.factorial(i)*(xi - a)**i for i in range(n)])
f = x**(0.5)
m = []
for i in range(2,22):
m.append([i,taylor(f,5,4,i)])
display(sp.Matrix(m))
You can download the MATLAB file below which provides the solution to this question.
Example 2
Apply Taylor’s Theorem to the function ![]() defined as
defined as ![]() to estimate the value of
to estimate the value of ![]() and
and ![]() . Use
. Use ![]() . Estimate an upper bound for the error.
. Estimate an upper bound for the error.
Solution
First, we will calculate the numerical solution for the ![]() and
and ![]() :
:
![]()
The Taylor approximation around ![]() is given as:
is given as:
![]()
If ![]() terms are used (including
terms are used (including ![]() ) and if
) and if ![]() , then the upper bound of the error is:
, then the upper bound of the error is:
![]()
If ![]() , then, the upper bound of the error is:
, then, the upper bound of the error is:
![]()
The derivatives of the function are given by:
![Rendered by QuickLaTeX.com \[ \begin{split} f(x)&=(1-x)^{0.5}\\ f'(x)&=-\frac{0.5}{(1-x)^{0.5}}\\ f''(x)&=-\frac{0.25}{(1-x)^{1.5}}\\ f'''(x)&=-\frac{0.375}{(1-x)^{2.5}}\\ f''''(x)&=-\frac{0.9375}{(1-x)^{3.5}}\\ f^{(5)}(x)&=-\frac{3.28125}{(1-x)^{4.5}}\\ f^{(6)}(x)&=-\frac{14.7656}{(1-x)^{5.5}}\\ f^{(7)}(x)&=-\frac{81.2109}{(1-x)^{6.5}}\\ f^{(8)}(x)&=-\frac{527.871}{(1-x)^{7.5}} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-190593249346463c20dfff83f8444274_l3.png)
when evaluated at ![]() these have the values:
these have the values:
![Rendered by QuickLaTeX.com \[\begin{split} f(0)&=1\\ f'(0)&=-0.5\\ f''(0)&=-0.25\\ f'''(0)&=-0.375\\ f''''(0)&=-0.9375\\ f^{(5)}(0)&=-3.28125\\ f^{(6)}(0)&=-14.7656\\ f^{(7)}(0)&=-81.2109\\ f^{(8)}(0)&=-527.871 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c0ee12ba22152bd151f097e4b85885e4_l3.png)
For ![]() , and using two terms:
, and using two terms:
![]()
Using three terms:
![]()
Using four terms:
![Rendered by QuickLaTeX.com \[ \begin{split} f(0.1)&\approx f(0)+f'(0)(0.1)+\frac{f''(0)}{2!}(0.1)^2+\frac{f'''(0)}{3!}(0.1)^3\\ &=1-0.5\times 0.1-\frac{0.25}{2}0.1^2-\frac{0.375}{3\times 2}0.1^3 = 0.9486875 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-47eba30c9945bc0e80fb8568bc52b531_l3.png)
The terms are getting closer to each other and four terms provide a good approximation. The error term in the theorem gives an upper bound for ![]() as follows:
as follows:
![]()
The maximum value would be obtained for ![]() . Therefore:
. Therefore:
![]()
Indeed, the actual value of the error is less than the upper bound:
![]()
For ![]() , the Taylor series for this function around
, the Taylor series for this function around ![]() doesn’t give a very good approximation as will be shown here but rather keeps oscillating. First, using two terms:
doesn’t give a very good approximation as will be shown here but rather keeps oscillating. First, using two terms:
![]()
Using three terms:
![]()
Using four terms:
![Rendered by QuickLaTeX.com \[\begin{split} f(-2)&\approx f(0)+f'(0)(-2)+\frac{f''(0)}{2!}(-2)^2+\frac{f'''(0)}{3!}(-2)^3\\ &=1-0.5\times (-2)-\frac{0.25}{2}(-2)^2-\frac{0.375}{3\times 2}(-2)^3 \\ &= 2 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2aa35475bf33994fc195580a12b50fa1_l3.png)
Using five terms:
![Rendered by QuickLaTeX.com \[\begin{split} f(-2)&\approx f(0)+f'(0)(-2)+\frac{f''(0)}{2!}(-2)^2+\frac{f'''(0)}{3!}(-2)^3+\frac{f''''(0)}{4!}(-2)^4\\ &=1-0.5\times (-2)-\frac{0.25}{2}(-2)^2-\frac{0.375}{3\times 2}(-2)^3 -\frac{0.9375}{4\times 3\times 2}(-2)^4\\ &= 1.375 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-81ea35a827bebb3575f0d9f774307ea7_l3.png)
Using six terms:
![Rendered by QuickLaTeX.com \[\begin{split} f(-2)&\approx f(0)+f'(0)(-2)+\frac{f''(0)}{2!}(-2)^2+\frac{f'''(0)}{3!}(-2)^3+\frac{f''''(0)}{4!}(-2)^4+\frac{f'''''(0)}{5!}(-2)^5\\ &=1-0.5\times (-2)-\frac{0.25}{2}(-2)^2-\frac{0.375}{3\times 2}(-2)^3 -\frac{0.9375}{4\times 3\times 2}(-2)^4-\frac{-3.28125}{5\times 4\times 3\times 2}(-2)^5\\ &=2.25 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b26118a8eda6e7a40d09ebaf1a188ad6_l3.png)
In fact, the following table gives the values up to 21 terms. It is clear that the Taylor series is diverging.

The error term in the theorem gives an upper bound for ![]() when six terms are used as follows:
when six terms are used as follows:
![]()
The maximum value will be obtained when ![]() :
:
![]()
This is a large upper bound and indicates that using six terms is not giving a good approximation. In general, the Taylor series works best if the distance between ![]() and
and ![]() is as small as possible. For some functions, like
is as small as possible. For some functions, like ![]() ,
, ![]() , and
, and ![]() , the Taylor series always converges. However, for functions with square roots, the Taylor series converges when
, the Taylor series always converges. However, for functions with square roots, the Taylor series converges when ![]() is relatively close to
is relatively close to ![]() . There are some analytical conditions that would indicate the radius of convergence
. There are some analytical conditions that would indicate the radius of convergence ![]() of a Taylor series; however, this is beyond the scope of this course!
of a Taylor series; however, this is beyond the scope of this course!
The following code provides a user-defined function for the Taylor series having the following inputs: a function ![]() , the value of
, the value of ![]() , the value of
, the value of ![]() , and the number of terms
, and the number of terms ![]() including the constant term.
including the constant term.
Clear[x]
Taylor[f_, xi_, a_, n_] := Sum[(D[f, {x, i}] /. x -> a)/i!*(xi - a)^i, {i, 0, n-1}]
f = (1 - x)^(0.5);
a = Table[{i, Taylor[f, -2, 0, i]}, {i, 2, 21}];
a // MatrixForm
a = Table[{i, Taylor[f, 0.1, 0, i]}, {i, 2, 21}];
a // MatrixForm
import math
import sympy as sp
x = sp.symbols('x')
def taylor(f,xi,a,n):
return sum([(f.diff(x, i).subs(x,a))/math.factorial(i)*(xi - a)**i for i in range(n)])
f = (1 - x)**(0.5)
m1 = []; m2 = []
for i in range(2,22):
m1.append([i,taylor(f, -2, 0, i)])
m2.append([i,taylor(f, 0.1, 0, i)])
display(sp.Matrix(m1))
display(sp.Matrix(m2))
Example 3
Use zero through fourth order Taylor’s series expansion to approximate the value of the function ![]() defined as
defined as ![]() at
at ![]() . Use
. Use ![]() . Calculate the error associated with each expansion.
. Calculate the error associated with each expansion.
Solution
The true value of the function at ![]() is given by:
is given by:
![]()
The zero order Taylor series expansion around ![]() has the following form:
has the following form:
![]()
The error in this case is given by:
![]()
The first order Taylor series expansion around ![]() has the following form:
has the following form:
![]()
The error in this case is given by:
![]()
The second order Taylor series expansion around ![]() has the following form:
has the following form:
![]()
The error in this case is given by:
![]()
The third order Taylor series expansion around ![]() has the following form:
has the following form:
![Rendered by QuickLaTeX.com \[\begin{split} f(1)& \approx f(0)+(1-0)f'(0)+\frac{(1-0)^2}{2!}f''(0)+\frac{(1-0)^3}{3!}f'''(0)\\ & = 1.2+(1-0)(-0.25)+\frac{1}{2}(-1)+\frac{1}{6}(-0.9)\\ &=0.3 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a6abb7413f69594e5072184e1223ad25_l3.png)
The error in this case is given by:
![]()
The fourth order Taylor series expansion around ![]() has the following form:
has the following form:
![Rendered by QuickLaTeX.com \[\begin{split} f(1)&\approx f(0)+(1-0)f'(0)+\frac{(1-0)^2}{2!}f''(0)+\frac{(1-0)^3}{3!}f'''(0)+\frac{(1-0)^4}{4!}f''''(0)\\ & = 1.2+(1-0)(-0.25)+\frac{1}{2}(-1)+\frac{1}{6}(-0.9)+\frac{1}{24}(-2.4)\\ & =0.2 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7c26a136b68adec2c4635c8a6d848aa5_l3.png)
The error in this case is given by:
![]()
It is important to note that the error reduces to zero when using the fourth order Taylor series approximation. That is because the fourth order Taylor series approximation of a fourth order polynomial function is identical to the function itself. You can think of this as follows, the zero order Taylor approximation provides a “constant” function approximation. The second order Taylor approximation provides a parabolic function approximation while the third order provides a cubic function approximation. The nth Taylor series approximation of a polynomial of degree “n” is identical to the function being approximated!
You can download the MATLAB file below which provides the solution to this question.
Problems
- Use the Taylor series for the function
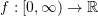 defined as
defined as 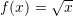 to estimate the value of
to estimate the value of 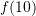 . Use
. Use 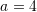 once and
once and 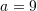 for another time. Estimate an upper bound for the error for each approximation. Comment on the behaviour of the Taylor series of this function. (hint: For this particular function using a Taylor expansion around
for another time. Estimate an upper bound for the error for each approximation. Comment on the behaviour of the Taylor series of this function. (hint: For this particular function using a Taylor expansion around 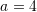 should not give a proper approximation for
should not give a proper approximation for 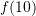 because 10 and 4 are far from each other)
because 10 and 4 are far from each other) - Using the Taylor series and setting
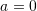 , derive the polynomial forms of the functions listed in the MacLaurin series section.
, derive the polynomial forms of the functions listed in the MacLaurin series section. - Use Taylor’s Theorem to find an estimate for
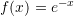 at
at 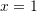 with
with 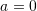 . Employ the zero-, first-,
. Employ the zero-, first-,
second-, and third-order versions and compute the truncation error for each case. - Using the MacLaurin series expansion for
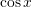 , find an approximation for
, find an approximation for 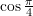 as a function of the number of terms up to 5 terms. For each case, find the relative error
as a function of the number of terms up to 5 terms. For each case, find the relative error 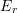 and the relative approximate error
and the relative approximate error 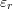 .
. - Use zero- through third-order Taylor series expansions to predict
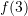 for
for
![Rendered by QuickLaTeX.com \[ f(x) = 25x^3-6x^2+7x-88 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e0e7f2317b87a88441b09ebd97a20210_l3.png)
assuming that
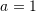 . Compute
. Compute 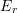 for each approximation.
for each approximation. - Derive the MacLaurin series for the following functions:
![Rendered by QuickLaTeX.com \[ f_1(x)=\frac{1}{1+x}\quad f_2(x)=\frac{1}{1-x}\quad f_3(x)=\frac{1}{1+x^2} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-36fbc6af151cf3038157138f3cbad502_l3.png)
Note: The resulting series are only convergent for
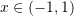
- Derive the MacLaurin series for the following functions:
![Rendered by QuickLaTeX.com \[ f_1(x)=\ln{(1+x)}\quad \quad f_2(x)=\tan^{-1}{x} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d86201ed55f9cca5ae501ff687de9e10_l3.png)
Note: The resulting series are only convergent for
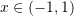

This is a comment
how to activate first example’s code in matlab. it gives error everytime. please help
Many thanks for sharing these Numerical Methods OpenCourse resources to the learning community! Dr. Lindsey Westover’s videos are very well presented and narrated – she’s a natural teacher🙏