Polynomial Interpolation: Newton Interpolating Polynomials

Newton Interpolating Polynomials

As stated in the introduction, the matrix formed in Equation 1 can be ill-conditioned and difficult to find an inverse for. A simpler method can be used to find the interpolating polynomial using Newton’s Interpolating Polynomials formula for fitting a polynomial of degree through data points with :

where the coefficients are defined recursively using the divided differences as follows:

This recursive divided differences are illustrated in the following table:

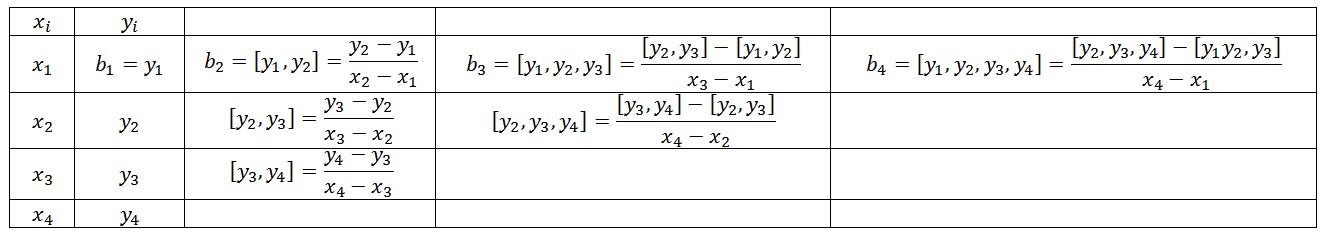
The following Mathematica code implements a recursive function “f” that produces the coefficients .

Data = {{1, 3}, {4, 5}, {5, 6}, {6, 8}, {7, 8}};
f[anydata_] := If[Length[anydata] == 1, anydata[[1, 2]], If[Length[anydata] ==2, (anydata[[2, 2]] - anydata[[1, 2]])/(anydata[[2, 1]] -anydata[[1, 1]]), (f[Drop[anydata, 1]] - f[Drop[anydata, -1]])/(anydata[[Length[anydata], 1]] - anydata[[1, 1]])]]
NP[anydata_] := Sum[f[anydata[[1 ;; i]]]*Product[(x - anydata[[j, 1]]), {j, 1, i - 1}], {i, 1, Length[anydata]}]
(*Using the Newton polynomial function*)
y = Expand[NP[Data]]
(*Using the interpolating polynomial built-in function*)
y2 = Expand[InterpolatingPolynomial[Data, x]]

import numpy as np
import sympy as sp
sp.init_printing(use_latex=True)

Data = [(1, 3), (4, 5), (5, 6), (6, 8), (7, 8)]
x = sp.symbols('x')
def f(anydata):
  if len(anydata) == 1:
    return anydata[0][1]
  elif len(anydata) == 2:
    return (anydata[1][1] - anydata[0][1])/(anydata[1][0] -anydata[0][0])
  else:
    return (f(anydata[1:]) - f(anydata[:-1]))/(anydata[len(anydata)-1][0] - anydata[0][0])
def NP(anydata):
  return sum([f(anydata[0:i+1])*np.prod([(x - anydata[j][0]) for j in range(i)]) for i in range(len(anydata))])
# Using the Newton polynomial function
display("y: ",sp.expand(NP(Data)))
# Using the interpolating polynomial built-in function
display("y2: ",sp.interpolate(Data, x))

Newton’s formula for generating an interpolating polynomial adopts a form similar to that of a Taylor’s polynomial but is based on finite differences rather than the derivatives. I.e., the coefficients are calculated using finite difference. One advantage to this form is that the degree of a Newton’s interpolating polynomial can be increased (or decreased) automatically by adding (or removing) more terms corresponding to new points without discarding existing terms.

Example 1

Using Newton’s interpolating polynomials, find the interpolating polynomial to the data: (1,1),(2,5).

Solution

We have two data points, so, we will create a polynomial of the first degree. Therefore:

Therefore, the interpolating polynomial has the form:

Example 2

Using Newton’s interpolating polynomials, find the interpolating polynomial to the data: (1,1),(2,5),(3,2).

Solution

We have three data points, so, we will create a polynomial of the second degree. Therefore:

Therefore, the interpolating polynomial has the form:

Example 3

Using Newton’s interpolating polynomials, find the interpolating polynomial to the data: (1,1),(2,5),(3,2),(3.2,7),(3.9,4).

Solution

The divided difference table for these data points were created in excel as follows:

Therefore, the Newton’s Interpolating Polynomial has the form:

Lecture Video