Polynomial Interpolation: Problems

1. Derive the Newton interpolating polynomial and the Lagrange polynomial formulas.
2. Find 5 examples where an engineer could have some discrete experimental observations 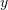for specific instances of a variable and would be seeking a relationship to describe 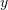versus .
3. The following data points provide the distance in m on a plate and the corresponding measured temperature in Celsius (0,80), (2,53.5), (4,38.43), (6,30.39), (8,30). Find an interpolating polynomial that fits through all the data points. Plot the curve showing the interpolating polynomial and mark the data points on the curve. Use the interpolating polynomial to estimate the temperature at .
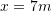4. Using the same data given in the previous problem, estimate the temperature at 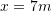using linear, quadratic, third, and fourth order Newton polynomial interpolation. For each case, pick enough points for the order of interpolation. Do you get the same answer? Comment on the results.
5. Repeat the previous problem using linear, quadratic, third order, and fourth Lagrange polynomial interpolation. Comment on your answer.
6. The following data provides the average tuition fees in Canadian dollars for engineering students in Alberta from 2010 to 2014 (2010,5401),(2012,5886), (2013,5871), (2014,5929). Use an interpolating polynomial to find an estimate for the tuition fees in 2011. (Data source). Compare your result to the actual value reported by Stats Canada which is: 5815 Canadian dollars.
7. The concentration of a certain toxin in a system of lakes has been monitored at intervals from 1993 to 2003 and was reported as (1993,120), (1995, 127), (1997, 130), (1999, 152), (2001, 182), (2003,198). Using polynomial interpolation, estimate the concentration in 2002. What happens if you remove the first two data points, do you get the same estimate? Comment on your answer.