Curve Fitting: Nonlinear Regression
Nonlinear Regression
In nonlinear regression, the model function ![]() is a nonlinear function of
is a nonlinear function of ![]() and of the parameters
and of the parameters ![]() . Given a set of
. Given a set of ![]() data points
data points ![]() with
with ![]() , curve fitting starts by assuming a model
, curve fitting starts by assuming a model ![]() with
with ![]() parameters. The parameters can be obtained by minimizing the least squares:
parameters. The parameters can be obtained by minimizing the least squares:
![]()
In order to find the parameters of the model that would minimize ![]() ,
, ![]() equations of the following form are solved:
equations of the following form are solved:
![]()
Since ![]() is nonlinear in the coefficients, the
is nonlinear in the coefficients, the ![]() equations formed are also nonlinear and can only be solved using a nonlinear equation solver method such as the Newton Raphson method described before. We are going to rely on the built-in NonlinearModelFit function in Mathematica that does the required calculations.
equations formed are also nonlinear and can only be solved using a nonlinear equation solver method such as the Newton Raphson method described before. We are going to rely on the built-in NonlinearModelFit function in Mathematica that does the required calculations.
Example 1
The following data describes the yield strength ![]() and the plastic strain
and the plastic strain ![]() obtained from uniaxial experiments where the first variable is the plastic strain and the second variable is the corresponding yield strength: (0.0001,204.18),(0.0003,226.4),(0.0015,270.35),(0.0025,276.86),(0.004,296.86),(0.005,299.3),(0.015,334.65),(0.025,346.56),(0.04,371.81),(0.05,377.45),(0.1,398.01),(0.15,422.45),(0.2,434.42).
obtained from uniaxial experiments where the first variable is the plastic strain and the second variable is the corresponding yield strength: (0.0001,204.18),(0.0003,226.4),(0.0015,270.35),(0.0025,276.86),(0.004,296.86),(0.005,299.3),(0.015,334.65),(0.025,346.56),(0.04,371.81),(0.05,377.45),(0.1,398.01),(0.15,422.45),(0.2,434.42).
Use the NonlinearModelFit function in Mathematica to find the best fit for the data assuming the relationship follows the form:
![]()
Solution
While this model can be linearized as described in the previous section, the NonlinearModelFit will be used. The array of data is input as a list in the variable Data. The NonlinearModelFit function is then used and the output is stored in the variable: “model”. The form of the best fit function is evaluated using the built-in function Normal[model]. ![]() can be evaluated as well as shown in the code below. The values of
can be evaluated as well as shown in the code below. The values of ![]() and
and ![]() that describe the best fit are
that describe the best fit are ![]() and
and ![]() . Therefore, the best-fit model is:
. Therefore, the best-fit model is:
![]()
The following is the Mathematica code used along with the output
View Mathematica Code
Data = {{0.0001, 204.18}, {0.0003, 226.4}, {0.0015, 270.35}, {0.0025, 276.86}, {0.004, 296.86}, {0.005, 299.3}, {0.015, 334.65}, {0.025,346.56}, {0.04, 371.81}, {0.05, 377.45}, {0.1, 398.01}, {0.15, 422.45}, {0.2, 434.42}};
model = NonlinearModelFit[Data, Kk*eps^(n), {Kk, n}, eps]
y = Normal[model]
Print["R^2=",R2 = model["RSquared"]]
Plot[y, {eps, 0, 0.21}, Epilog -> {PointSize[Large], Point[Data]}, PlotLegends -> {"Model"}, AxesLabel -> {"Eps_p", "Sigma_y"}, AxesOrigin -> {0, 0}]
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
Data = [[0.0001, 204.18], [0.0003, 226.4], [0.0015, 270.35], [0.0025, 276.86], [0.004, 296.86], [0.005, 299.3], [0.015, 334.65], [0.025,346.56], [0.04, 371.81], [0.05, 377.45], [0.1, 398.01], [0.15, 422.45], [0.2, 434.42]]
def f(eps, k, n): return k*eps**n
coeff, covariance = curve_fit(f, [point[0] for point in Data],
[point[1] for point in Data])
print("coeff: ",coeff)
x_val = np.arange(0,0.21,0.001)
plt.title('%.5feps**(%.5f)' % tuple(coeff))
plt.plot(x_val, f(x_val, coeff[0], coeff[1]))
plt.scatter([point[0] for point in Data], [point[1] for point in Data], c='k')
plt.xlabel("Eps_p"); plt.ylabel("Sigma_y")
plt.grid(); plt.show()
# R squared
x = np.array([point[0] for point in Data])
y = np.array([point[1] for point in Data])
y_fit = f(x, coeff[0], coeff[1])
ss_res = np.sum((y - y_fit)**2)
ss_tot = np.sum((y - np.mean(y))**2)
r2 = 1 - (ss_res / ss_tot)
print("R Squared: ",r2)

The following links provide the MATLAB codes for implementing a nonlinear model fit for yield strength vs plastic strain. The function for the model is provided in File 2.
Example 2
Exponential and Logarithmic Models offer a wide range of model functions that can be used for various engineering applications. An example is the exponential model that describes an initial rapid increase in the dependent variable ![]() which then levels off to become asymptotic to an upper limit
which then levels off to become asymptotic to an upper limit ![]() :
:
![]()
where ![]() and
and ![]() are the model parameters. For plastic materials, Armstrong and Frederick proposed this model in 1966 (republished here in 2007) to describe how a quantity called the “Centre of the Yield Surface” changes with the increase in the plastic strain. If
are the model parameters. For plastic materials, Armstrong and Frederick proposed this model in 1966 (republished here in 2007) to describe how a quantity called the “Centre of the Yield Surface” changes with the increase in the plastic strain. If ![]() is the centre of the yield surface and
is the centre of the yield surface and ![]() is the plastic strain, then, the model for
is the plastic strain, then, the model for ![]() has the form:
has the form:
![]()
Find the values of ![]() and
and ![]() for the best fit to the experimental data
for the best fit to the experimental data ![]() given by: (0.0001,2.067),(0.005,3.96),(0.0075,6.22),(0.008,8.07),(0.009,9.32),(0.01,12.02),(0.02,13.2),(0.03,15.22),(0.04,15.51),(0.05,15.44),(0.06,15.1),(0.075,15.76),(0.1,15.11),(0.17,15.53),(0.2,15.26)
given by: (0.0001,2.067),(0.005,3.96),(0.0075,6.22),(0.008,8.07),(0.009,9.32),(0.01,12.02),(0.02,13.2),(0.03,15.22),(0.04,15.51),(0.05,15.44),(0.06,15.1),(0.075,15.76),(0.1,15.11),(0.17,15.53),(0.2,15.26)
Solution
Unlike the model in the previous question, this model cannot be linearized. The NonlinearModelFit built-in function in Mathematica will be used. The array of data is input as a list in the variable Data. The NonlinearModelFit function is then used and the output is stored in the variable: “model”. The form of the best fit function is evaluated using the built-in function Normal[model]. ![]() can be evaluated as well as shown in the code below. The values of
can be evaluated as well as shown in the code below. The values of ![]() and
and ![]() that describe the best fit are
that describe the best fit are ![]() and
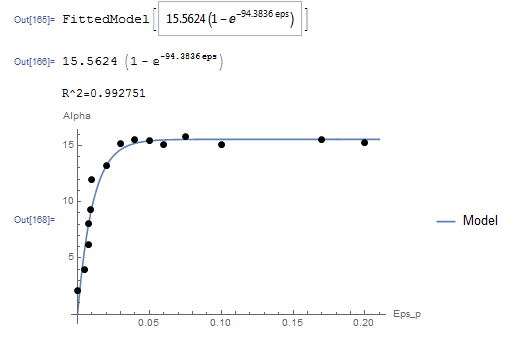
and ![]() . Therefore, the best-fit model is:
. Therefore, the best-fit model is:
![]()
The following is the Mathematica code used along with the output View Mathematica Code
Data = {{0.0001, 2.067}, {0.005, 3.96}, {0.0075, 6.22}, {0.008,8.07}, {0.009, 9.32}, {0.01, 12.02}, {0.02, 13.2}, {0.03,15.22}, {0.04, 15.51}, {0.05, 15.44}, {0.06, 15.1}, {0.075,15.76}, {0.1, 15.11}, {0.17, 15.53}, {0.2, 15.26}};
model = NonlinearModelFit[Data, Cc (1 - E^(-gamma*eps)), {Cc, gamma}, eps]
y = Normal[model]
Print["R^2=", R2 = model["RSquared"]]
Plot[y, {eps, 0, 0.21}, Epilog -> {PointSize[Large], Point[Data]}, PlotLegends -> {"Model"}, AxesLabel -> {"Eps_p", "Alpha"}, AxesOrigin -> {0, 0}]
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
Data = [[0.0001, 2.067], [0.005, 3.96], [0.0075, 6.22], [0.008,8.07], [0.009, 9.32], [0.01, 12.02], [0.02, 13.2], [0.03,15.22], [0.04, 15.51], [0.05, 15.44], [0.06, 15.1], [0.075,15.76], [0.1, 15.11], [0.17, 15.53], [0.2, 15.26]]
def f(eps, c, gamma): return c*(1 - np.exp(-gamma*eps))
coeff, covariance = curve_fit(f, [point[0] for point in Data],
[point[1] for point in Data])
print("coeff: ",coeff)
x_val = np.arange(0,0.21,0.001)
plt.title('%.5f(1 - e**(-%.5feps))' % tuple(coeff))
plt.plot(x_val, f(x_val, coeff[0], coeff[1]))
plt.scatter([point[0] for point in Data], [point[1] for point in Data], c='k')
plt.xlabel("Eps_p"); plt.ylabel("Alpha")
plt.grid(); plt.show()
# R squared
x = np.array([point[0] for point in Data])
y = np.array([point[1] for point in Data])
y_fit = f(x, coeff[0], coeff[1])
ss_res = np.sum((y - y_fit)**2)
ss_tot = np.sum((y - np.mean(y))**2)
r2 = 1 - (ss_res / ss_tot)
print("R Squared: ",r2)
The following links provide the MATLAB codes for implementing a Nonlinear model fit for centre of the yield surface. The function for the model is provided in File 2.
