Engineering at Alberta Courses

Mathematica Lab Tutorials: Lab 11

Consider the following BVP

$4y'' (x)-2y(x)-x=0$

With the boundary conditions $y(0)=0$ and $y(6)=0$

Find the exact solution using the built-in DSolve function in Mathematica.
Use the finite difference method with n=5 intervals to find a numerical solution.
Plot the exact solution overlapping the data points obtained using the numerical solution.
Find the maximum absolute error.
Write a procedure whose input is $n$ and the output is the maximum absolute error.
Plot the curve of the maximum absolute error vs. $n$ for $n=4,5,6,7,8,\cdots,30$
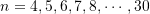
Plot the curve of the maximum absolute error vs. 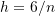$h=6/n$ for $n=8,16,32,64,128,256$
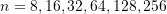
Fit the nonlinear model 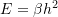$E=\beta h^2$ to the data of maximum error vs. 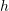$h$ (Note the error is expected to be 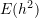$E(h^2)$ because the basic formula for the centred finite difference scheme is used)