Engineering at Alberta Courses » (Explicit) Euler Method

Solution Methods for IVPs: (Explicit) Euler Method

(Explicit) Euler Method

The Euler method is one of the simplest methods for solving first-order IVPs. Consider the following IVP:

$\frac{\mathrm{d}x}{\mathrm{d}t}=F(x,t)$

Assuming that the value of the dependent variable $x$ (say $x_i$ ) is known at an initial value $t_i$ , then, we can use a Taylor approximation to estimate the value of $x$ at $t=t_{i+1}$ , namely $x(t_{i+1})$ with $h=t_{i+1}-t_i$ :

$x(t_{i+1})=x_i+\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{t_i} (h) +\mathcal{O}(h^2)$

Substituting the differential equation into the above equation yields:

$x(t_{i+1})=x_i+F(x_i,t_i) (h) +\mathcal{O}(h^2)$

Therefore, as an approximation, an estimate for $x(t_{i+1})$ can be taken as $x_{i+1}$ as follows:

$x(t_{i+1})\approx x_{i+1}=x_i+F(x_i,t_i) (h)$

Using this estimate, the local truncation error is thus proportional to the square of the step size with the constant of proportionality related to the second derivative of $x$ , which is the first derivative of the given IVP:

$E_{\mbox{local}}=\mathcal{O}(h^2)$

If the errors from each interval are added together, with $n=\frac{L}{h}$ being the number of intervals and $L$ the total length $t_n-t_0$ , then, the total error is:

$E=\mathcal{O}(h^2) \frac{L}{h}=\mathcal{O}(h)$

There are many examples in engineering and biology in which such IVPs appear. Check this page for examples.

The following Mathematica code provides a procedure whose inputs are

The differential equation as a function of the dependent variable $x$ and the independent variable 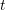$t$ .
The step size $h$ .
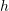The initial value 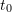$t_0$ and the final value $t_{max}$ of the independent variable.
The initial value $x(t_0)=x_0$ .

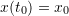The procedure then carries on the Euler method and outputs the required data vector.

View Mathematica Code

EulerMethod[fp_, x0_, h_, t0_, tmax_] :=
 (n = (tmax - t0)/h + 1;
  xtable = Table[0, {i, 1, n}];
  xtable[[1]] = x0;
  Do[xtable[[i]] = xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h], {i, 2,  n}];
  Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
  Data)
function1[y_, t_] := 0.05 y
function2[x_, t_] := 0.015 x
EulerMethod[function1, 35, 1.0, 0, 50] // MatrixForm
EulerMethod[function2, 35, 1.0, 0, 50] // MatrixForm

View Python Code

def EulerMethod(fp, x0, h, t0, tmax):
  n = int((tmax - t0)/h + 1)
  xtable = [0 for i in range(n)]
  xtable[0] = x0
  for i in range(1,n):
    xtable[i] = xtable[i - 1] + h*fp(xtable[i - 1], t0 + (i - 1)*h)
  Data = [[t0 + i*h, xtable[i]] for i in range(n)]
  return Data
def function1(y, t): return 0.05*y
def function2(x, t): return 0.015*x
display(EulerMethod(function1, 35, 1.0, 0, 50))
display(EulerMethod(function2, 35, 1.0, 0, 50))

Example 1

The Canadian population at $t=0$ (current year) is 35 million. If 2.5% of the population have a child in a given year, while the death rate is 1% of the population, what will the population be in 50 years? What if 6% of the population have a child in a given year and the death rate is kept constant at 1%, what will the population be in 50 years?

Solution

The rate of growth is directly proportional to the current population with the constant of proportionality $k=0.025-0.01=0.015$ . If $x$ represents the population in millions and $t$ represents the time in years, then the IVP is given by:

$\frac{\mathrm{d}x}{\mathrm{d}t}=0.015 x$

With the initial condition of $x(0)=35$ , the exact solution to this differential equation is:

$x=35e^{0.015t}$

If the birth rate is 6%, then $k=0.06-0.01=0.05$ and the exact solution of the population follows the following equation:

$x=35e^{0.05t}$

The Euler method provides a numerical solution as follows. Using a step size of $h=t_{i+1}-t_i=1$ , we can set $t_0=0, t_1=1, t_2=2, \cdots, t_{50}=50$ years. The value of $x_0$ is given as 35 million. When $k=0.015$ , the value of $x_1$ in millions is given by:

$x_1=x_0+h\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{x=x_0,t=t_0}=35+0.015\times 35=35.525$

The value of $x_2$ is given by:

$x_2=x_1+h\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{x=x_1,t=t_1}=35.525+0.015\times 35.525=36.0579$

Iterating further, the values of $x$ at each time point can be obtained. The following is the Microsoft Excel table showing the values of $t_i$ in years and the corresponding values of the population $x_i$ in millions:
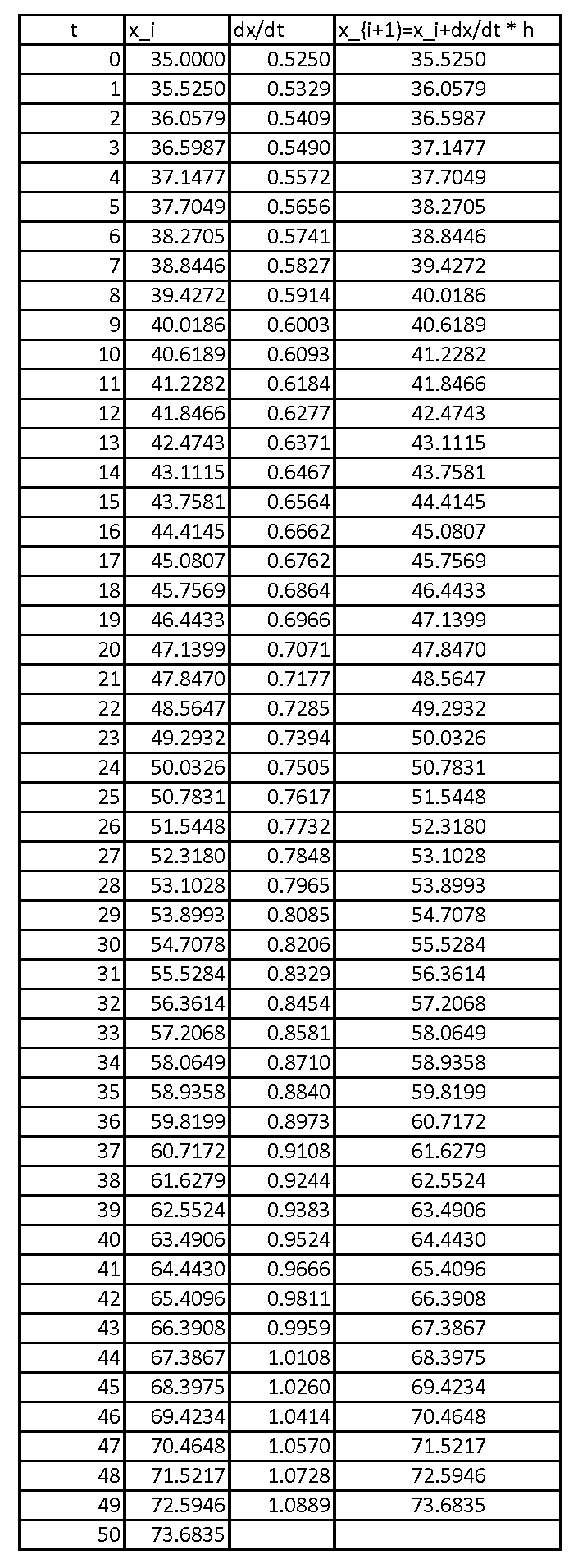
IVPe1

When $k=0.015$ , the numerical procedure produces a very good approximation for the population at $t=50$ years. The error between the prediction of the exact solution to the differential equation and the numerical value at $t=50$ is given in millions by:

$E=35e^{(0.015\times 50)} - 73.6835=74.095-73.6835=0.4$

The relative error in this case is given by:

$E_r=\frac{0.4}{74.095}=0.005$

For the second case, when $k=0.05$ , the value of $x_1$ in millions is given by:

$x_1=x_0+h\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{x=x_0,t=t_0}=35+0.05\times 35=36.75$

Proceeding iteratively, the following is the Microsoft Excel table showing the values of $t_i$ in years and the corresponding values of the population $x_i$ in millions:
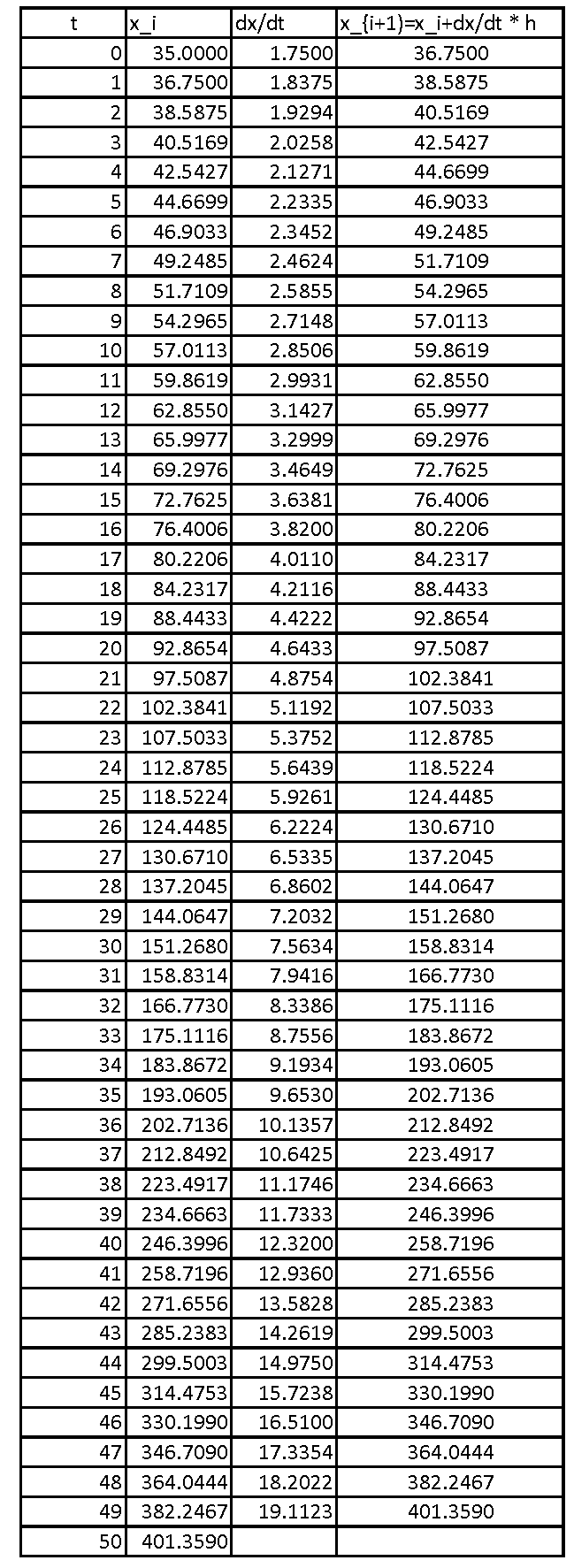
IVPe2

Compared to the previous case, when $k=0.05$ , the numerical procedure is not as good. The error between the prediction of the exact solution to the differential equation and the numerical value at $t=50$ is given in millions by:

$E=35e^{(0.05\times 50)} - 401.359=426.387-401.359=25.0283$

The relative error in this case is given by:

$E_r=\frac{25.0283}{426.387}=0.06$

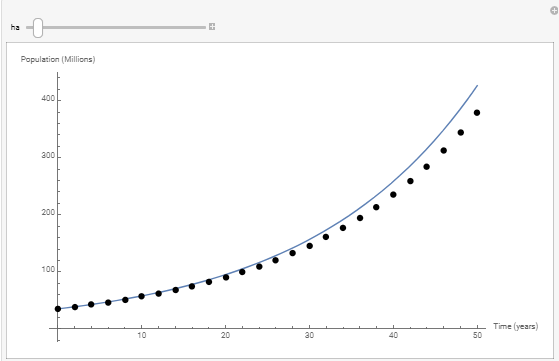
The following is the graph showing the exact solution versus the data using the Euler method for both cases. The Mathematica code used is given below. Notice how the error in the Euler method increases as $t$ increases.
IVP2

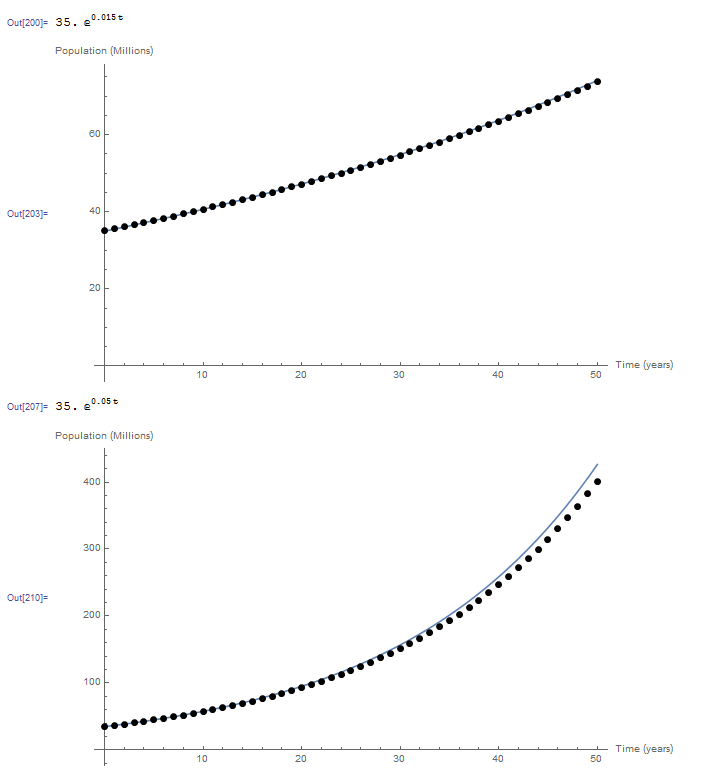View Mathematica Code

EulerMethod[fp_, x0_, h_, t0_, tmax_] := 
  (n = (tmax - t0)/h + 1;
  xtable = Table[0, {i, 1, n}];
  xtable[[1]] = x0;
  Do[xtable[[i]] =  xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h], {i, 2, n}];
  Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
  Data)

Clear[x, xtable]
k = 0.015;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := k*x;
Data = EulerMethod[fp, 35, 1.0, 0, 50];
Plot[x, {t, 0, 50}, Epilog -> {PointSize[Large], Point[Data]}, AxesOrigin -> {0, 0}, AxesLabel -> {"Time (years)", "Population (Millions)"}]

Clear[x, xtable]
k = 0.05;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := k*x;
Data = EulerMethod[fp, 35, 1.0, 0, 50];
Plot[x, {t, 0, 50}, Epilog -> {PointSize[Large], Point[Data]}, AxesOrigin -> {0, 0}, AxesLabel -> {"Time (years)", "Population (Millions)"}]

View Python Code

# UPGRADE: need Sympy 1.2 or later, upgrade by running: "!pip install sympy --upgrade" in a code cell
# !pip install sympy --upgrade
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
sp.init_printing(use_latex=True)

def EulerMethod(fp, x0, h, t0, tmax):
  n = int((tmax - t0)/h + 1)
  xtable = [0 for i in range(n)]
  xtable[0] = x0
  for i in range(1,n):
    xtable[i] = xtable[i - 1] + h*fp(xtable[i - 1], t0 + (i - 1)*h)
  Data = [[t0 + i*h, xtable[i]] for i in range(n)]
  return Data

x = sp.Function('x')
t = sp.symbols('t')
k = 0.015
sol = sp.dsolve(x(t).diff(t) - k*x(t), ics={x(0): 35})
display(sol)
def fp(x, t): return k*x
Data = EulerMethod(fp, 35, 1.0, 0, 50)
x_val = np.arange(0,50,0.1)
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.scatter([point[0] for point in Data],[point[1] for point in Data])
plt.xlabel("Time (years)"); plt.ylabel("Population (Millions)")
plt.grid(); plt.show()

k = 0.05
sol = sp.dsolve(x(t).diff(t) - k*x(t), ics={x(0): 35})
display(sol)
Data = EulerMethod(fp, 35, 1.0, 0, 50)
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.scatter([point[0] for point in Data],[point[1] for point in Data])
plt.xlabel("Time (years)"); plt.ylabel("Population (Millions)")
plt.grid(); plt.show()

MATLAB files: File 1 (ex12_1.m) File 2 (explicit_euler.m)

The following tool illustrates the effect of choosing the step size $h$ on the difference between the numerical solution (shown as dots) and the exact solution (shown as the blue curve) for the case when $k=0.05$ . The smaller the step size, the more accurate the solution is. The higher the value of $h$ , the more the numerical solution deviates from the exact solution. The error increases away from the initial conditions.

Example 2

This example is adopted from this page. A lake of volume $10,000 m^3$ has an initial concentration of a particular pollutant of $5$ parts per billion (ppb). This pollutant is due to a pesticide that is no longer available in the market. The volume of the lake is constant throughout the year, with daily water flowing into and out of the lake at the rate of $q=100+50\cos{(2\pi t/365)} \frac{m^3}{day}$ . As the pesticide is no longer used, the concentration of the pollutant in the surrounding soil is given in ppb as a function of $t$ (days) by $c_{in}=5e^{\left(\frac{-2t}{1000}\right)}$ which indicates that the concentration is following an exponential decay. This concentration can be assumed to be that of the pollutant in the fluid flowing into the lake. The concentration of the pollutant in the fluid flowing out of the lake is the same as the concentration in the lake. What is the concentration of this particular pollutant in the lake after two years?

Solution

The first step in this problem is to properly write the differential equation that needs to be solved. If $\alpha$ is the total amount of pollutant in the lake, then, the rate of change of $\alpha$ with respect to $t$ is equal to the total amount of pollutant entering into the lake per day. Each day, the total amount of pollutant entering the lake is given by $c_{in}\times q$ , while the total amount of pollutant exiting the lake is given by $c\times q$ , where $c$ is the concentration of the pollutant in the lake. Therefore:

$\frac{\mathrm{d}\alpha}{\mathrm{d}t}=\left(100+50\cos{(2\pi t/365)}\right)\left(c_{in}-c\right)$

The concentration is equal to the total amount divided by the volume of the lake, therefore, the differential equation in terms of $c$ is given by:

$\frac{\mathrm{d}c}{\mathrm{d}t}=\frac{\left(100+50\cos{(2\pi t/365)}\right)}{10000}\left(c_{in}-c\right)=\frac{\left(100+50\cos{(2\pi t/365)}\right)}{10000}\left(5e^{\left(\frac{-2t}{1000}\right)}-c\right)$

Notice that finding an exact solution to the above differential equation is not an easy task and a numerical solution would be the preferred solution in this case. Taking $h=t_{i+1}-t_i=1$ day, $t_0=0$ , and $c_0=5$ ppb the Euler method can be used to find the concentration $c$ at $t=730$ days. You can download the Microsoft Excel file example2.xlsx showing the calculations and the produced graph.
Taking $h=1$ day, we will show the calculations for the estimates $c_1$ and $c_2$ . At $t_1=1$ day:

$\begin{split}c_1&=c_0+h\frac{\mathrm{d}c}{\mathrm{d}t}\bigg|_{c=c_0,t=t_0}\\&=5+1\left(\frac{\left(100+50\cos{(2\pi 0/365)}\right)}{10000}\left(5e^{\left(\frac{-2(0)}{1000}\right)}-5\right)\right)\\&=5\end{split}$

At $t_2=2$ days:

$\begin{split}c_2&=c_1+h\frac{\mathrm{d}c}{\mathrm{d}t}\bigg|_{c=c_1,t=t_1}\\&=5+1\left(\frac{\left(100+50\cos{(2\pi 1/365)}\right)}{10000}\left(5e^{\left(\frac{-2(1)}{1000}\right)}-5\right)\right)\\&=4.9999\end{split}$

Carrying on produces the values of $c$ at the remaining time intervals up to $t=2(365)$ days. The following is the output produced by the Mathematica code below.
IPV1

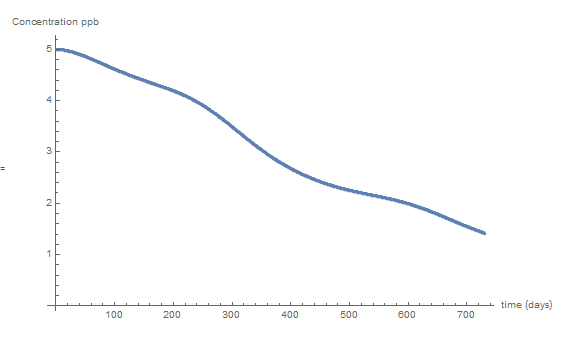View Mathematica Code

EulerMethod[fp_, x0_, h_, t0_, tmax_] :=
 (n = (tmax - t0)/h + 1;
  xtable = Table[0, {i, 1, n}];
  xtable[[1]] = x0;
  Do[xtable[[i]] =  xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h], {i, 2, n}];
  Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
  Data)
f[t_] := 100 + 50*Cos[2 Pi*t/365];
cin[t_] := 5 E^(-2 t/1000);
fp[c_, t_] := f[t] (cin[t] - c)/10000;
Data = EulerMethod[fp, 5, 1.0, 0, 365*2];
ListPlot[Data, AxesLabel -> {"time (days)", "Concentration ppb"}]

View Python Code

import numpy as np
import matplotlib.pyplot as plt

def EulerMethod(fp, x0, h, t0, tmax):
  n = int((tmax - t0)/h + 1)
  xtable = [0 for i in range(n)]
  xtable[0] = x0
  for i in range(1,n):
    xtable[i] = xtable[i - 1] + h*fp(xtable[i - 1], t0 + (i - 1)*h)
  Data = [[t0 + i*h, xtable[i]] for i in range(n)]
  return Data
def f(t): return 100 + 50*np.cos(2*np.pi*t/365)
def cin(t): return 5*np.exp(-2*t/1000)
def fp(c, t): return f(t)*(cin(t) - c)/10000
Data = EulerMethod(fp, 5, 1.0, 0, 365*2)
plt.scatter([point[0] for point in Data],[point[1] for point in Data])
plt.xlabel("Time (days)"); plt.ylabel("Concentration ppb")
plt.grid(); plt.show()

MATLAB files: File 1 (ex12_2.m) File 2 (explicit_euler.m)

Example 3

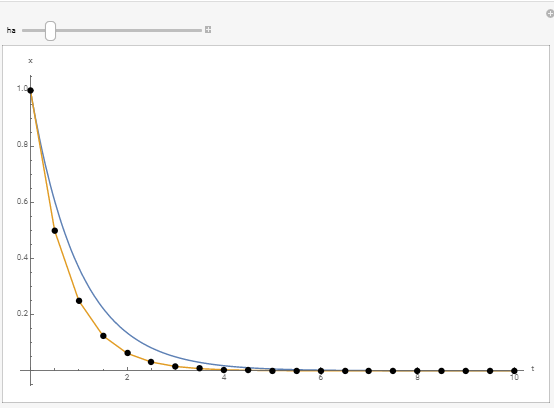
In this example we investigate the issue of stability of numerical solution of differential equations using the Euler method. Consider the IVP of the form:

$\frac{\mathrm{d}x}{\mathrm{d}t}=-x$

If $x_0=1$ , compare the two solutions taking a step size of $h=0.1$ , and a step size of $h=3$ .

Solution

The exact solution to the given equation is given by:

$x=e^{-t}$

Using an explicit Euler scheme, the value of $x_{i+1}$ can be obtained as follows:

$x_{i+1}=x_i+h\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{x_i}=(1-h)x_i=(1-h)(1-h)x_{i-1}$

Therefore:

$x_{i+1}=(1-h)^{i+1}x_0$

When $h=0.1$ , the term $(1-h)^{i+1}=0.9^{i+1}$ is bounded for any value of $i$ which means that the value of $x_{i+1}$ is always bounded. However, if $h=3$ , then, the term $(1-h)^{i+1}=(-2)^{i+1}$ oscillates wildly leading to an instability in the numerical scheme!
The following tool illustrates the difference between the obtained result for $t\in[0,10]$ . Vary the value of $h$ and try to identify the point above which the obtained solution (black dots) starts oscillating wildly around the exact solution (blue curve).

Open Educational Resources

Solution Methods for IVPs: (Explicit) Euler Method

(Explicit) Euler Method

Example 1

Solution

Example 2

Solution

Example 3

Solution

Lecture Video

Leave a Reply Cancel reply