Direct Methods: Naive Gauss Elimination
The Method
The naive Gauss elimination is a procedure in which the linear system of equations is manipulated such that the coefficients of the component ![]() are eliminated from equation
are eliminated from equation ![]() to equation
to equation ![]() . It would then be possible to solve for
. It would then be possible to solve for ![]() using the last equation, and then backward substitute to find the remaining components. The procedure is divided into two steps, forward elimination followed by backward substitution. We will illustrate the process in the following example. Consider the system of equations
using the last equation, and then backward substitute to find the remaining components. The procedure is divided into two steps, forward elimination followed by backward substitution. We will illustrate the process in the following example. Consider the system of equations ![]() defined as:
defined as:
![Rendered by QuickLaTeX.com \[\begin{split} 2x_1+2x_2+2x_3&=6\\ 2x_1+3x_2+4x_3&=4\\ -x_1+2x_2+3x_3&=8\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e0c6bc7acc24184d6721a7da375fc308_l3.png)
Forward elimination: First, we will use the first equation to eliminate the coefficients of ![]() in equation 2 and 3. By multiplying the first equation by -1 and adding it to the second equation we get:
in equation 2 and 3. By multiplying the first equation by -1 and adding it to the second equation we get:
![Rendered by QuickLaTeX.com \[\begin{split} 2x_1+2x_2+2x_3&=6\\ (2-2)x_1+(3-2)x_2+(4-2)x_3&=(4-6)\\ -x_1+2x_2+3x_3&=8\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6f624f6ec9842d4ff5552d0881d1b957_l3.png)
which becomes:
![Rendered by QuickLaTeX.com \[\begin{split} 2x_1+2x_2+2x_3&=6\\ 0+1x_2+2x_3&=-2\\ -x_1+2x_2+3x_3&=8\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a9fcd5b41c83d0a5dc78b6e378e0daf5_l3.png)
By multiplying the first equation by ![]() and adding it to the third equation we get:
and adding it to the third equation we get:
![Rendered by QuickLaTeX.com \[\begin{split} 2x_1+2x_2+2x_3&=6\\ 0+1x_2+2x_3&=-2\\ 0+3x_2+4x_3&=11\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ce00ad9e7f1f89e30fedc23d485ad790_l3.png)
We are now ready to eliminate the coefficient of ![]() from equation 3 by multiplying equation 2 by -3 and adding it to equation 3:
from equation 3 by multiplying equation 2 by -3 and adding it to equation 3:
![Rendered by QuickLaTeX.com \[\begin{split} 2x_1+2x_2+2x_3&=6\\ 0+1x_2+2x_3&=-2\\ 0+0-2x_3&=17\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a43e5cf864220463131200c08ad1e29d_l3.png)
Backward substitution: Solving the above system becomes very simple. ![]() is straightforward, it is equal to
is straightforward, it is equal to ![]() .
. ![]() can be obtained from the second equation as:
can be obtained from the second equation as: ![]() and finally
and finally ![]() . Therefore, the solution is:
. Therefore, the solution is:
![Rendered by QuickLaTeX.com \[ x=\left(\begin{array}{c}-3.5\\15\\-8.5\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-29b2a8fb6a85bebbcd86984256f2db00_l3.png)
Of course, as expected, if we multiply the original ![]() by
by ![]() we should get the matrix
we should get the matrix ![]() .
.
The Naive Gauss elimination method can be implemented in matrix form of dimensions ![]() as follows:
as follows:
![Rendered by QuickLaTeX.com \[ \left(\begin{array}{ccc|c}2&2&2&6\\2&3&4&4\\-1&2&3&8\end{array}\right)\Rightarrow \left(\begin{array}{ccc|c}2&2&2&6\\0&1&2&-2\\-1&2&3&8\end{array}\right) \Rightarrow \left(\begin{array}{ccc|c}2&2&2&6\\0&1&2&-2\\0&3&4&11\end{array}\right) \Rightarrow \left(\begin{array}{ccc|c}2&2&2&6\\0&1&2&-2\\0&0&-2&17\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0748352b12f949c2f09015d9a2bf095f_l3.png)
The following code implements the above calculations in Mathematica
View Mathematica CodeA = {{2, 2, 2}, {2, 3, 4}, {-1, 2, 3}};
b = {6, 4, 8};
Aa = {{2, 2, 2, b[[1]]}, {2, 3, 4, b[[2]]}, {-1, 2, 3, b[[3]]}};
Aa[[2]] = Aa[[2]] + -1*Aa[[1]]
Aa[[3]] = Aa[[3]] + 1/2*Aa[[1]]
Aa[[3]] = Aa[[3]] - 3 Aa[[2]]
Aa // MatrixForm
x3 = Aa[[3, 4]]/Aa[[3, 3]]
x2 = (Aa[[2, 4]] - Aa[[2, 3]]*x3)/Aa[[2, 2]]
x1 = (Aa[[1, 4]] - Aa[[1, 2]]*x2 - Aa[[1, 3]]*x3)/Aa[[1, 1]]
import numpy as np
A = [[2, 2, 2], [2, 3, 4], [-1, 2, 3]]
b = [6, 4, 8]
Aa = np.array([[2, 2, 2, b[0]], [2, 3, 4, b[1]], [-1, 2, 3, b[2]]])
Aa[1] = Aa[1] + -1*Aa[0]
print("Aa[1]:",Aa[1])
Aa[2] = Aa[2] + 1/2*Aa[0]
print("Aa[2]:",Aa[2])
Aa[2] = Aa[2] - 3*Aa[1]
print("Aa[2]:",Aa[2])
print("Aa:",Aa)
x3 = Aa[2, 3]/Aa[2, 2]
print("x3:",x3)
x2 = (Aa[1, 3] - Aa[1, 2]*x3)/Aa[1, 1]
print("x2:",x2)
x1 = (Aa[0, 3] - Aa[0, 1]*x2 - Aa[0, 2]*x3)/Aa[0, 0]
print("x1:",x1)
Programming the Method
The following are the steps to program the Naive Gauss Elimination method. Assuming an ![]() number of equations in
number of equations in ![]() unknowns of the form
unknowns of the form ![]() :
:
- Form the combined matrix
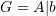
- Forward elimination: Use the pivot elements
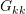 on the row
on the row  as “Pivot” elements. Use the “Pivot” elements to eliminate the components
as “Pivot” elements. Use the “Pivot” elements to eliminate the components 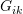 with
with  from
from 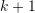 to
to  . This is done by iterating
. This is done by iterating  from
from 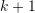 to
to  and for each row
and for each row  , doing the operation
, doing the operation  .
. - Backward substitution: The element
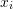 with
with  running backwards from
running backwards from  to 1 can be found using the equation:
to 1 can be found using the equation:
![Rendered by QuickLaTeX.com \[ x_i=\frac{G_{i(n+1)}-\sum_{l=i+1}^nG_{il}x_l}{G_{ii}} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-42ff4dd903d9b2b1310d57b34def779b_l3.png)
The following is the code that relies on the “Sum” built-in function in Mathematica.
View Mathematica Code(*Procedure*)
GaussElimination[A_, b_] :=
(n = Length[A];
G = Transpose[Insert[Transpose[A], b, n + 1]];
For[k = 1, k <= n, k++,
Do[G[[i]] = G[[i]] - G[[i, k]]/G[[k, k]]*G[[k]], {i, k + 1, n}]];
x = Table[0, {i, 1, n}];
For[i = n, i >= 1, i = i - 1,
x[[i]] = (G[[i, n + 1]] - Sum[G[[i, l]]*x[[l]], {l, i + 1, n}])/G[[i, i]]];
x)
(*An example*)
A = {{1, 2, 3, 5}, {2, 0, 1, 4}, {1, 2, 2, 5}, {4, 3, 2, 2}};
b = {-4, 8, 0, 10};
(*Applying the procedure to the example*)
N[GaussElimination[A, b]]
GaussElimination[A, b]
import numpy as np
# Procedure
def GaussElimination(A,b):
n = len(A)
G = (np.vstack([A.astype(np.float).T, b.astype(np.float)])).T
for k in range(n):
for i in range(k + 1, n):
G[i] = G[i] - G[i][k]/G[k][k]*G[k]
x = np.zeros(n)
for i in range(n-1,-1,-1):
x[i] = (G[i][n] - sum([G[i][l]*x[l] for l in range(i + 1, n)]))/G[i][i]
return x
# An example
A = np.array([[1, 2, 3, 5], [2, 0, 1, 4], [1, 2, 2, 5], [4, 3, 2, 2]])
b = np.array([-4, 8, 0, 10])
# Applying the procedure to the example
GaussElimination(A, b)
The following is the code that does not rely on the built-in function in Mathematica.
View Mathematica Code(*Procedure*)
GaussElimination[A_, b_] := (n = Length[A];
G = Transpose[Insert[Transpose[A], b, n + 1]];
For[k = 1, k <= n, k++,
Do[G[[i]] = G[[i]] - G[[i, k]]/G[[k, k]]*G[[k]], {i, k + 1, n}]];
x = Table[0, {i, 1, n}];
For[i = n, i >= 1,
i = i - 1, (BB = 0; Do[BB = G[[i, l]]*x[[l]] + BB, {l, i + 1, n}];
x[[i]] = (G[[i, n + 1]] - BB)/G[[i, i]])];
x)
(*An example*)
A = {{1, 2, 3, 5}, {2, 0, 1, 4}, {1, 2, 2, 5}, {4, 3, 2, 2}};
b = {-4, 8, 0, 10};
(*Applying the procedure to the example*)
N[GaussElimination[A, b]]
GaussElimination[A, b]
import numpy as np
# Procedure
def GaussElimination(A,b):
n = len(A)
G = (np.vstack([A.astype(np.float).T, b.astype(np.float)])).T
for k in range(n):
for i in range(k + 1, n):
G[i] = G[i] - G[i][k]/G[k][k]*G[k]
x = np.zeros(n)
for i in range(n-1,-1,-1):
BB = 0
for l in range(i+1, n):
BB = G[i][l]*x[l] + BB
x[i] = (G[i][n] - BB)/G[i][i]
return x
# An example
A = np.array([[1, 2, 3, 5], [2, 0, 1, 4], [1, 2, 2, 5], [4, 3, 2, 2]])
b = np.array([-4, 8, 0, 10])
# Applying the procedure to the example
GaussElimination(A, b)
The following link provides the MATLAB code for implementing the Naive Gauss Elimination Method.
Why Naive
The method described above is considered “naive” for two reasons. The first reason is that it fails to find a solution if a pivot element (one of the diagonal elements) is found to be zero. For example, consider the linear system:
![Rendered by QuickLaTeX.com \[ \left(\begin{matrix}1&0&0\\0&0&1\\0&1&0\end{matrix}\right)\left(\begin{matrix}x_1\\x_2\\x_3\end{matrix}\right)=\left(\begin{matrix}1\\1\\1\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0d383565189f024d2edc9dbf8973da09_l3.png)
This is really simple and the solution is just ![]() . However, the code fails to find a solution because when the second row is used for elimination, the pivot element
. However, the code fails to find a solution because when the second row is used for elimination, the pivot element ![]() is equal to zero, and so, an error is encountered. Try the above systems out and see the error that Mathematica spits out. This problem can be solved by simply exchanging rows 2 and 3. The same issue will be encountered for the following system:
is equal to zero, and so, an error is encountered. Try the above systems out and see the error that Mathematica spits out. This problem can be solved by simply exchanging rows 2 and 3. The same issue will be encountered for the following system:
![Rendered by QuickLaTeX.com \[ \left(\begin{matrix}1&1&0\\0&0&1\\1&0&0\end{matrix}\right)\left(\begin{matrix}x_1\\x_2\\x_3\end{matrix}\right)=\left(\begin{matrix}1\\1\\1\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9f4007af5dbd4699a7c909676be98b65_l3.png)
In this case, one solution would be to rearrange the equations such that equation 3 would be equation 1. In general, the naive Gauss elimination code presented above can be augmented so that the pivot elements are chosen to be the largest elements in the column below. This augmentation is termed: “Partial Pivoting”. Partial Pivoting is performed by exchanging the rows. In this case, the order of the variables ![]() stays the same. In rare cases, there could be a need to exchange the columns as well; a procedure termed “Complete Pivoting”, but this adds the complication of re-arranging the variables.
stays the same. In rare cases, there could be a need to exchange the columns as well; a procedure termed “Complete Pivoting”, but this adds the complication of re-arranging the variables.
The second reason why it is called naive is that the method essentially produces an upper triangular matrix that can be easily solved. It is important to note that if the system is already a lower triangular matrix, then there is no need to employ the forward elimination procedure, because we can simply use forward substitution to find ![]() in this order.
in this order.
Consider the following system:
![Rendered by QuickLaTeX.com \[ \left(\begin{matrix}1&0&0\\1&1&0\\1&1&1\end{matrix}\right)\left(\begin{matrix}x_1\\x_2\\x_3\end{matrix}\right)=\left(\begin{matrix}1\\0\\1\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-75ec75ca5ace172c73a2e39d9d872012_l3.png)
It is straightforward that ![]() ,
, ![]() , and
, and ![]() . However, employing the naive Gauss elimination would conduct the following steps:
. However, employing the naive Gauss elimination would conduct the following steps:
![Rendered by QuickLaTeX.com \[ \left(\begin{array}{ccc|c}1&0&0&1\\1&1&0&0\\1&1&1&1\end{array}\right)\Rightarrow \left(\begin{array}{ccc|c}1&0&0&1\\0&1&0&-1\\1&1&1&1\end{array}\right) \Rightarrow \left(\begin{array}{ccc|c}1&0&0&1\\0&1&0&-1\\0&1&1&0\end{array}\right) \Rightarrow \left(\begin{array}{ccc|c}1&0&0&1\\0&1&0&-1\\0&0&1&1\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b23d3d487ef40a97a11f74006fa55c85_l3.png)
