Python Lab Tutorials: Lab 2
- Consider the relationship
![Rendered by QuickLaTeX.com \[y=\sin{\frac{\pi x}{6}}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f523d4e1b33fe8a7b0e07c55ffb365cf_l3.png)
Using Sympy, find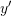 and
and 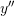 . Evaluate
. Evaluate 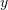 ,
, 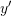 , and
, and 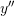 at
at  . Then, using Matplotlib, plot the relationships
. Then, using Matplotlib, plot the relationships 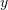 ,
, 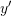 , and
, and 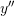 for the domain
for the domain ![Rendered by QuickLaTeX.com x\in[-5,5]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-578dd5c0f0c4f35b8dd518ad9b002eff_l3.png) by first finding the y-values using a “
by first finding the y-values using a “for” loop and a list. Label your plot and plot legend appropriately. - Consider the sequence whose terms are
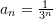 . Use Sympy to evaluate the sum of the first twenty terms. Then, evaluate the infinite sum:
. Use Sympy to evaluate the sum of the first twenty terms. Then, evaluate the infinite sum:![Rendered by QuickLaTeX.com \[\sum_{n=1}^\infty a_n\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-869bd9049377e07c2f2e3ef7e7d38487_l3.png)
Use Matplotlib to plot the first ten terms of the ordered pairs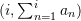 . Label the plot appropriately.
. Label the plot appropriately. - Consider the matrix
![Rendered by QuickLaTeX.com \[M=\left(\begin{matrix}1 & x\\ x & 1\end{matrix}\right)\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4bb7847506bed29f8127a442cf11bb40_l3.png)
Use Matplotlib and Sympy to plot the relationship between the determinant of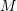 and
and  for
for ![Rendered by QuickLaTeX.com x\in[-5,5]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-578dd5c0f0c4f35b8dd518ad9b002eff_l3.png) . Label the plot appropriately. From the plot, can you identify the values of
. Label the plot appropriately. From the plot, can you identify the values of  for which the determinant is equal to zero?
for which the determinant is equal to zero? - The
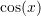 function where
function where  is in radian can be represented as the infinite series:
is in radian can be represented as the infinite series:![Rendered by QuickLaTeX.com \[\cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n)!}x^{2n}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b4c80292b8ea464680cc271934e985f9_l3.png)
Let i+1 be the number of terms used to approximate the function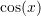 . Using Numpy, create a function in Python whose inputs are
. Using Numpy, create a function in Python whose inputs are  and
and  and whose output is the approximation:
and whose output is the approximation:![Rendered by QuickLaTeX.com \[Approxcos(x,i)=\sum_{n=0}^{i}\frac{(-1)^n}{(2n)!}x^{2n}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-93a705dcdbd33f8241030a789ab89a12_l3.png)
Show using numerical examples that your function gives proper approximations by comparing its output with the built-in function in Numpy.
function in Numpy.
Extra Practice Problems
- The
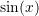 function where
function where  is in radian can be represented as the infinite series:
is in radian can be represented as the infinite series:![Rendered by QuickLaTeX.com \[\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots = \sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)!}x^{2n+1}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-311ea9dba68fdc6341df3d8f8a7494db_l3.png)
Let i+1 be the number of terms used to approximate the function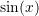 . Using Numpy, create a function in Python whose inputs are
. Using Numpy, create a function in Python whose inputs are  and
and  and whose output is the approximation:
and whose output is the approximation:![Rendered by QuickLaTeX.com \[Approxsin(x,i)=\sum_{n=0}^i\frac{(-1)^n}{(2n+1)!}x^{2n+1}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-aa8bc35f8b194276c7eb785e5d747b81_l3.png)
Show using numerical examples that your function gives proper approximations by comparing its output with the built-in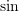 function in Numpy.
function in Numpy. - The discharge velocity through an orifice at the bottom of a water tank open to the atmosphere is given by the relationship:
![Rendered by QuickLaTeX.com \[v=\sqrt{2gh}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-65212c630171db21062d9855e93e8b40_l3.png)
where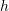 is the height of the water left in the tank. If
is the height of the water left in the tank. If 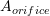 is the “effective” area of the orifice and
is the “effective” area of the orifice and 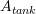 is the cross sectional area of the tank, then the following differential equation describes the rate of change of the height of the water left in the tank
is the cross sectional area of the tank, then the following differential equation describes the rate of change of the height of the water left in the tank![Rendered by QuickLaTeX.com \[\frac{\mathrm{d}h}{\mathrm{d}t}=-\frac{A_{orifice}}{A_{tank}}v\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-15f16c989e7be666f7bd5fad4706e310_l3.png)
Assuming that at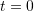 the height of the water in the tank is given by
the height of the water in the tank is given by 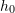 , use the Sympy’s
, use the Sympy’s dsolvefunction to solve the above differential equation using Python to find the height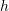 as a function of
as a function of 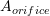 ,
, 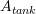 ,
, 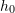 ,
,  , and
, and  . Then, use the “Solve” function to show that the time
. Then, use the “Solve” function to show that the time  to empty the tank (i.e., the time at which
to empty the tank (i.e., the time at which 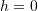 ) is given by the expression:
) is given by the expression:![Rendered by QuickLaTeX.com \[t_e=\sqrt{\frac{2h_0}{g}}\frac{A_{tank}}{A_{orifice}}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-bf4effa3245dc5435a8a0353c23cad33_l3.png)
- In Sympy or Numpy, write two functions in Python whose arguments are a matrix and a vector. The first function should output the matrix after replacing the last row with the given vector. The second function should output the matrix after replacing the last column with the given vector.
