Ordinary Differential Equations: Solving Systems of IVPs
Solving Systems of IVPs
Many engineering problems contain systems of IVPs in which more than one dependent variable is a function of one independent variable, say ![]() . For example, chemical reactions of more than one component are usually described using systems of IVPs in which the initial conditions are known. Similarly, the interaction of biological growth of different species (predators and prey) is usually represented by a system of IVPs in which the initial conditions are given. Generally, these systems can be represented as:
. For example, chemical reactions of more than one component are usually described using systems of IVPs in which the initial conditions are known. Similarly, the interaction of biological growth of different species (predators and prey) is usually represented by a system of IVPs in which the initial conditions are given. Generally, these systems can be represented as:
![Rendered by QuickLaTeX.com \[\begin{split}\frac{\mathrm{d}x_1}{\mathrm{d}t}&=F_1(x_1,x_2,\cdots,x_n,t)\\\frac{\mathrm{d}x_2}{\mathrm{d}t}&=F_2(x_1,x_2,\cdots,x_n,t)\\&\vdots\\\frac{\mathrm{d}x_n}{\mathrm{d}t}&=F_n(x_1,x_2,\cdots,x_n,t)\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-22c12fe0a430fd90b72c47102c122559_l3.png)
The independent variable is discretized such that ![]() with a constant step
with a constant step ![]() . In such systems, the initial conditions, namely the values of
. In such systems, the initial conditions, namely the values of ![]() , are given. The values of
, are given. The values of ![]() when
when ![]() are denoted:
are denoted: ![]() . In this case, the values of the dependent variables at
. In this case, the values of the dependent variables at ![]() can be obtained using the following system of equations:
can be obtained using the following system of equations:
![Rendered by QuickLaTeX.com \[\begin{split}x_1^{(i+1)}&=x_1^{(i)}+\phi_1h\\x_2^{(i+1)}&=x_2^{(i)}+\phi_2h\\&\vdots\\x_n^{(i+1)}&=x_n^{(i)}+\phi_nh\\\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e5dda044bd4f5ba870c24b058d1bed35_l3.png)
where
![Rendered by QuickLaTeX.com \[\begin{split}\phi_1&=F_1(x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)},t_i)\\\phi_2&=F_2(x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)},t_i)\\&\vdots\\\phi_n&=F_n(x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)},t_i)\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1a0d89d31fb044129ee5f4c758092f8b_l3.png)
Alternatively, if the classical Runge-Kutta method is used, then:
![Rendered by QuickLaTeX.com \[\begin{split}\phi_1&=\frac{1}{6}(k_{11}+2k_{12}+2k_{13}+k_{14})\\\phi_2&=\frac{1}{6}(k_{21}+2k_{22}+2k_{23}+k_{24})\\&\vdots\\\phi_n&=\frac{1}{6}(k_{n1}+2k_{n2}+2k_{n3}+k_{n4})\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3bd6807caf02eadc957fdd09d84f13b1_l3.png)
where
It should also be noted that higher-order IVPs can be solved by converting them into a system of first-order IVPs. For example, consider the IVP:
![]()
with the initial conditions
![Rendered by QuickLaTeX.com \[\begin{split}\frac{\mathrm{d}x}{\mathrm{d}t}&=y\\\frac{\mathrm{d}y}{\mathrm{d}t}&=F(x,t)\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ae0c5b101cbdf6ec9751ea0074922f91_l3.png)
with initial conditions given for
Example
Consider the damped spring-mass mechanical system with ![]() ,
, ![]() with the initial conditions
with the initial conditions ![]() and
and ![]() . Find the numerical solution for the position
. Find the numerical solution for the position ![]() and the velocity
and the velocity ![]() for
for ![]() using the explicit Euler method and the Runge-Kutta method. Use
using the explicit Euler method and the Runge-Kutta method. Use ![]() .
.
Solution
The differential equation of the damped system is given by:
![]()
The exact solution can be obtained analytically as:
![]()
Notice that this is a second order ODE. To find the numerical solution, the equation will be converted into a system of 2 IVPs. Setting
![Rendered by QuickLaTeX.com \[\begin{split}\frac{\mathrm{d}x}{\mathrm{d}t}&=y\\\frac{\mathrm{d}y}{\mathrm{d}t}&=-0.15y-x\\\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-99b66e1e4a84b1495b4cde315e1d4264_l3.png)
with the initial conditions ![]() and
and ![]() . With
. With ![]() , the interval can be split into
, the interval can be split into ![]() time steps. The time discretization will be such that
time steps. The time discretization will be such that ![]() ,
, ![]() ,
, ![]() , up to
, up to ![]() . The corresponding positions are given by:
. The corresponding positions are given by: ![]() while the corresponding velocities are given by:
while the corresponding velocities are given by: ![]() .
.
Explicit Euler Method
Using the explicit Euler method, the values of ![]() and
and ![]() can be evaluated as:
can be evaluated as:
![Rendered by QuickLaTeX.com \[\begin{split}x_{i+1}&=x_i+h\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{(x_i,y_i,t_i)}=x_i+hy_i\\y_{i+1}&=y_i+h\frac{\mathrm{d}y}{\mathrm{d}t}\bigg|_{(x_i,y_i,t_i)}=y_i+h(-0.15y_i-x_i)\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-6aa9254d81827eebd352990513ba95e2_l3.png)
With the initial conditions
![]()
Similarly, the values of
![]()
Proceeding iteratively, the values of ![]() and
and ![]() up to
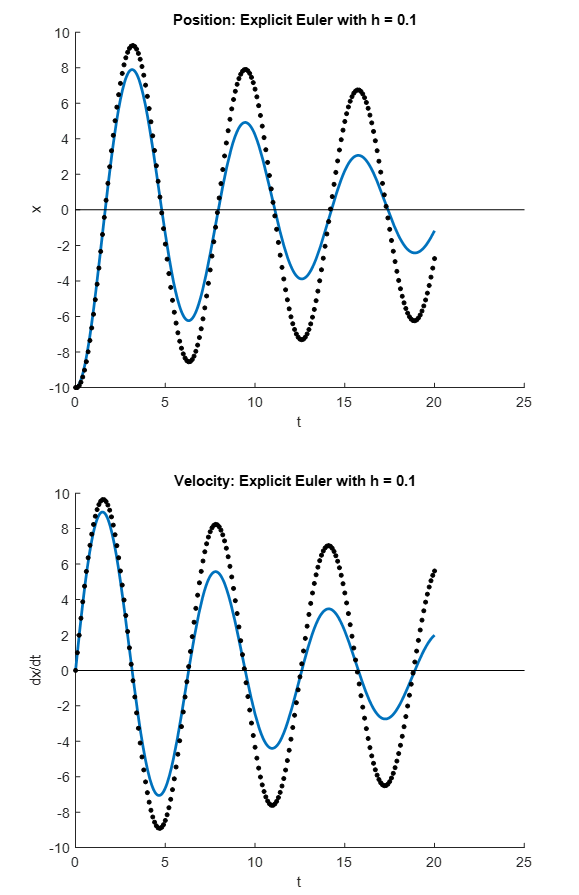
up to ![]() can be obtained. The following figure shows the position (top) and velocity (bottom) obtained with the Explicit Euler method with
can be obtained. The following figure shows the position (top) and velocity (bottom) obtained with the Explicit Euler method with ![]() (black dots) compared to the exact solution (blue line). The Microsoft Excel file EulerSystem.xlsx shows the obtained values.
(black dots) compared to the exact solution (blue line). The Microsoft Excel file EulerSystem.xlsx shows the obtained values.
Classical Runge-Kutta method
The two differential equations are designated ![]() and
and ![]() as follows:
as follows:
![Rendered by QuickLaTeX.com \[\begin{split}F_1(x,y,t)&=\frac{\mathrm{d}x}{\mathrm{d}t}=y\\F_2(x,y,t)&=\frac{\mathrm{d}y}{\mathrm{d}t}=-0.15y-x\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9f404a09415a8d31a693fb1a64aca248_l3.png)
Using the classical Runge-Kutta method, the values of
![Rendered by QuickLaTeX.com \[\begin{split}x_{i+1}&=x_i+\frac{h}{6}(k_{11}+2k_{12}+2k_{13}+k_{14})\\y_{i+1}&=y_i+\frac{h}{6}(k_{21}+2k_{22}+2k_{23}+k_{24}\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7ff222019ec24a496a23f7b003f910ee_l3.png)
where:
![Rendered by QuickLaTeX.com \[\begin{split}k_{11}&=F_1(x_i,y_i,t_i)=y_i\\k_{21}&=F_2(x_i,y_i,t_i)=-0.15y_i-x_i\\k_{12}&=F_1\left(x_i+\frac{h}{2}k_{11},y_i+\frac{h}{2}k_{21},t_i+\frac{h}{2}\right)=y_i+\frac{h}{2}k_{21}\\k_{22}&=F_2\left(x_i+\frac{h}{2}k_{11},y_i+\frac{h}{2}k_{21},t_i+\frac{h}{2}\right)=-0.15(y_i+\frac{h}{2}k_{21})-(x_i+\frac{h}{2}k_{11})\\k_{13}&=F_1\left(x_i+\frac{h}{2}k_{12},y_i+\frac{h}{2}k_{22},t_i+\frac{h}{2}\right)=y_i+\frac{h}{2}k_{22}\\k_{23}&=F_2\left(x_i+\frac{h}{2}k_{12},y_i+\frac{h}{2}k_{22},t_i+\frac{h}{2}\right)=-0.15(y_i+\frac{h}{2}k_{22})-(x_i+\frac{h}{2}k_{12})\\k_{14}&=F_1(x_i+hk_{13},y_i+hk_{23},t_i+h)=y_i+hk_{23}\\k_{24}&=F_2(x_i+hk_{13},y_i+hk_{23},t_i+h)=-0.15(y_i+hk_{23})-(x_i+hk_{13})\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7b68cc7128ec4072a8b84b336ce5be6f_l3.png)
With the initial conditions
![Rendered by QuickLaTeX.com \[\begin{split}k_{11}&=y_0=0\\k_{21}&=-0.15y_0-x_0=10\\k_{12}&=y_0+\frac{h}{2}k_{21}=0+0.05\times 10=0.5\\k_{22}&=-0.15(y_0+\frac{h}{2}k_{21})-(x_0+\frac{h}{2}k_{11})\\&=-0.15(0+0.05\times 10)-(-10+0.05\times 0)=9.925\\k_{13}&=y_0+\frac{h}{2}k_{22}=0+0.05(9.925)=0.49625\\k_{23}&=-0.15(y_0+\frac{h}{2}k_{22})-(x_0+\frac{h}{2}k_{12})\\&=-0.15(0+0.05\times 9.925)-(-10+0.05\times 0.5)=9.90056\\k_{14}&=y_0+hk_{23}=0+0.1\times 9.90056=0.990056\\k_{24}&=-0.15(y_0+hk_{23})-(x_0+hk_{13})\\&=-0.15(0+0.1\times 9.90056)-(-10+0.1\times 0.49625)=9.80187\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a3f7886e5b7cc5c0a2f7813ac930d824_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[\begin{split}x_1&=x_0+\frac{h}{6}(k_{11}+2k_{12}+2k_{13}+k_{14})\\&=-10+\frac{0.1}{6}(0+2\times 0.5+2\times 0.49625+0.990056)=-9.9503\\y_1&=y_0+\frac{h}{6}(k_{21}+2k_{22}+2k_{23}+k_{24})\\&=0+\frac{0.1}{6}(10+2\times 9.925+2\times 9.90056+9.80187)=0.990883\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2670507993deb7cccdd05ef55ae8f404_l3.png)
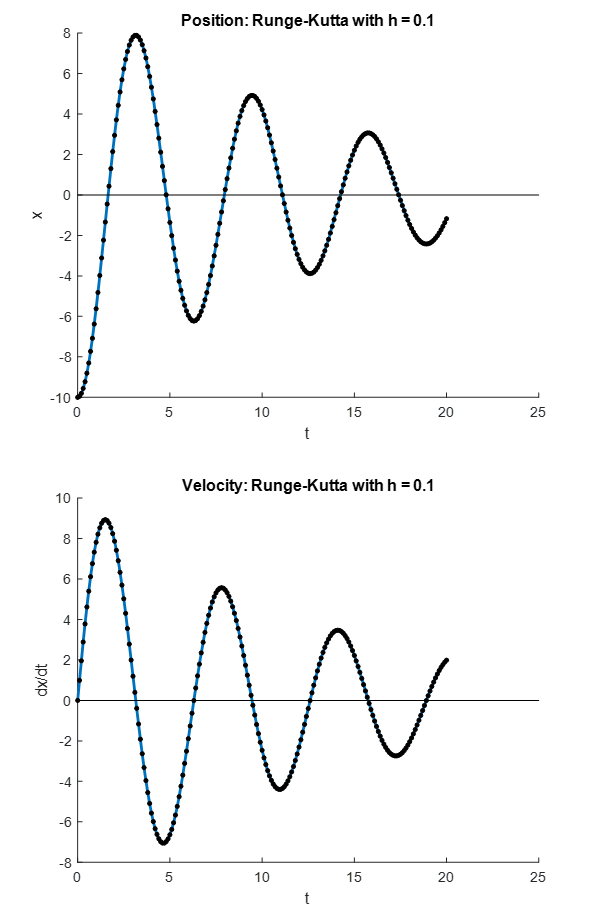
Proceeding iteratively, the values of
Comparison
From the figures above, it is evident that using the explicit Euler method, the numerical solution deviates from the exact solution for higher values of ![]() . However, the classical Runge-Kutta method provides very accurate predictions.
. However, the classical Runge-Kutta method provides very accurate predictions.
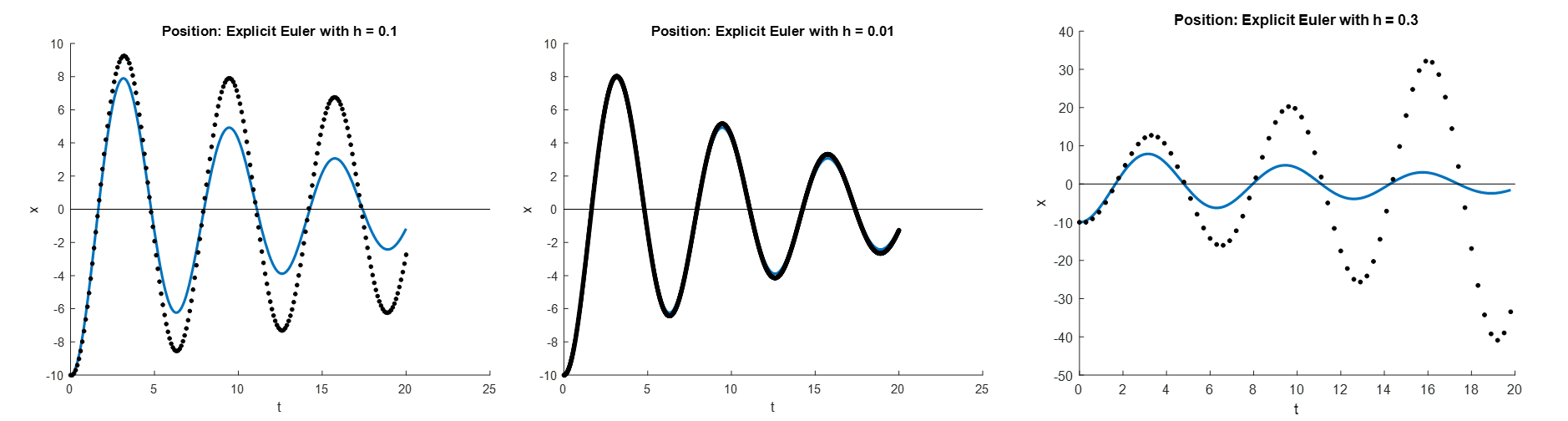
As shown in the figure below, the Explicit Euler method can produce results with higher accuracy using smaller values of the step size (i.e. ![]() ). With higher values of the step size, the method can become unstable and grow without bound (i.e.
). With higher values of the step size, the method can become unstable and grow without bound (i.e. ![]() ).
).
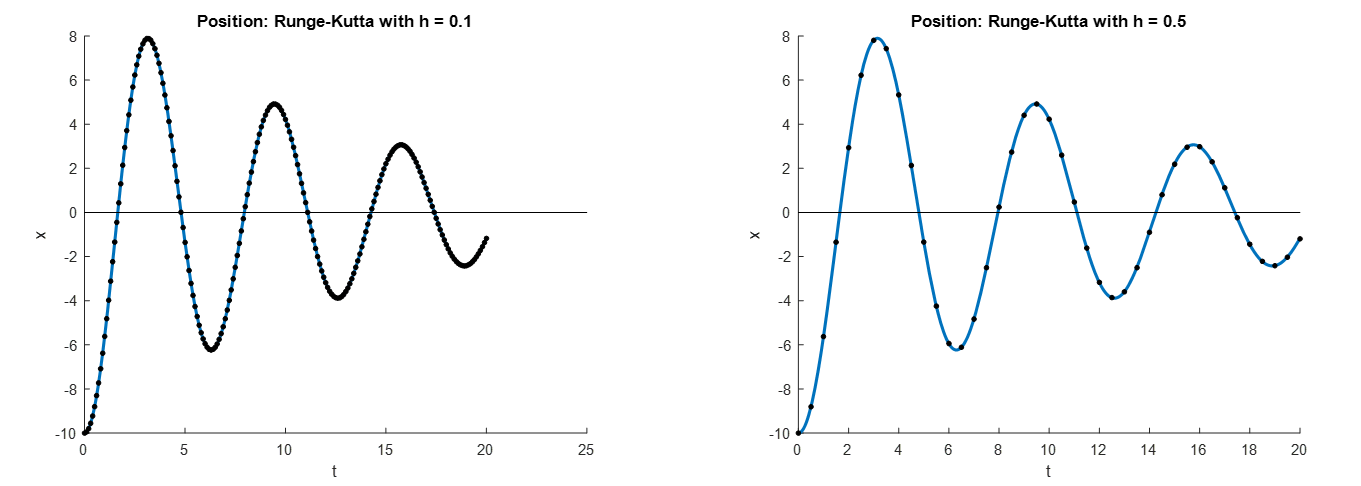
In contrast, the figure below demonstrates that the classical Runge-Kutta method is able to produce accurate results and maintain numerical stability for a step size as high as ![]() .
.
The Mathematica code utilized to produce the curves is shown below.
View Mathematica CodeClear[x]
a = DSolve[{Derivative[2][x][t] == -(0.15*Derivative[1][x][t]) - x[t], Derivative[1][x][0] == 0, x[0] == -10}, x, t]
x = x[t] /. a[[1]]
xp = Simplify[D[x, {t}]]
Plot[x, {t, 0, 20}, AxesOrigin -> {0, 0}, AxesOrigin -> {0, 0}, AxesLabel -> {"time", "x (position)"}]
Plot[xp, {t, 0, 20}, AxesOrigin -> {0, 0}, AxesOrigin -> {0, 0}, AxesLabel -> {"time", "x' (velocity)"}]
EulerMethod2[fp1_, fp2_, x10_, x20_, h_, t0_, tmax_] := (n = (tmax - t0)/h + 1; x1table = Table[0, {i, 1, n}]; x2table = Table[0, {i, 1, n}]; x1table[[1]] = x10; x2table[[1]] = x20;
Do[x1table[[i]] = h*fp1[x1table[[i - 1]], x2table[[i - 1]], h*(i - 2) + t0] + x1table[[i - 1]]; x2table[[i]] = h*fp2[x1table[[i - 1]], x2table[[i - 1]], h*(i - 2) + t0] +
x2table[[i - 1]], {i, 2, n}]; Data = Table[{h*(i - 1) + t0, x1table[[i]], x2table[[i]]}, {i, 1, n}]; Data)
RK4Method2[fp1_, fp2_, x10_, x20_, h_, t0_, tmax_] := (n = (tmax - t0)/h + 1; x1table = Table[0, {i, 1, n}]; x1table[[1]] = x10; x2table = Table[0, {i, 1, n}]; x2table[[1]] = x20;
Do[k11 = fp1[x1table[[i - 1]], x2table[[i - 1]], h*(i - 2) + t0]; k21 = fp2[x1table[[i - 1]], x2table[[i - 1]], h*(i - 2) + t0];
k12 = fp1[(h*k11)/2 + x1table[[i - 1]], (h*k21)/2 + x2table[[i - 1]], h*(i - 1.5) + t0]; k22 = fp2[(h*k11)/2 + x1table[[i - 1]], (h*k21)/2 + x2table[[i - 1]], h*(i - 1.5) + t0];
k13 = fp1[(h*k12)/2 + x1table[[i - 1]], (h*k22)/2 + x2table[[i - 1]], h*(i - 1.5) + t0]; k23 = fp2[(h*k12)/2 + x1table[[i - 1]], (h*k22)/2 + x2table[[i - 1]], h*(i - 1.5) + t0];
k14 = fp1[h*k13 + x1table[[i - 1]], h*k23 + x2table[[i - 1]], h*(i - 1) + t0]; k24 = fp2[h*k13 + x1table[[i - 1]], h*k23 + x2table[[i - 1]], h*(i - 1) + t0];
x1table[[i]] = (1/6)*h*(k11 + 2*k12 + 2*k13 + k14) + x1table[[i - 1]]; x2table[[i]] = (1/6)*h*(k21 + 2*k22 + 2*k23 + k24) + x2table[[i - 1]], {i, 2, n}];
Data2 = Table[{h*(i - 1) + t0, x1table[[i]], x2table[[i]]}, {i, 1, n}]; Data2)
fp1[x_, y_, t_] := y;
fp2[x_, y_, t_] := -x - 0.15*y;
Data = EulerMethod2[fp1, fp2, -10, 0, 0.1, 0, 20];
DataPosition = Drop[Data, None, {3}];
DataVelocity = Drop[Data, None, {2}];
a1 = Plot[x, {t, 0, 20}, Epilog -> {PointSize[Large], Point[DataPosition]}, AxesOrigin -> {0, 0}, ImageSize -> Medium, AxesLabel -> {"Time", "x (position)"}];
a2 = Plot[xp, {t, 0, 20}, Epilog -> {PointSize[Large], Point[DataVelocity]}, AxesOrigin -> {0, 0}, ImageSize -> Medium, AxesLabel -> {"Time", "x' (velocity)"}];
a = Grid[{{a1, a2}}];
Grid[{{"Explicit Euler"}, {a}}]
Data = RK4Method2[fp1, fp2, -10, 0, 0.1, 0, 20];
DataPosition = Drop[Data, None, {3}];
DataVelocity = Drop[Data, None, {2}];
a1 = Plot[x, {t, 0, 20}, Epilog -> {PointSize[Large], Point[DataPosition]}, ImageSize -> Medium, AxesOrigin -> {0, 0}, AxesLabel -> {"Time", "x (position)"}];
a2 = Plot[xp, {t, 0, 20}, Epilog -> {PointSize[Large], Point[DataVelocity]}, ImageSize -> Medium, AxesOrigin -> {0, 0}, AxesLabel -> {"Time", "x' (velocity)"}];
a = Grid[{{a1, a2}}];
Grid[{{"Classical Runge-Kutta"}, {a}}]
View Python Code
# UPGRADE: need Sympy 1.2 or later, upgrade by running: "!pip install sympy --upgrade" in a code cell
# !pip install sympy --upgrade
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
sp.init_printing(use_latex=True)
x = sp.Function('x')
t = sp.symbols('t')
sol = sp.dsolve(x(t).diff(t,2) + x(t) + 0.15*x(t).diff(t), ics={x(0): -10, x(t).diff(t).subs(t,0): 0})
display(sol)
xp = sp.simplify(sol.rhs.diff(t))
display(xp)
x_val = np.arange(0,20,0.01)
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.xlabel("time"); plt.ylabel("x (position)")
plt.grid(); plt.show()
plt.plot(x_val, [xp.subs(t, i) for i in x_val])
plt.xlabel("time"); plt.ylabel("x' (velocity)")
plt.grid(); plt.show()
def EulerMethod2(fp1, fp2, x10, x20, h, t0, tmax):
n = int((tmax - t0)/h + 1)
x1table = [0 for i in range(n)]
x2table = [0 for i in range(n)]
x1table[0] = x10
x2table[0] = x20
for i in range(1,n):
x1table[i] = x1table[i - 1] + h*fp1(x1table[i - 1], x2table[i - 1], t0 + (i - 1)*h)
x2table[i] = x2table[i - 1] + h*fp2(x1table[i - 1], x2table[i - 1], t0 + (i - 1)*h)
Data = [[t0 + i*h, x1table[i], x2table[i]] for i in range(n)]
return Data
def RK4Method2(fp1, fp2, x10, x20, h, t0, tmax):
n = int((tmax - t0)/h + 1)
x1table = [0 for i in range(n)]
x1table[0] = x10
x2table = [0 for i in range(n)]
x2table[0] = x20
for i in range(1,n):
k11 = fp1(x1table[i - 1], x2table[i - 1], t0 + (i - 1)*h)
k21 = fp2(x1table[i - 1], x2table[i - 1], t0 + (i - 1)*h)
k12 = fp1(x1table[i - 1] + h/2*k11, x2table[i - 1] + h/2*k21, t0 + (i - 0.5)*h)
k22 = fp2(x1table[i - 1] + h/2*k11, x2table[i - 1] + h/2*k21, t0 + (i - 0.5)*h)
k13 = fp1(x1table[i - 1] + h/2*k12, x2table[i - 1] + h/2*k22, t0 + (i - 0.5)*h)
k23 = fp2(x1table[i - 1] + h/2*k12, x2table[i - 1] + h/2*k22, t0 + (i - 0.5)*h)
k14 = fp1(x1table[i - 1] + h*k13, x2table[i - 1] + h*k23, t0 + i*h)
k24 = fp2(x1table[i - 1] + h*k13, x2table[i - 1] + h*k23, t0 + i*h)
x1table[i] = x1table[i - 1] + h*(k11 + 2*k12 + 2*k13 + k14)/6
x2table[i] = x2table[i - 1] + h*(k21 + 2*k22 + 2*k23 + k24)/6
Data = [[t0 + i*h, x1table[i], x2table[i]] for i in range(n)]
return Data
def fp1(x, y, t): return y
def fp2(x, y, t): return -x - 0.15*y
x_val = np.arange(0,20,0.01)
Data = EulerMethod2(fp1, fp2, -10, 0, 0.1, 0, 20)
plt.title("Explicit Euler")
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.scatter([DataPosition[0] for DataPosition in Data],
[DataPosition[1] for DataPosition in Data],c='k')
plt.xlabel("Time"); plt.ylabel("x (position)")
plt.grid(); plt.show()
plt.title("Explicit Euler")
plt.plot(x_val, [xp.subs(t, i) for i in x_val])
plt.scatter([DataVelocity[0] for DataVelocity in Data],
[DataVelocity[2] for DataVelocity in Data],c='k')
plt.xlabel("Time"); plt.ylabel("x' (velocity)")
plt.grid(); plt.show()
Data = RK4Method2(fp1, fp2, -10, 0, 0.1, 0, 20)
plt.title("Classical Runge-Kutta")
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.scatter([DataPosition[0] for DataPosition in Data],
[DataPosition[1] for DataPosition in Data],c='k')
plt.xlabel("Time"); plt.ylabel("x (position)")
plt.grid(); plt.show()
plt.title("Classical Runge-Kutta")
plt.plot(x_val, [xp.subs(t, i) for i in x_val])
plt.scatter([DataVelocity[0] for DataVelocity in Data],
[DataVelocity[2] for DataVelocity in Data],c='k')
plt.xlabel("Time"); plt.ylabel("x' (velocity)")
plt.grid(); plt.show()
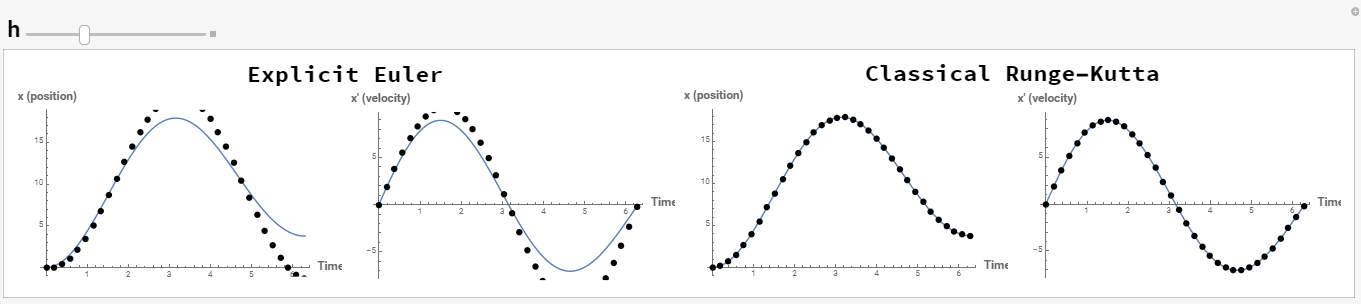
The effect of changing the value of ![]() on the resulting numerical solution for the system of IVPs given here can be illustrated using the following tool. Even for
on the resulting numerical solution for the system of IVPs given here can be illustrated using the following tool. Even for ![]() the classical Runge-Kutta produces very accurate predictions at which point the explicit Euler method produces very erroneous results.
the classical Runge-Kutta produces very accurate predictions at which point the explicit Euler method produces very erroneous results.
Using Mathematica
The built-in NDSolve in Mathematica uses the Runge-Kutta methods to solve a system of IVPs and produces piecewise interpolating polynomials for the dependent variables. The following code solves some of the preceding examples and compares with the exact solution. Note that in those examples when the exact and numerical solutions are plotted together, they overlap!
View Mathematica CodeClear[x, xn, xtable]
(*Example 1*)
k = 0.015;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
b = NDSolve[{xn'[t] == k*xn[t], xn[0] == 35}, xn, {t, 0, 50}]
xn = xn /. b[[1]]
Plot[{x, xn[t]}, {t, 0, 50}, PlotLegends -> {"Exact", "Numerical using Mathematica"}, AxesLabel -> {"t", "Population"}]
(*Example 2*)
Clear[cn]
b = NDSolve[{cn'[t] == (100 + 50*Cos[2 Pi*t/365])/10000*(5 Exp[-2 t/1000] - cn[t]), cn[0] == 5}, cn, {t, 0, 700}]
cn = cn /. b[[1]]
Plot[cn[t], {t, 0, 700}, AxesLabel -> {"t", "Concentration"}]
(*Example 4*)
Clear[xn, x]
a = DSolve[{x'[t] == t*x[t]^2 + 2*x[t], x[0] == -5}, x, t];
x = x[t] /. a[[1]]
b = NDSolve[{xn'[t] == t*xn[t]^2 + 2 xn[t], xn[0] == -5}, xn, {t, 0, 5}]
xn = xn /. b[[1]]
Plot[{x, xn[t]}, {t, 0, 5}, PlotRange -> All, PlotLegends -> {"Exact", "Numerical using Mathematica"}, AxesLabel -> {"t", "x"}]
(*Example of a system*)
Clear[xn, yn, x]
a = DSolve[{x''[t] == 10 - x[t] - 0.15 x'[t], x'[0] == 0, x[0] == 0}, x, t]
x = x[t] /. a[[1]]
xp = Simplify[D[x, t]]
b = NDSolve[{xn'[t] == yn[t], yn'[t] == 10 - xn[t] - 0.15 yn[t], xn[0] == 0, yn[0] == 0}, {xn, yn}, {t, 0, 2 Pi}]
xn = xn /. b[[1]]
yn = yn /. b[[1]]
Plot[{x, xn[t]}, {t, 0, 2 Pi}, AxesOrigin -> {0, 0}, AxesOrigin -> {0, 0}, PlotLegends -> {"Exact", "Numerical using Mathematica"}, AxesLabel -> {"time", "x (position)"}]
Plot[{xp, yn[t]}, {t, 0, 2 Pi}, AxesOrigin -> {0, 0}, AxesOrigin -> {0, 0}, PlotLegends -> {"Exact", "Numerical using Mathematica"}, AxesLabel -> {"time", "x' (velocity)"}]
View Python Code
# UPGRADE: need Sympy 1.2 or later, upgrade by running: "!pip install sympy --upgrade" in a code cell
# !pip install sympy --upgrade
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from scipy.integrate import odeint
sp.init_printing(use_latex=True)
x = sp.Function('x')
t, k = sp.symbols('t k')
# Example 1
k = 0.015
a = sp.dsolve(x(t).diff(t) - k*x(t), ics={x(0): 35})
display(a)
def f(x, t, params):
k = params
dxdt = k*x
return dxdt
x_val = np.arange(0,50,0.1)
b = odeint(f, [35], x_val, args=(k,))
plt.plot(x_val, [a.subs(t, i).rhs for i in x_val], label="Exact")
plt.plot(x_val, b, label="Numerical")
plt.xlabel("t"); plt.ylabel("Population")
plt.legend(); plt.grid(); plt.show()
# Example 2
def f(c, t):
dcdt = (100 + 50*np.cos(2*np.pi*t/365))/10000*(5*np.exp(-2*t/1000) - c)
return dcdt
x_val = np.arange(0,700,0.1)
b = odeint(f, [5], x_val)
plt.plot(x_val, b)
plt.xlabel("t"); plt.ylabel("Concentration")
plt.grid(); plt.show()
# Example 4
a = sp.dsolve(x(t).diff(t) - t*x(t)**2 - 2*x(t), ics={x(0): -5})
display(a)
def f(x, t):
dxdt = t*x**2 + 2*x
return dxdt
x_val = np.arange(0,5,0.1)
b = odeint(f, [-5], x_val)
plt.plot(x_val, [a.subs(t, i).rhs for i in x_val], label="Exact")
plt.plot(x_val, b, label="Numerical")
plt.xlabel("t"); plt.ylabel("x")
plt.legend(); plt.grid(); plt.show()
# Example of a system
a = sp.dsolve(x(t).diff(t,2) - 10 + x(t) + 0.15*x(t).diff(t), ics={x(t).diff(t).subs(t,0): 0, x(0): 0})
ap = sp.diff(a.rhs,t)
display(a)
display(ap)
def f(vars, t):
x, y = vars
dxdt = y
dydt = 10 - x - 0.15*y
return [dxdt, dydt]
x_val = np.arange(0,2*np.pi,0.1)
b = odeint(f, [0,0], x_val)
xn = b[:, 0]
yn = b[:, 1]
plt.plot(x_val, [a.subs(t, i).rhs for i in x_val], label="Exact")
plt.plot(x_val, xn, label="Numerical")
plt.xlabel("Time"); plt.ylabel("x (position)")
plt.legend(); plt.grid(); plt.show()
plt.plot(x_val, [ap.subs(t, i) for i in x_val], label="Exact")
plt.plot(x_val, yn, label="Numerical")
plt.xlabel("Time"); plt.ylabel("x' (velocity)")
plt.legend(); plt.grid(); plt.show()
Lecture Video