Solution Methods for IVPs: Backward (Implicit) Euler Method
Backward (Implicit) Euler Method
Consider the following IVP:
![]()
Assuming that the value of the dependent variable ![]() (say
(say ![]() ) is known at an initial value
) is known at an initial value ![]() , then, we can use a Taylor approximation to relate the value of
, then, we can use a Taylor approximation to relate the value of ![]() at
at ![]() , namely
, namely ![]() with
with ![]() . However, unlike the explicit Euler method, we will use the Taylor series around the point
. However, unlike the explicit Euler method, we will use the Taylor series around the point ![]() , that is:
, that is:
![]()
Substituting the differential equation into the above equation yields:
![]()
Therefore, as an approximation, an estimate for ![]() can be taken as
can be taken as ![]() as follows:
as follows:
![]()
Using this estimate, the local truncation error is thus proportional to the square of the step size with the constant of proportionality related to the second derivative of ![]() , which is the first derivative of the given IVP. The backward Euler method is termed an “implicit” method because it uses the slope
, which is the first derivative of the given IVP. The backward Euler method is termed an “implicit” method because it uses the slope ![]() at the unknown point
at the unknown point ![]() , namely:
, namely: ![]() . The developed equation can be linear in
. The developed equation can be linear in ![]() or nonlinear. Nonlinear equations can often be solved using the fixed-point iteration method or the Newton-Raphson method to find the value of
or nonlinear. Nonlinear equations can often be solved using the fixed-point iteration method or the Newton-Raphson method to find the value of ![]() . While the implicit scheme does not provide better accuracy than the explicit scheme, it comes with additional computations. However, one advantage is that this scheme is always stable.
. While the implicit scheme does not provide better accuracy than the explicit scheme, it comes with additional computations. However, one advantage is that this scheme is always stable.
The following Mathematica code adopts the implicit Euler scheme and uses the built-in FindRoot function to solve for ![]() . The code is similar to the code provided for the explicit scheme except for the line to calculate
. The code is similar to the code provided for the explicit scheme except for the line to calculate ![]() .
.
ImplicitEulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[ s = FindRoot[x == xtable[[i - 1]] + h*fp[x, t0 + (i - 1) h], {x, xtable[[i - 1]]}]; xtable[[i]] = x /. s[[1]], {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
function1[y_, t_] := 0.05 y
function2[x_, t_] := 0.015 x
ImplicitEulerMethod[function1, 35, 1.0, 0, 50] // MatrixForm
ImplicitEulerMethod[function2, 35, 1.0, 0, 50] // MatrixForm
import numpy as np
import sympy as sp
x = sp.symbols('x')
def ImplicitEulerMethod(fp, x0, h, t0, tmax):
n = int((tmax - t0)/h + 1)
xtable = [0 for i in range(n)]
xtable[0] = x0
for i in range(1,n):
s = sp.nsolve(x - xtable[i - 1] - h*fp(x, t0 + i*h), x, xtable[i - 1])
xtable[i] = s
Data = [[t0 + i*h, xtable[i]] for i in range(n)]
return Data
def function1(y, t): return 0.05*y
def function2(x, t): return 0.015*x
print(np.vstack(ImplicitEulerMethod(function1, 35, 1.0, 0, 50)))
print(np.vstack(ImplicitEulerMethod(function2, 35, 1.0, 0, 50)))
Example 1
Repeat Example 1 above using the implicit Euler method.
Solution
When ![]() , the IVP is given by:
, the IVP is given by:
![]()
Given a value for ![]() at
at ![]() , and taking
, and taking ![]() , the estimate for
, the estimate for ![]() can be calculated according to the formula:
can be calculated according to the formula:
![]()
Rearranging yields:
![]()
With ![]() million and
million and ![]() years, the estimate for the population at
years, the estimate for the population at ![]() years using the implicit Euler method is given by:
years using the implicit Euler method is given by:
![]()
at ![]() years, the value of
years, the value of ![]() in millions is given by:
in millions is given by:
![]()
Proceeding iteratively, the following is the Excel table showing the values of the population up to ![]() years.
years.
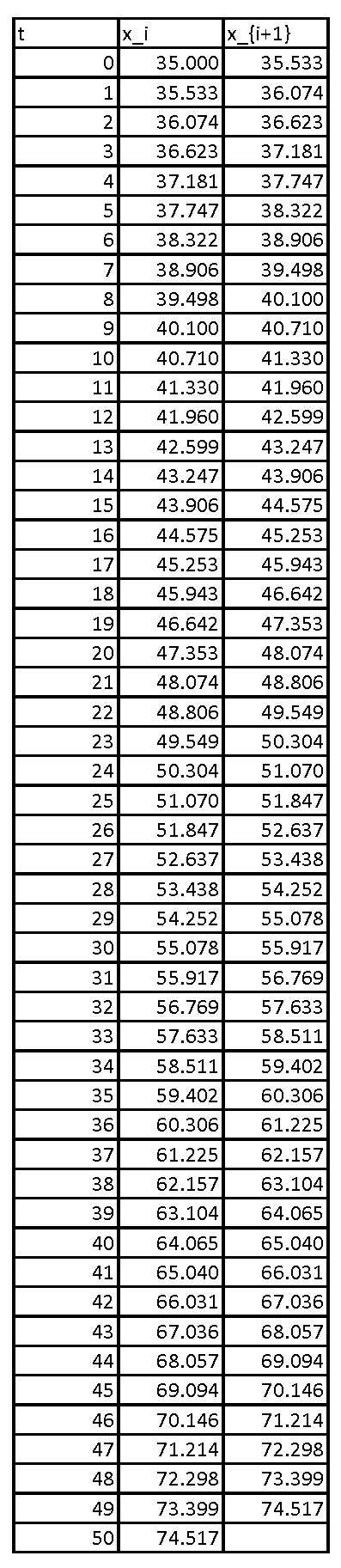
When ![]() , the implicit method provides an error similar to that of the explicit method:
, the implicit method provides an error similar to that of the explicit method:
![Rendered by QuickLaTeX.com \[\begin{split}E&=35e^{(0.015\times 50)}-74.517=74.095-74.517=-0.4\\E_r&=\frac{-0.4}{74.095}=-0.005\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f0b733de9c52ab9b9acb05d7cca0c663_l3.png)
When ![]() , the IVP is given by:
, the IVP is given by:
![]()
Given a value for ![]() at
at ![]() , and taking
, and taking ![]() , the estimate for
, the estimate for ![]() can be calculated according to the formula:
can be calculated according to the formula:
![]()
Rearranging yields:
![]()
With ![]() million and
million and ![]() years, the estimate for the population at
years, the estimate for the population at ![]() years using the implicit Euler method is given by:
years using the implicit Euler method is given by:
![]()
at ![]() years, the value of
years, the value of ![]() in millions is given by:
in millions is given by:
![]()
Proceeding iteratively, the following is the Excel table showing the values of the population up to ![]() years.
years.
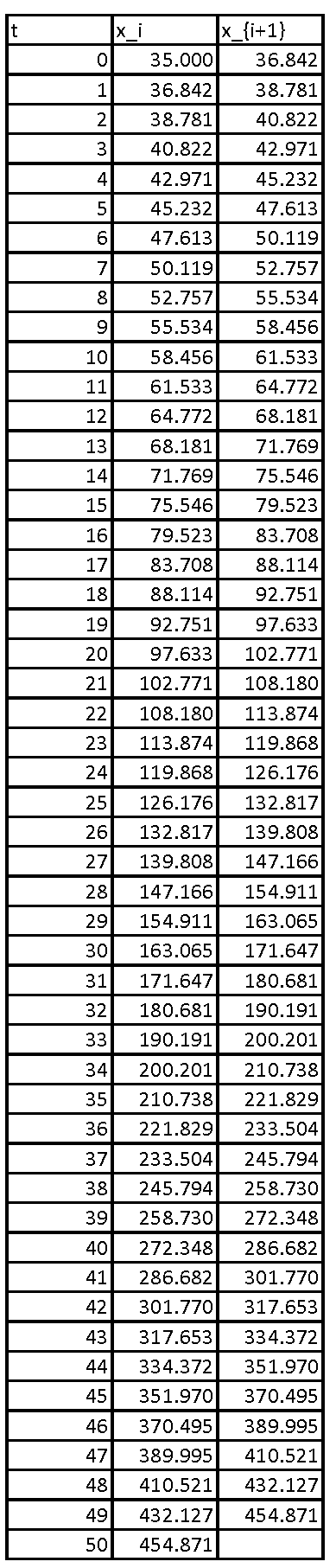
Again, the error produced by the implicit method is comparable to that produced by the explicit method shown above:
![Rendered by QuickLaTeX.com \[\begin{split}E&=35e^{(0.05\times 50)}-454.871=426.387-454.871=-28.483\\E_r&=\frac{-28.483}{426.387}=-0.07\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-184f0f699f2007d0cfcc2e8db299a035_l3.png)
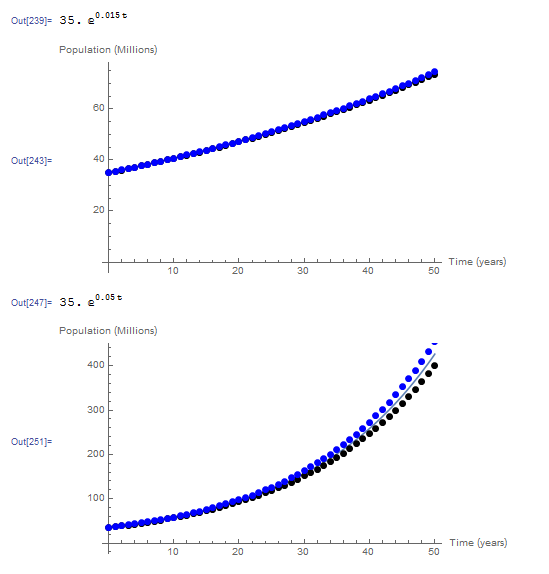
The following is the graph showing the exact solution versus the data using both the implicit (blue dots) and the explicit (black dots) Euler method for both values of ![]() .
.
View Mathematica Code
EulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[xtable[[i]] = xtable[[i - 1]] + h*fp[xtable[[i - 1]], t0 + (i - 2) h], {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
ImplicitEulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[s = FindRoot[x == xtable[[i - 1]] + h*fp[x, t0 + (i - 1) h], {x, xtable[[i - 1]]}]; xtable[[i]] = x /. s[[1]], {i, 2, n}];
Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data2)
Clear[x, xtable]
k = 0.015;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := k*x;
Data = EulerMethod[fp, 35, 1.0, 0, 50];
Data2 = ImplicitEulerMethod[fp, 35, 1.0, 0, 50];
Plot[x, {t, 0, 50}, Epilog -> {PointSize[Large], Point[Data], Blue, Point[Data2]}, AxesOrigin -> {0, 0}, AxesLabel -> {"Time (years)", "Population (Millions)"}]
Clear[x, xtable]
k = 0.05;
a = DSolve[{x'[t] == k*x[t], x[0] == 35}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := k*x;
Data = EulerMethod[fp, 35, 1.0, 0, 50];
Data2 = ImplicitEulerMethod[fp, 35, 1.0, 0, 50];
Plot[x, {t, 0, 50}, Epilog -> {PointSize[Large], Point[Data], Blue, Point[Data2]}, AxesOrigin -> {0, 0}, AxesLabel -> {"Time (years)", "Population (Millions)"}]
# UPGRADE: need Sympy 1.2 or later, upgrade by running: "!pip install sympy --upgrade" in a code cell
# !pip install sympy --upgrade
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
sp.init_printing(use_latex=True)
def EulerMethod(fp, x0, h, t0, tmax):
n = int((tmax - t0)/h + 1)
xtable = [0 for i in range(n)]
xtable[0] = x0
for i in range(1,n):
xtable[i] = xtable[i - 1] + h*fp(xtable[i - 1], t0 + (i - 1)*h)
Data = [[t0 + i*h, xtable[i]] for i in range(n)]
return Data
def ImplicitEulerMethod(fp, x0, h, t0, tmax):
n = int((tmax - t0)/h + 1)
xtable = [0 for i in range(n)]
xtable[0] = x0
x = sp.symbols('x')
for i in range(1,n):
s = sp.nsolve(x - xtable[i - 1] - h*fp(x, t0 + i*h), x, xtable[i - 1])
xtable[i] = s
Data = [[t0 + i*h, xtable[i]] for i in range(n)]
return Data
x = sp.Function('x')
t = sp.symbols('t')
k = 0.015
sol = sp.dsolve(x(t).diff(t) - k*x(t), ics={x(0): 35})
display(sol)
def fp(x, t): return k*x
Data = EulerMethod(fp, 35, 1.0, 0, 50)
Data2 = ImplicitEulerMethod(fp, 35, 1.0, 0, 50)
x_val = np.arange(0,50,0.1)
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.scatter([point[0] for point in Data],[point[1] for point in Data])
plt.scatter([point[0] for point in Data2],[point[1] for point in Data2])
plt.xlabel("Time (years)"); plt.ylabel("Population (Millions)")
plt.grid(); plt.show()
k = 0.05
sol = sp.dsolve(x(t).diff(t) - k*x(t), ics={x(0): 35})
display(sol)
Data = EulerMethod(fp, 35, 1.0, 0, 50)
Data2 = ImplicitEulerMethod(fp, 35, 1.0, 0, 50)
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.scatter([point[0] for point in Data],[point[1] for point in Data])
plt.scatter([point[0] for point in Data2],[point[1] for point in Data2])
plt.xlabel("Time (years)"); plt.ylabel("Population (Millions)")
plt.grid(); plt.show()
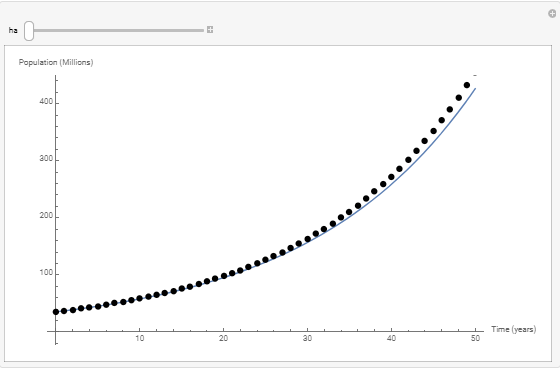
The following tool illustrates the effect of choosing the step size ![]() on the difference between the numerical solution obtained using the implicit methods (shown as dots) and the exact solution (shown as the blue curve) for the case when
on the difference between the numerical solution obtained using the implicit methods (shown as dots) and the exact solution (shown as the blue curve) for the case when ![]() . The smaller the step size, the more accurate the solution is. The higher the value of
. The smaller the step size, the more accurate the solution is. The higher the value of ![]() , the more the numerical solution deviates from the exact solution. The error increases away from the initial conditions.
, the more the numerical solution deviates from the exact solution. The error increases away from the initial conditions.
Example 2
Repeat Example 2 above using the implicit Euler method.
Solution
Recall that the IVP for this problem is given by:
![]()
Taking ![]() day,
day, ![]() can be predicted for a given value of
can be predicted for a given value of ![]() using the implicit Euler method as follows:
using the implicit Euler method as follows:
![]()
Rearranging:
![Rendered by QuickLaTeX.com \[c_{i+1}=\frac{c_i+\frac{\left(100+50\cos{(2\pi t_{i+1}/365)}\right)}{10000}\left(5e^{\left(\frac{-2t_{i+1}}{1000}\right)}\right)}{1+\frac{\left(100+50\cos{(2\pi t_{i+1}/365)}\right)}{10000}}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-92fa4bbacfc7d8a2a576b67f18a1a7ce_l3.png)
With ![]() and
and ![]() ppb,
ppb, ![]() is calculated as:
is calculated as:
![Rendered by QuickLaTeX.com \[ c_1=\frac{5+0.015\left(5e^{\left(\frac{-2(1)}{1000}\right)}\right)}{1+0.015}=4.9999\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-330bc870bcb2f2c68dbedb797d655884_l3.png)
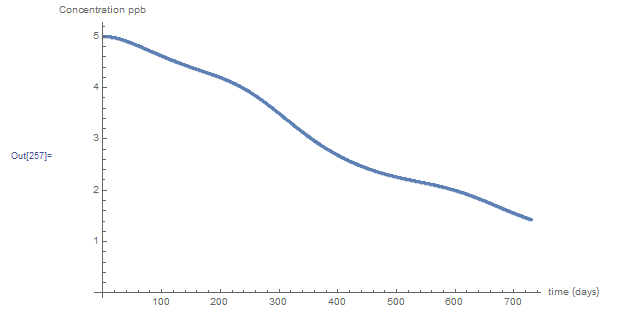
Proceeding iteratively produces the following graph with results almost identical to those produced by the explicit method. You can download the Microsoft Excel file example2implicit.xlsx showing the calculations.
 View Mathematica Code
View Mathematica CodeImplicitEulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[s = FindRoot[x == xtable[[i - 1]] + h*fp[x, t0 + (i - 1) h], {x, xtable[[i - 1]]}]; xtable[[i]] = x /. s[[1]], {i, 2, n}];
Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data)
f[t_] := 100 + 50*Cos[2 Pi*t/365];
cin[t_] := 5 E^(-2 t/1000);
fp[c_, t_] := f[t] (cin[t] - c)/10000;
Data = ImplicitEulerMethod[fp, 5, 1, 0, 365*2];
ListPlot[Data, AxesLabel -> {"time (days)", "Concentration ppb"}]
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
def ImplicitEulerMethod(fp, x0, h, t0, tmax):
n = int((tmax - t0)/h + 1)
xtable = [0 for i in range(n)]
xtable[0] = x0
x = sp.symbols('x')
for i in range(1,n):
s = sp.nsolve(x - xtable[i - 1] - h*fp(x, t0 + i*h), x, xtable[i - 1])
xtable[i] = s
Data = [[t0 + i*h, xtable[i]] for i in range(n)]
return Data
def f(t): return 100 + 50*np.cos(2*np.pi*t/365)
def cin(t): return 5*np.exp(-2*t/1000)
def fp(c, t): return f(t)*(cin(t) - c)/10000
Data = ImplicitEulerMethod(fp, 5, 1, 0, 365*2)
plt.scatter([point[0] for point in Data],[point[1] for point in Data])
plt.xlabel("Time (days)"); plt.ylabel("Concentration ppb")
plt.grid(); plt.show()
Example 3
We will repeat Example 3 above to illustrate that the implicit Euler method is always stable.
Consider the IVP of the form:
![]()
If
Solution
Using an implicit Euler scheme, the value of ![]() can be obtained as follows:
can be obtained as follows:
![]()
Therefore:
![]()
![]() is a positive number. Therefore, the term
is a positive number. Therefore, the term ![]() is bounded for every
is bounded for every ![]() and therefore,
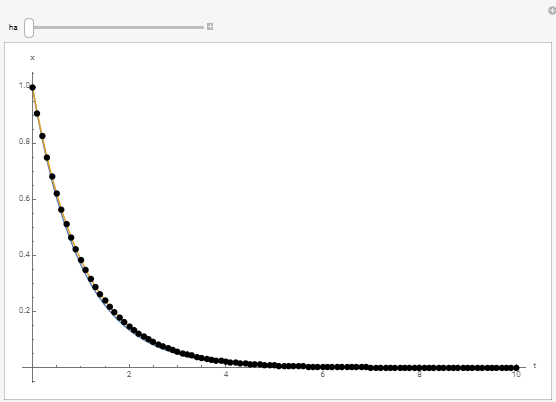
and therefore, ![]() is bounded. The following tool illustrates the difference between the obtained result for
is bounded. The following tool illustrates the difference between the obtained result for ![]() . Vary the value of
. Vary the value of ![]() and notice how the obtained solution (black dots) compares to the exact solution (blue curve). While the accuracy is lost with higher values of
and notice how the obtained solution (black dots) compares to the exact solution (blue curve). While the accuracy is lost with higher values of ![]() , the solution maintains numerical stability.
, the solution maintains numerical stability.
Example 4
Consider the following nonlinear IVP:
![]()
with the initial condition ![]() . Find the values of
. Find the values of ![]() for
for ![]() taking
taking ![]() using the implicit Euler method.
using the implicit Euler method.
Solution
Using Mathematica, the exact solution to the differential equation given can be obtained as:
![]()
The implicit Euler scheme provides the following estimate for ![]() :
:
![]()
Since ![]() appears on both sides, and the equation is nonlinear in
appears on both sides, and the equation is nonlinear in ![]() , therefore, the Newton-Raphson method will be used at each time increment to find the value of
, therefore, the Newton-Raphson method will be used at each time increment to find the value of ![]() !
!
Setting ![]() ,
, ![]() ,
, ![]() , and
, and ![]() yields:
yields:
![]()
Solving the above nonlinear equation in ![]() using the Newton-Raphson method yields:
using the Newton-Raphson method yields:
![]()
Similarly, with ![]() , the equation for
, the equation for ![]() is:
is:
![]()
Using the Newton-Raphson method:
![]()
Proceeding iteratively produces the following table:
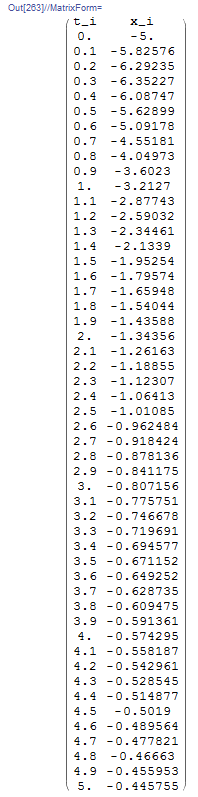
The following is the plot of the exact solution (blue line) with the data obtained using the implicit Euler method. The Mathematica code is given below.
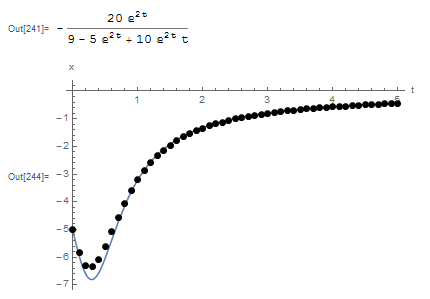 View Mathematica Code
View Mathematica CodeImplicitEulerMethod[fp_, x0_, h_, t0_, tmax_] :=
(n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[s = FindRoot[x == xtable[[i - 1]] + h*fp[x, t0 + (i - 1) h], {x, xtable[[i - 1]]}]; xtable[[i]] = x /. s[[1]], {i, 2, n}];
Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data2)
Clear[x, xtable]
a = DSolve[{x'[t] == t*x[t]^2 + 2*x[t], x[0] == -5}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := t*x^2 + 2*x;
Data2 = ImplicitEulerMethod[fp, -5.0, 0.1, 0, 5];
Plot[x, {t, 0, 5}, Epilog -> {PointSize[Large], Point[Data2]},AxesOrigin -> {0, 0}, AxesLabel -> {"t", "x"}, PlotRange -> All]
Title = {"t_i", "x_i"};
Data2 = Prepend[Data2, Title];
Data2 // MatrixForm
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
sp.init_printing(use_latex=True)
def ImplicitEulerMethod(fp, x0, h, t0, tmax):
n = int((tmax - t0)/h + 1)
xtable = [0 for i in range(n)]
xtable[0] = x0
x = sp.symbols('x')
for i in range(1,n):
s = sp.nsolve(x - xtable[i - 1] - h*fp(x, t0 + i*h), x, xtable[i - 1])
xtable[i] = s
Data = [[t0 + i*h, xtable[i]] for i in range(n)]
return Data
x = sp.Function('x')
t = sp.symbols('t')
sol = sp.dsolve(x(t).diff(t) - t*x(t)**2 - 2*x(t), ics={x(0): -5})
display(sol)
def fp(x, t): return t*x**2 + 2*x
Data = ImplicitEulerMethod(fp, -5.0, 0.1, 0, 5)
x_val = np.arange(0,5,0.01)
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.scatter([point[0] for point in Data],[point[1] for point in Data],c='k')
plt.xlabel("t"); plt.ylabel("x")
plt.grid(); plt.show()
print(["t_i", "x_i"],"\n",np.vstack(Data))

This was so helpful to me, thanks