Engineering at Alberta Courses

Numerical Integration: Rectangle Method

Rectangle Method

Let $f:[a,b]\rightarrow \mathbb{R}$ . The rectangle method utilizes the Riemann integral definition to calculate an approximate estimate for the area under the curve by drawing many rectangles with very small width adjacent to each other between the graph of the function $f$ and the $x$ axis. For simplicity, the width of the rectangles is chosen to be constant. Let $n$ be the number of intervals with $a=x_0 < x_1 < x_2 < \cdots < x_n=b$ and constant spacing $h=x_{i+1}-x_i$ . The rectangle method can be implemented in one of the following three ways:

$\begin{split}I_1&=\int_{a}^b\!f(x)\,\mathrm{d}x\approx h\sum_{i=1}^{n}f(x_{i-1})\\I_2&=\int_{a}^b\!f(x)\,\mathrm{d}x\approx h\sum_{i=1}^{n}f\left(\frac{x_{i-1}+x_{i}}{2}\right)\\I_3&=\int_{a}^b\!f(x)\,\mathrm{d}x\approx h\sum_{i=1}^{n}f(x_{i})\end{split}$

If $x_{i-1}$ and $x_{i}$ are the left and right points defining the rectangle number $i$ , then $I_1$ assumes that the height of the rectangle is equal to $f(x_{i-1})$ , $I_2$ assumes that the height of the rectangle is equal to $f\left(\frac{x_{i-1}+x_{i}}{2}\right)$ , and $I_3$ assumes that the height of the rectangle is equal to $f(x_{i})$ . $I_2$ is called the midpoint rule.
To illustrate the difference, consider the function $f(x)=x^2$ on the interval $[0,1]$ . The exact integral can be calculated as

$I_{\mbox{exact}}=\frac{x^3}{3}\bigg|_{x=0}^{x=1}=0.3333$

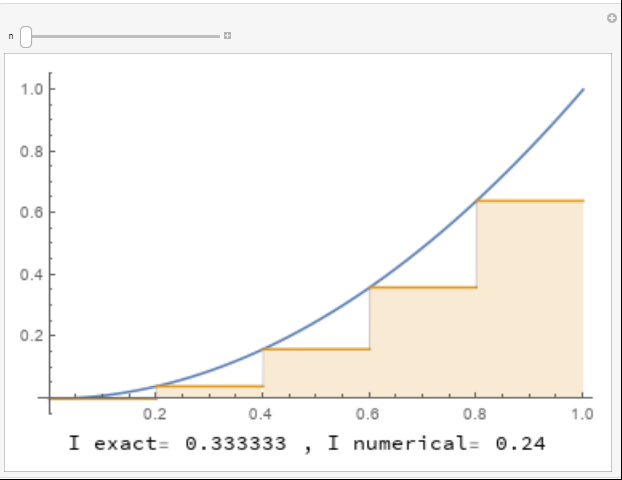
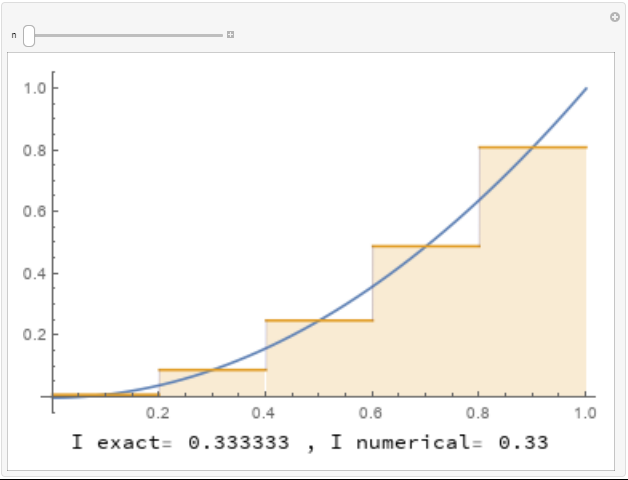
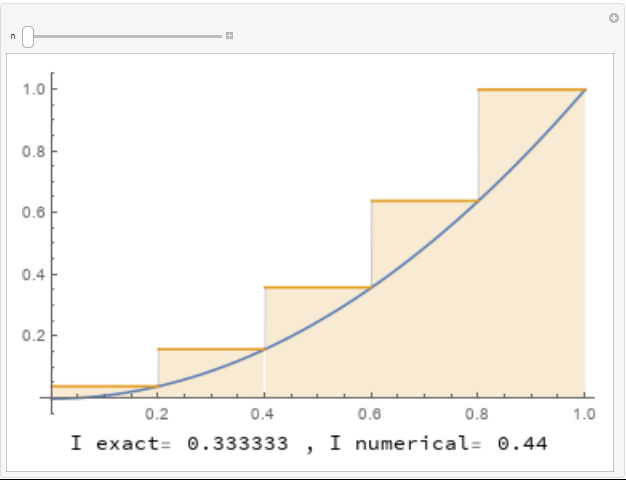
The following three tools show the implementation of the rectangle method for numerically integrating the function using $I_1$ , $I_2$ , and $I_3$ , respectively. For $I_1$ , each rectangle touches the graph of the function at the top left corner of the rectangle. For $I_2$ , each rectangle touches the graph of the function at the mid point of the top side. For $I_3$ , each rectangle touches the graph of the function at the top right corner of the rectangle. The areas of the rectangles are calculated underneath each curve. Use the slider to increase the number of rectangles to see how many rectangles are needed to get a good approximation for the area under the curve.

The following Mathematica code can be used to numerically integrate any function $f$ on the interval $[a,b]$ using the three options for the rectangle method.

View Mathematica Code

I1[f_, a_, b_, n_] := (h = (b - a)/n; Sum[f[a + (i - 1)*h]*h, {i, 1, n}])
I2[f_, a_, b_, n_] := (h = (b - a)/n; Sum[f[a + (i - 1/2)*h]*h, {i, 1, n}])
I3[f_, a_, b_, n_] := (h = (b - a)/n; Sum[f[a + (i)*h]*h, {i, 1, n}])
f[x_] := x^2;
I1[f, 0, 1, 13.0]
I2[f, 0, 1, 13.0]
I3[f, 0, 1, 13.0]

View Python Code

def I1(f, a, b, n):
  h = (b - a)/n
  return sum([f(a + i*h)*h for i in range(int(n))])
def I2(f, a, b, n):
  h = (b - a)/n
  return sum([f(a + (i + 1/2)*h)*h for i in range(int(n))])
def I3(f, a, b, n):
  h = (b - a)/n
  return sum([f(a + (i + 1)*h)*h for i in range(int(n))])
def f(x): return x**2
print("I1:",I1(f, 0, 1, 13.0))
print("I2:",I2(f, 0, 1, 13.0))
print("I3:",I3(f, 0, 1, 13.0))

The following link provides the MATLAB codes for implementing the rectangle method.

MATLAB files: File 1 (rect.m)

Error Analysis

Taylor’s theorem can be used to find how the error changes as the step size $h$ decreases. First, let’s consider $I_1$ (the same applies to $I_3$ ). The error in the calculation of rectangle number $i$ between the points $x_{i-1}$ and $x_{i}$ will be estimated. Using Taylor’s theorem, $\forall x\in[x_{i-1},x_{i}], \exists \xi\in[x_{i-1},x]$ such that:

$f(x)=f(x_{i-1})+f'(\xi)(x-x_{i-1})$

The error in the integral using this rectangle can be calculated as follows:

$\begin{split}|E_i|&=\left|\int_{x_{i-1}}^{x_{i}}\!f(x)-f(x_{i-1})\,\mathrm{d}x\right|=\left|\int_{x_{i-1}}^{x_{i}}\!f'(\xi)(x-x_{i-1})\,\mathrm{d}x\right|\\&\leq \max_{\xi\in[x_{i-1},x_i]}|f'(\xi)|\frac{(x-x_{i-1})^2}{2}\bigg|_{x_{i-1}}^{x_i}=\max_{\xi\in[x_{i-1},x_i]}|f'(\xi)|\frac{h^2}{2}\end{split}$

If $n$ is the number of subdivisions (number of rectangles), i.e., $nh=b-a$ , then:

$|E|=|nE_i| \leq \max_{\xi\in[a,b]}|f'(\xi)| n\frac{h^2}{2}=\max_{\xi\in[a,b]}|f'(\xi)| (b-a)\frac{h}{2}$

In other words, the total error is bounded by a term that is directly proportional to $h$ . When $h$ decreases, the error bound decreases proportionally. Of course when $h$ goes to zero, the error goes to zero as well.

$I_2$ (Midpoint rule) provides a faster convergence rate, or a more accurate approximation as the error is bounded by a term that is directly proportional to $h^2$ as will be shown here.
Using Taylor’s theorem, $\forall x\in[x_{i-1},x_{i}], \exists \xi\in[x_{i-1},x]$ such that:

$f(x)=f(x_{m})+f'(x_i)(x-x_{m})+f''(\xi)\frac{(x-x_{m})^2}{2}$

Where $x_m=\frac{x_{i-1}+x_{i}}{2}$ . The error in the integral using this rectangle can be calculated as follows:

$\begin{split}|E_i|&=\left|\int_{x_{i-1}}^{x_{i}}\!f(x)-f(x_m)\,\mathrm{d}x\right|=\left|f'(x_i)\int_{x_{i-1}}^{x_{i}}\!(x-x_m)\,\mathrm{d}x+\int_{x_{i-1}}^{x_{i}}\!\frac{f''(\xi)}{2}(x-x_m)^2\,\mathrm{d}x\right|\\&=\left|f'(x_i)\frac{(x_i-x_m)^2-(x_{i-1}-x_m)^2}{2}+\int_{x_{i-1}}^{x_{i}}\!\frac{f''(\xi)}{2}(x-x_m)^2\,\mathrm{d}x\right|\\&=\left|0+\int_{x_{i-1}}^{x_{i}}\!\frac{f''(\xi)}{2}(x-x_m)^2\,\mathrm{d}x\right|\\&\leq \max_{\xi\in[x_{i-1},x_i]}\frac{|f''(\xi)|}{2}\frac{\left(\frac{h}{2}\right)^3-\left(\frac{-h}{2}\right)^3}{3}\\&\leq \max_{\xi\in[x_{i-1},x_i]}\frac{|f''(\xi)|}{24}h^3\end{split}$

If $n$ is the number of subdivisions (number of rectangles), i.e., $nh=b-a$ , then:

$|E|=|nE_i| \leq \max_{\xi\in[a,b]}|f''(\xi)| n\frac{h^3}{24}=\max_{\xi\in[a,b]}|f''(\xi)| (b-a)\frac{h^2}{24}$

In other words, the total error is bounded by a term that is directly proportional to $h^2$ which provides faster convergence than $I_1$ . The tools shown above can provide a good illustration of this. With only five rectangles, $I_2$ already provides a very good estimate for the integral compared to both $I_1$ , and $I_3$ .

Example

Using the rectangle method with $n=4$ , calculate $I_1$ , $I_2$ , and $I_3$ and compare with the exact integral of the function $f(x)=e^x$ on the interval $[0,2]$ . Then, find the values of $h$ required so that the total error obtained by $I_1$ and that obtained by $I_2$ are bounded by 0.001.

Solution

Since $n=4$ the spacing $h$ can be calculated as:

$h=\frac{b-a}{n}=\frac{2-0}{4}=0.5$

Therefore, $x_0=0$ , $x_1=0.5$ , $x_2=1$ , $x_3=1.5$ , and $x_4=2.0$ . The values of the function at these points are given by:

$f(x_0)=e^0=1.00\qquad f(x_1)=e^{0.5}=1.6487 \qquad f(x_2)=e^{1}=2.7183$

$f(x_3)=e^{1.5}=4.4817 \qquad f(x_4)=e^{2}=7.3891$

According to the rectangle method we have:

$\begin{split}I_1&=\sum_{i=1}^{n}f(x_{i-1})h=0.5 (1 + 1.6487 + 2.7183 + 4.4817) = 4.924\\I_3&=\sum_{i=1}^{n}f(x_{i})h=0.5 (1.6487 + 2.7183 + 4.4817+7.3891) = 8.119\end{split}$

For $I_2$ , we need to calculate the values of the function at the midpoint of each rectangle:

$f\left(\frac{x_0+x_1}{2}\right)=e^{0.25}=1.284 \qquad f\left(\frac{x_1+x_2}{2}\right)=e^{0.75}=2.117$

$f\left(\frac{x_2+x_3}{2}\right)=e^{1.25}=3.49 \qquad f\left(\frac{x_3+x_4}{2}\right)=e^{1.75}=5.755$

Therefore:

$I_2=\sum_{i=1}^{n}f\left(\frac{x_{i-1}+x_{i}}{2}\right)h=0.5(1.284+2.117+3.49+5.755)=6.323$

The exact integral is given by:

$I=\int_{0}^2\!e^x\,\mathrm{d}x=e^2-e^0=6.38906$

Obviously, $I_2$ provides a good approximation with only 4 rectangles!

Error Bounds

The total errors obtained when $h=0.5$ are indeed less than the error bounds obtained by the formulas listed above. For $I_1$ and $I_3$ , the error in the estimation is bounded by:

$|E|\leq \max_{\xi\in[a,b]}|f'(\xi)| (b-a)\frac{h}{2}=e^{2}(2-0)\frac{0.5}{2}=3.695$

The errors $|I-I_1|=|6.38906-4.924|=1.4651$ and $|I-I_3|=|6.38906-8.119|=1.73$ are indeed less than that upper bound. The same formula can be used to find the value of $h$ so that the error is bounded by 0.001:

$e^{2}(2-0)\frac{h}{2}=0.001\Rightarrow h=0.000135$

Therefore, to guarantee an error less than 0.001 using $I_1$ , the interval will have to be divided into: $\frac{2}{0.000135}=14778$ rectangles! In this case $I_1=6.38862$ and $|E|=|6.38862-6.38906|=0.000432$

Similarly, when $h=0.5$ the error in the estimate using $I_2$ is bounded by:

$|E|=\max_{\xi\in[a,b]}|f''(\xi)| (b-a)\frac{h^2}{24}=e^2(2-0)\frac{0.5^2}{24}=0.1539$

The error $|I-I_2|=|6.38906-6.323|=0.06606$ is indeed bounded by that upper error. The same formula can be used to find the value of $h$ so that the error is bounded by 0.001:

$e^2(2-0)\frac{h^2}{24}=0.001\Rightarrow h = 0.04$

Therefore, to guarantee an error less than 0.001 using $I_2$ , the interval will have to be divided into: $\frac{2}{0.04}=50$ rectangles! In this case $I_2=6.38863$ and $|E|=|6.38863-6.38906|=0.000426$

Lecture Video

Page Comments

AM_Graduate says:

November 12, 2021 at 8:17 am

Thank you for uploading informative lectures.

I have a question about error analysis for I2 (midpoint rule).
In this lecture, using Taylor’s theorem, we expand up to three terms (including the remainder term) for I2 while up to two terms for I1 (and I3). Is there a specific reason for this?
(I guess it is because we use two points, x(i-1) and x(i), to calculate the midpoint, but still this does not sound plausible to me.)
I would appreciate it if you could explain this for me.

Again, thank you for uploading your wonderful lectures.

Reply
1. Samer Adeeb says:
  
  November 12, 2021 at 10:33 am
  
  Indeed, intuitively speaking, using the mid-point leads to a decrease in the associated error since there is tendency for positive and negative errors to cancel each other.
  When attempting to find a rigorous upper bound for the error, one starts with the Taylor approximation with as many terms as possible. For the I1 and I3, having more than two terms will not enable finding an upper bound. For I2, with three terms, it is possible to find an upper bound as per the derivation above.
  
  Reply
  1. AM_Graduate says:
    
    November 12, 2021 at 8:34 pm
    
    Thank you for your explanation. Now I can see it.

Open Educational Resources