Open Educational Resources

Numerical Integration: Gauss Quadrature

Gauss Quadrature

The Gauss integration scheme is a very efficient method to perform numerical integration over intervals. In fact, if the function to be integrated is a polynomial of an appropriate degree, then the Gauss integration scheme produces exact results. The Gauss integration scheme has been implemented in almost every finite element analysis software due to its simplicity and computational efficiency. This section outlines the basic principles behind the Gauss integration scheme. For its application to the finite element analysis method, please visit this section.

Introduction

Gauss quadrature aims to find the “least” number of fixed points to approximate the integral of a function f:[-1,1]\rightarrow \mathbb{R} such that:

    \[ I=\int_{-1}^{1} \! f\,\mathrm{d}x \approx \sum_{i=1}^n w_i f(x_i) \]

where \forall 1\leq i\leq n:x_i\in[-1,1] and w_i\in\mathbb{R}. Also, \forall i:x_i is called an integration point and w_i is called the associated weight. The number of integration points and the associated weights are chosen according to the complexity of the function f to be integrated. Since a general polynomial of degree 2n-1 has 2n coefficients, it is possible to find a Gauss integration scheme with n number of integration points and n number of associated weights to exactly integrate that polynomial function on the interval [-1,1]. The following figure illustrates the concept of using the Gauss integration points to calculate the area under the curve for polynomials. In the following sections, the required number of integration points for particular polynomials are presented.

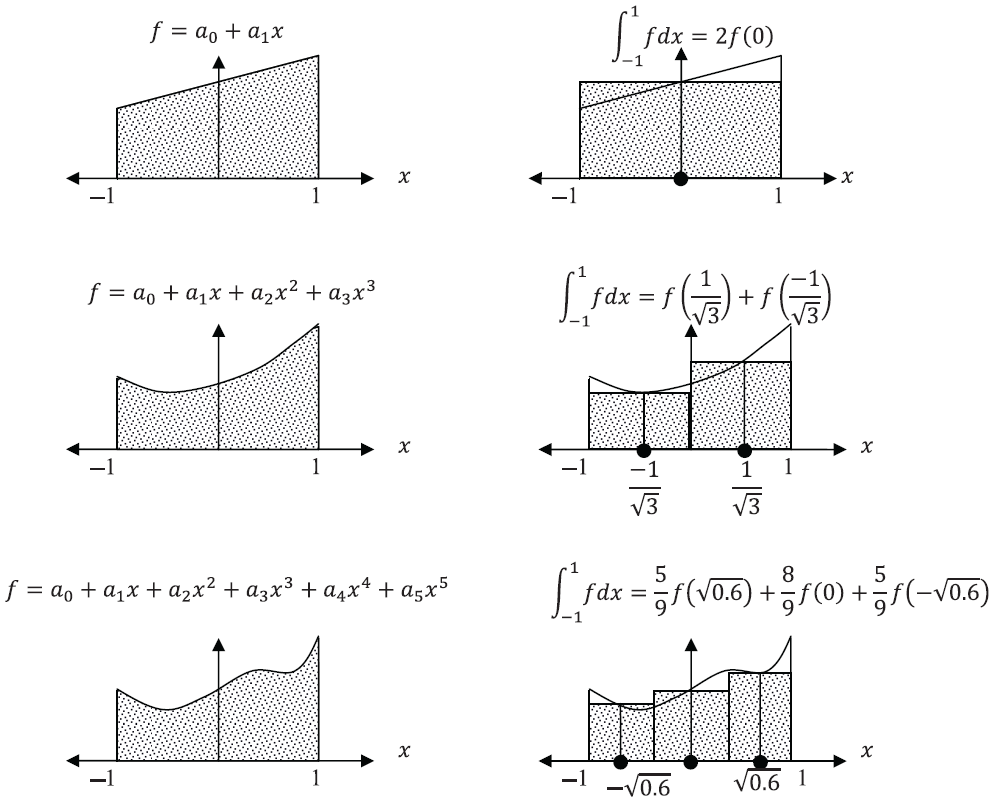
Gauss Integration for Polynomials of the 1st, 3rd and 5th Degrees

Gauss Integration for Polynomials of the 1st, 3rd and 5th Degrees

Affine Functions (First-Degree Polynomials): One Integration Point

For a first-degree polynomial, 2n-1=1, therefore, n=1, so, 1 integration point is sufficient as will be shown here. Consider f(x)=ax+b with a,b\in\mathbb{R}, then:

    \[ \int_{-1}^{1} \! ax+b\,\mathrm{d}x=2b+a\frac{x^2}{2}\bigg|_{-1}^1=2b=2f(0) \]

So, for functions that are very close to being affine, a numerical integration scheme with 1 integration point that is x_1=0 with an associated weight of 2 can be employed. In other words, a one-point numerical integration scheme has the form:

    \[ I=\int_{-1}^{1} \! f\,\mathrm{d}x \approx 2 f(0) \]

Third-Degree Polynomials: Two Integration Points

For a third-degree polynomial, 2n-1=3, therefore, n=2, so, 2 integration points are sufficient as will be shown here. Consider f(x)=a_0+a_1x+a_2x^2+a_3x^3, then:

    \[ \int_{-1}^{1} \! a_0+a_1x+a_2x^2+a_3x^3\,\mathrm{d}x=2a_0+2\frac{a_2}{3} \]

Assuming 2 integration points in the Gauss integration scheme yields:

    \[ \int_{-1}^{1} \! a_0+a_1x+a_2x^2+a_3x^3\,\mathrm{d}x=w_1(a_0+a_1x_1+a_2x_1^2+a_3x_1^3)+w_2(a_0+a_1x_2+a_2x_2^2+a_3x_2^3) \]

For the Gauss integration scheme to yield accurate results, the right-hand sides of the two equations above need to be equal for any choice of a cubic function. Therefore the multipliers of a_0, a_1, a_2, and a_3 should be the same. So, four equations in four unknowns can be written as follows:

    \[ \begin{split} w_1+w_2&=2\\ w_1x_1+w_2x_2&=0\\ w_1x_1^2+w_2x_2^2&=\frac{2}{3}\\ w_1x_1^3+w_2x_2^3&=0 \end{split} \]

The solution to the above four equations yields x_1=\frac{-1}{\sqrt{3}}, x_2=\frac{1}{\sqrt{3}}, w_1=w_2=1. The Mathematica code below forms the above equations and solves them:

View Mathematica Code
f = a0 + a1*x + a2*x^2 + a3*x^3;
I1 = Integrate[f, {x, -1, 1}]
I2 = w1*(f /. x -> x1) + w2*(f /. x -> x2)
Eq1 = Coefficient[I1 - I2, a0]
Eq2 = Coefficient[I1 - I2, a1]
Eq3 = Coefficient[I1 - I2, a2]
Eq4 = Coefficient[I1 - I2, a3]
Solve[{Eq1 == 0, Eq2 == 0, Eq3 == 0, Eq4 == 0}, {x1, x2, w1, w2}]
View Python Code
import sympy as sp
sp.init_printing(use_latex=True)
x, x1, x2 = sp.symbols('x x1 x2')
a0, a1, a2, a3 = sp.symbols('a0 a1 a2 a3')
w1, w2 = sp.symbols('w1 w2')
f = a0 + a1*x + a2*x**2 + a3*x**3
I1 = sp.integrate(f, (x, -1, 1))
I2 = w1*(f.subs(x, x1)) + w2*(f.subs(x, x2))
display("I1: ",I1)
display("I2: ",I2)
Eq1 = sp.expand(I1 - I2).coeff(a0)
Eq2 = sp.expand(I1 - I2).coeff(a1)
Eq3 = sp.expand(I1 - I2).coeff(a2)
Eq4 = sp.expand(I1 - I2).coeff(a3)
display("Eq1: ",Eq1)
display("Eq2: ",Eq2)
display("Eq3: ",Eq3)
display("Eq4: ",Eq4)
sol = list(sp.nonlinsolve([Eq1, Eq2, Eq3, Eq4], [x1, x2, w1, w2]))
display(sol)

So, for functions that are very close to being cubic, the following numerical integration scheme with 2 integration points can be employed:

    \[ I=\int_{-1}^{1} \! f\,\mathrm{d}x \approx f\left(\frac{-1}{\sqrt{3}}\right)+f\left(\frac{1}{\sqrt{3}}\right) \]

Fifth-Degree Polynomials: Three Integration Points

For a fifth-degree polynomial, 2n-1=5, therefore, n=3, so, 3 integration points are sufficient to exactly integrate a fifth-degree polynomial. Consider f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5, then:

    \[ \int_{-1}^{1} \! a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5\,\mathrm{d}x=2a_0+2\frac{a_2}{3}+2\frac{a_4}{5} \]

Assuming 3 integration points in the Gauss integration scheme yields:

    \[\begin{split} \int_{-1}^{1} \! &a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5\,\mathrm{d}x=w_1(a_0+a_1x_1+a_2x_1^2+a_3x_1^3+a_4x_1^4+a_5x_1^5)\\ &+w_2(a_0+a_1x_2+a_2x_2^2+a_3x_2^3+a_4x_2^4+a_5x_2^5)+w_3(a_0+a_1x_3+a_2x_3^2+a_3x_3^3+a_4x_3^4+a_5x_3^5) \end{split} \]

For the Gauss integration scheme to yield accurate results, the right-hand sides of the two equations above need to be equal for any choice of a fifth-order polynomial function. Therefore the multipliers of a_0, a_1, a_2, a_3, a_4, and a_5 should be the same. So, six equations in six unknowns can be written as follows:

    \[ \begin{split} w_1+w_2+w_3&=2\\ w_1x_1+w_2x_2+w_3x_3&=0\\ w_1x_1^2+w_2x_2^2+w_3x_3^2&=\frac{2}{3}\\ w_1x_1^3+w_2x_2^3+w_3x_3^3&=0\\ w_1x_1^4+w_2x_2^4+w_3x_3^4&=\frac{2}{5}\\ w_1x_1^5+w_2x_2^5+w_3x_3^5&=0 \end{split} \]

The solution to the above six equations yields x_1=-\sqrt{\frac{3}{5}}, x_2=0, x_3=\sqrt{\frac{3}{5}}, w_1=\frac{5}{9}, w_2=\frac{8}{9}, and w_3=\frac{5}{9}. The Mathematica code below forms the above equations and solves them:

View Mathematica Code
f = a0 + a1*x + a2*x^2 + a3*x^3 + a4*x^4 + a5*x^5;
I1 = Integrate[f, {x, -1, 1}]
I2 = w1*(f /. x -> x1) + w2*(f /. x -> x2) + w3*(f /. x -> x3)
Eq1 = Coefficient[I1 - I2, a0]
Eq2 = Coefficient[I1 - I2, a1]
Eq3 = Coefficient[I1 - I2, a2]
Eq4 = Coefficient[I1 - I2, a3]
Eq5 = Coefficient[I1 - I2, a4]
Eq6 = Coefficient[I1 - I2, a5]
Solve[{Eq1 == 0, Eq2 == 0, Eq3 == 0, Eq4 == 0, Eq5 == 0, Eq6 == 0}, {x1, x2, x3, w1, w2, w3}]
View Python Code
import sympy as sp
sp.init_printing(use_latex=True)
x, x1, x2, x3 = sp.symbols('x x1 x2 x3')
a0, a1, a2, a3, a4, a5 = sp.symbols('a0 a1 a2 a3 a4 a5')
w1, w2, w3 = sp.symbols('w1 w2 w3')
f = a0 + a1*x + a2*x**2 + a3*x**3 + a4*x**4 + a5*x**5
I1 = sp.integrate(f, (x, -1, 1))
I2 = w1*(f.subs(x, x1)) + w2*(f.subs(x, x2)) + w3*(f.subs(x, x3))
display("I1: ",I1)
display("I2: ",I2)
Eq1 = sp.expand(I1 - I2).coeff(a0)
Eq2 = sp.expand(I1 - I2).coeff(a1)
Eq3 = sp.expand(I1 - I2).coeff(a2)
Eq4 = sp.expand(I1 - I2).coeff(a3)
Eq5 = sp.expand(I1 - I2).coeff(a4)
Eq6 = sp.expand(I1 - I2).coeff(a5)
display("Eq1: ",Eq1)
display("Eq2: ",Eq2)
display("Eq3: ",Eq3)
display("Eq4: ",Eq4)
display("Eq5: ",Eq5)
display("Eq6: ",Eq6)
sol = list(sp.nonlinsolve([Eq1, Eq2, Eq3, Eq4, Eq5, Eq6], [x1, x2, x3, w1, w2, w3]))
display(sol)

So, for functions that are very close to being fifth-order polynomials, the following numerical integration scheme with 3 integration points can be employed:

    \[ I=\int_{-1}^{1} \! f\,\mathrm{d}x \approx \frac{5}{9}f\left(-\sqrt{\frac{3}{5}}\right)+\frac{8}{9}f(0)+\frac{5}{9}f\left(\sqrt{\frac{3}{5}}\right) \]

Seventh-Degree Polynomial: Four Integration Points

For a seventh-degree polynomial, 2n-1=7, therefore, n=4, so, 4 integration points are sufficient to exactly integrate a seventh-degree polynomial. Following the procedure outlined above, the integration points along with the associated weight:

    \[\begin{split} x_1=-0.861136 \qquad w_1=0.347855\\ x_2=-0.339981 \qquad w_2=0.652145\\ x_3=0.339981 \qquad w_3=0.652145\\ x_4=0.861136 \qquad w_4=0.347855 \end{split} \]

So, for functions that are very close to being seventh-order polynomials, the following numerical integration scheme with 4 integration points can be employed:

    \[\begin{split} I&=\int_{-1}^{1} \! f\,\mathrm{d}x\\ & \approx 0.347855f(-0.861136)+0.652145f(-0.339981)\\ & +0.652145f(0.339981)+0.347855f(0.861136) \end{split} \]

The following is the Mathematica code used to find the above integration points and corresponding weights.

View Mathematica Code
f = a0 + a1*x + a2*x^2 + a3*x^3 + a4*x^4 + a5*x^5 + a6*x^6 + a7*x^7;
I1 = Integrate[f, {x, -1, 1}]
I2 = w1*(f /. x -> x1) + w2*(f /. x -> x2) + w3*(f /. x -> x3) +  w4*(f /. x -> x4)
Eq1 = Coefficient[I1 - I2, a0]
Eq2 = Coefficient[I1 - I2, a1]
Eq3 = Coefficient[I1 - I2, a2]
Eq4 = Coefficient[I1 - I2, a3]
Eq5 = Coefficient[I1 - I2, a4]
Eq6 = Coefficient[I1 - I2, a5]
Eq7 = Coefficient[I1 - I2, a6]
Eq8 = Coefficient[I1 - I2, a7]
a = Solve[{Eq1 == 0, Eq2 == 0, Eq3 == 0, Eq4 == 0, Eq5 == 0, Eq6 == 0,  Eq7 == 0, Eq8 == 0}, {x1, x2, x3, w1, w2, w3, x4, w4}]
Chop[N[a[[1]]]]
View Python Code
import sympy as sp
sp.init_printing(use_latex=True)
x, x1, x2, x3, x4 = sp.symbols('x x1 x2 x3 x4')
a0, a1, a2, a3, a4, a5, a6, a7 = sp.symbols('a0 a1 a2 a3 a4 a5 a6 a7')
w1, w2, w3, w4 = sp.symbols('w1 w2 w3 w4')
f = a0 + a1*x + a2*x**2 + a3*x**3 + a4*x**4 + a5*x**5 + a6*x**6 + a7*x**7
I1 = sp.integrate(f, (x, -1, 1)).subs({x3:-x1,x4:-x2,w3:w1,w4:w2})
I2 = (w1*(f.subs(x, x1)) + w2*(f.subs(x, x2)) + w3*(f.subs(x, x3)) +  w4*(f.subs(x, x4))).subs({x3:-x1,x4:-x2,w3:w1,w4:w2})
display("I1: ",I1)
display("I2: ",I2)
Eq1 = sp.expand(I1 - I2).coeff(a0)
Eq2 = sp.expand(I1 - I2).coeff(a1)
Eq3 = sp.expand(I1 - I2).coeff(a2)
Eq4 = sp.expand(I1 - I2).coeff(a3)
Eq5 = sp.expand(I1 - I2).coeff(a4)
Eq6 = sp.expand(I1 - I2).coeff(a5)
Eq7 = sp.expand(I1 - I2).coeff(a6)
Eq8 = sp.expand(I1 - I2).coeff(a7)
display("Eq1: ",Eq1)
display("Eq2: ",Eq2)
display("Eq3: ",Eq3)
display("Eq4: ",Eq4)
display("Eq5: ",Eq5)
display("Eq6: ",Eq6)
display("Eq7: ",Eq7)
display("Eq8: ",Eq8)
sol = list(sp.nonlinsolve([Eq1, Eq3, Eq5, Eq7], [x1, x2, w1, w2]))
display(sol)

Ninth-Degree Polynomial: Five Integration Points

For a ninth-degree polynomial, 2n-1=9, therefore, n=5, so, 5 integration points are sufficient to exactly integrate a ninth-degree polynomial. Following the procedure outlined above, the integration points along with the associated weight:

    \[\begin{split} x_1=-0.90618 \qquad w_1=0.236927\\ x_2=-0.538469 \qquad w_2=0.478629\\ x_3=0 \qquad w_3=0.568889\\ x_4=0.538469 \qquad w_4=0.478629\\ x_5=0.90618 \qquad w_5=0.236927 \end{split} \]

So, for functions that are very close to being ninth-order polynomials, the following numerical integration scheme with 5 integration points can be employed:

    \[\begin{split} I&=\int_{-1}^{1} \! f\,\mathrm{d}x\\ & \approx 0.236927f(-0.90618)+0.478629f(-0.538469)\\ & +0.568889f(0)+0.478629f(0.538469)\\ & + 0.236927 f(0.90618) \end{split} \]

The following is the Mathematica code used to find the above integration points and corresponding weights.

View Mathematica Code
f = a0 + a1*x + a2*x^2 + a3*x^3 + a4*x^4 + a5*x^5 + a6*x^6 + a7*x^7 +  a8*x^8 + a9*x^9;
I1 = Integrate[f, {x, -1, 1}]
I2 = w1*(f /. x -> x1) + w2*(f /. x -> x2) + w3*(f /. x -> x3) +   w4*(f /. x -> x4) + w5*(f /. x -> x5)
Eq1 = Coefficient[I1 - I2, a0]
Eq2 = Coefficient[I1 - I2, a1]
Eq3 = Coefficient[I1 - I2, a2]
Eq4 = Coefficient[I1 - I2, a3]
Eq5 = Coefficient[I1 - I2, a4]
Eq6 = Coefficient[I1 - I2, a5]
Eq7 = Coefficient[I1 - I2, a6]
Eq8 = Coefficient[I1 - I2, a7]

Eq9 = Coefficient[I1 - I2, a8]
Eq10 = Coefficient[I1 - I2, a9]

a = Solve[{Eq1 == 0, Eq2 == 0, Eq3 == 0, Eq4 == 0, Eq5 == 0, Eq6 == 0,  Eq7 == 0, Eq8 == 0, Eq9 == 0, Eq10 == 0}, {x1, x2, x3, w1, w2, w3, x4, w4, x5, w5}]
Chop[N[a[[1]]]]
View Python Code
import sympy as sp
sp.init_printing(use_latex=True)
x, x1, x2, x3, x4, x5 = sp.symbols('x x1 x2 x3 x4 x5')
a0, a1, a2, a3, a4, a5, a6, a7, a8, a9 = sp.symbols('a0 a1 a2 a3 a4 a5 a6 a7 a8 a9')
w1, w2, w3, w4, w5 = sp.symbols('w1 w2 w3 w4 w5')
f = a0 + a1*x + a2*x**2 + a3*x**3 + a4*x**4 + a5*x**5 + a6*x**6 + a7*x**7 + a8*x**8 + a9*x**9
I1 = sp.integrate(f, (x, -1, 1)).subs({x3:-x1,x4:-x2,x5:0,w3:w1,w4:w2})
I2 = (w1*(f.subs(x, x1)) + w2*(f.subs(x, x2)) + w3*(f.subs(x, x3)) +   w4*(f.subs(x, x4)) + w5*(f.subs(x, x5))).subs({x3:-x1,x4:-x2,x5:0,w3:w1,w4:w2})
display("I1: ",I1)
display("I2: ",I2)
Eq1 = sp.expand(I1 - I2).coeff(a0)
Eq2 = sp.expand(I1 - I2).coeff(a1)
Eq3 = sp.expand(I1 - I2).coeff(a2)
Eq4 = sp.expand(I1 - I2).coeff(a3)
Eq5 = sp.expand(I1 - I2).coeff(a4)
Eq6 = sp.expand(I1 - I2).coeff(a5)
Eq7 = sp.expand(I1 - I2).coeff(a6)
Eq8 = sp.expand(I1 - I2).coeff(a7)
Eq9 = sp.expand(I1 - I2).coeff(a8)
Eq10 = sp.expand(I1 - I2).coeff(a9)
display("Eq1: ",Eq1)
display("Eq2: ",Eq2)
display("Eq3: ",Eq3)
display("Eq4: ",Eq4)
display("Eq5: ",Eq5)
display("Eq6: ",Eq6)
display("Eq7: ",Eq7)
display("Eq8: ",Eq8)
display("Eq9: ",Eq9)
display("Eq10: ",Eq10)
sol = list(sp.nonlinsolve([Eq1, Eq3, Eq5, Eq7, Eq9], [x1, x2, w1, w2, w5]))
display(sol)

Eleventh-Degree Polynomial: Six Integration Points

For an eleventh-degree polynomial, 2n-1=11, therefore, n=6, so, 6 integration points are sufficient to exactly integrate an eleventh-degree polynomial. Following the procedure outlined above, the integration points along with the associated weight:

    \[\begin{split} x_1=-0.93247 \qquad w_1=0.171324\\ x_2=-0.661209 \qquad w_2=0.360762\\ x_3=-0.238619 \qquad w_3=0.467914\\ x_4=0.238619 \qquad w_4=0.467914\\ x_5=0.661209 \qquad w_5=0.360762\\ x_6=0.93247 \qquad w_6=0.171324\\ \end{split} \]

So, for functions that are very close to being eleventh-order polynomials, the following numerical integration scheme with 6 integration points can be employed:

    \[\begin{split} I&=\int_{-1}^{1} \! f\,\mathrm{d}x\\ & \approx 0.171324f(-0.93247 )+0.360762f(-0.661209 )\\ & +0.467914f(-0.238619)+0.467914f(0.238619)\\ & + 0.360762f(0.661209 )+0.171324f(0.93247 ) \end{split} \]

The following is the Mathematica code used to find the above integration points and corresponding weights. Note that symmetry was employed to reduce the number of equations.

View Mathematica Code
f = a0 + a1*x + a2*x^2 + a3*x^3 + a4*x^4 + a5*x^5 + a6*x^6 + a7*x^7 + a8*x^8 + a9*x^9 + a10*x^10 + a11*x^11;
I1 = Integrate[f, {x, -1, 1}]
I2 =  w1*(f /. x -> x1) + w2*(f /. x -> x2) + w3*(f /. x -> x3) + 
   w3*(f /. x -> -x3) + w2*(f /. x -> -x2) + w1*(f /. x -> -x1)
Eq1 = Coefficient[I1 - I2, a0]
Eq3 = Coefficient[I1 - I2, a2]
Eq5 = Coefficient[I1 - I2, a4]
Eq7 = Coefficient[I1 - I2, a6]
Eq9 = Coefficient[I1 - I2, a8]
Eq11 = Coefficient[I1 - I2, a10]
a = Solve[{Eq1 == 0, Eq3 == 0, Eq5 == 0, Eq7 == 0, Eq9 == 0, Eq11 == 0}, {x1, x2, x3, w1, w2, w3}]
Chop[N[a[[1]]]]
View Python Code
import numpy as np
import sympy as sp
from scipy.optimize import fsolve
sp.init_printing(use_latex=True)

x, x1, x2, x3 = sp.symbols('x x1 x2 x3')
a0, a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11 = sp.symbols('a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11')
w1, w2, w3, w4, w5 = sp.symbols('w1 w2 w3 w4 w5')
f = a0 + a1*x + a2*x**2 + a3*x**3 + a4*x**4 + a5*x**5 + a6*x**6 + a7*x**7 + a8*x**8 + a9*x**9 + a10*x**10 + a11*x**11
I1 = sp.integrate(f, (x, -1, 1))
I2 =  w1*(f.subs(x, x1)) + w2*(f.subs(x, x2)) + w3*(f.subs(x, x3)) + w3*(f.subs(x, -x3)) + w2*(f.subs(x, -x2)) + w1*(f.subs(x, -x1))
display("I1: ",I1)
display("I2: ",I2)
Eq1 = sp.expand(I1 - I2).coeff(a0)
Eq2 = sp.expand(I1 - I2).coeff(a1)
Eq3 = sp.expand(I1 - I2).coeff(a2)
Eq4 = sp.expand(I1 - I2).coeff(a3)
Eq5 = sp.expand(I1 - I2).coeff(a4)
Eq6 = sp.expand(I1 - I2).coeff(a5)
Eq7 = sp.expand(I1 - I2).coeff(a6)
Eq8 = sp.expand(I1 - I2).coeff(a7)
Eq9 = sp.expand(I1 - I2).coeff(a8)
Eq10 = sp.expand(I1 - I2).coeff(a9)
Eq11 = sp.expand(I1 - I2).coeff(a10)
display("Eq1: ",Eq1)
display("Eq2: ",Eq2)
display("Eq3: ",Eq3)
display("Eq4: ",Eq4)
display("Eq5: ",Eq5)
display("Eq6: ",Eq6)
display("Eq7: ",Eq7)
display("Eq8: ",Eq8)
display("Eq9: ",Eq9)
display("Eq10: ",Eq10)
display("Eq11: ",Eq11)

# Convert Sympy equations to a Python function using lambdify
Equations = sp.lambdify(([x1, x2, x3, w1, w2, w3],), [Eq1, Eq3, Eq5, Eq7, Eq9, Eq11])
# Solve system of equations using Scipy's fsolve
sol = fsolve(Equations, [-0.5,-1,-0.3,0,0,0])
display(sol)

We can continue determining more integration points (abscissae) and weights for Gauss quadrature. In this page, the integration points and weights up to 64 points are available. Note that 64 integration points of Gauss quadrature is associated with a polynomial of degree 127.

Implementation of Gauss Quadrature

Gauss quadrature is very easy to implement and provides very accurate results with very few computations. However, one drawback is that it is not applicable to data obtained experimentally as the values of the function at the specific integration points would not be necessarily available. In order to implement the Gauss integration scheme in Mathematica, first, the following table is created which contains the integration points and the corresponding weights. Row number i contains the Gauss integration scheme with i-1 integration points. Then, a procedure is created in Mathematica whose input is a function f, and the requested number of integration points. The procedure then calls the appropriate row in the “GaussTable” and calculates the weighted sum of the function evaluated at the appropriate integration points.
GuassPoints

View Mathematica Code
Clear[f, x]
GaussTable = {{{"Integration Points"}, {"Corresponding Weights"}}, {{0}, {2}}, {{-1/Sqrt[3], 1/Sqrt[3]}, {1, 1}}, {{-Sqrt[3/5], 0, Sqrt[3/5]}, {5/9, 8/9, 5/9}}, {{-0.861136, -0.339981, 0.339981, 0.861136}, {0.347855, 0.652145, 0.652145, 0.347855}}, {{-0.90618, -0.538469, 0, 0.538469, 0.90618}, {0.236927, 0.478629, 0.568889, 0.478629, 0.236927}}, {{-0.93247, -0.661209, -0.238619, 0.238619, 0.661209, 0.93247}, {0.171324, 0.360762, 0.467914, 0.467914, 0.360762,  0.171324}}};
GaussTable // MatrixForm
IG[f_, n_] := Sum[GaussTable[[n + 1, 2, i]]*f[GaussTable[[n + 1, 1, i]]], {i, 1, n}]
f[x_] := x^9 + x^8
IG[f, 5.0]
View Python Code
import numpy as np
import pandas as pd
GaussTable = [[[0], [2]], [[-1/np.sqrt(3), 1/np.sqrt(3)], [1, 1]], [[-np.sqrt(3/5), 0, np.sqrt(3/5)], [5/9, 8/9, 5/9]], [[-0.861136, -0.339981, 0.339981, 0.861136], [0.347855, 0.652145, 0.652145, 0.347855]], [[-0.90618, -0.538469, 0, 0.538469, 0.90618], [0.236927, 0.478629, 0.568889, 0.478629, 0.236927]], [[-0.93247, -0.661209, -0.238619, 0.238619, 0.661209, 0.93247], [0.171324, 0.360762, 0.467914, 0.467914, 0.360762,  0.171324]]]
display(pd.DataFrame(GaussTable, columns=["Integration Points", "Corresponding Weights"]))
def IG(f, n):
  n = int(n)
  return sum([GaussTable[n - 1][1][i]*f(GaussTable[n - 1][0][i]) for i in range(n)])
def f(x): return x**9 + x**8
IG(f, 5.0)
Example

Calculate the exact integral of \cos{x} on the interval [-1,1] and find the relative error if a Gauss 1, 2, 3, and 4 integration points scheme is used. Also, calculate the number of rectangles required by the midpoint rule of the rectangle method to produce an error similar to that produced by the 3 point integration scheme, then evaluate the integral using the midpoint rule of the rectangle method with the obtained number of rectangles.

Solution

The exact integral is given by:

    \[ I=\int_{-1}^{1}\!\cos{x}\,\mathrm{d}x=\sin{(1)}-\sin{(-1)}=1.68294 \]

Employing a Gauss integration scheme with one integration point yields:

    \[\begin{split} I_1&=w_1\cos{x_1}=2 \cos{(0)}=2\\ E_r&=\frac{1.68294-2}{1.68294}=-0.1884 \end{split} \]

Employing a Gauss integration scheme with two integration points yields:

    \[ \begin{split} I_2&=w_1\cos{x_1}+w_2\cos{x_2}=\cos{\left(\frac{-1}{\sqrt{3}}\right)}+\cos{\left(\frac{1}{\sqrt{3}}\right)}=1.67582\\ E_r&=\frac{1.68294-1.67582}{1.68294}=0.00422968 \end{split} \]

Employing a Gauss integration scheme with three integration points yields:

    \[\begin{split} I_3&=w_1\cos{x_1}+w_2\cos{x_2}+w_3\cos{x_3}=\frac{5}{9}\cos{\left(-\sqrt{\frac{3}{5}}\right)}+\frac{8}{9}\cos{(0)}+\frac{5}{9}\cos{\left(\sqrt{\frac{3}{5}}\right)}=1.683\\ E_r&=\frac{1.68294-1.683}{1.68294}=-0.0003659 \end{split} \]

Employing a Gauss integration scheme with four integration points yields:

    \[\begin{split} I_4&=w_1\cos{x_1}+w_2\cos{x_2}+w_3\cos{x_3}+w_4\cos{x_4}\\ &= 0.347855\cos(-0.861136)+0.652145\cos(-0.339981)\\ &+0.652145\cos(0.339981)+0.347855\cos(0.861136)\\ &=1.68294\\ E_r&=\frac{1.68294-1.68294}{1.68294}=0 \end{split} \]

Using a three point integration scheme yielded an error of:

    \[ |E|=|1.68294-1.683| = |-0.00006|=0.00006 \]

Equating the upper bound for the error in the midpoint rule to the error produced by a three-point Gauss integration scheme yields:

    \[ \max_{\xi\in[a,b]}|f''(\xi)| (b-a)\frac{h^2}{24}=0.00006 \]

With b-a=1-(-1)=2, and \max_{\xi\in[a,b]}|f''(\xi)|=1. Therefore:

    \[ h=\sqrt{\frac{0.00006\times 24}{2}}=0.02683 \]

Therefore, the required number of rectangles is:

    \[ n=\frac{b-a}{h}=\frac{2}{0.02683}\approx 75 \]

With 75 rectangles the rectangle method yields an integral of I_{\mbox{rectangle}}=1.68299. It is important to note how accurate the Gauss integration scheme is compared to the rectangle method. For this example, it would take 75 divisions (equivalent to 75 integration points) to reach an accuracy similar to the Gauss integration scheme with only 3 points!

View Mathematica Code
Clear[f, x, I2]
GaussTable = {{{"Integration Points"}, {"Corresponding Weights"}}, {{0}, {2}}, {{-1/Sqrt[3], 1/Sqrt[3]}, {1, 1}}, {{-Sqrt[3/5], 0,  Sqrt[3/5]}, {5/9, 8/9, 5/9}}, {{-0.861136, -0.339981, 0.339981, 0.861136}, {0.347855, 0.652145, 0.652145, 0.347855}}, {{-0.90618, -0.538469, 0, 0.538469, 0.90618}, {0.236927, 0.478629, 0.568889, 0.478629, 0.236927}}, {{-0.93247, -0.661209, -0.238619, 0.238619, 0.661209, 0.93247}, {0.171324, 0.360762, 0.467914, 0.467914, 0.360762,  0.171324}}};
GaussTable // MatrixForm
IG[f_, n_] := Sum[GaussTable[[n + 1, 2, i]]*f[GaussTable[[n + 1, 1, i]]], {i, 1,  n}];
f[x_] := Cos[x]
Iexact = Integrate[Cos[x], {x, -1, 1.0}]
Itable = Table[{i, N[IG[f, i]], (Iexact - IG[f, i])/Iexact}, {i, 1, 6}];
Title = {"Number of Integration Points",  "Numerical Integration Results", "Relative Error"};
Itable = Prepend[Itable, Title];
Itable // MatrixForm
h = Sqrt[0.00006*24/2/1]
n = Ceiling[2/h]
I2[f_, a_, b_, n_] := (h = (b - a)/n; Sum[f[a + (i - 1/2)*h]*h, {i, 1, n}])
I2[f, -1.0, 1, n]
View Python Code
import numpy as np
import sympy as sp
import pandas as pd
from scipy import integrate

GaussTable = [[[0], [2]], [[-1/np.sqrt(3), 1/np.sqrt(3)], [1, 1]], [[-np.sqrt(3/5), 0, np.sqrt(3/5)], [5/9, 8/9, 5/9]], [[-0.861136, -0.339981, 0.339981, 0.861136], [0.347855, 0.652145, 0.652145, 0.347855]], [[-0.90618, -0.538469, 0, 0.538469, 0.90618], [0.236927, 0.478629, 0.568889, 0.478629, 0.236927]], [[-0.93247, -0.661209, -0.238619, 0.238619, 0.661209, 0.93247], [0.171324, 0.360762, 0.467914, 0.467914, 0.360762,  0.171324]]]
display(pd.DataFrame(GaussTable, columns=["Integration Points", "Corresponding Weights"]))
def IG(f, n):
  n = int(n)
  return sum([GaussTable[n - 1][1][i]*f(GaussTable[n - 1][0][i]) for i in range(n)])
def f(x): return np.cos(x)
Iexact, error = integrate.quad(f, -1, 1)
print("Iexact: ",Iexact)
Itable = [[i + 1, sp.N(IG(f, i + 1)), (Iexact - IG(f, i + 1))/Iexact] for i in range(6)]
Itable = pd.DataFrame(Itable, columns=["Number of Integration Points",  "Numerical Integration Results", "Relative Error"])
display(Itable)
h = np.sqrt(0.00006*24/2/1)
print("h: ",h)
n = np.ceil(2/h)
print("n: ",n)
def I2(f, a, b, n):
  h = (b - a)/n
  return sum([f(a + (i + 1/2)*h)*h for i in range(int(n))])
I2(f, -1.0, 1, n)
MATLAB files: File 1 (ex11_8.m)File 2 (gauss_quad.m)
Alternate Integration Limits

The Gauss integration scheme presented above applies to functions that are integrated over the interval [-1,1]. A simple change of variables can be used to allow integrating a function g(z) where z\in[a,b]. In this case, the linear relationship between z and x can be expressed as:

    \[ \frac{z-a}{b-a}=\frac{x-(-1)}{1-(-1)}=\frac{x+1}{2} \]

Therefore:

    \[ \mathrm{d}z=\frac{(b-a)}{2}\mathrm{d}x \]

Which means the integration can be converted from integrating over z to integrating over x as follows:

    \[ \int_{a}^b\! g(z)\,\mathrm{d}z=\int_{-1}^1\! g(z(x))\,\frac{(b-a)}{2}\mathrm{d}x \]

where

    \[ z(x)=\frac{(b-a)(x+1)}{2}+a=\frac{(b-a)(x)+(b+a)}{2} \]

Therefore:

    \[ \int_{a}^b\! g(z)\,\mathrm{d}z=\int_{-1}^1\! g\left(\frac{(b-a)(x)+(b+a)}{2}\right)\,\frac{(b-a)}{2}\mathrm{d}x \]

The integration can then proceed as per the weights and values of the integration points with f(x) given by:

    \[ f(x)=g\left(\frac{(b-a)(x)+(b+a)}{2}\right)\,\frac{(b-a)}{2} \]

Example

Calculate the exact integral of xe^x on the interval [0,3] and find the absolute relative error if a Gauss 1, 2, 3, and 4 integration points scheme is used.

Solution

First, to differentiate between the given function limits, and the limits after changing variables, we will assume that the function is given in terms of z as follows:

    \[ g(z)=ze^z \]

The exact integral is given by:

    \[ \int_{0}^3\!ze^z\,\mathrm{d}z=e^z(z-1)|_{z=0}^{z=3}=2e^3+1=41.1711 \]

Using a linear change of variables z=z(x) we have:

    \[ \int_{a}^b\! g(z)\,\mathrm{d}z=\int_{-1}^1\! g\left(\frac{(b-a)(x)+(b+a)}{2}\right)\,\frac{(b-a)}{2}\mathrm{d}x \]

Therefore:

    \[ \int_{0}^3\! ze^z\,\mathrm{d}z=\int_{-1}^1\! g\left(\frac{3x+3}{2}\right)\frac{3}{2}\,\mathrm{d}x=\int_{-1}^1\! \left(\frac{(3x+3)}{2}\right)e^{\left(\frac{(3x+3)}{2}\right)}\frac{3}{2}\,\mathrm{d}x \]

Employing a Gauss integration scheme with one integration point yields:

    \[\begin{split} I_1&=w_1f(x_1)=2 f(0)=2 \left(\frac{(3(0)+3)}{2}\right)e^{\left(\frac{(3(0)+3)}{2}\right)}\frac{3}{2}=20.1676\\ E_r&=\frac{41.1711-20.1676}{41.1711}=0.51 \end{split} \]

Employing a Gauss integration scheme with two integration points yields:

    \[ \begin{split} I_2&=w_1f(x_1)+w_2f(x_2)\\ &=\left(\frac{(3\left(-\sqrt{\frac{1}{3}}\right)+3)}{2}\right)e^{\left(\frac{(3\left(-\sqrt{\frac{1}{3}}\right)+3)}{2}\right)}\frac{3}{2}+\left(\frac{(3\left(\sqrt{\frac{1}{3}}\right)+3)}{2}\right)e^{\left(\frac{(3\left(\sqrt{\frac{1}{3}}\right)+3)}{2}\right)}\frac{3}{2}=39.607\\ E_r&=\frac{41.1711-39.607}{41.1711}=0.038 \end{split} \]

Employing a Gauss integration scheme with three integration points yields:

    \[\begin{split} I_3&=w_1f(x_1)+w_2f(x_2)+w_3f(x_3)=\frac{5}{9}f(x_1)+\frac{8}{9}f(x_2)+\frac{5}{9}f(x_3)=41.1313\\ E_r&=\frac{41.1711-41.1313}{41.1711}=0.0009657 \end{split} \]

where,

    \[\begin{split} f(x_1)&=f(-\sqrt{0.6})=\left(\frac{(3(-\sqrt{0.6})+3)}{2}\right)e^{\left(\frac{(3(-\sqrt{0.6})+3)}{2}\right)}\frac{3}{2}\\ f(x_2)&=f(0)=\left(\frac{(3(0)+3)}{2}\right)e^{\left(\frac{(3(0)+3)}{2}\right)}\frac{3}{2}\\ f(x_3)&=f(\sqrt{0.6})=\left(\frac{(3(\sqrt{0.6})+3)}{2}\right)e^{\left(\frac{(3(\sqrt{0.6})+3)}{2}\right)}\frac{3}{2} \end{split} \]

In the following Mathematica code, the procedure IGAL applies the Gauss integration scheme with n integration points to a function f on the interval [a,b]

View Mathematica Code
GaussTable = {{{"Integration Points"}, {"Corresponding Weights"}}, {{0}, {2}}, {{-1/Sqrt[3], 1/Sqrt[3]}, {1, 1}}, {{-Sqrt[3/5], 0,  Sqrt[3/5]}, {5/9, 8/9, 5/9}}, {{-0.861136, -0.339981, 0.339981,  0.861136}, {0.347855, 0.652145, 0.652145,  0.347855}}, {{-0.90618, -0.538469, 0, 0.538469, 0.90618}, {0.236927, 0.478629, 0.568889, 0.478629,  0.236927}}, {{-0.93247, -0.661209, -0.238619, 0.238619, 0.661209,      0.93247}, {0.171324, 0.360762, 0.467914, 0.467914, 0.360762,      0.171324}}};
GaussTable // MatrixForm
IGAL[f_, n_, a_, b_] := Sum[(b - a)/2*GaussTable[[n + 1, 2, i]]*f[(b - a)/2*(GaussTable[[n + 1, 1, i]] + 1) + a], {i, 1, n}]
f[x_] := x*E^x
Iexact = Integrate[f[x], {x, 0., 3}]
Itable = Table[{i, N[IGAL[f, i, 0, 3]], (Iexact - IGAL[f, i, 0, 3])/Iexact}, {i, 1, 6}];
Title = {"Number of Integration Points",  "Numerical Integration Results", "Relative Error"};
Itable = Prepend[Itable, Title];
Itable // MatrixForm
View Python Code
import numpy as np
import sympy as sp
import pandas as pd
from scipy import integrate

GaussTable = [[[0], [2]], [[-1/np.sqrt(3), 1/np.sqrt(3)], [1, 1]], [[-np.sqrt(3/5), 0, np.sqrt(3/5)], [5/9, 8/9, 5/9]], [[-0.861136, -0.339981, 0.339981, 0.861136], [0.347855, 0.652145, 0.652145, 0.347855]], [[-0.90618, -0.538469, 0, 0.538469, 0.90618], [0.236927, 0.478629, 0.568889, 0.478629, 0.236927]], [[-0.93247, -0.661209, -0.238619, 0.238619, 0.661209, 0.93247], [0.171324, 0.360762, 0.467914, 0.467914, 0.360762,  0.171324]]]
display(pd.DataFrame(GaussTable, columns=["Integration Points", "Corresponding Weights"]))
def IGAL(f, n, a, b):
  n = int(n)
  return sum([(b - a)/2*GaussTable[n - 1][1][i]*f((b - a)/2*(GaussTable[n - 1][0][i] + 1) + a) for i in range(n)])
def f(x): return x*np.exp(x)
Iexact, error = integrate.quad(f, 0, 3)
print("Iexact: ",Iexact)
Itable = [[i + 1, sp.N(IGAL(f, i + 1, 0, 3)), (Iexact - IGAL(f, i + 1, 0, 3))/Iexact] for i in range(6)]
Itable = pd.DataFrame(Itable, columns=["Number of Integration Points",  "Numerical Integration Results", "Relative Error"])
display(Itable)
MATLAB files: File 1 (ex11_9.m) File 2 (gauss_quad.m)

Lecture Video


Page Comments

  1. Nick says:
    April 13, 2022 at 1:27 pm

    Hello! Very helpful article! I do have one question though. For the python code, what if I would like to solve a double integral? As an example, what if I have r^2*cos(theta)drdtheta and I would like to integrate in terms of both r and theta (from 0 to 1 and 0 to pi respectively)? I do see how one can do this in the Mathematica version (likely due to my greater experience using Mathematica) but I keep running into issues attempting this in Python. Any help would be greatly appreciated

    Reply
    1. Samer Adeeb says:
      April 13, 2022 at 1:32 pm

      You can post your code here (or email it to me) and I can take a look.
      It should be straightforward in any language. You can review the following page:
      https://engcourses-uofa.ca/books/introduction-to-solid-mechanics/finite-element-analysis/one-and-two-dimensional-isoparametric-elements-and-gauss-integration/gauss-integration/#gauss-integration-over-two-dimensional-domains-6

      Reply
      1. Nick says:
        April 13, 2022 at 2:32 pm

        Here is the code I came up with. I’m assuming one of the problems is how I define “theta” (if you run “ampf” it’s clear that the function is not actually integrating in terms of theta). I have slowly learned that defining variables in python is a bit more involved than mathematica!

        import numpy as np
        from matplotlib import pyplot as plt
        import matplotlib as mpl
        import sympy as sp
        from mpmath import *
        import pandas as pd
        from scipy import integrate
        GaussTable = [[[0], [2]], [[-1/np.sqrt(3), 1/np.sqrt(3)], [1, 1]], [[-np.sqrt(3/5), 0, np.sqrt(3/5)], [5/9, 8/9, 5/9]], [[-0.861136, -0.339981, 0.339981, 0.861136], [0.347855, 0.652145, 0.652145, 0.347855]], [[-0.90618, -0.538469, 0, 0.538469, 0.90618], [0.236927, 0.478629, 0.568889, 0.478629, 0.236927]], [[-0.93247, -0.661209, -0.238619, 0.238619, 0.661209, 0.93247], [0.171324, 0.360762, 0.467914, 0.467914, 0.360762, 0.171324]]]
        display(pd.DataFrame(GaussTable, columns=[“Integration Points”, “Corresponding Weights”]))
        def IG(f, n):
        n = int(n)
        return sum([GaussTable[n – 1][1][i]*f(GaussTable[n – 1][0][i]) for i in range(n)])
        theta = sp.symbols(“theta”)
        def f(r): return r**2*sp.cos(theta)
        n = 200
        def I2(f, a, b, n):
        h = (b – a)/n
        return sum([f(a + (i + 1/2)*h)*h for i in range(int(n))])
        ampr=I2(f, 0, 1, n)
        def g(theta): return ampr
        def I2(g, a, b, n):
        h = (b – a)/n
        return sum([g(a + (i + 1/2)*h)*h for i in range(int(n))])
        ampf=I2(g,0,3.14159265358,n)

  2. Samer Adeeb says:
    April 14, 2022 at 12:55 pm

    The integration function should look different. Please check this app that I created for this:
    https://mecsimcalc.com/app/0505681/gauss_integration

    You can find the code under: “app doc”. It seems to work properly up to th2=1.0Pi. I tried th2=2.0Pi and it didn’t give the expected output and I might have made a mistake. If you find a mistake, let me know.

    Reply
    1. Nick says:
      April 14, 2022 at 10:05 pm

      Thanks for the code! I played around with it and got something that seems to mostly work. The only issue I have found is that I get an error when n1 and n2 are greater than 6. Not fully sure why this is the case. For the example I give below n1=n2=6 is fine but I imagine I would need more steps for more complicated integrals. Any thoughts?
      import numpy as np
      from matplotlib import pyplot as plt
      import matplotlib as mpl
      import sympy as sp
      from mpmath import *
      import pandas as pd
      from scipy import integrate
      GaussTable = [[[0], [2]], [[-1/np.sqrt(3), 1/np.sqrt(3)], [1, 1]], [[-np.sqrt(3/5), 0, np.sqrt(3/5)], [5/9, 8/9, 5/9]], [[-0.861136, -0.339981, 0.339981, 0.861136], [0.347855, 0.652145, 0.652145, 0.347855]], [[-0.90618, -0.538469, 0, 0.538469, 0.90618], [0.236927, 0.478629, 0.568889, 0.478629, 0.236927]], [[-0.93247, -0.661209, -0.238619, 0.238619, 0.661209, 0.93247], [0.171324, 0.360762, 0.467914, 0.467914, 0.360762, 0.171324]]]
      display(pd.DataFrame(GaussTable, columns=[“Integration Points”, “Corresponding Weights”]))
      def IGAL(f, n1, r1, r2, n2,th1,th2):
      n1 = int(n1)
      n2 = int(n2)
      return sum([sum([(r2 – r1)/2*GaussTable[n1 – 1][1][i]*(th2 – th1)/2*GaussTable[n2 – 1][1][j]*f((r2 – r1)/2*(GaussTable[n1 – 1][0][i] + 1) + r1,(th2 – th1)/2*(GaussTable[n2 – 1][0][j] + 1) + th1) for i in range(n1)]) for j in range(n2)])
      def f(r,th):
      return r**2*np.sin(th)
      n1 = 6
      n2 = 6
      ampf=IGAL(f,n1,0,1,n2,0,np.pi)
      print(ampf)

      Reply
      1. Samer Adeeb says:
        April 14, 2022 at 10:11 pm

        The Gauss Table data provided in the code is only up to n=6

      2. Nick says:
        April 15, 2022 at 10:31 am

        Ohhh I see! Looks like I’m going to have to figure out how to calculate a much larger Gauss Table going forward. For the integration I plan to do, I may likely need n=200! (*not a factorial I’m just excited haha!)

Leave a Reply

Your email address will not be published.