Nonlinear Systems of Equations: Linear vs. Nonlinear Analysis
Linear vs. Nonlinear Analysis of Structures: An Application
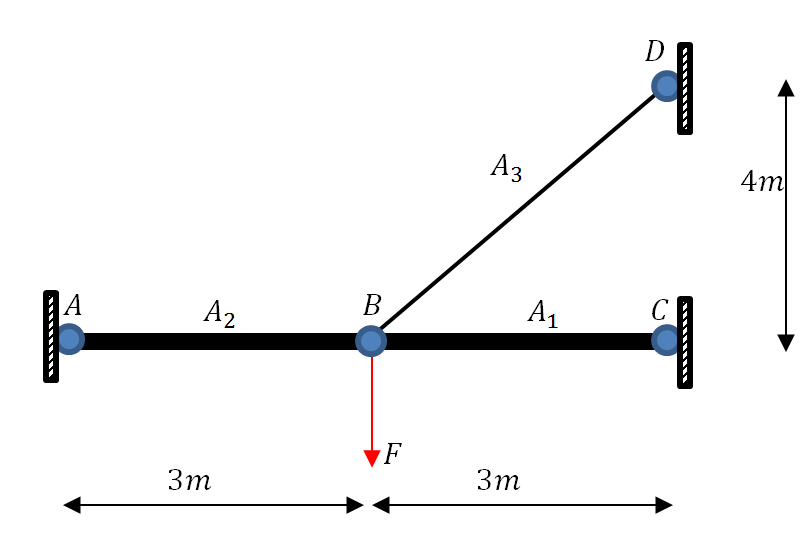
Most structural engineering problems in which the displacements and forces inside a structure are sought can be formulated using linear systems of equations. This is done by invoking certain assumptions that simplify the problem. However, when a structure undergoes large deformations, the problem has to be formulated using nonlinear systems of equations. The following is an example of a truss structure that aims at clarifying the difference.
Example
Two steel truss members with areas ![]() and
and ![]() are connected to a steel cable with an area
are connected to a steel cable with an area ![]() as shown in the figure. All the connections are hinged connections allowing free relative rotations. Points
as shown in the figure. All the connections are hinged connections allowing free relative rotations. Points ![]() ,
, ![]() , and
, and ![]() are fixed by means of hinges preventing displacements but allowing free rotations. Assuming that the horizontal displacement of point
are fixed by means of hinges preventing displacements but allowing free rotations. Assuming that the horizontal displacement of point ![]() is
is ![]() to the right and the vertical displacement of point
to the right and the vertical displacement of point ![]() is
is ![]() downwards. Assume that Young’s modulus
downwards. Assume that Young’s modulus ![]() ,
, ![]() , and
, and ![]() . The force in each member is equal to
. The force in each member is equal to ![]() where
where ![]() where
where ![]() is the member number,
is the member number, ![]() is the undeformed length,
is the undeformed length, ![]() is the deformed length,
is the deformed length, ![]() is the longitudinal stress,
is the longitudinal stress, ![]() is the strain, and
is the strain, and ![]() is Young’s modulus in member
is Young’s modulus in member ![]() . Find the values of
. Find the values of ![]() and
and ![]() at equilibrium using: 1) Linear analysis where the displacements are assumed to be small, and 2) Nonlinear analysis. Solve twice, once with
at equilibrium using: 1) Linear analysis where the displacements are assumed to be small, and 2) Nonlinear analysis. Solve twice, once with ![]() , and another time with
, and another time with ![]() . Do the two solution strategies give the same answer?
. Do the two solution strategies give the same answer?
Solution
The units adopted will be ![]() for forces,
for forces, ![]() for lengths, and
for lengths, and ![]() for
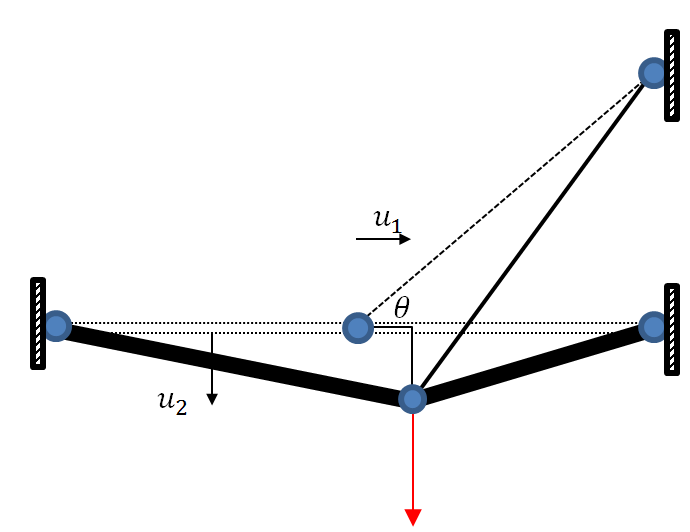
for ![]() . The following is the displaced shape of the structure. The middle hinge move horizontally to the right a distance
. The following is the displaced shape of the structure. The middle hinge move horizontally to the right a distance ![]() and vertically downards a distance
and vertically downards a distance ![]() . There are two unknowns in the problem
. There are two unknowns in the problem ![]() and
and ![]() . These can be found using two equations of equilibrium at the middle hinge. The two equations are the sum of the vertical and horizontal forces, each equal to zero.
. These can be found using two equations of equilibrium at the middle hinge. The two equations are the sum of the vertical and horizontal forces, each equal to zero.
Linear Analysis
In linear analysis, the truss member length is assumed to only change due to displacements along its longitudinal axis. In other words, the forces in the truss member do not change if it simply rotates. In addition, the forces are assumed to be aligned with the original geometry of the structure before deformations. The strains in each member are given by: ![]() ,
, ![]() , and
, and ![]() . Therefore, the forces in each member can be calculated as follows:
. Therefore, the forces in each member can be calculated as follows:
![Rendered by QuickLaTeX.com \[ \begin{split} F_1&=E_1A_1\varepsilon_1=E\left(\frac{200}{1000000}\right)\frac{-u_1}{3}\\ F_2&=E_2A_2\varepsilon_2=E\left(\frac{200}{1000000}\right)\frac{u_1}{3}\\ F_3&=E_3A_3\varepsilon_3=E\left(\frac{50}{1000000}\right)\frac{u_2\sin{(\theta)}-u_1\cos{(\theta)}}{5} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fd39fcbc13056b5f73bdd6069e8a9d0d_l3.png)
where ![]() ,
, ![]() , and
, and ![]() . Assuming small deformations, equilibrium at point
. Assuming small deformations, equilibrium at point ![]() can be analyzed using the following forces diagram:
can be analyzed using the following forces diagram:
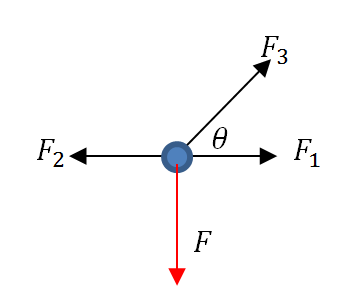
The first equation is the sum of horizontal forces equals to zero:
![]()
The second equation is the sum of the vertical forces equal to zero:
![]()
These equations are linear and can be written in matrix form as follows:
![]()
Setting ![]() yields a solution
yields a solution ![]() and
and ![]() , while setting
, while setting ![]() yields
yields ![]() and
and ![]() . Notice that in a linear analysis, the displacements are directly proportional to the applied load, that is, the ratio between
. Notice that in a linear analysis, the displacements are directly proportional to the applied load, that is, the ratio between ![]() at
at ![]() and
and ![]() at
at ![]() is equal to
is equal to ![]() . The same applies to
. The same applies to ![]() .
.
The following is the Mathematica code to formulate and solve the above system of equations using the “Solve” function.
View Mathematica CodeClear[F, Ee];
Ee = 200 (10^9);
eps1 = -u1/3;
A1 = A2 = 200/1000000;
A3 = 50/1000000;
eps2 = u1/3;
Cth = 3/5;
Sth = 4/5;
eps3 = (-u1*Cth + u2*Sth)/5;
F1 = Ee*A1*eps1;
F2 = Ee*A2*eps2;
F3 = Ee*A3*eps3;
Eq1 = Expand[(F1 + F3*Cth - F2)]
Eq2 = Expand[F - F3*Sth]
sol1 = Solve[{Eq1 == 0.0, Eq2 == 0.0 /. F -> 10000}]
sol2 = Solve[{Eq1 == 0.0, Eq2 == 0.0 /. F -> 500000}]
import sympy as sp
sp.init_printing(use_latex=True)
u1, u2, F = sp.symbols('u1 u2 F')
Ee = 200*(10**9)
eps1 = -u1/3
A1 = A2 = 200/1000000
A3 = 50/1000000
eps2 = u1/3
Cth = 3/5
Sth = 4/5
eps3 = (-u1*Cth + u2*Sth)/5
F1 = Ee*A1*eps1
F2 = Ee*A2*eps2
F3 = Ee*A3*eps3
Eq1 = F1 + F3*Cth - F2
Eq2 = F - F3*Sth
display("Eq1: ",Eq1)
display("Eq2: ",Eq2)
# Using Sympy's built-in linear solve function
display("sol1: ",sp.linsolve((Eq1, Eq2.subs({'F':10000})),(u1, u2)))
display("sol2: ",sp.linsolve((Eq1, Eq2.subs({'F':500000})),(u1, u2)))
Nonlinear Analysis
In a nonlinear analysis, the analysis takes into consideration the displaced position of the structure without any simplified assumptions. Looking at the first truss member, the displaced structure is shown in the following figure.
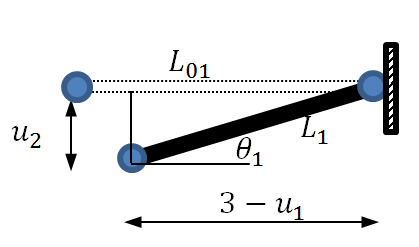
For this member, the original length ![]() , the final length
, the final length ![]() , the strain
, the strain ![]() and the angle of inclination
and the angle of inclination ![]() is such that
is such that ![]() and
and ![]() .
.
For the second truss member, the displaced structure is shown in the following figure.
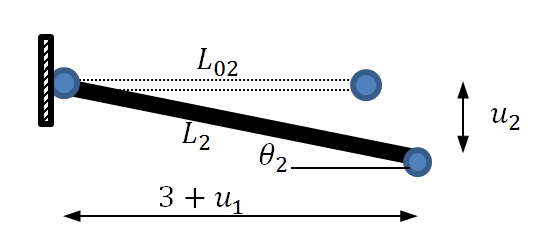
For this member, the original length ![]() , the final length
, the final length ![]() , the strain
, the strain ![]() and the angle of inclination
and the angle of inclination ![]() is such that
is such that ![]() and
and ![]() .
.
For the third truss member, the displaced structure is shown in the following figure.
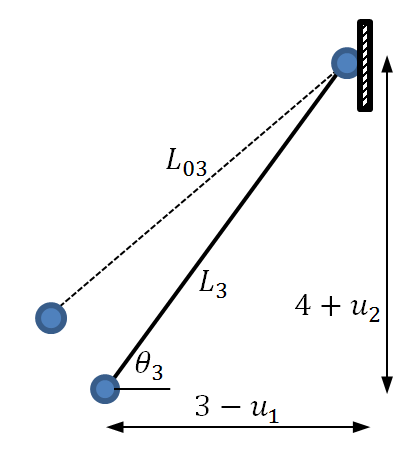
For this member, the original length ![]() , the final length
, the final length ![]() , the strain
, the strain ![]() and the angle of inclination
and the angle of inclination ![]() is such that
is such that ![]() and
and ![]() .
.
Finally, the equations of equilibrium can be written taking into consideration the inclination of each member:
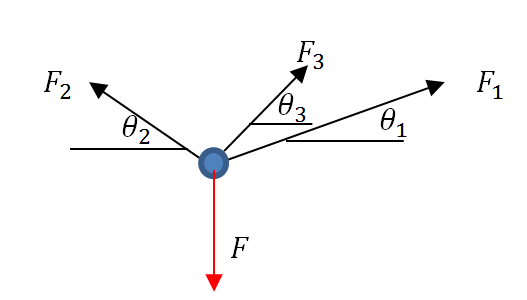
The first equation is the sum of horizontal forces equals to zero:
![]()
The second equation is the sum of the vertical forces equal to zero:
![]()
The following is a screenshot of the Mathematica output of the two equations:
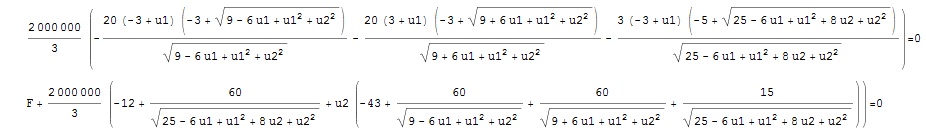
Setting ![]() yields a solution
yields a solution ![]() and
and ![]() , while setting
, while setting ![]() yields
yields ![]() and
and ![]() . For small deformations under small applied loads, the linear analysis and nonlinear analysis produce exactly the same results. In this situation, the rotations of the members are very small such that the original shape and the deformed shape can be assumed to be the same. However, under large loads, the linear analysis is no longer valid. The two solutions at
. For small deformations under small applied loads, the linear analysis and nonlinear analysis produce exactly the same results. In this situation, the rotations of the members are very small such that the original shape and the deformed shape can be assumed to be the same. However, under large loads, the linear analysis is no longer valid. The two solutions at ![]() are far from each other with the nonlinear analysis solution giving less displacement. In this particular situation, as the structure deforms, the nonlinear effects cause the structure to be more rigid and therefore exhibit less deformations. Cable structures with large loads and large deformations in the cables need to be analyzed using a nonlinear analysis rather than a linear analysis.
are far from each other with the nonlinear analysis solution giving less displacement. In this particular situation, as the structure deforms, the nonlinear effects cause the structure to be more rigid and therefore exhibit less deformations. Cable structures with large loads and large deformations in the cables need to be analyzed using a nonlinear analysis rather than a linear analysis.
The following is the Mathematica code to formulate and solve the above nonlinear system of equations using the “FindRoot” function with an initial guess of ![]() , and
, and ![]() .
.
Ee = 200 (10^9);
A1 = A2 = 200/1000000;
A3 = 50/1000000;
L1 = Sqrt[(3 - u1)^2 + u2^2];
Sth1 = u2/L1;
Cth1 = (3 - u1)/L1;
L2 = Sqrt[(3 + u1)^2 + u2^2];
Sth2 = u2/L2;
Cth2 = (3 + u1)/L2;
L3 = Sqrt[(3 - u1)^2 + (4 + u2)^2];
Cth3 = (3 - u1)/L3;
Sth3 = (4 + u2)/L3;
eps1 = (L1 - 3)/3;
eps2 = (L2 - 3)/3;
eps3 = (L3 - 5)/5;
F1 = Ee*A1*eps1;
F2 = Ee*A2*eps2;
F3 = Ee*A3*eps3;
Eq1 = Simplify[F1*Cth1 - F2*Cth2 + F3*Cth3]
Eq2 = Simplify[F - F1*Sth1 - F2*Sth2 - F3*Sth3]
sol1 = FindRoot[{Eq1 == 0, Eq2 == 0 /. F -> 10000}, {{u1, 0}, {u2, 0}}]
sol2 = FindRoot[{Eq1 == 0, Eq2 == 0 /. F -> 500000}, {{u1, 0}, {u2, 0}}]
import sympy as sp
sp.init_printing(use_latex=True)
u1, u2, F = sp.symbols('u1 u2 F')
Ee = 200*(10**9)
A1 = A2 = 200/1000000
A3 = 50/1000000
L1 = sp.sqrt((3 - u1)**2 + u2**2)
Sth1 = u2/L1
Cth1 = (3 - u1)/L1
L2 = sp.sqrt((3 + u1)**2 + u2**2)
Sth2 = u2/L2
Cth2 = (3 + u1)/L2
L3 = sp.sqrt((3 - u1)**2 + (4 + u2)**2)
Cth3 = (3 - u1)/L3
Sth3 = (4 + u2)/L3
eps1 = (L1 - 3)/3
eps2 = (L2 - 3)/3
eps3 = (L3 - 5)/5
F1 = Ee*A1*eps1
F2 = Ee*A2*eps2
F3 = Ee*A3*eps3
Eq1 = F1*Cth1 - F2*Cth2 + F3*Cth3
Eq2 = F - F1*Sth1 - F2*Sth2 - F3*Sth3
display("Eq1: ",Eq1)
display("Eq2: ",Eq2)
# Using Sympy's built-in nonlinear solve function
display("sol1: ",sp.nsolve((Eq1, Eq2.subs({'F':10000})), (u1,u2), (0,0)))
display("sol2: ",sp.nsolve((Eq1, Eq2.subs({'F':500000})), (u1,u2), (0,0)))

At the end of linear analysis,
“the ratio between u1 at F=10,000 and u1 at F=500,000 is equal to 500,000/10,000.”
It should be
“the ratio between u1 at F=10,000 and u1 at F=500,000 is equal to 10,000/500,000.”
Corrected! Thank you!