Solution Methods for IVPs: Runge-Kutta Methods
Runge-Kutta Methods
The Runge-Kutta methods developed by the German mathematicians C. Runge and M.W. Kutta are essentially a generalization of all the previous methods. Consider the following IVP:
![]()
Assuming that the value of the dependent variable
![]()
where
![]()
![Rendered by QuickLaTeX.com \[\begin{split}k_1&=F(x_i,t_i)\\k_2&=F(x_i+q_{11}k_1h,t_i+p_1h)\\k_3&=F(x_i+q_{21}k_1h+q_{22}k_2h,t_i+p_2h)\\&\vdots\\k_n&=F(x_i+q_{(n-1),1}k_1h+q_{(n-1),2}k_2h+\cdots+q_{(n-1),(n-1)}k_{n-1}h,t_i+p_{n-1}h)\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c1314f63af476961f92b4fb0afe0c0ad_l3.png)
The constants ![]() , and the forms of
, and the forms of ![]() are obtained by equating the value of
are obtained by equating the value of ![]() obtained using the Runge-Kutta equation to a particular form of the Taylor series. The
obtained using the Runge-Kutta equation to a particular form of the Taylor series. The ![]() are recurrence relationships, meaning
are recurrence relationships, meaning ![]() appears in
appears in ![]() , which appears in
, which appears in ![]() , and so forth. This makes the method efficient for computer calculations. The error in a particular form depends on how many terms are used. The general forms of these Runge-Kutta methods could be implicit or explicit. For example, the explicit Euler method is a Runge-Kutta method with only one term with
, and so forth. This makes the method efficient for computer calculations. The error in a particular form depends on how many terms are used. The general forms of these Runge-Kutta methods could be implicit or explicit. For example, the explicit Euler method is a Runge-Kutta method with only one term with ![]() and
and ![]() . Heun’s method on the other hand is a Runge-Kutta method with the following non-zero terms:
. Heun’s method on the other hand is a Runge-Kutta method with the following non-zero terms:
![Rendered by QuickLaTeX.com \[\begin{split}\alpha_1&=\alpha_2=\frac{1}{2}\\k_1&=F(x_i,t_i)\\k_2&=F(x_i+hk_1,t_i+h)\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-66dd07fb0d9f54a06ef391b4a3898dfb_l3.png)
Similarly, the midpoint method is a Runge-Kutta method with the following non-zero terms:
![Rendered by QuickLaTeX.com \[\begin{split}\alpha_2&=1\\k_1&=F(x_i,t_i)\\k_2&=F(x_i+\frac{h}{2}k_1,t_i+\frac{h}{2})\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e74d9aa59ceca8ae7777afece6b83fac_l3.png)
The most popular Runge-Kutta method is referred to as the “classical Runge-Kutta method”, or the “fourth-order Runge-Kutta method”. It has the following form:
![]()
with
![Rendered by QuickLaTeX.com \[\begin{split}k_1&=F(x_i,t_i)\\k_2&=F\left(x_i+\frac{h}{2}k_1,t_i+\frac{h}{2}\right)\\k_3&=F\left(x_i+\frac{h}{2}k_2,t_i+\frac{h}{2}\right)\\k_4&=F(x_i+hk_3,t_i+h)\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3c8365f0bbaf7ce0be1e9944f8e2f674_l3.png)
The error in the fourth-order Runge-Kutta method is similar to that of the Simpson’s 1/3 rule, with a local error term
RK4Method[fp_, x0_, h_, t0_, tmax_] := (n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[k1 = fp[xtable[[i - 1]], t0 + (i - 2) h];
k2 = fp[xtable[[i - 1]] + h/2*k1, t0 + (i - 1.5) h];
k3 = fp[xtable[[i - 1]] + h/2*k2, t0 + (i - 1.5) h];
k4 = fp[xtable[[i - 1]] + h*k3, t0 + (i - 1) h];
xtable[[i]] = xtable[[i - 1]] + h (k1 + 2 k2 + 2 k3 + k4)/6, {i, 2,
n}];
Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data2)
View Python Code
def RK4Method(fp, x0, h, t0, tmax):
n = int((tmax - t0)/h + 1)
xtable = [0 for i in range(n)]
xtable[0] = x0
for i in range(1,n):
k1 = fp(xtable[i - 1], t0 + (i - 1)*h)
k2 = fp(xtable[i - 1] + h/2*k1, t0 + (i - 0.5)*h)
k3 = fp(xtable[i - 1] + h/2*k2, t0 + (i - 0.5)*h)
k4 = fp(xtable[i - 1] + h*k3, t0 + i*h)
xtable[i] = xtable[i - 1] + h*(k1 + 2*k2 + 2*k3 + k4)/6
Data = [[t0 + i*h, xtable[i]] for i in range(n)]
return Data
Example
Solve Example 4 above using the classical Runge-Kutta method but with ![]() .
.
Solution
Recall the differential equation of this problem:
![]()
Setting
![Rendered by QuickLaTeX.com \[\begin{split}k_1&=F(x_0,t_0)=F(-5,0)\\&=0+2(-5)=-10\\k_2&=F\left(x_0+\frac{h}{2}k_1,t_0+\frac{h}{2}\right)=F(-5+0.2(-10),0+0.2)\\&=0.2(-5+0.2(-10))^2+2\times (-5+0.2(-10))=-4.2\\k_3&=F\left(x_0+\frac{h}{2}k_2,t_0+\frac{h}{2}\right)=F(-5+0.2(-4.2),0+0.2)\\&=0.2(-5+0.2(-4.2))^2+2\times (-5+0.2(-4.2))=-4.8589\\k_4&=F(x_0+hk_3,t_0+h)=F(-5+0.4(-4.8589),0+0.4)\\&=0.4(-5+0.4(-4.8589))^2+2\times(-5+0.4(-4.8589))=5.3981\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f3d532d527b557ce7bb152e293f3ba47_l3.png)
Therefore:
![]()
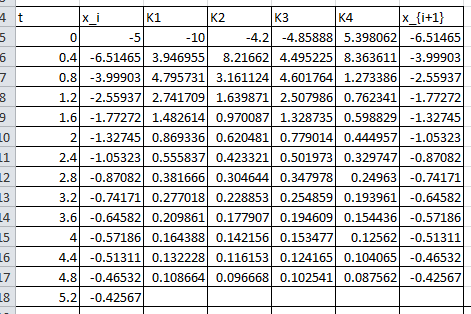
Proceeding iteratively gives the values of ![]() up to
up to ![]() . The Microsoft Excel file RK4.xlsx provides the required calculations. The following Microsoft Excel table shows the required calculations:
. The Microsoft Excel file RK4.xlsx provides the required calculations. The following Microsoft Excel table shows the required calculations:
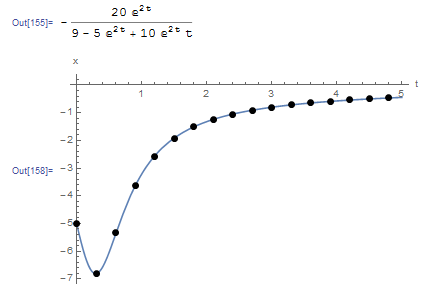
The following Mathematica code implements the classical Runge-Kutta method for this problem with ![]() . The output curve is shown underneath.
. The output curve is shown underneath.
RK4Method[fp_, x0_, h_, t0_, tmax_] := (n = (tmax - t0)/h + 1;
xtable = Table[0, {i, 1, n}];
xtable[[1]] = x0;
Do[k1 = fp[xtable[[i - 1]], t0 + (i - 2) h];
k2 = fp[xtable[[i - 1]] + h/2*k1, t0 + (i - 1.5) h];
k3 = fp[xtable[[i - 1]] + h/2*k2, t0 + (i - 1.5) h];
k4 = fp[xtable[[i - 1]] + h*k3, t0 + (i - 1) h];
xtable[[i]] = xtable[[i - 1]] + h (k1 + 2 k2 + 2 k3 + k4)/6, {i, 2,
n}];
Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
Data2)
Clear[x, xtable]
a = DSolve[{x'[t] == t*x[t]^2 + 2*x[t], x[0] == -5}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := t*x^2 + 2*x;
Data2 = RK4Method[fp, -5.0, 0.3, 0, 5];
Plot[x, {t, 0, 5}, Epilog -> {PointSize[Large], Point[Data2]}, AxesOrigin -> {0, 0}, AxesLabel -> {"t", "x"}, PlotRange -> All]
Title = {"t_i", "x_i"};
Data2 = Prepend[Data2, Title];
Data2 // MatrixForm
View Python Code
# UPGRADE: need Sympy 1.2 or later, upgrade by running: "!pip install sympy --upgrade" in a code cell
# !pip install sympy --upgrade
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
sp.init_printing(use_latex=True)
def RK4Method(fp, x0, h, t0, tmax):
n = int((tmax - t0)/h + 1)
xtable = [0 for i in range(n)]
xtable[0] = x0
for i in range(1,n):
k1 = fp(xtable[i - 1], t0 + (i - 1)*h)
k2 = fp(xtable[i - 1] + h/2*k1, t0 + (i - 0.5)*h)
k3 = fp(xtable[i - 1] + h/2*k2, t0 + (i - 0.5)*h)
k4 = fp(xtable[i - 1] + h*k3, t0 + i*h)
xtable[i] = xtable[i - 1] + h*(k1 + 2*k2 + 2*k3 + k4)/6
Data = [[t0 + i*h, xtable[i]] for i in range(n)]
return Data
x = sp.Function('x')
t = sp.symbols('t')
sol = sp.dsolve(x(t).diff(t) - t*x(t)**2 - 2*x(t), ics={x(0): -5})
display(sol)
def fp(x, t): return t*x**2 + 2*x
Data = RK4Method(fp, -5.0, 0.3, 0, 5)
x_val = np.arange(0,5,0.01)
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.scatter([point[0] for point in Data],[point[1] for point in Data],c='k')
plt.xlabel("t"); plt.ylabel("x")
plt.grid(); plt.show()
print(["t_i", "x_i"],"\n",np.vstack(Data))
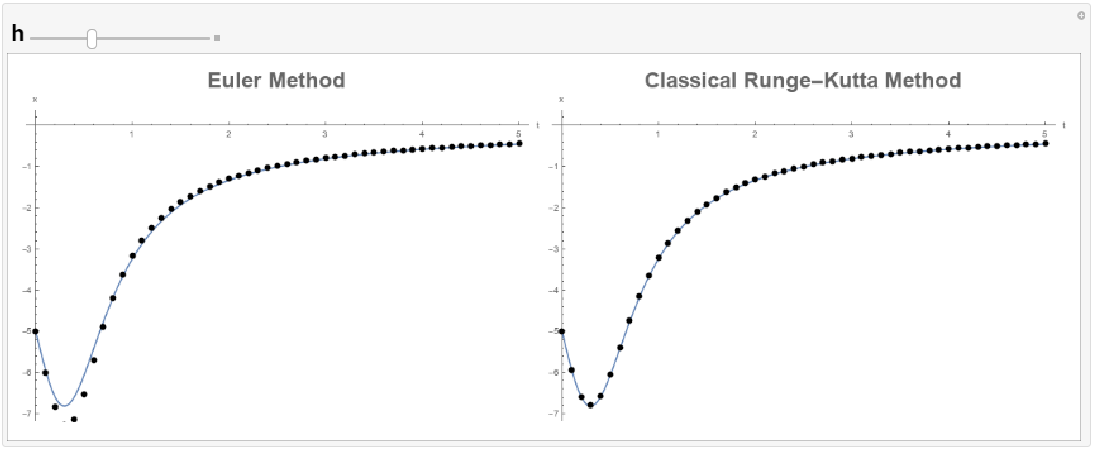
The following tool provides a comparison between the explicit Euler method and the classical Runge-Kutta method. The classical Runge-Kutta method gives excellent predictions even when ![]() , at which point the explicit Euler method fails to predict anything close to the exact equation. The classical Runge-Kutta method also provides better estimates than the midpoint method and Heun’s method above.
, at which point the explicit Euler method fails to predict anything close to the exact equation. The classical Runge-Kutta method also provides better estimates than the midpoint method and Heun’s method above.
Lecture Video