Engineering at Alberta Courses » The Midpoint Method

Solution Methods for IVPs: The Midpoint Method

The Midpoint Method

Similar to Heun’s method, the midpoint method provides a slight modification to both the implicit and explicit Euler methods. Consider the following IVP:

$\frac{\mathrm{d}x}{\mathrm{d}t}=F(x,t)$

Assuming that the value of the dependent variable $x$ (say $x_i$ ) is known at an initial value $t_i$ , then, we have:

$\int_{x_i}^{x_{i+1}}\!\frac{\mathrm{d}x}{\mathrm{d}t}\,\mathrm{d}t=\int_{t_i}^{t_{i+1}}\!F(x,t)\,\mathrm{d}t$

Therefore:

$x_{i+1}-x_i=\int_{t_i}^{t_{i+1}}\!F(x,t)\,\mathrm{d}t$

If the midpoint rule of the rectangle method of numerical integration is used for the right-hand side with one interval we obtain:

$x_{i+1}-x_i=hF\left(\frac{x_{i+1}+x_i}{2},\frac{t_{i+1}+t_{i}}{2}\right)+\mathcal{O}(h^3)$

where the error term is inherited from the use of $I_2$ in the rectangle rule. Therefore an estimate for $x_{i+1}$ is given by:

$x_{i+1}=x_i+hF\left(\frac{x_{i+1}+x_i}{2},\frac{t_{i+1}+t_{i}}{2}\right)+\mathcal{O}(h^3)$

Using this estimate, the local truncation error is thus proportional to the cube of the step size. If the errors from each interval are added together, with $n=\frac{L}{h}$ being the number of intervals and $L$ the total length $t_n-t_0$ , then, the total error is:

$E=\mathcal{O}(h^3) \frac{L}{h}=\mathcal{O}(h^2)$

which is similar to Heun’s method but better than both the implicit and explicit Euler methods. Note that the midpoint method is essentially a slight modification to the Euler’s method in which the slope used to calculate the value of $x_{i+1}$ at the next time point is used as the slope at the average point $x_{i+1/2}=\frac{x_{i+1}+x_i}{2}$ . The midpoint method can be implemented in two ways. One way is to use the slope at $x_i$ to calculate an initial estimate $x_{i+1/2}^{(0)}$ . Then, the estimate for $x_{i+1}$ would be calculated based on the slope at $x_{i+1/2}^{(0)}$ . Alternatively, the Newton-Raphson method or the fixed-point iteration method can be used to solve directly for $x_{i+1}$ . We will only adopt the first way. The following Mathematica code presents a procedure to utilize the midpoint method. The procedure is essentially similar to the ones presented in the Euler methods except for the step to calculate the new estimate $x_{i+1}$ .

View Mathematica Code

MidPointMethod[fp_, x0_, h_, t0_, tmax_] := 
(n = (tmax - t0)/h + 1;
  xtable = Table[0, {i, 1, n}];
  xtable[[1]] = x0;
  Do[xi120 = xtable[[i - 1]] + h/2*fp[xtable[[i - 1]], t0 + (i - 2) h]; 
   xtable[[i]] = xtable[[i - 1]] + h (fp[xi120, t0 + (i - 1-1/2) h]), {i, 2, n}];
  Data = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
  Data)

View Python Code

def MidPointMethod(fp, x0, h, t0, tmax):
  n = int((tmax - t0)/h + 1)
  xtable = [0 for i in range(n)]
  xtable[0] = x0
  for i in range(1,n):
    xi120 = xtable[i - 1] + h/2*fp(xtable[i - 1], t0 + (i - 1)*h)
    xtable[i] =  xtable[i - 1] + h*(fp(xi120, t0 + (i - 1/2)*h))
  Data = [[t0 + i*h, xtable[i]] for i in range(n)]
  return Data

Example

Solve Example 4 above using the midpoint method.

Solution

The midpoint method is implemented by first assuming an estimate for $x_{i+1/2}^{(0)}$ based on the explicit Euler method:

$x_{i+1/2}^{(0)}=x_i+\frac{h}{2}\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{x=x_{i},t=t_{i}}$

Then, the estimate for $x_{i+1}$ is calculated as:

$x_{i+1}=x_i+h\frac{\mathrm{d}x}{\mathrm{d}t}\bigg|_{x=x_{i+1/2}^{(0)},t=t_{i+1/2}}$

Setting $x_0=-5$ , $t_0=0$ , $t_1=0.1$ , and $h=0.1$ , an initial estimate for $x_{0.5}^{(0)}$ is given by:

$x_{0.5}^{(0)}=-5+\frac{h}{2}(t_0x_0^2+2x_0)=-5+\frac{0.1}{2}(0-10)=-5.5$

Using this information, the slope at $x_{0.5}^{(0)}$ can be calculated and used to estimate $x_1$ :

$x_1=-5+h\left(t_{0.5}\left(x_{0.5}^{(0)}\right)^2+2x_{0.5}^{(0)} \right)=-5.949$

Similarly, an initial estimate for $x_{1.5}^{(0)}$ is given by:

$x_{1.5}^{(0)}=-5.949+\frac{h}{2}(t_1x_1^2+2x_1)=-5.949+0.05(0.1(-5.949)^2-2\times 5.949)=-6.3667$

Using this information, the slope at $x_{1.5}^{(0)}$ can be calculated and used to estimate $x_2$ :

$x_2=-5.949+h\left(t_{1.5}\left(x_{1.5}^{(0)}\right)^2+2x_{1.5}^{(0)}\right)=-6.614$

Proceeding iteratively gives the values of $x_i$ up to $t=5$ . The Microsoft Excel file MidPoint.xlsx provides the required calculations.

The following graph shows the produced numerical data (black dots) overlapping the exact solution (blue line). The Mathematica code is given below.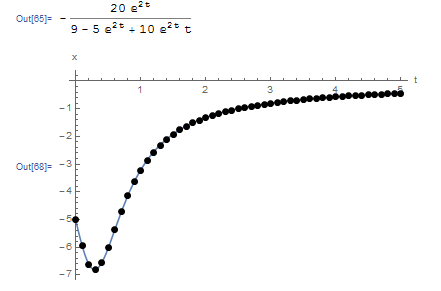

View Mathematica Code

MidPointMethod[fp_, x0_, h_, t0_, tmax_] := (n = (tmax - t0)/h + 1;
  xtable = Table[0, {i, 1, n}];
  xtable[[1]] = x0;
  Do[xi120 = xtable[[i - 1]] + h/2*fp[xtable[[i - 1]], t0 + (i - 2) h];
   xtable[[i]] =  xtable[[i - 1]] + h (fp[xi120, t0 + (i - 1 - 1/2) h]), {i, 2, n}];
  Data2 = Table[{t0 + (i - 1)*h, xtable[[i]]}, {i, 1, n}];
  Data2)
Clear[x, xtable]
a = DSolve[{x'[t] == t*x[t]^2 + 2*x[t], x[0] == -5}, x, t];
x = x[t] /. a[[1]]
fp[x_, t_] := t*x^2 + 2*x;
Data2 = MidPointMethod[fp, -5.0, 0.1, 0, 5];
Plot[x, {t, 0, 5}, Epilog -> {PointSize[Large], Point[Data2]}, AxesOrigin -> {0, 0}, AxesLabel -> {"t", "x"}, PlotRange -> All]
Title = {"t_i", "x_i"};
Data2 = Prepend[Data2, Title];
Data2 // MatrixForm

View Python Code

# UPGRADE: need Sympy 1.2 or later, upgrade by running: "!pip install sympy --upgrade" in a code cell
# !pip install sympy --upgrade
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
sp.init_printing(use_latex=True)

def MidPointMethod(fp, x0, h, t0, tmax):
  n = int((tmax - t0)/h + 1)
  xtable = [0 for i in range(n)]
  xtable[0] = x0
  for i in range(1,n):
    xi120 = xtable[i - 1] + h/2*fp(xtable[i - 1], t0 + (i - 1)*h)
    xtable[i] =  xtable[i - 1] + h*(fp(xi120, t0 + (i - 1/2)*h))
  Data = [[t0 + i*h, xtable[i]] for i in range(n)]
  return Data

x = sp.Function('x')
t = sp.symbols('t')
sol = sp.dsolve(x(t).diff(t) - t*x(t)**2 - 2*x(t), ics={x(0): -5})
display(sol)
def fp(x, t): return t*x**2 + 2*x
Data = MidPointMethod(fp, -5.0, 0.1, 0, 5)
x_val = np.arange(0,5,0.01)
plt.plot(x_val, [sol.subs(t, i).rhs for i in x_val])
plt.scatter([point[0] for point in Data],[point[1] for point in Data],c='k')
plt.xlabel("t"); plt.ylabel("x")
plt.grid(); plt.show()
print(["t_i", "x_i"],"\n",np.vstack(Data))

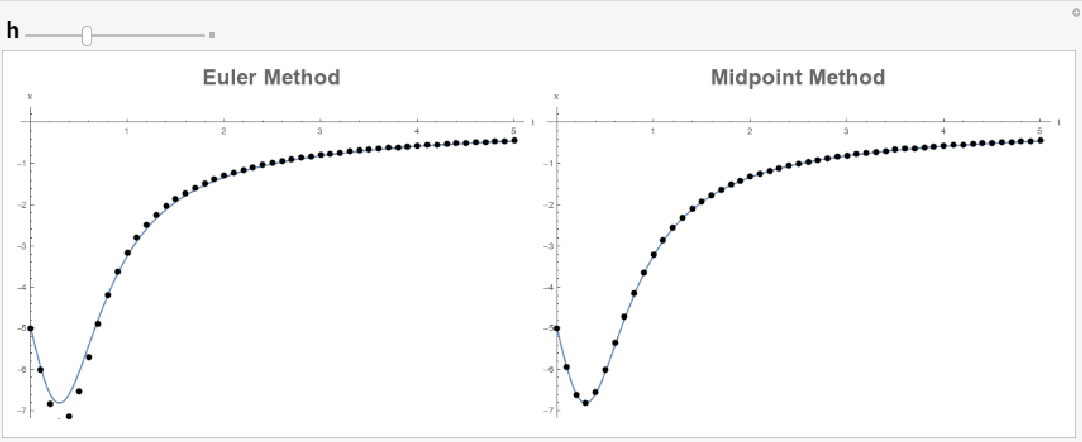
MATLAB files: File 1 (ex12_9.m) File 2 (midpoint.m)

The following tool provides a comparison between the explicit Euler method and the midpoint method. The midpoint method behaves very similar to Heun’s method. Notice that around $t\in[0,0.8]$ , the function $x$ varies highly in comparison to the rest of the domain. The biggest difference between midpoint method and the Euler method can be seen when $h=0.1$ around this area. The midpoint method is able to trace the curve while the Euler method has higher deviations.