Taylor Series: Mathematical Background
Definitions
Let ![]() be a smooth (differentiable) function, and let
be a smooth (differentiable) function, and let ![]() , then a Taylor series of the function
, then a Taylor series of the function ![]() around the point
around the point ![]() is given by:
is given by:
![]()
In particular, if ![]() , then the expansion is known as the Maclaurin series and thus is given by:
, then the expansion is known as the Maclaurin series and thus is given by:
![]()
Taylor’s Theorem
Many of the numerical analysis methods rely on Taylor’s theorem. In this section, a few mathematical facts are presented which serve as the basis for Taylor’s theorem. The ideas within the proofs presented here are attributed to Paul’s online calculus notes.
Extreme Values of Smooth Functions
Definition: Local Maximum and Local Minimum
Let ![]() .
. ![]() is said to have a local maximum at a point
is said to have a local maximum at a point ![]() if there exists an open interval
if there exists an open interval ![]() such that
such that ![]() and
and ![]() . On the other hand,
. On the other hand, ![]() is said to have a local minimum at a point
is said to have a local minimum at a point ![]() if there exists an open interval
if there exists an open interval ![]() such that
such that ![]() and
and ![]() . If
. If ![]() has either a local maximum or a local minimum at
has either a local maximum or a local minimum at ![]() , then
, then ![]() is said to have a local extremum at
is said to have a local extremum at ![]() .
.
Proposition 1
Let ![]() be smooth (differentiable). Assume that
be smooth (differentiable). Assume that ![]() has a local extremum (maximum or minimum) at a point
has a local extremum (maximum or minimum) at a point ![]() , then
, then ![]() . This proposition is also referred to in some texts as Fermat’s theorem.
. This proposition is also referred to in some texts as Fermat’s theorem.
View Proof of Proposition 1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This proposition simply means that if a smooth function attains a local maximum or minimum at a particular point, then the slope of the function is equal to zero at this point.
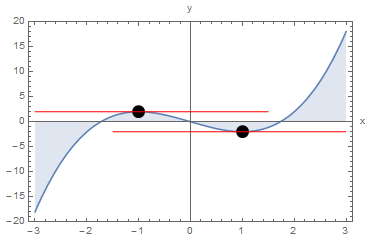
As an example, consider the function ![]() with the relationship
with the relationship ![]() . In this case,
. In this case, ![]() is a local maximum value for
is a local maximum value for ![]() attained at
attained at ![]() and
and ![]() is a local minimum value of
is a local minimum value of ![]() attained at
attained at ![]() . These local extrema values are associated with a zero slope for the function
. These local extrema values are associated with a zero slope for the function ![]() since
since
![]()
![]() and
and ![]() are locations of local extrema and for both we have
are locations of local extrema and for both we have ![]() . The red lines in the next figure show the slope of the function
. The red lines in the next figure show the slope of the function ![]() at the extremum values.
at the extremum values.
Clear[x]
y = x^3 - 3 x;
Plot[y, {x, -3, 3}, Epilog -> {PointSize[0.04], Point[{-1, 2}], Point[{1, -2}], Red, Line[{{-3, 2}, {1.5, 2}}], Line[{{3, -2}, {-1.5, -2}}]}, Filling -> Axis, PlotRange -> All, Frame -> True, AxesLabel -> {"x", "y"}]
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-3,3,0.01)
y = x**3 - 3*x
plt.plot(x,y)
plt.fill_between(x, y, 0, alpha=0.20)
plt.plot([-3,1.5],[2,2],'r')
plt.plot([3,-1.5],[-2,-2],'r')
plt.plot([-1,1],[2,-2],'ko')
plt.xlabel('x'); plt.ylabel('y')
plt.grid(); plt.show()
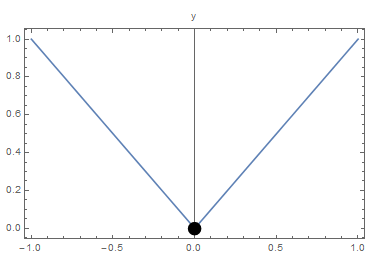
“Smoothness” or “Differentiability” is a very important requirement for the proposition to work. As an example, consider the function ![]() defined as
defined as ![]() . The function
. The function ![]() has a local minimum at
has a local minimum at ![]() , however,
, however, ![]() is not defined as the slope as
is not defined as the slope as ![]() from the right is different from the slope as
from the right is different from the slope as ![]() from the left as shown in the next figure.
from the left as shown in the next figure.
Clear[x]
y = Abs[x];
Plot[y, {x, -1, 1}, Epilog -> {PointSize[0.04], Point[{0, 0}]}, PlotRange -> All, Frame -> True, AxesLabel -> {"x", "y"}]
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-1,1,0.01)
y = abs(x)
plt.plot(x,y)
plt.plot([0],[0],'ko')
plt.xlabel('x'); plt.ylabel('y')
plt.grid(); plt.show()
Extreme Value Theorem
Statement: Let ![]() be continuous. Then,
be continuous. Then, ![]() attains its maximum and its minimum value at some points
attains its maximum and its minimum value at some points ![]() and
and ![]() in the interval
in the interval ![]() .
.
The theorem simply states that if we have a continuous function on a closed interval ![]() , then the image of
, then the image of ![]() contains a maximum value and a minimum value within the interval
contains a maximum value and a minimum value within the interval ![]() . The theorem is very intuitive. However, the proof is highly technical and relies on fundamental concepts in Real analysis including the definitions of real numbers and on continuous functions. You can review the Wikipedia entry or a course on Real analysis such as this one for details of the proof. For now, we will just illustrate the meaning of the theorem using an example. Consider the function
. The theorem is very intuitive. However, the proof is highly technical and relies on fundamental concepts in Real analysis including the definitions of real numbers and on continuous functions. You can review the Wikipedia entry or a course on Real analysis such as this one for details of the proof. For now, we will just illustrate the meaning of the theorem using an example. Consider the function ![]() defined as:
defined as:
![]()
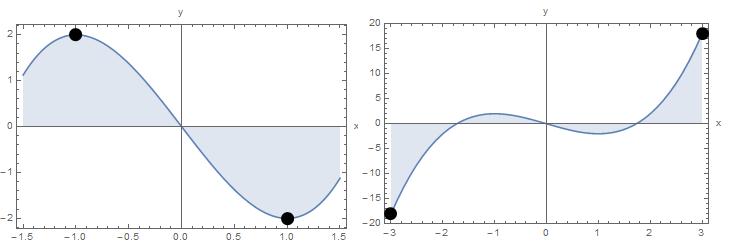
The theorem states that ![]() has to attain a maximum value and a minimum value at a point within the interval. In this case,
has to attain a maximum value and a minimum value at a point within the interval. In this case, ![]() is the maximum value of
is the maximum value of ![]() attained at
attained at ![]() and
and ![]() is the minimum value of
is the minimum value of ![]() attained at
attained at ![]() . Alternatively, if
. Alternatively, if ![]() with the same relationship as above,
with the same relationship as above, ![]() is the minimum value of
is the minimum value of ![]() attained at
attained at ![]() and
and ![]() is the maximum value of
is the maximum value of ![]() attained at
attained at ![]()
The following figure shows the graph of the function on the specified intervals.
Clear[x]
y = x^3 - 3 x;
Plot[y, {x, -1.5, 1.5}, Epilog -> {PointSize[0.04], Point[{-1, 2}], Point[{1, -2}]}, Filling -> Axis, PlotRange -> All, Frame -> True, AxesLabel -> {"x", "y"}]
Plot[y, {x, -3, 3}, Epilog -> {PointSize[0.04], Point[{-3, y /. x -> -3}], Point[{3, y /. x -> 3}]}, Filling -> Axis, PlotRange -> All, Frame -> True, AxesLabel -> {"x", "y"}]
import numpy as np
import matplotlib.pyplot as plt
x1 = np.arange(-1.5,1.5,0.01)
y1 = x1**3 - 3*x1
plt.plot(x1,y1)
plt.fill_between(x1, y1, 0, alpha=0.20)
plt.plot([-1,1],[2,-2],'ko')
plt.xlabel('x'); plt.ylabel('y')
plt.grid(); plt.show()
x2 = np.arange(-3,3,0.01)
def f(x): return x**3 - 3*x
y2 = f(x2)
plt.plot(x2,y2)
plt.fill_between(x2, y2, 0, alpha=0.20)
plt.plot([-3,3],[f(-3),f(3)],'ko')
plt.xlabel('x'); plt.ylabel('y')
plt.grid(); plt.show()
The condition that the function is defined on a closed interval ![]() is a crucial requirement for the extreme value theorem to hold true. Here is a counter example if this condition is relaxed. Let
is a crucial requirement for the extreme value theorem to hold true. Here is a counter example if this condition is relaxed. Let ![]() defined on the open interval
defined on the open interval ![]() . The function is unbounded; it keeps increasing as
. The function is unbounded; it keeps increasing as ![]() approaches
approaches ![]() . The figure below provides the plot of the function
. The figure below provides the plot of the function ![]() defined on the open interval
defined on the open interval ![]() . The function precipituously increases as it approaches the value of
. The function precipituously increases as it approaches the value of ![]() .
.

Rolle’s Theorem
Statement: Let ![]() be differentiable. Assume that
be differentiable. Assume that ![]() , then there is at least one point
, then there is at least one point ![]() where
where ![]() .
.
View Proof of Rolle's Theorem
![]()
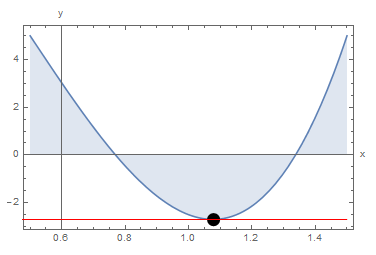
The Extreme Value Theorem ensures that there is a local maximum or local minimum within the interval, while proposition 1 ensures that at this local extremum, the slope of the function is equal to zero. As an example, consider the function ![]() defined as
defined as ![]() .
. ![]() . This ensures that there is a point
. This ensures that there is a point ![]() with
with ![]() . Indeed,
. Indeed, ![]() and the point
and the point ![]() is the location of the local minimum. The following figure shows the graph of the function on the specified interval along with the point
is the location of the local minimum. The following figure shows the graph of the function on the specified interval along with the point ![]() .
.
Clear[x]
y = 20 (x - 1/2)^3 - 20 (x - 1/2) + 5;
Expand[y]
y /. x -> 1.5
y /. x -> 0.5
y /. x -> (1/2 + 1/Sqrt[3])
D[y, x] /. x -> (1/2 + 1/Sqrt[3])
Plot[y, {x, 0.5, 1.5}, Epilog -> {PointSize[0.04], Point[{1/2 + 1/Sqrt[3], y /. x -> 1/2 + 1/Sqrt[3]}], Red, Line[{{-3, y /. x -> 1/2 + 1/Sqrt[3]}, {1.5, y /. x -> 1/2 + 1/Sqrt[3]}}]}, Filling -> Axis, PlotRange -> All, Frame -> True, AxesLabel -> {"x", "y"}]
import math
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
def f(x): return 20*(x - 1/2)**3 - 20*(x - 1/2) + 5
print("y(1.5):",f(1.5))
print("y(0.5):",f(0.5))
print("y(1/2 + 1/math.sqrt(3)):",f(1/2 + 1/math.sqrt(3)))
x1 = sp.symbols('x')
print("dy/dx(1/2 + 1/math.sqrt(3)):",sp.diff(20*(x1 - 1/2)**3 - 20*(x1 - 1/2) + 5,x1).subs(x1,1/2 + 1/math.sqrt(3)))
x = np.arange(0.5,1.5,0.01)
y = 20*(x - 1/2)**3 - 20*(x - 1/2) + 5
plt.plot(x,y)
plt.fill_between(x, y, 0, alpha=0.20)
plt.plot([1/2 + 1/math.sqrt(3)],[f(1/2 + 1/math.sqrt(3))],'ko')
plt.plot([0.5,1.5],[f(1/2 + 1/math.sqrt(3)),f(1/2 + 1/math.sqrt(3))],'r')
plt.xlabel('x'); plt.ylabel('y')
plt.grid(); plt.show()
Generalized Rolle’s Thoerem
Statement: Let ![]() be
be ![]() times differentiable. Assume that
times differentiable. Assume that ![]() is equal to zero at
is equal to zero at ![]() distinct points
distinct points ![]() , then there is at least one point
, then there is at least one point ![]() where
where ![]() .
.
View Proof of the Generalized Rolle's Theorem
![]()
![]()
Mean Value Theorem
Statement: Let ![]() be differentiable. Then, there is at least one point
be differentiable. Then, there is at least one point ![]() such that
such that ![]() .
.
View Proof of Mean Value Theorem
![]()
![]()
![]()
The mean value theorem states that there is a point ![]() inside the interval such that the slope of the function at
inside the interval such that the slope of the function at ![]() is equal to the average slope along the interval. The following example will serve to illustrate the main concept of the mean value theorem. Consider the function
is equal to the average slope along the interval. The following example will serve to illustrate the main concept of the mean value theorem. Consider the function ![]() defined as:
defined as:
![]()
The slope or first derivative of
![]()
The average slope of
![]()
The two points
![]()
The figure below shows the function ![]() on the specified interval. The line representing the average slope is shown in black connecting the points
on the specified interval. The line representing the average slope is shown in black connecting the points ![]() and
and ![]() . The red lines show the slopes at the points
. The red lines show the slopes at the points ![]() and
and ![]() .
.

Clear[x]
y = x^3 - 3 x;
averageslope = ((y /. x -> 3) - (y /. x -> -3))/(3 + 3)
dydx = D[y, x];
a = Solve[D[y, x] == averageslope, x]
Point1 = {x /. a[[1, 1]], y /. a[[1, 1]]}
Point2 = {x /. a[[2, 1]], y /. a[[2, 1]]}
Plot[y, {x, -3, 3}, Epilog -> {PointSize[0.04], Point[{-3, y /. x -> -3}], Point[{3, y /. x -> 3}], Line[{{-3, y /. x -> -3}, {3, y /. x -> 3}}], Point[Point1],Point[Point2], Red, Line[{Point1 + {-1, -averageslope}, Point1, Point1 + {1, averageslope}}], Line[{Point2 + {-1, -averageslope}, Point2, Point2 + {1, averageslope}}]}, Filling -> Axis, PlotRange -> All, Frame -> True, AxesLabel -> {"x", "y"}]
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
def f(x): return x**3 - 3*x
averageSlope = (f(3) - f(-3))/(3 + 3)
print("averageSlope:",averageSlope)
x1 = sp.symbols('x')
dydx = sp.diff(x1**3 - 3*x1,x1)
print("dy/dx:",dydx)
sol = list(sp.solveset(dydx - averageSlope,x1))
print("Solve:",sol)
Point1 = [sol[0], f(sol[0])]
Point2 = [sol[1], f(sol[1])]
print("Point1:",Point1)
print("Point2:",Point2)
x = np.arange(-3,3,0.01)
y = x**3 - 3*x
plt.plot(x,y)
plt.fill_between(x, y, 0, alpha=0.20)
plt.plot([-3,3,Point1[0],Point2[0]],[f(-3),f(3),Point1[1],Point2[1]],'ko')
plt.plot([Point1[0]-1,Point1[0]+1,Point1[0]],
[Point1[1]-averageSlope,Point1[1]+averageSlope,Point1[1]],'r')
plt.plot([Point2[0]-1,Point2[0]+1,Point2[0]],
[Point2[1]-averageSlope,Point2[1]+averageSlope,Point2[1]],'r')
plt.plot([-3,3],[f(-3),f(3)],'k')
plt.xlabel('x'); plt.ylabel('y')
plt.grid(); plt.show()
First and Second Derviative Tests
The Mean Value Theorem precipitates two important results that are fundamental to analyze the behaviour of functions around their extreme values. First, we define the notion of increasing and decreasing functions
Definition: Increasing and Decreasing Functions
Let ![]() , then:
, then:
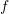 is increasing if
is increasing if 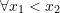 in
in 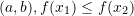
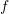 is decreasing if
is decreasing if 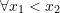 in
in 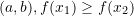
A function is stricly increasing or decreasing if ![]() or
or ![]() respectively.
respectively.
Proposition 2: First Derivative Test
Let ![]() be a continuous and smooth function. Then:
be a continuous and smooth function. Then:
- If
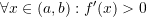 then
then 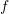 is increasing
is increasing - If
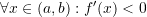 then
then 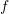 is decreasing
is decreasing - If
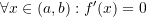 then
then 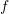 is constant
is constant
View Proof of the First Derivative Test
![]()
![]()
Proposition 3: Second Derivative Test
Let ![]() be a continuous and smooth function. Let
be a continuous and smooth function. Let ![]() be such that
be such that ![]() . Then:
. Then:
- If
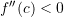 then
then  is a local maximum
is a local maximum - If
 then
then  is a local minimum
is a local minimum
View Proof of the Second Derivative Test
![]()
![]()
![]()
This proposition is very important for optimization problems when a local maximum or minimum is to be obtained for a particular function. In order to identify whether the solution corresponds to a local maximum or minimum, the second derivative of the function can be evaluated. Considering the example given above under Proposition 1, the second derivative is given by:
![]()
We have already identified ![]() and
and ![]() as locations of the local extremum values. To know whether they are local maxima or local minima, we can evaluate the second derivative at these points.
as locations of the local extremum values. To know whether they are local maxima or local minima, we can evaluate the second derivative at these points. ![]() . Therefore,
. Therefore, ![]() is the location of a local minimum, while
is the location of a local minimum, while ![]() implying that
implying that ![]() is the location of a local maximum.
is the location of a local maximum.
Taylor’s Theorem
As an introduction to Taylor’s Theorem, let’s assume that we have a function ![]() that can be represented as a polynomial function in the following form:
that can be represented as a polynomial function in the following form:
![]()
where ![]() is a fixed point and
is a fixed point and ![]() is a constant. The best way to find these constants is to find
is a constant. The best way to find these constants is to find ![]() and its derivatives when
and its derivatives when ![]() . So, when
. So, when ![]() we have:
we have:
![]()
Therefore, ![]() .
.
The derivatives of ![]() have the form:
have the form:
![Rendered by QuickLaTeX.com \[\begin{split}f'(x)&=b_1 +2b_2(x-a)+3b_3(x-a)^2+4b_4(x-a)^3+\cdots + nb_n(x-a)^{(n-1)}+\cdots\\f''(x)&=2b_2+2\times 3b_3(x-a)+3\times 4b_4(x-a)^2+\cdots + (n-1)nb_n(x-a)^{(n-2)}+\cdots\\\cdots\\f^{(n)}(x)&=n!b_n+\cdots\\\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-55585046a6841cc49d42f28305db9f68_l3.png)
The derivatives of ![]() when
when ![]() have the form:
have the form:
![Rendered by QuickLaTeX.com \[\begin{split}f'(a)&=b_1 +2b_2(a-a)+3b_3(a-a)^2+4b_4(a-a)^3+\cdots + nb_n(a-a)^{(n-1)}+\cdots\\f''(a)&=2b_2+2\times 3b_3(a-a)+3\times 4b_4(a-a)^2+\cdots + (n-1)nb_n(a-a)^{(n-2)}+\cdots\\\cdots\\f^{(n)}(a)&=n!b_n+\cdots\end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f5880c598acded36dd477a273229ecca_l3.png)
Therefore,
![]()
The above does not really serve as a rigorous proof for Taylor’s Theorem but rather an illustration that if an infinitely differentiable function can be represented as the sum of an infinite number of polynomial terms, then, the Taylor series form of a function defined at the beginning of this section is obtained. The following is the exact statement of Taylor’s Theorem:
Statement of Taylor’s Theorem: Let ![]() be
be ![]() times differentiable on an open interval
times differentiable on an open interval ![]() . Let
. Let ![]() . Then,
. Then, ![]() between
between ![]() and
and ![]() such that:
such that:
![]()
There are many proofs that can be found online for Taylor’s Theorem. Fundamentally, all of them rely on the Mean Value Theorem. We provide one proof in the expandable box below.
View Proof of Taylor's Theorem
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\begin{split} H'(t)&=G'(t)+(n+1)\left(\frac{(x-t)^n}{(x-a)^{n+1}}\right)G(a)\\ &=-\frac{f^{(n+1)}(t)}{n!}(x-t)^n+(n+1)\left(\frac{(x-t)^n}{(x-a)^{n+1}}\right)G(a) \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0193be5e3c66d8861c1d60062dc117ce_l3.png)
![]()
![]()
![]()
![]()
Explanation and Importance: Taylor’s Theorem has numerous implications in analysis in engineering. In the following we will discuss the meaning of the theorem and some of its implications:
-
Simply put, Taylor’s Theorem states the following: if the function
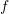 and its
and its 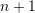 derivatives are known at a point
derivatives are known at a point  , then, the function at a point
, then, the function at a point  away from
away from  can be approximated by the value of the Taylor’s approximation
can be approximated by the value of the Taylor’s approximation 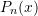 :
:![Rendered by QuickLaTeX.com \[f(x)\approx P_n(x)=f(a)+f'(a) (x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-280fbd3bb373138a94f3d2aa60117b0c_l3.png)
The error (difference between the approximation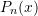 and the exact
and the exact 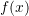 is given by:
is given by:
![Rendered by QuickLaTeX.com \[E=f(x)-P_n(x)=\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-a)^{n+1}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-00aa24ce878ea01844b97fb7824b62a9_l3.png)
The term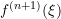 is bounded since
is bounded since 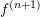 is a continuous function on the interval from
is a continuous function on the interval from  to
to  . Therefore, when
. Therefore, when 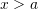 , the upper bound of the error can be given as:
, the upper bound of the error can be given as:
![Rendered by QuickLaTeX.com \[|E|\leq \max_{\xi\in[a,x]}\frac{|f^{(n+1)}(\xi)|}{(n+1)!}(x-a)^{n+1}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e677cce3900e2a9cd403c32c21628288_l3.png)
While, when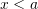 , the upper bound of the error can be given as:
, the upper bound of the error can be given as:
![Rendered by QuickLaTeX.com \[|E|\leq \max_{\xi\in[x,a]}\frac{|f^{(n+1)}(\xi)|}{(n+1)!}(a-x)^{n+1}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-73437ae1a6ccccf30ce7f19ee7b1e078_l3.png)
The above implies that the error is directly proportional to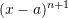 . This is traditionally written as follows:
. This is traditionally written as follows:![Rendered by QuickLaTeX.com \[f(x)=P_n(x)+\mathcal{O} (h^{n+1})\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-847e0157b763e3956bd2b7ee43a0fefd_l3.png)
where
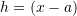 . In other words, as
. In other words, as  gets smaller and smaller, the error gets smaller in proportion to
gets smaller and smaller, the error gets smaller in proportion to 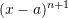 . As an example, if we choose
. As an example, if we choose 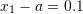 and then
and then 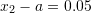 , then,
, then, 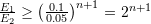 . I.e., if the step size is halved, the error is divided by
. I.e., if the step size is halved, the error is divided by  .
. -
If the function
![Rendered by QuickLaTeX.com f:[c,d]\rightarrow \mathbb{R}](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8fcfc289aafe81978155b67b9cedfca2_l3.png) is infinitely differentiable on an interval
is infinitely differentiable on an interval 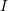 , and if
, and if  , then
, then 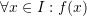 is the limit of the sum of the Taylor series. The error which is the difference between the infinite sum and the approximation is called the truncation error as defined in the error section.
is the limit of the sum of the Taylor series. The error which is the difference between the infinite sum and the approximation is called the truncation error as defined in the error section. -
There are many rigorous proofs available for Taylor’s Theorem and the majority rely on the mean value theorem above. Notice that if we choose
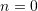 , then the mean value theorem is obtained. For a rigorous proof, you can check one of these links: link 1 or link 2. Note that these proofs rely on the mean value theorem. In particular, L’Hôpital’s rule was used in the Wikipedia proof which in turn relies on the mean value theorem.
, then the mean value theorem is obtained. For a rigorous proof, you can check one of these links: link 1 or link 2. Note that these proofs rely on the mean value theorem. In particular, L’Hôpital’s rule was used in the Wikipedia proof which in turn relies on the mean value theorem.
The following code illustrates the difference between the function ![]() and the Taylor’s polynomial
and the Taylor’s polynomial ![]() . You can download the code, change the function, the point
. You can download the code, change the function, the point ![]() , and the range of the plot to see how the Taylor series of other functions behave.
, and the range of the plot to see how the Taylor series of other functions behave.
Taylor[y_, x_, a_, n_] := (y /. x -> a) +
Sum[(D[y, {x, i}] /. x -> a)/i!*(x - a)^i, {i, 1, n}]
f = Sin[x] + 0.01 x^2;
Manipulate[
s = Taylor[f, x, 1, nn];
Grid[{{Plot[{f, s}, {x, -10, 10}, PlotLabel -> "f(x)=Sin[x]+0.01x^2",
PlotLegends -> {"f(x)", "P(x)"},
PlotRange -> {{-10, 10}, {-6, 30}},
ImageSize -> Medium]}, {Expand[s]}}], {nn, 1, 30, 1}]
import math
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from ipywidgets.widgets import interact
def taylor(f,xi,a,n):
return sum([(f.diff(x1,i).subs(x1,a))/math.factorial(i)*(xi - a)**i for i in range(n)])
x1 = sp.symbols('x')
f = sp.sin(x1) + 0.01*x1**2
@interact(n=(1,30,1))
def update(n=1):
x = np.arange(-10,10,0.1)
y = np.sin(x) + 0.01*x**2
plt.plot(x,y, label="f(x)")
p = [taylor(f,xi,1,n) for xi in x]
plt.plot(x,p, label="P(x)")
plt.title(" ")
plt.xlabel('x'); plt.ylabel('y')
plt.ylim(-6,30); plt.xlim(-10,10)
plt.legend(); plt.grid(); plt.show()
print(sp.series(f,x1,0,n))
")
plt.xlabel('x'); plt.ylabel('y')
plt.ylim(-6,30); plt.xlim(-10,10)
plt.legend(); plt.grid(); plt.show()
print(sp.series(f,x1,0,n))
The following tool illustrates the difference between the function ![]() and the Taylor’s polynomial
and the Taylor’s polynomial ![]() . You can change the order of the series expansion to see how the Taylor series of the function behave.
. You can change the order of the series expansion to see how the Taylor series of the function behave.
The Mathematica function Series can also be used to generate the Taylor expansion of any function:
Series[Tan[x],{x,0,7}]
Series[1/(1+x^2),{x,0,10}]
import sympy as sp
sp.init_printing(use_latex=True)
x = sp.symbols('x')
display("tan(x):",sp.series(sp.tan(x),x,0,8))
display("1/(1+x**2):",sp.series(1/(1+x**2),x,0,11))
The following tool shows how the Taylor series expansion around the point ![]() , termed
, termed ![]() in the figure, can be used to provide an approximation of different orders to a cubic polynomial, termed
in the figure, can be used to provide an approximation of different orders to a cubic polynomial, termed ![]() in the figure. Use the buttons to change the order of the series expansion. The tool provides the error at
in the figure. Use the buttons to change the order of the series expansion. The tool provides the error at ![]() , namely
, namely ![]() . What happens when the order reaches 3?
. What happens when the order reaches 3?
Polynomial Interpolation Error
While not related to the Taylor’s Theorem, the error in the interpolating polynomial can be shown to have a form similar to the Taylor’s Theorem error term. The following theorem will be used later in the book when evaluating the error associated with the interpolating polynomial. Similar to Taylor’s Theorem, the proof relies on the Mean Value Theorem above.
Statement of Polynomial Interpolation Error Theorem: Let ![]() be
be ![]() times differentiable on an open interval
times differentiable on an open interval ![]() . Let
. Let ![]() and define the
and define the ![]() degree interpolating polynomial
degree interpolating polynomial
![]()
Then, ![]() between
between ![]() and
and ![]() such that:
such that:
![]()
View Proof of Polynomial Interpolation Error Theorem
![]()
![]()
![]()
![]()
![]()
![]()

This was expertly explained. I know this is a conceptual topic that requires focus and clear definition. I appreciated this resource a lot.
Thank you!