Open Educational Resources

Direct Methods: Cholesky Factorization for Positive Definite Symmetric Matrices

The Method

Positive definite symmetric matrices appear naturally in many engineering problems. In particular, the stiffness matrices of elastic structures that appear in the stiffness method and the finite element analysis method for structural engineering applications are positive definite symmetric matrices. Positive definite symmetric matrices, as shown in this section have positive eigenvalues and so working with them can be very easy. Also, being symmetric, only one half of the off diagonal components need to be stored which reduces the computational time significantly. The Cholesky Factorization is a particular type of LU decomposition that can be applied to symmetric matrices. In particular, a positive definite symmetric matrix can be decomposed such that:

    \[ A=LL^T=U^TU \]

Where L=U^T is a lower triangular matrix and its transpose L^T=U is an upper triangular matrix. For example, the following symmetric matrix is positive definite (because all its eigenvalues when calculated are positive):

    \[ A=\left(\begin{matrix}1&3&2\\3&13&8\\2&8&6\end{matrix}\right) \]

A admits the following decomposition A=U^TU:

    \[ \left(\begin{matrix}1&3&2\\3&13&8\\2&8&6\end{matrix}\right)=\left(\begin{matrix}1&0&0\\3&2&0\\2&1&1\end{matrix}\right)\left(\begin{matrix}1&3&2\\0&2&1\\0&0&1\end{matrix}\right) \]

This decomposition is similar to the LU decomposition and if a linear system Ax=b is such that A is positive definite, then the Cholesky decomposition enables the quick calculation of U and then the backward and forward substitution can be used to solve the system (as shown in the LU decomposition section). The factorization can be found by noticing that the diagonal entry of A admits the following:

    \[ A_{ii}=\sum_{k=1}^nU_{ki}U_{ki}=\sum_{k=1}^iU_{ki}U_{ki}=\sum_{k=1}^{i-1}U_{ki}U_{ki}+U_{ii}^2 \]

where the fact that U_{ki}=0 whenever k>i was used. Therefore:

(1)   \begin{equation*} U_{ii}=\sqrt{A_{ii}-\sum_{k=1}^{i-1}U_{ki}U_{ki}} \end{equation*}

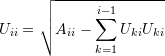
On the other hand, an off diagonal component A_{ij} admits the following:

    \[ A_{ij}=\sum_{k=1}^nU_{ki}U_{kj}=\sum_{k=1}^iU_{ki}U_{kj}=\sum_{k=1}^{i-1}U_{ki}U_{kj}+U_{ii}U_{ij} \]

where again, the fact that U_{ki}=0 whenever k>i was used. Therefore:

(2)   \begin{equation*} U_{ij}=\frac{A_{ij}-\sum_{k=1}^{i-1}U_{ki}U_{kj}}{U_{ii}} \end{equation*}

Notice that for the factorization to work, we can’t have negative values for A_{ii} or zero values for U_{ii} which is guaranteed not to occur because A is positive definite.

Programming the Method

Equations 1 and 2 can be programmed by first setting i=1, then iterating j from 2 to n. Then, setting i=2 and iterating j from 3 to n and so on. As an illustration, we will apply the algorithm for

    \[ A=\left(\begin{matrix}1&3&2\\3&13&8\\2&8&6\end{matrix}\right) \]

Setting i=1 in Equation 1 yields:

    \[ U_{11}=\sqrt{A_{11}}=\sqrt{1}=1 \]

Iterating j from 2 to 3 in Equation 2 yields:

    \[ U_{12}=\frac{A_{12}}{U_{11}}=3\qquad U_{13}=\frac{A_{13}}{U_{11}}=2 \]

Setting i=2 in Equation 1 yields:

    \[ U_{22}=\sqrt{A_{22}-U_{12}U_{12}}=\sqrt{13-9}=2 \]

Iterating j from 3 to 3 in Equation 2 yields:

    \[ U_{23}=\frac{A_{23}-U_{12}U_{13}}{U_{22}}=\frac{8-3\times 2}{2}=1 \]

Finally, setting i=3 in Equation 1 yields:

    \[ U_{33}=\sqrt{A_{33}-U_{13}U_{13}-U_{23}U_{23}}=\sqrt{6-4-1}=1 \]

Which yields the following matrix U:

    \[ U=\left(\begin{matrix}1&3&2\\0&2&1\\0&0&1\end{matrix}\right) \]

The following is the Mathematica code for the algorithm, along with the code to solve a linear system of equations Ax=b with A being positive definite. The algorithm is divided into two procedures. The first procedure calculates the Cholesky Decompsition of a matrix and the second procedure uses U and U^T for backward and forward substitution as described in the LU decomposition. It should be noted that in general the Cholesky Decomposition should be much more efficient than the LU decomposition for positive definite symmetric matrices. However, the code below will need to be optimized to achieve that.

View Mathematica Code
CD[A_] :=
 (n = Length[A];
  U = Table[0, {i, 1, n}, {j, 1, n}];
  Do[U[[i, i]] = Sqrt[A[[i, i]] - Sum[U[[k, i]] U[[k, i]], {k, 1, i - 1}]];U[[i, j]] = (A[[i, j]] - Sum[U[[k, i]] U[[k, j]], {k, 1, i - 1}])/U[[i, i]], {i, 1, n}, {j, i, n}];
  U)
CDAB[A_, b_] := 
(n = Length[A];
  U = CD[A];
  L = Transpose[U];
  y = Table[0, {i, 1, n}];
  x = Table[0, {i, 1, n}];
  For[i = 1, i <= n,i = i + 1, (BB = 0; Do[BB = L[[i, l]]*y[[l]] + BB, {l, 1, i - 1}]; y[[i]] = (b[[i]] - BB)/L[[i, i]])];
  For[i = n, i >= 1, i = i - 1, (BB = 0; Do[BB = U[[i, l]]*x[[l]] + BB, {l, i + 1, n}]; x[[i]] = (y[[i]] - BB)/U[[i, i]])];
  x)
A = {{39, 25, 36, 26}, {25, 21, 24, 18}, {36, 24, 34, 24}, {26, 18, 24, 33}};
b = {-196, 392, 0, 490}
N[CDAB[A, b]]
FullSimplify[CDAB[A, b]]
View Python Code
import numpy as np
def CD(A):
  A = np.array(A)
  n = len(A)
  U = np.zeros([n,n])
  for i in range(n):
    for j in range(i, n):
      U[i, i] = np.sqrt(A[i, i] - sum([U[k, i]*U[k, i] for k in range(i)]))
      U[i, j] = (A[i, j] - sum([U[k, i]*U[k, j] for k in range(i)]))/U[i, i]
  return U

def CDAB(A,b):
  n = len(A)
  U = CD(A)
  L = U.T
  y = np.zeros(n)
  x = np.zeros(n)
  for i in range(n):
    BB = 0
    for l in range(i):
      BB = L[i, l]*y[l] + BB
    y[i] = (b[i] - BB)/L[i, i]
  for i in range(n-1,-1,-1):
    BB = 0
    for l in range(i+1, n):
      BB = U[i, l]*x[l] + BB
    x[i] = (y[i] - BB)/U[i, i]
  return x

A = [[39, 25, 36, 26], [25, 21, 24, 18], [36, 24, 34, 24], [26, 18, 24, 33]]
b = [-196, 392, 0, 490]
CDAB(A, b)

The above code relies on using the “Sum” command in Mathematica which is not very efficient. The following code is more efficient and uses the “Do” command for the sum function:

View Mathematica Code
CD[A_] := 
  (n = Length[A];
  U = Table[0, {i, 1, n}, {j, 1, n}];
  Do[BB = 0; Do[BB = BB + U[[k, i]] U[[k, i]], {k, 1, i - 1}]; 
   U[[i, i]] = Sqrt[A[[i, i]] - BB]; 
   Do[BB = 0; Do[BB = BB + U[[k, i]] U[[k, j]], {k, 1, i - 1}]; 
    U[[i, j]] = (A[[i, j]] - BB)/U[[i, i]], {j, i + 1, n}], {i, 1, n}];
  U)
CDAB[A_, b_] := (n = Length[A];
  U = CD[A];
  L = Transpose[U];
  y = Table[0, {i, 1, n}];
  x = Table[0, {i, 1, n}];
  For[i = 1, i <= n, i = i + 1, (BB = 0; Do[BB = L[[i, l]]*y[[l]] + BB, {l, 1, i - 1}]; y[[i]] = (b[[i]] - BB)/L[[i, i]])];
  For[i = n, i >= 1,i = i - 1, (BB = 0; Do[BB = U[[i, l]]*x[[l]] + BB, {l, i + 1, n}]; x[[i]] = (y[[i]] - BB)/U[[i, i]])];
  x)
A = {{39, 25, 36, 26}, {25, 21, 24, 18}, {36, 24, 34, 24}, {26, 18, 24, 33}};
b = {-196, 392, 0, 490}
N[CDAB[A, b]]
FullSimplify[CDAB[A, b]]
View Python Code
import numpy as np
def CD(A):
  A = np.array(A)
  n = len(A)
  U = np.zeros([n,n])
  for i in range(n):
    BB = 0
    for k in range(i):
      BB = BB + U[k, i]*U[k, i]
    U[i, i] = np.sqrt(A[i, i] - BB) 
    for j in range(i,n):
      BB = 0
      for k in range(i):
        BB = BB + U[k, i]*U[k, j]
      U[i, j] = (A[i, j] - BB)/U[i, i]
  return U

def CDAB(A,b):
  n = len(A)
  U = CD(A)
  L = U.T
  y = np.zeros(n)
  x = np.zeros(n)
  for i in range(n):
    BB = 0
    for l in range(i):
      BB = L[i, l]*y[l] + BB
    y[i] = (b[i] - BB)/L[i, i]
  for i in range(n-1,-1,-1):
    BB = 0
    for l in range(i+1, n): 
      BB = U[i, l]*x[l] + BB 
    x[i] = (y[i] - BB)/U[i, i]
  return x
  
A = [[39, 25, 36, 26], [25, 21, 24, 18], [36, 24, 34, 24], [26, 18, 24, 33]]
b = [-196, 392, 0, 490]
CDAB(A, b)

Mathematica can be used to calculate the Cholesky Factorization using the function “CholeskyDecomposition[]” which outputs the matrix U in the decomposition A=U^TU.

View Mathematica Code
A={{1,3,2},{3,13,8},{2,8,6}}
U=CholeskyDecomposition[A]
Transpose[U].U//MatrixForm
View Python Code
import numpy as np
A = [[1,3,2], [3,13,8], [2,8,6]]
U = np.linalg.cholesky(A)
print(U.T)

We are providing two MATLAB files; the first calculates the decomposition, while the second solves a linear system of equation using the decomosition.

MATLAB file to calculate the Cholesky decompositionDownload
MATLAB file to solve a linear system using the Cholesky decompositionDownload

Leave a Reply

Your email address will not be published.