Engineering at Alberta Courses » Three-Dimensional Strain Measures

Strain Measures: Three-Dimensional Strain Measures

Learning Outcomes

Describe two different three-dimensional strain measures: The small strain and the Green strain tensors.
Small Strain Tensor: Compute the small strain tensor given a deformation function. Calculate the uniaxial engineering strain along various directions and the shear strain between perpendicular vectors, and the volumetric strain using the small strain tensor.
Compute the strain tensor components using the experimental results of a strain rosette.
Small Strain Tensor: Describe the implications of the symmetry of the small strain tensor: There is a coordinate system in which the off diagonal components are zero, i.e., no shear strains.Employ the process of diagonalization to find this coordinate system.
Small Strain Tensor: Explain the limitations of using the small strain tensor.Describe what the small strain tensor predicts under large rotations.
Green Strain Tensor: Compute the Green strain tensor given a deformation function.Calculate the Green uniaxial strain along various directions, using the Green strain tensor.
Green Strain Tensor: Describe the implications of its symmetry: There is a coordinate system in which the off diagonal components are zero, i.e., no shear strains. Employ the process of diagonalization to find this coordinate system.
Green Strain Tensor: Describe what the Green Strain Tensor predicts under large rotations.

Three Dimensional Strain Measures

In general, strain measures give a measure of how the lengths or angles change when we compare vectors in the undeformed configuration with vectors in the deformed configuration. If a tangent vector in the reference configuration is denoted $dX$ , while its deformed image is denoted $dx4$ , then we can calculate the various strain measures along the direction $dx$ by the simple computations:

$\varepsilon_{eng \hspace{1mm} along \hspace{1mm} dX} = \frac{\|dx\| - \|dX\|}{\|dX\|} \\ \varepsilon_{true \hspace{1mm} along \hspace{1mm} dX} = \ln\frac{\|dx\|}{\|dX\|} \\ \varepsilon_{Green \hspace{1mm} along \hspace{1mm} dX} = \frac{\|dx\|^2 - \|dX\|^2}{2\|dX\|^2}$

where we can use the relationship between the dot product and the norm when convenient:

$\|dx\|^2 = dx \cdot dx \hspace{5mm} \|dX\|^2 = dX \cdot dX$

However, a more convenient and traditional way to measure strain is to define strain tensors by which we can calculate strain along certain directions. We will discuss the two most common strain tensors in the literature:

Small (Infinitesimal) Strain Tensor

The small of infinitesimal strain tensor $\varepsilon$ is defined as the symmetric part of the displacement gradient $\nabla u$ :

$\varepsilon = \frac{\Delta u + \Delta u^T}{2}$

Which has the following component form:

$\varepsilon = \begin{pmatrix} \frac{\partial u_1}{\partial X_1} & \frac{1}{2}(\frac{\partial u_1}{\partial X_2} +\frac{\partial u_2}{\partial X_1}) & \frac{1}{2}(\frac{\partial u_1}{\partial X_3} + \frac{\partial u_3}{\partial X_1}) \\ \frac{1}{2}(\frac{\partial u_1}{\partial X_2} +\frac{\partial u_2}{\partial X_1}) & \frac{\partial u_2}{\partial X_2} & \frac{1}{2}(\frac{\partial u_2}{\partial X_3} + \frac{\partial u_3}{\partial X_2}) \\ \frac{1}{2}(\frac{\partial u_1}{\partial X_3} + \frac{\partial u_3}{\partial X_1}) & \frac{1}{2}(\frac{\partial u_2}{\partial X_3} + \frac{\partial u_3}{\partial X_2}) & \frac{\partial u_3}{\partial X_3} \\ \end{pmatrix}$

which can be written in a simple form as follows $\forall i,j\leq 3$ :

$\varepsilon_{ij} = \frac{1}{2}(\frac{\partial u_i}{\partial X_j} + \frac{\partial u_j}{\partial X_i})$

In the case of small deformations, the small strain tensor can be used to compute the engineering longitudinal and shear strains as shown below.

Calculating Longitudinal Strains Along General Vectors:

In the case of small deformations, the engineering longitudinal strain along a tangent vector $dX$ in the reference configuration can be calculated using the relationship:

$\varepsilon_{eng \hspace{1mm} along \hspace{1mm} dX} = \frac{dX \cdot \varepsilon dX}{\|dX\|^2}$

To show the above relationship, we are going to use the relationship between the deformed tangent vector $dx$ and its original vector $dX$ as shown in the displacement gradient tensor section:

$dx = dX + \varepsilon dX + W_{inf}dX$

The length of $dx$ can be estimated as follows:

$\|dx\| = \sqrt{dx \cdot dx} = \sqrt{(dX + \varepsilon dX + W_{fin} dX) \cdot (dX + \varepsilon dX + W_{inf} dX)}$

Since $W_{inf}$ is a skewsymmetric tensor, we have: $dX\cdot W_{inf}dX=0$ . For small deformations, the following terms can be neglected $W_{inf}dX\cdot W_{inf}dX$ , $\varepsilon dX\cdot W_{inf}dX$ and $\varepsilon dX\cdot \varepsilon dX$ which simplifies the above relationship to:

$\|dx\| \simeq \sqrt{dX \cdot dX + 2dX \cdot \varepsilon dX} \simeq \|dX\|\sqrt{1 + \frac{2dX \cdot \varepsilon dX}{dX \cdot dX}}$

Since the term $\frac{2dX\cdot\varepsilon dX}{dX\cdot dX} <<1$ , the above relationship can be further simplified as follows:

$\|dx\| \simeq \|dX\| + \frac{dX \cdot \varepsilon dX}{\|dX\|}$

Thus, for small deformations, the engineering strain along the reference configuration tangent vector $dX$ can be calculated as follows:

$\varepsilon_{eng \hspace{1mm} along \hspace{1mm} dX} = \frac{\|dx\| - \|dX\|}{\|dX\|} \simeq \frac{dX \cdot \varepsilon dX}{\|dX\|^2}$

Calculating Longitudinal Strains Along the Basis Vectors:

The strain along the basis vectors $e_1$ , $e_2$ and $e_3$ in the reference configuration can be calculated using the above relationship as follows $\forall i\leq 3$ :

$\varepsilon_{eng \hspace{1mm} along \hspace{1mm} e_i} \simeq \frac{e_i \cdot \varepsilon e_i}{\|e_i\|^2}$

Therefore,

$\varepsilon_{eng \hspace{1mm} along \hspace{1mm} e_1} \simeq \frac{\partial u_1}{\partial X_1} \hspace{5mm} \varepsilon_{eng \hspace{1mm} along \hspace{1mm} e_2} \simeq \frac{\partial u_2}{\partial X_2} \hspace{5mm} \varepsilon_{eng \hspace{1mm} along \hspace{1mm} e_3} \simeq \frac{\partial u_3}{\partial X_3}$

Therefore, the diagonal components of the strain matrix give the value of the longitudinal strains along the basis vectors of the reference configuration.

Calculating Angle Change Between General Vectors:

Given two vectors $dX$ and $dY$ separated by an angle $\Theta$ in the reference configuration that deform into the two vectors $dx$ and $dy$ separated by an angle $\theta$ in the deformed configuration, then half the change in the dot produce between the two vectors before and after deformation can be calculated as:

$\frac{1}{2} \frac{dx \cdot dy - dX \cdot dY}{\|dX\|\|dY\|} = \frac{1}{2}\frac{\|dx\|\|dy\|\cos\theta - \|dX\|\|dX\|\cos\Theta}{\|dX\|\|dY\|}$

Using the relationship between the deformed tangent vectors $dx$ , $dy$ and their original vectors $dX$ , $dY$ as shown in the displacement gradient tensor section we can write $dx$ and $dy$ as functions of $dX$ and $dY$ :

$dx \cdot dy = (dX + \varepsilon dX + W_{inf} dX) \cdot (dY + \varepsilon dY + W_{inf} dY)$

Since $\varepsilon$ is symmetric and $W_{inf}$ is skewsymmetric and for small deformations, the dot product can be approximated as follows:

$dx \cdot dy \simeq dX \cdot dY + 2dX \cdot \varepsilon dY$

Then half the change in the dot produce between the two vectors before and after deformation can be calculated using $\varepsilon$ as follows:

$\frac{1}{2} \frac{dx \cdot dy - dX \cdot dY}{\|dX\|\|dY\|} \simeq \frac{dX \cdot \varepsilon dY}{\|dX\|\|dY\|}$

When the deformations are small such that $\|dx\|\simeq\|dX\|$ and $\|dy\|\simeq\|dY\|$ then half the difference in the cosines of the angles before and after deformation can be calculated as follows:

$\frac{\cos\theta - \cos\Theta}{2} \simeq \frac{dX \cdot \varepsilon dY}{\|dX\|\|dY\|}$

If the original vectors $dX$ and $dY$ are orthogonal to each other, then $\cos\Theta=0$ . In that case, the above relationship gives half the engineering shear strain of planes parallel to $dX$ and perpendicular to $dY$ .

Calculating Engineering Shear Strain in the Planes of the Basis Vectors:

Using the above relationship, the engineering shear strains in the planes of the basis vectors $e_i$ and $e_j$ with $i\neq j$ can be calculated as follows:

$\gamma_{ij} = 2\frac{e_i \cdot \varepsilon e_j}{\|e_i\|\|e_j\|} = 2\varepsilon_{ij} = \frac{\partial u_i}{\partial X_j} + \frac{\partial u_j}{\partial X_i}$

i.e., the off diagonal components give the engineering shear strains in the planes $e_1$ – $e_2$ , $e_1$ – $e_3$ and $e_2$ – $e_3$

$\gamma_{12} = 2\varepsilon_{12} = \frac{\partial u_1}{\partial X_2} + \frac{\partial u_2}{\partial X_1} \hspace{5mm} \gamma_{13} = 2\varepsilon_{13} = \frac{\partial u_1}{\partial X_3} + \frac{\partial u_3}{\partial X_1} \hspace{5mm} \gamma_{23} = 2\varepsilon_{23} = \frac{\partial u_2}{\partial X_3} + \frac{\partial u_3}{\partial X_2} \hspace{5mm}$

EXAMPLE:

In the following example, a two dimensional square centred around the origin is deformed using the displacement relationship:

$x_1 = a_{11}X_{1} + a_{12}X_{2}$

$x_2 = a_{12}X_{2} + a_{22}X_{2}$

The following tool lets you vary the values of $a_{11}$ and $a_{22}$ between -0.8 and 1.2 and the values of $a_{12}$ and $a_{21}$ between -0.2 and 0.2. The tool then draws the square before deformation and then after deformation. You can also select two unit vectors $dX$ and $dY$ by varying their respective angles of inclination with the horizontal axis $\Theta_1$ and $\Theta_2$ . The two vectors are drawn before and after deformation. $dX$ is drawn in blue and $dY$ is drawn in red. The tool calculates the deformation gradient $F$ , the gradient of displacement tensor $\nabla u$ , the small strain matrix $\varepsilon$ and the infinitesimal rotation matrix $W_{inf}$ . The longitudinal strains along $dX$ and $dY$ are calculated underneath the figures in addition to $\cos\theta$ where $\theta$ is the angle between $dx$ and $dy$ which are the respective images of $dX$ and $dY$ . Vary the values of $a_{ij}$ to see their effect on the deformation and the components of the strain matrix $\varepsilon$ . Also, check your strain computations against the results shown for various choices of $dX$ and $dY$ . Note that the computation of $\cos\theta$ is approximate because it assumes small deformation and that

$\|dx\| = \|dX\| \hspace{5mm} and \hspace{5mm} \|dy\| = \|dY\|$

Symmetry of the Strain Tensor:

The symmetry of the infinitesimal strain matrix implies that there is a coordinate system in which the strain matrix is diagonal. The eigenvalues of the strain matrix are called the principal strains. If an orthonormal coordinate system aligned with the eigenvectors is chosen for the basis set, then the strain matrix is diagonal (no shear strains). In other words, in this coordinate system, no shear strains exist on the planes perpendicular to the basis vectors.

EXAMPLE:

The example shown above is repeated. In the first row, the tool draws the original shape and the deformed shape showing the deformation of the original coordinate system. In the second row, the tool draws the original shape of a small square aligned with the eigenvectors of the strain matrix which are drawn in blue and red. Notice that the square deforms into a rectangle (i.e., no shear strain!). The new rectangle might be slightly rotated as the deformation in this case is decomposed into an infinitesimal stretch described by $\varepsilon$ and an infinitesimal rotation described by $W_{inf}$ . You can vary the components $a_{ij}$ to investigate their effect on the deformed shape. Which components control the stretch and which components control the rotation?

Calculating Volumetric Strains:

For small deformations, the diagonal components of the strain matrix can be used to calculate the volumetric strain as follows:

$\frac{V-V_0}{V_0} = \varepsilon_{11} + \varepsilon_{22} + \varepsilon_{33} = Trace(\varepsilon)$

where $V$ and $V_0$ are the deformed and original volumes of a small element inside the deformed object.

Behaviour Under Pure Rotations:

A major disadvantage of the infinitesimal strain matrix is that it predicts strains for bodies that undergo large rotations even when the actual strain is zero. For example, consider a two dimensional displacement described by the rotation matrix:

$Q = \begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \\ \end{pmatrix}$

i.e.,

$x = QX$

Then, the displacement vector at every point is described by:

$u = x - X = (Q-I)X$

The gradient of displacement matrix is given by:

$\nabla u = Q - I$

The infinitesimal strain matrix is then given by:

$\varepsilon = (\frac{(Q-I)^{T} + (Q-I)}{2}) = \frac{1}{2}(Q+Q^{T}-2I) = \begin{pmatrix} \cos\theta -1 & 0 \\ 0 & \cos\theta -1 \\ \end{pmatrix} \neq 0$

For small values of $\theta, \varepsilon\simeq 0$ . However, at larger values of rotation, the strain matrix will predict high strains even though the object rotating is not being stretched. The value $\cos{\theta}-1$ for the compressive strain in the direction of the basis vectors $e_1$ and $e_2$ should not come as a surprise. If a square of unit length rotates with an angle $\theta, \cos{\theta}-1$ is actually the length of the projections of the square’s sides onto the coordinate axis!

Green Strain Tensor:

The Green strain tensor is $\varepsilon_{Green}$ is defined as follows:

$\varepsilon_{Green}= \frac{1}{2}(F^TF-I)$

By utilizing the relationship $\nabla u = F-I$ , we can replace $F$ to obtain the relationship:

$\varepsilon_{Green}= \frac{1}{2}((\nabla u + I)^T(\nabla u + I)-I)=\frac{1}{2}\left(\nabla u^T+\nabla u + \nabla u^T\nabla u\right)$

In component form, the Green strain tensor components can be written as:

$\varepsilon_{ij}=\frac{1}{2}\left( \frac{\partial u_j}{\partial X_i} + \frac{\partial u_i}{\partial X_j} + \sum\limits_{k=1}^3 {\frac{\partial u_k}{\partial X_j}\frac{\partial u_k}{\partial X_i}} \right)$

Similar to the small strain tensor, the Green strain tensor is symmetric, i.e., there is a coordinate system in which the strain matrix has diagonal components.

Calculating Longitudinal Green Strains Along General Vectors:

The Green strain tensor can be used to calculate the uniaxial (longitudinal) Green strain along general vectors. Let $dX$ be a vector in the reference configuration and $dx$ be its deformed image, then the Green strain along $dX$ can be calculated as follows:

$\varepsilon_{\mbox{Green along }dX}=\frac{1}{2}\frac{dx\cdot dx - dX\cdot dX}{\|dX\|^2}$

Utilizing the relationship $dx=FdX$ we get:

$\varepsilon_{\mbox{Green along }dX}=\frac{1}{2}\frac{FdX \cdot FdX - dX\cdot dX}{\|dX\|^2}=\frac{1}{2}\frac{dX\cdot F^TFdX - dX\cdot dX}{\|dX\|^2}=\frac{dX\cdot \frac{1}{2}(F^TF-I)dX }{\|dX\|^2}$

Therefore:

$\varepsilon_{\mbox{Green along }dX}=\frac{dX\cdot \varepsilon_{Green} dX }{\|dX\|^2}$

Calculating Change of the Dot Product Between General Vectors:

Similarly, given two vectors $dX$ and $dY$ before deformation and their respective images $dx$ and $dy$ after deformation, half the difference between the dot product in the deformed configuration and the dot product in the reference configuration can be calculated using the Green strain tensor as follows:

$\frac{1}{2}\frac{dx\cdot dy - dX\cdot dY}{\|dX\|\|dY\|}=\frac{dX\cdot \varepsilon_{Green} dY }{\|dX\|\|dY\|}$

Behaviour Under Pure Rotations:

One of the major advantages of the Green strain tensor is that it predicts zero strain in the cases of pure rotation. Assuming that a deformation is described by a rotation matrix $Q$ , i.e.: $x=QX$ . Then, the Green strain tensor is calculated as follows:

$\varepsilon_{Green}= \frac{1}{2}(F^TF-I)=\frac{1}{2}(Q^TQ-I)=\frac{1}{2}(I-I)=0$

i.e., under pure rotations, the Green strain matrix has zero components!

Eigenvectors:

The eigenvectors of the Green strain matrix stay perpendicular to each other after deformation. This can be shown as follows. Let $v_1$ and $v_2$ be two distinct eigenvectors of $\varepsilon_{Green}$ . Since $\varepsilon_{Green}$ is symmetric, then $v_1\cdot v_2=0$ . After deformation we have:

$Fv_1 \cdot F v_2 = v_1\cdot F^TF v_2 = v_1\cdot \left(2\varepsilon_{Green}+I\right)v_2=v_1\cdot 2\varepsilon_{Green}v_2+ v_1\cdot v_2$

However, since $v_2$ is an eigenvector of $\varepsilon_{Green}$ , then there exists a real number $\lambda_2$ such that $2\varepsilon_{Green}v_2=\lambda_2v_2$ . Therefore:

$Fv_1 \cdot F v_2 = 2v_1\cdot \lambda_2v_2+ v_1\cdot v_2=(2\lambda_2+1)(v_1\cdot v_2)$

Since $v_1\cdot v_2=0$ we have:

$Fv_1 \cdot F v_2 =(2\lambda_2+1)(v_1\cdot v_2) = 0$

This is not necessarily true for the eigenvectors of the small strain matrix. You can find a counter example for the small strain matrix using the following tool!

EXAMPLE:

The above example is repeated but with higher ranges of the components $a_{ij}$ to account for larger deformations. In the first row, the square and its deformed shape are shown. In the second row, a square aligned with the eigenvectors of the small strain matrix is drawn along with its image. In the third row, a square aligned with the eigenvectors of the Green strain matrix is drawn along with its image. Vary the components $a_{ij}$ and try to answer the following:

At what values of 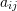$a_{ij}$ do the Green strain matrix and the small strain matrix have similar or different values?
What happens to the eigenvectors of the small strain matrix at higher rotations? Are they still perpendicular to each other after deformation?
What happens to the eigenvectors of the Green strain matrix at higher rotations? Are they still perpendicular to each other after deformation?

Open Educational Resources

Strain Measures: Three-Dimensional Strain Measures

Learning Outcomes

Three Dimensional Strain Measures

Small (Infinitesimal) Strain Tensor

Calculating Longitudinal Strains Along General Vectors:

Calculating Longitudinal Strains Along the Basis Vectors:

Calculating Angle Change Between General Vectors:

Calculating Engineering Shear Strain in the Planes of the Basis Vectors:

EXAMPLE:

Symmetry of the Strain Tensor:

EXAMPLE:

Calculating Volumetric Strains:

Behaviour Under Pure Rotations:

Green Strain Tensor:

Calculating Longitudinal Green Strains Along General Vectors:

Calculating Change of the Dot Product Between General Vectors:

Behaviour Under Pure Rotations:

Eigenvectors:

EXAMPLE:

Video

Quiz 15 – Strain Measures

Solution Guide

Leave a Reply Cancel reply