Open Educational Resources

Plane Beam Approximations: Examples and Problems

Example 1: Euler Bernoulli Simple Beam

Find the deflection, rotation, bending moment, and shearing force as a function of the beam length of an Euler Bernoulli simple beam assuming L=1 units, q=-1 units and EI=1 unit.

Solution

The DSolve function in Mathematica is used to solve the differential equation of equilibrium with four boundary conditions M=0 and y=0 on both the left and right ends of the beam.

Example1Beam

View Mathematica Code

Clear[a,x,V,M,y,L,EI]
M=EI*D[y[x],{x,2}];
V=EI*D[y[x],{x,3}];
th=D[y[x],x];
q=-a;
M1=M/.x->0;
M2=M/.x->L;
V1=V/.x->0;
V2=V/.x->L;
y1=y[x]/.x->0;
y2=y[x]/.x->L;
th1=th/.x->0;
th2=th/.x->L;
s=DSolve[{EI*y''''[x]==q,M1==0,M2==0,y1==0,y2==0},y,x];
y=y[x]/.s[[1]];
th=D[y,x];
M=EI*D[y,{x,2}];
V=EI*D[y,{x,3}];
y/.x->L/2
EI=1;
a=1;
L=1;
Plot[y,{x,0,L},BaseStyle->Directive[Bold,15],PlotRange->All,AxesLabel->{"x","y"},PlotStyle->{Black,Thickness[0.005]}]
Plot[M,{x,0,L},PlotRange->All,BaseStyle->Directive[Bold,15],AxesLabel->{"x","M"},PlotStyle->{Black,Thickness[0.005]}]
Plot[V,{x,0,L},BaseStyle->Directive[Bold,15],PlotRange->All,AxesLabel->{"x","V"},PlotStyle->{Black,Thickness[0.005]}]
Plot[th,{x,0,L},PlotRange->All,BaseStyle->Directive[Bold,15],AxesLabel->{"x","th"},PlotStyle->{Black,Thickness[0.005]}]

View Python Code

from sympy import *
from numpy import *
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
sp.init_printing(use_latex = "mathjax")
a, L, x , EI = symbols("a L x EI")
q = -a
fig, ax = plt.subplots(2,2, figsize = (10,6))
plt.setp(ax[0,0], xlabel = "x", ylabel = "y")
plt.setp(ax[0,1], xlabel = "x", ylabel = "M")
plt.setp(ax[1,1], xlabel = "x", ylabel = "th")
plt.setp(ax[1,0], xlabel = "x", ylabel = "V")
y = Function("y")
th = y(x).diff(x)
M = EI * y(x).diff(x,2)
V = EI * y(x).diff(x,3)
M1 = M.subs(x,0)
M2 = M.subs(x,L)
V1 = V.subs(x,0)
V2 = V.subs(x,L)
y1 = y(x).subs(x,0)
y2 = y(x).subs(x,L)
s = dsolve(EI*y(x).diff(x,4)-q, y(x),ics={M1/EI:0,M2/EI:0,y1:0,y2:0})
y = s.rhs
th = y.diff(x)
M = EI * y.diff(x,2)
V = EI * y.diff(x,3)
x1 = np.arange(0,1.1,0.1)
y = y.subs({L:1, a:1, EI:1})
y_list = [y.subs({x:i}) for i in x1]
th = th.subs({L:1, a:1, EI:1})
th_list = [th.subs({x:i}) for i in x1]
M = M.subs({L:1, a:1, EI:1})
M_list = [M.subs({x:i}) for i in x1]
V = V.subs({L:1, a:1, EI:1})
V_list = [V.subs({x:i}) for i in x1]
ax[0,0].plot(x1, y_list)
ax[0,1].plot(x1, M_list)
ax[1,0].plot(x1, V_list)
ax[1,1].plot(x1, th_list)

Example 2: Timoshenko Simple Beam

Find the deflection, rotation, bending moment, and shearing force as a function of the beam length of a Timoshenko simple beam assuming L=1 units, q=-1 units, kAG=1 unit and EI=1 unit.

SOLUTION

The DSolve function in Mathematica is used to solve the differential equation of equilibrium with four boundary conditions M=0 and y=0 on both the left and right ends of the beam.

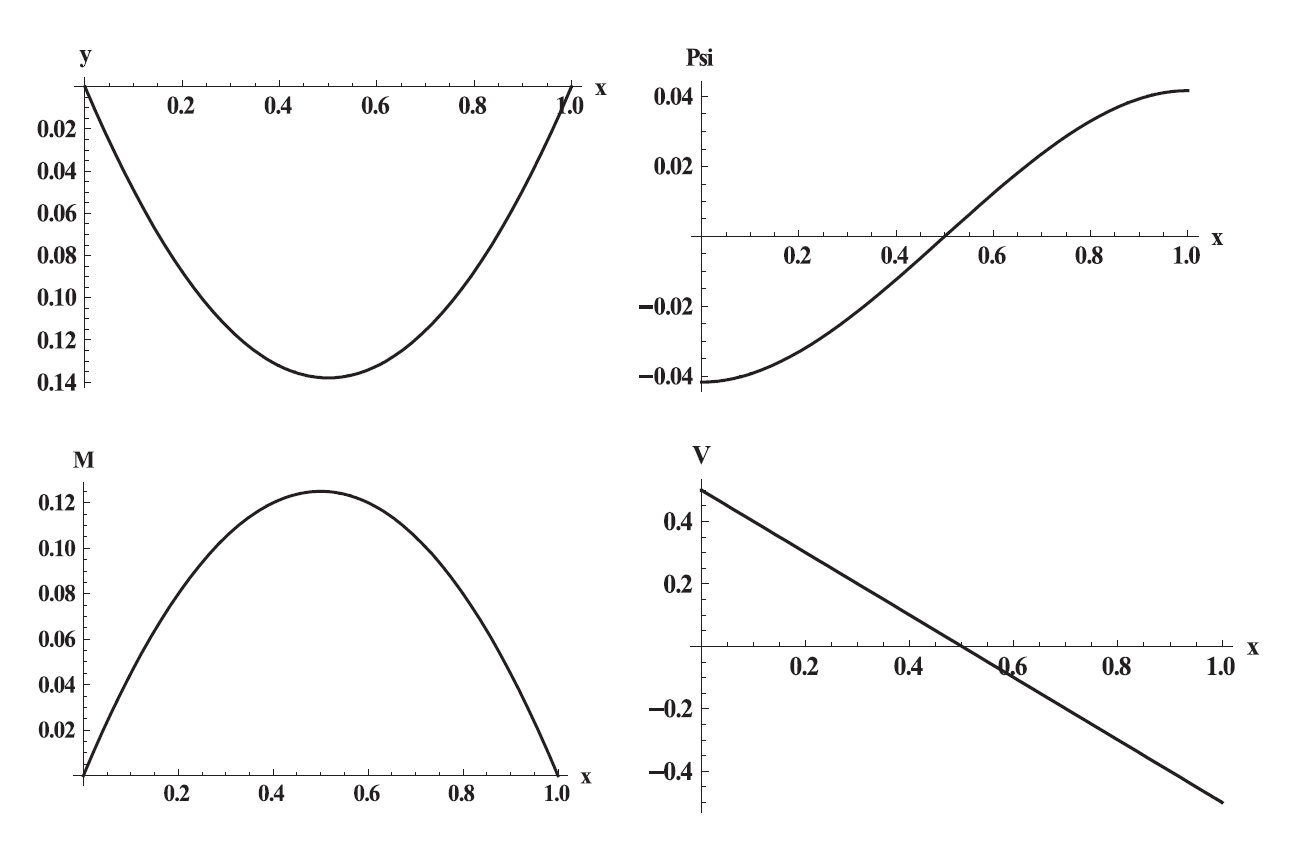
Example2Beam

View Mathematica Code

Clear[a, x, V, M, y, L, psi, EI, kAG]
M = EI*D[psi[x], x];
V = EI*D[psi[x], {x, 2}];
q = -a;
M1 = M /. x -> 0;
M2 = M /. x -> L;
V1 = V /. x -> 0;
V2 = V /. x -> L;
y1 = y[x] /. x -> 0;
y2 = y[x] /. x -> L;
psi1 = psi[x] /. x -> 0;
psi2 = psi[x] /. x -> L;
s = DSolve[{EI*psi'''[x] == q, psi[x] == y'[x] + EI/kAG*psi''[x], 
    M1 == 0, M2 == 0, y1 == 0, y2 == 0}, {y, psi}, x];
y = y /. s[[1, 2]];
psi = psi /. s[[1, 1]];
y[L/2]
EI = 1;
a = 1;
L = 1;
kAG = 1;
Plot[y[x], {x, 0, L}, BaseStyle -> Directive[Bold, 15], 
 PlotRange -> All, AxesLabel -> {"x", "y"}, 
 PlotStyle -> {Black, Thickness[0.005]}]
Plot[psi[x], {x, 0, L}, PlotRange -> All, 
 BaseStyle -> Directive[Bold, 15], AxesLabel -> {"x", "Psi"}, 
 PlotStyle -> {Black, Thickness[0.005]}]
Plot[M, {x, 0, L}, PlotRange -> All, BaseStyle -> Directive[Bold, 15],
  AxesLabel -> {"x", "M"}, PlotStyle -> {Black, Thickness[0.005]}]
Plot[V, {x, 0, L}, PlotRange -> All, BaseStyle -> Directive[Bold, 15],
  AxesLabel -> {"x", "V"}, PlotStyle -> {Black, Thickness[0.005]}]

View Python Code

from sympy import *
from numpy import *
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
sp.init_printing(use_latex = "mathjax")
a, L, x , EI, psi, kAG, C1, C2, C3, C4 = symbols("a L x EI psi kAG C_1 C_2 C_3 C_4")
q = -a
fig, ax = plt.subplots(2,2, figsize = (10,6))
plt.setp(ax[0,0], xlabel = "x", ylabel = "y")
plt.setp(ax[0,1], xlabel = "x", ylabel = "Psi")
plt.setp(ax[1,0], xlabel = "x", ylabel = "M")
plt.setp(ax[1,1], xlabel = "x", ylabel = "V")

# With general integration
EIpsi = integrate(q,x,x,x) + C1*x**2/2 + C2*x + C3 
display(EIpsi)
EIy = integrate(q,x,x,x,x) + C1*x**3/6 + C2*x**2/2 + C3*x + C4 - EI/kAG*(integrate(q,x,x) + C1*x) 
display(EIy)
M = EIpsi.diff(x)
V = EIpsi.diff(x,2)
display(M,V)
M1 = M.subs(x,0)
M2 = M.subs(x,L)
y1 = (EIy/EI).subs(x,0)
y2 = (EIy/EI).subs(x,L)
display(M1,M2,y1,y2)
s = solve([M1,M2,y1,y2], [C1, C2, C3, C4])
display(s)
x1 = np.arange(0,1.1,0.1)
EIpsi = EIpsi.subs({C1:s[C1], C2:s[C2], C3:s[C3], C4:s[C4], a:1, L:1, kAG:1, EI:1})
psi_list = [EIpsi.subs({x:i}) for i in x1]
display(EIpsi)
EIy = EIy.subs({C1:s[C1], C2:s[C2], C3:s[C3], C4:s[C4], a:1, L:1, kAG:1, EI:1})
y_list = [EIy.subs({x:i}) for i in x1]
display(EIy)
M = M.subs({C1:s[C1], C2:s[C2], C3:s[C3], a:1, L:1, kAG:1, EI:1})
M_list = [M.subs({x:i}) for i in x1]
display(M)
V = V.subs({C1:s[C1], C2:s[C2], C3:s[C3], a:1, L:1, kAG:1, EI:1})
V_list = [V.subs({x:i}) for i in x1]
display(V)
ax[0,0].plot(x1, y_list)
ax[0,1].plot(x1, psi_list)
ax[1,0].plot(x1, M_list)
ax[1,1].plot(x1, V_list)

Example 3: Bending and Shear Stresses in an Euler Brnoulli Cantilever Beam

Consider a cantilever Euler Bernoulli beam with Young’s modulus E=20 GPa. The beam is 5m long and has a rectangular cross section. The height of the beam is 0.5m, while the width is 0.25m.
If a load of 125kN is applied downwards at the free end, draw the contour plot of \sigma_{11}, \sigma_{12}, \sigma_{vM} along the beam. Also, sketch the principal stress directions at the top fibers, the bottom fibers, the neutral axis and at quarter of the height of the beam at the support X_1=0. Also, draw the vector plot of the displacement of the beam.

SOLUTION

The first step is to solve for the beam deflection by solving the differential equation of equilibrium with q=0:

    \[EI\frac{\mathrm{d}^4y}{\mathrm{d}X_1^4}=q=0\Rightarrow y=C_1\frac{X_1^3}{6}+C_2\frac{X_1^2}{2}+C_3X_1+C_4\]

where I=\frac{bt^3}{12} is the moment of inertia and b and t are given. The constants C_i can be solved using the boundary conditions:

    \[\begin{split}@X_1=0 & :y=0\\@X_1=0 & :\theta=\frac{\mathrm{d}y}{\mathrm{d}X_1}=0\\@X_1=5 & :V=EI\frac{\mathrm{d}^3y}{\mathrm{d}X_1^3}=125\\@X_1=5 & :M=EI\frac{\mathrm{d}^2y}{\mathrm{d}X_1^2}=0\end{split}\]

Therefore, the displacement function y is:

    \[y=\frac{-125}{6EI}(3LX_1^2-X_1^3)\]

From which the moment and the shear can be obtained as:

    \[M=EI\frac{\mathrm{d}^2y}{\mathrm{d}X_1^2}=125(X_1-5) kN.m.\qquad V=EI\frac{\mathrm{d}^3y}{\mathrm{d}X_1^3}=125 kN\]

The stresses along the beam length and depth can be obtained as functions of X_1 and X_2 as follows:

    \[\sigma_{11}=\frac{-MX_2}{I}=-\frac{125(X_1-5)X_2}{I}\qquad \sigma_{12}=\frac{-VQ}{Ib}=-\frac{125\left(\frac{t}{2}-X_2\right)\left(\frac{X_2}{2}+\frac{t}{4}\right)}{I}\]

the vector of displacement of the beam is given by:

    \[u=x-X=\left(\begin{array}{c}-X_2\frac{\mathrm{d}y}{\mathrm{d}X_1}\\y\\0\end{array}\right)\]

The required plots are shown below.

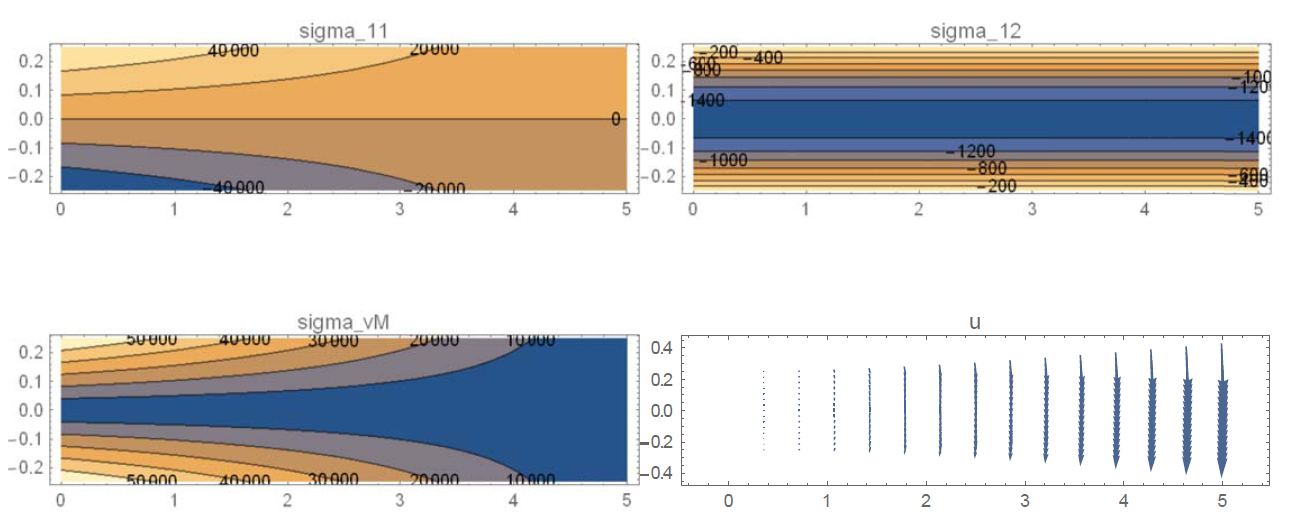
Example3Beam

As shown in the plots, the bending stress \sigma_{11} is positive at the top (tension) and negative at the bottom, and increases in magnitude towards the support. The shearing stress component \sigma_{12} is constant at the neutral axis (Why?) throughout the length of the beam and decreases toward zero at the top and bottom fibers of the beam. The von Mises stress distribution follows the bending stress component, but gives a positive value in tension and in compression!

The eigenvalues and the eigenvectors of the stress matrix at the specified locations are obtained using Mathematica and are sketched below. The shear stresses at the top and bottom fibers are zero, and thus, the principal stresses are aligned with the chosen orthonormal coordinate system. At the location of the neutral axis of the beam, the bending stress component \sigma_{11} is zero, and the only nonzero component is \sigma_{12}, thus, the principal stresses at the neutral axis are aligned at 45 degrees. The direction of the principal stress with the highest magnitude at X_2=0.125 m is along the vector {0.9993, –0.0374212,0}. At X_2=-0.125m, the principal stress with magnitude –30.042MPa is aligned with the vector {0.9993,0.0374212,0}.

Example3Beam2

View Mathematica Code

Clear[a,x,V,M,y,L,EI]
M=EI*D[y[x],{x,2}];
V=EI*D[y[x],{x,3}];
th=D[y[x],x];
M1=M/.x->0;
M2=M/.x->L;
V1=V/.x->0;
V2=V/.x->L;
y1=y[x]/.x->0;
y2=y[x]/.x->L;
th1=th/.x->0;
th2=th/.x->L;
s=DSolve[{EI*y''''[x]==0,M2==0,V2==125,y1==0,th1==0},y,x]
y=y[x]/.s[[1]]
EI=Ee*Ii;
u = {X2*-D[y, x], y}
M=FullSimplify[M/.s[[1]]]
V=V/.s[[1]]
Ee=20000000;
b=0.25;
t=0.5;
L=5;
Ii=b*t^3/12;
s11=-M*X2/Ii;
Q=(t/2-X2)*b*(t/4+X2/2)
s12=-V*Q/Ii/b;
smatrix={{s11,s12,0},{s12,0,0},{0,0,0}};
FullSimplify[Chop[smatrix]]//MatrixForm
VonMises[sigma_]:=Sqrt[1/2*((sigma[[1,1]]-sigma[[2,2]])^2+(sigma[[2,2]]-sigma[[3,3]])^2+(sigma[[3,3]]-sigma[[1,1]])^2+6*(sigma[[1,2]]^2+sigma[[1,3]]^2+sigma[[2,3]]^2))];
vonmisesstress=VonMises[smatrix]
ContourPlot[s11, {x, 0, 5}, {X2, -0.25, 0.25}, AspectRatio -> 0.25, ContourLabels -> True, PlotLabel -> "sigma_11"]
ContourPlot[s12, {x, 0, 5}, {X2, -0.25, 0.25}, AspectRatio -> 0.25, ContourLabels -> True, PlotLabel -> "sigma_12"]
ContourPlot[vonmisesstress, {x, 0, 5}, {X2, -0.25, 0.25}, AspectRatio -> 0.25, ContourLabels -> True, PlotLabel -> "sigma_vM"]
VectorPlot[u, {x, 0, 5}, {X2, -0.25, 0.25}, AspectRatio -> 0.25, PlotLabel -> "u"]
stressmat1=smatrix/.{x->0,X2->-0.25}
Eigensystem[stressmat1]
stressmat2=smatrix/.{x->0,X2->-0.25/2}
Eigensystem[stressmat2]
stressmat3=smatrix/.{x->0,X2->0}
Eigensystem[stressmat3]
stressmat4=smatrix/.{x->0,X2->0.25/2}
Eigensystem[stressmat4]
stressmat5=smatrix/.{x->0,X2->0.25}
Eigensystem[stressmat5]
stressmat1=smatrix/.{x->1,X2->-0.25}
Eigensystem[stressmat1]
stressmat2=smatrix/.{x->1,X2->-0.25/2}
Eigensystem[stressmat2]
stressmat3=smatrix/.{x->1,X2->0}
Eigensystem[stressmat3]
stressmat4=smatrix/.{x->1,X2->0.25/2}
Eigensystem[stressmat4]
stressmat5=smatrix/.{x->1,X2->0.25}
Eigensystem[stressmat5]

View Python Code

from sympy import *
from numpy import *
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
sp.init_printing(use_latex = "mathjax")
x , EI, X2, L, I, t, E= symbols("x EI X_2 L I t Ee")

def vonMises(M):
    return sp.sqrt(1/2*((M[0,0] - M[1,1])**2+(M[1,1] - M[2,2])**2+
                       (M[2,2] - M[0,0])**2+6*(M[0,1]**2+M[0,2]**2+M[1,2]**2)))

def plotContour(f, limits, title):
    x1, xn, y1, yn = limits
    dx, dy = 10/100*(xn-x1),10/100*(yn - y1)
    xrange = np.arange(x1,xn+dx,dx)
    yrange = np.arange(y1,yn+dy,dy)
    X, Y = np.meshgrid(xrange, yrange)
    lx, ly = len(xrange), len(yrange)
    F = lambdify((x,X2),f)
    # if F is constant, then generates array
    # if F generates array, doesn't change anything
    Z = F(X,Y)*np.ones(lx*ly).reshape(lx, ly)
    fig = plt.figure(figsize = (8,2))
    ax = fig.add_subplot(111)
    cp = ax.contourf(X,Y,Z)
    fig.colorbar(cp)
    plt.title(title)

def plotVector(f, limits, title):
    fx, fy = [lambdify((x,X2),fi) for fi in f]
    x1, xn, y1, yn = limits
    dx, dy = 10/100*(xn-x1),10/100*(yn-y1)
    xrange = np.arange(x1,xn,dx)
    yrange = np.arange(y1,yn,dy)
    X, Y = np.meshgrid(xrange, yrange)
    dxplot, dyplot = fx(X,Y), fy(X,Y)
    fig = plt.figure(figsize = (7.5,2))
    ax = fig.add_subplot(111)
    ax.quiver(X, Y, dxplot, dyplot)
    plt.title(title)

y = Function('y')
th = y(x).diff(x)
M = EI * y(x).diff(x,2)
V = EI * y(x).diff(x,3)
M1 = M.subs(x,0)
M2 = M.subs(x,L)
V1 = V.subs(x,0)
V2 = V.subs(x,L)
y1 = y(x).subs(x,0)
y2 = y(x).subs(x,L)
th1 = th.subs(x,0)
th2 = th.subs(x,L)
s = dsolve(EI*y(x).diff(x,4), y(x), ics = {M2/EI:0,V2/EI:125/EI,y1:0, th1:0})
display("displacement function: ",s)
y = s.rhs
u = Matrix([[X2* -y.diff(x)], [y]])
M = EI * y.diff(x,2)
V = EI * y.diff(x,3) 
display("Moment: ", M.subs(L,5))
display("Shear: ", V)
s11 = -M*X2/I
b = 0.25
Q = (t/2 - X2) * b * (t/4 + X2/2)
s12 = -V * Q/I/b
display("stresses: ", s11, s12)
s11 = s11.subs({E:20000000, t:0.5, L:5, I:b*t**3/12})
s12 = s12.subs({E:20000000, t:0.5, L:5, I:b*t**3/12})
smatrix = Matrix([[s11, s12, 0], [s12, 0, 0], [0, 0, 0]])
vonMisesstress = vonMises(smatrix)
display("von Mises stress: ", vonMisesstress)
plotContour(s11, [0,5,-0.25,0.25], "sigma_11")
plotContour(s12, [0,5,-0.25,0.25], "sigma_12")
plotContour(vonMisesstress, [0,5,-0.25,0.25], "sigma_vM")
u = u.subs({E:20000000, t:0.5, L:5, Ii:b*t**3/12, EI:E*Ii})
plotVector(u, [0,5,-0.25,0.25], "u")
stressmat1 = smatrix.subs({x:0, X2: -0.25})
display("stress matrix 1 eigensystem(x = 0, X2 = -0.25): ", stressmat1.eigenvects())
stressmat2 = smatrix.subs({x:0, X2: -0.25/2})
display("stress matrix 2 eigensystem(x = 0, X2 = -0.25/2): ", stressmat2.eigenvects())
stressmat3 = smatrix.subs({x:0, X2: 0})
display("stress matrix 3 eigensystem(x = 0, X2 = 0): ", stressmat3.eigenvects())
stressmat4 = smatrix.subs({x:0, X2: 0.25/2})
display("stress matrix 4 eigensystem(x = 0, X2 = 0.25/2): ", stressmat4.eigenvects())
stressmat5 = smatrix.subs({x:0, X2: 0.25})
display("stress matrix 5 eigensystem(x = 0, X2 = 0.25): ", stressmat5.eigenvects())
stressmat1_2 = smatrix.subs({x:0, X2: -0.25})
display("stress matrix 1 eigensystem(x = 1, X2 = -0.25): ", stressmat1_2.eigenvects())
stressmat2_2 = smatrix.subs({x:1, X2: -0.25/2})
display("stress matrix 2 eigensystem(x = 1, X2 = -0.25/2): ", stressmat2_2.eigenvects())
stressmat3_2 = smatrix.subs({x:1, X2: 0})
display("stress matrix 3 eigensystem(x = 1, X2 = 0): ", stressmat3_2.eigenvects())
stressmat4_2 = smatrix.subs({x:1, X2: 0.25/2})
display("stress matrix 4 eigensystem(x = 1, X2 = 0.25/2): ", stressmat4_2.eigenvects())
stressmat5_2 = smatrix.subs({x:1, X2: 0.25})
display("stress matrix 5 eigensystem(x = 1, X2 = 0.25): ", stressmat5_2.eigenvects())

Example 4: Bending and Shear Stresses in an Euler Bernoulli Simple Beam

Consider an Euler Bernoulli simple beam with Young’s modulus E=20 GPa. The beam is 8m long and has a rectangular cross section. The height of the beam is 0.5m, while the width is 0.25m. If a load of 125kN/m is distributed over the beam length, draw the contour plot of \sigma_{11}, \sigma_{12}, and \sigma_{vM} along the beam. Also, draw the vector plot of the displacement of the beam.

SOLUTION

The first step is to solve for the beam deflection by solving the differential equation of equilibrium with q=-125:

    \[EI\frac{\mathrm{d}^4y}{\mathrm{d}X_1^4}=q=-125\Rightarrow EIy=-125\frac{X_1^4}{24}+C_1\frac{X_1^3}{6}+C_2\frac{X_1^2}{2}+C_3X_1+C_4\]

where I=\frac{bt^3}{12} is the moment of inertia and b and t are given. The constants C_i can be solved using the boundary conditions:

    \[\begin{split}@X_1=0 & :y=0\\@X_1=0 & :M=EI\frac{\mathrm{d}^2y}{\mathrm{d}X_1^2}=0\\@X_1=8 & :y=0\\@X_1=8 & :M=EI\frac{\mathrm{d}^2y}{\mathrm{d}X_1^2}=0\end{split}\]

Therefore, the displacement function y is:

    \[y=\frac{-125}{24EI}(L^3X_1-2LX_1^3+X_1^4)\]

From which the moment and the shear can be obtained as:

    \[M=EI\frac{\mathrm{d}^2y}{\mathrm{d}X_1^2}=-\frac{125X_1}{2}(X_1-8) kN.m.\qquad V=EI\frac{\mathrm{d}^3y}{\mathrm{d}X_1^3}=-125(X_1-4) kN\]

The stresses along the beam length and depth can be obtained as functions of X_1 and X_2 as follows:

    \[\sigma_{11}=\frac{-MX_2}{I}=-\frac{-\frac{125X_1}{2}(X_1-8)X_2}{I}\qquad \sigma_{12}=\frac{-VQ}{Ib}=-\frac{-125(X_1-4)\left(\frac{t}{2}-X_2\right)\left(\frac{X_2}{2}+\frac{t}{4}\right)}{I}\]

the vector of displacement of the beam is given by:

    \[u=x-X=\left(\begin{array}{c}-X_2\frac{\mathrm{d}y}{\mathrm{d}X_1}\\y\\0\end{array}\right)\]

The required plots are shown below.

BeamExample4

As shown in the contour plots, the contribution of the shear stresses \sigma_{12} in \sigma_{vM} in this beam is very small compared to the bending stress \sigma_{11}. This is natural due to the small ratio between the depth of the beam and its length. The longer the beam, the less significant the shear stresses are. The following is the Mathematica code utilized for the above calculations.

View Mathematica Code

Clear[a,x,V,M,y,L,EI,Ee,Ii]
M=EI*D[y[x],{x,2}];
V=EI*D[y[x],{x,3}];
th=D[y[x],x];
q=-125;
M1=M/.x->0;
M2=M/.x->L;
V1=V/.x->0;
V2=V/.x->L;
y1=y[x]/.x->0;
y2=y[x]/.x->L;
th1=th/.x->0;
th2=th/.x->L;
s=DSolve[{EI*y''''[x] ==q,M2==0,y2==0,y1==0,M1==0},y,x]
y=y[x]/.s[[1]]
EI=Ee*Ii;
u={X2*-D[y,x],y}
L=8;
M=FullSimplify[M/.s[[1]]]
V=FullSimplify[V/.s[[1]]]
Ee=20000000;
b=0.25;
t=0.5;
Ii=b*t^3/12;
s11=-M*X2/Ii
Q=(t/2-X2)*b*(t/4+X2/2)
s12=-V*Q/Ii/b
smatrix={{s11,s12,0},{s12,0,0},{0,0,0}};
FullSimplify[Chop[smatrix]]//MatrixForm
VonMises[sigma_]:=Sqrt[1/2*((sigma[[1,1]]-sigma[[2,2]])^2+(sigma[[2,2]]-sigma[[3,3]])^2+(sigma[[3,3]]-sigma[[1,1]])^2+6*(sigma[[1,2]]^2+sigma[[1,3]]^2+sigma[[2,3]]^2))];
vonmisesstress=VonMises[smatrix]
ContourPlot[s11,{x,0,L},{X2,-0.25,0.25},AspectRatio->0.25,ContourLabels->True,PlotLabel->"Sigma_11"]
ContourPlot[s12,{x,0,L},{X2,-0.25,0.25},AspectRatio->0.25,ContourLabels->True,PlotLabel->"Sigma_12"]
ContourPlot[vonmisesstress,{x,0,L},{X2,-0.25,0.25},AspectRatio->0.25,ContourLabels->True,PlotLabel->"Sigma_vM"]
VectorPlot[u,{x,0,L},{X2,-0.25,0.25},AspectRatio->0.25,PlotLabel->"Displacement Vector"]

View Python Code

from sympy import *
from numpy import *
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
sp.init_printing(use_latex = "mathjax")
a, L, x , EI, E,  I  = symbols("a L x EI Ee I")

def vonMises(M):
    return sp.sqrt(1/2*((M[0,0] - M[1,1])**2+(M[1,1] - M[2,2])**2+
                       (M[2,2] - M[0,0])**2+6*(M[0,1]**2+M[0,2]**2+M[1,2]**2)))

def plotContour(f, limits, title):
    x1, xn, y1, yn = limits
    dx, dy = 10/100*(xn-x1),10/100*(yn - y1)
    xrange = np.arange(x1,xn+dx,dx)
    yrange = np.arange(y1,yn+dy,dy)
    X, Y = np.meshgrid(xrange, yrange)
    lx, ly = len(xrange), len(yrange)
    F = lambdify((x,X2),f)
    # if F is constant, then generates array
    # if F generates array, doesn't change anything
    Z = F(X,Y)*np.ones(lx*ly).reshape(lx, ly)
    fig = plt.figure(figsize = (8,2))
    ax = fig.add_subplot(111)
    cp = ax.contourf(X,Y,Z)
    fig.colorbar(cp)
    plt.title(title)

def plotVector(f, limits, title):
    fx, fy = [lambdify((x,X2),fi) for fi in f]
    x1, xn, y1, yn = limits
    dx, dy = 10/100*(xn-x1),10/100*(yn-y1)
    xrange = np.arange(x1,xn,dx)
    yrange = np.arange(y1,yn,dy)
    X, Y = np.meshgrid(xrange, yrange)
    dxplot, dyplot = fx(X,Y), fy(X,Y)
    fig = plt.figure(figsize = (7.5,2))
    ax = fig.add_subplot(111)
    ax.quiver(X, Y, dxplot, dyplot)
    plt.title(title)

y = Function('y')
th = y(x).diff(x)
M = EI * y(x).diff(x,2)
V = EI * y(x).diff(x,3)
q = -125
M1 = M.subs(x,0)
M2 = M.subs(x,L)
V1 = V.subs(x,0)
V2 = V.subs(x,L)
y1 = y(x).subs(x,0)
y2 = y(x).subs(x,L)
th1 = th.subs(x,0)
th2 = th.subs(x,L)
s = dsolve(EI*y(x).diff(x,4) - q, y(x), ics = {M2/EI:0,y1:0,y2:0, M1/EI:0})
display("displacement function: ",s)
y = s.rhs
u = Matrix([[X2* -y.diff(x)], [y]])
M = EI * y.diff(x,2)
V = EI * y.diff(x,3) 
display("Moment: ", M.subs(L,8))
display("Shear: ", V.subs(L,8))
b = 0.25
s11 = -M*X2/I
Q = (t/2 - X2) * b * (t/4 + X2/2)
s12 = -V * Q/I/b
display("stresses: ", s11.subs(L,8), s12.subs(L,8))
s11 = s11.subs({E:20000000, t:0.5, L:8, I:b*t**3/12})
s12 = s12.subs({E:20000000, t:0.5, L:8, I:b*t**3/12})
smatrix = Matrix([[s11, s12, 0], [s12, 0, 0], [0, 0, 0]])
vonMisesstress = vonMises(smatrix)
display("von Mises stress: ", vonMisesstress)
plotContour(s11, [0,8,-0.25,0.25], "sigma_11")
plotContour(s12, [0,8,-0.25,0.25], "sigma_12")
plotContour(vonMisesstress, [0,8,-0.25,0.25], "sigma_vM")
u = u.subs({E:20000000, t:0.5, L:8, I:b*t**3/12, EI:E*I})
plotVector(u, [0,8,-0.25,0.25], "Displacement Vector")

Example 5: Beam Under Axial Load with Displacement Boundary Conditions

A beam fixed at both ends is under a triangular axial load with a maximum value of 125 kN/m at X_1= L. The beam’s length, width, and height are 5, 0.25, and 0.5 m, respectively. Young’s modulus is 20 GPa. Ignore the effect of Poisson’s ratio. Find the displacement function of this beam along with the stress distribution along the length of the beam. Draw the contour plot of \sigma_{11} and the vector plot of the displacement along the beam.

Axial1
SOLUTION

The displacement vector function of the beam has the form:

    \[u=\left(\begin{array}{c}u_1(X_1)\\0\\0\end{array}\right)\]

The only nonzero strain component is \varepsilon_{11}:

    \[\varepsilon_{11}=\frac{\mathrm{d}u_1}{\mathrm{d}X_1}\]

Ignoring the effect of Poisson’s ratio, the only nonzero stress component is \sigma_{11}:

    \[\sigma_{11}=E\varepsilon_{11}=E\frac{\mathrm{d}u_1}{\mathrm{d}X_1}\]

The distributed axial load follows the equation:

    \[p=125\frac{X_1}{L}\]

The equilibrium equation (Equation 12) for beams under axial loading can be used with constant EA to write:

    \[EA\frac{\mathrm{d}^2u_1}{\mathrm{d}X_1^2}=-125\frac{X_1}{L}\]

The boundary conditions are:

    \[\begin{split}@X_1=0 & :u_1=0\\@X_1=L & :u_1=0\end{split}\]

Therefore, the solution to the above ordinary differential equation yields the following forms for u_1, \sigma_{11}, and the normal force N=\sigma_{11}A:

    \[u_1=\frac{125(X_1L^2-X_1^3)}{6EAL}\qquad \sigma_{11}=\frac{125(L^2-3X_1^2)}{6AL}\qquad N=\frac{125(L^2-3X_1^2)}{6L}\]

The required contour plots and the Mathematica code used are below.

AxialSolution1

View Mathematica Code

Clear[u,x,L,EA,Ee,A]
EA=Ee*A;
u1=u[x]/.x->0;
u2=u[x]/.x->L;
Normalf=EA*D[u[x]];
qnormal=125*x/L;
s=DSolve[{EA*u''[x]==-qnormal,u1==0,u2==0},u,x]
u=u[x]/.s[[1]]
s11=Ee*D[u,x]
Normalf=Normalf/.s[[1]];
Ee=20000;
A=0.25*0.5;
L=5;
disp={u,0}
ContourPlot[s11,{x,0,5},{X2,-0.25,0.25},AspectRatio->0.25,ContourLabels->True,PlotLabel->"sigma_11 (MPa)"]
VectorPlot[disp,{x,0,5},{X2,-0.25,0.25},AspectRatio->0.25,PlotLabel->"Displacement Vector"]

View Python Code

from sympy import *
from numpy import *
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
sp.init_printing(use_latex = "mathjax")
A, L, x , EA, E = symbols("A L x EA E")

def plotContour(f, limits, title):
    x1, xn, y1, yn = limits
    dx, dy = 10/100*(xn-x1),10/100*(yn - y1)
    xrange = np.arange(x1,xn+dx,dx)
    yrange = np.arange(y1,yn+dy,dy)
    X, Y = np.meshgrid(xrange, yrange)
    lx, ly = len(xrange), len(yrange)
    F = lambdify((x,X2),f)
    # if F is constant, then generates array
    # if F generates array, doesn't change anything
    Z = F(X,Y)*np.ones(lx*ly).reshape(lx, ly)
    fig = plt.figure(figsize = (8,2))
    ax = fig.add_subplot(111)
    cp = ax.contourf(X,Y,Z)
    fig.colorbar(cp)
    plt.title(title)

def plotVector(f, limits, title):
    fx, fy = [lambdify((x,X2),fi) for fi in f]
    x1, xn, y1, yn = limits
    dx, dy = 10/100*(xn-x1),10/100*(yn-y1)
    xrange = np.arange(x1,xn,dx)
    yrange = np.arange(y1,yn,dy)
    X, Y = np.meshgrid(xrange, yrange)
    dxplot, dyplot = fx(X,Y), fy(X,Y)
    fig = plt.figure(figsize = (7.5,2))
    ax = fig.add_subplot(111)
    ax.quiver(X, Y, dxplot, dyplot)
    plt.title(title)

u = Function("u")
EA = E * A
u1 = u(x).subs(x,0)
u2 = u(x).subs(x,L)
Normalf = EA * u(x).diff(x)
qnormal = 125 * x/L
display("Only non-zero stress component: ", Normalf)
display("Distributed axial Load: ", qnormal)
s = dsolve(EA * u(x).diff(x,2) + qnormal, u(x), ics = {u1:0, u2:0})
u = s.rhs
s11 = E * u.diff(x)
Normalf = EA * u.diff(x)
display("u_1, sigma_11 and Normal force: ", u, s11, Normalf)
s11 = s11.subs({E:20000, A:0.125, L:5})
u = u.subs({E:20000, A:0.125, L:5})
disp = Matrix([[u], [0]])
plotContour(s11, [0,5,-0.25,0.3], "sigma_11")
plotVector(disp, [0,5,-0.25,0.3], "Displacement Vector")

Example 6: Beam Under Axial Load with Displacement and Stress Boundary Conditions

The shown beam has one fixed end and one free end. The beam is under a triangular axial load with a maximum value of 125kN/m at X_1=L. The beam’s length, width, and height are 5, 0.25, and 0.5m, respectively. Young’s modulus is 20 GPa. Ignore the effects of Poisson’s ratio and find the displacement function of this beam along with the stress distribution. Draw the contour plots of \sigma_{11} and the vector plot of the displacement. axial 2

axial-2
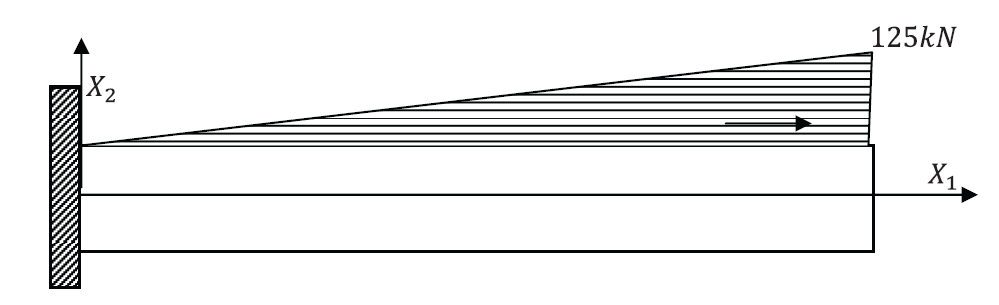
SOLUTION:

The displacement vector function of the beam has the form:

    \[u=\left(\begin{array}{c}u_1(X_1)\\0\\0\end{array}\right)\]

The only nonzero strain component is \varepsilon_{11}:

    \[\varepsilon_{11}=\frac{\mathrm{d}u_1}{\mathrm{d}X_1}\]

Ignoring the effect of Poisson’s ratio, the only nonzero stress component is \sigma_{11}:

    \[\sigma_{11}=E\varepsilon_{11}=E\frac{\mathrm{d}u_1}{\mathrm{d}X_1}\]

The distributed axial load follows the equation:

    \[p=125\frac{X_1}{L}\]

The equilibrium equation (Equation 12) for beams under axial loading can be used with constant EA to write:

    \[EA\frac{\mathrm{d}^2u_1}{\mathrm{d}X_1^2}=-125\frac{X_1}{L}\]

The boundary conditions are:

    \[\begin{split}@X_1=0 & :u_1=0\\@X_1=L & :\sigma_{11}=E\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=0\end{split}\]

Therefore, the solution to the above ordinary differential equation yields the following forms for u_1, \sigma_{11}, and the normal force N=\sigma_{11}A:

    \[u_1=\frac{125(3X_1L^2-X_1^3)}{6EAL}\qquad \sigma_{11}=\frac{125(3L^2-3X_1^2)}{6AL}\qquad N=\frac{125(3L^2-3X_1^2)}{6L}\]

The required contour plots and the Mathematica code used are below. Compare the plots with the previous example.

The required contour plots and the Mathematica code used are below.

AxialSolution2

View Mathematica Code

Clear[u,x,L,EA,Ee,A]
EA=Ee*A;
u1=u[x]/.x->0;
BC2=D[u[x],x]/.x->L;
Normalf=EA*D[u[x]];
qnormal=125*x/L;
s=DSolve[{EA*u''[x]==-qnormal,u1==0,BC2==0},u,x]
u=u[x]/.s[[1]]
s11=Ee*D[u,x]
Normalf=Normalf/.s[[1]];
Ee=20000;
A=0.25*0.5;
L=5;
disp={u,0}
ContourPlot[s11,{x,0,5},{X2,-0.25,0.25},AspectRatio->0.25,ContourLabels->True,PlotLabel->"sigma_11 (MPa)"]
VectorPlot[disp,{x,0,5},{X2,-0.25,0.25},AspectRatio->0.25,PlotLabel->"Displacement Vector"]

View Python Code

from sympy import *
from numpy import *
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
sp.init_printing(use_latex = "mathjax")
A, L, x , EA, E = symbols("A L x EA E")

def plotContour(f, limits, title):
    x1, xn, y1, yn = limits
    dx, dy = 10/100*(xn-x1),10/100*(yn - y1)
    xrange = np.arange(x1,xn+dx,dx)
    yrange = np.arange(y1,yn+dy,dy)
    X, Y = np.meshgrid(xrange, yrange)
    lx, ly = len(xrange), len(yrange)
    F = lambdify((x,X2),f)
    # if F is constant, then generates array
    # if F generates array, doesn't change anything
    Z = F(X,Y)*np.ones(lx*ly).reshape(lx, ly)
    fig = plt.figure(figsize = (8,2))
    ax = fig.add_subplot(111)
    cp = ax.contourf(X,Y,Z)
    fig.colorbar(cp)
    plt.title(title)

def plotVector(f, limits, title):
    fx, fy = [lambdify((x,X2),fi) for fi in f]
    x1, xn, y1, yn = limits
    dx, dy = 10/100*(xn-x1),10/100*(yn-y1)
    xrange = np.arange(x1,xn,dx)
    yrange = np.arange(y1,yn,dy)
    X, Y = np.meshgrid(xrange, yrange)
    dxplot, dyplot = fx(X,Y), fy(X,Y)
    fig = plt.figure(figsize = (7.5,2))
    ax = fig.add_subplot(111)
    ax.quiver(X, Y, dxplot, dyplot)
    plt.title(title)

u = Function("u")
EA = E * A
u1 = u(x).subs(x,0)
BC2 = u(x).diff(x).subs(x,L)
Normalf = EA * u(x).diff(x)
qnormal = 125 * x/L
display("Only non-zero stress component: ", Normalf)
display("Distributed axial Load: ", qnormal)
s = dsolve(EA * u(x).diff(x,2) + qnormal, u(x), ics = {u1:0, BC2:0})
u = s.rhs
s11 = E * u.diff(x)
Normalf = EA * u.diff(x)
display("u_1, sigma_11 and Normal force: ", u, s11, Normalf)
s11 = s11.subs({E:20000, A:0.125, L:5})
u = u.subs({E:20000, A:0.125, L:5})
disp = Matrix([[u], [0]])
plotContour(s11, [0,5,-0.25,0.25], "sigma_11")
plotVector(disp, [0,5,-0.25,0.25], "Displacement Vector")

Example 7: Beam Under Axial Load With Varying Cross Sectional Area

The shown beam has a varying circular cross sectional area with a radius r=2 units at the top varying linearly to r=1 unit at the bottom. The beam is used to carry a concentrated load P and has a weight density \rho. Young’s modulus E=1000 units. Find the vertical displacement field of the beam.

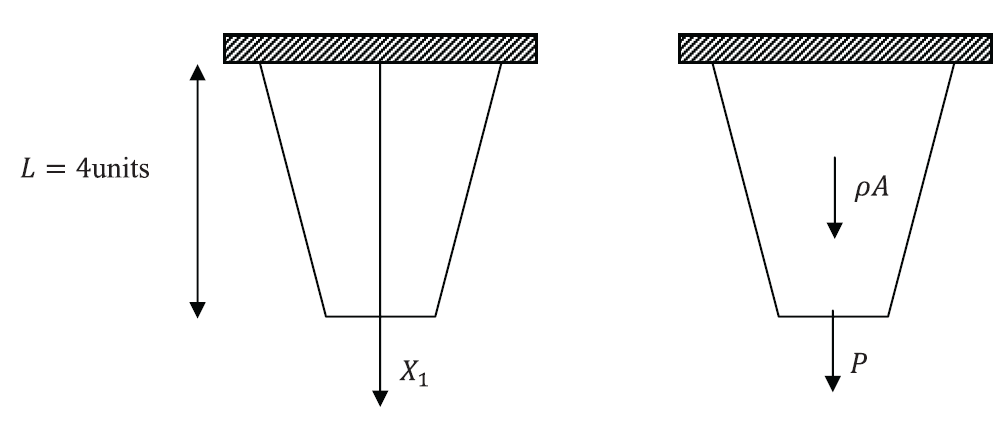
axial-3
SOLUTION:

Since the beam has a varying cross sectional area, this induces a varying vertical load due to the beam’s own weight. The radius r and the area A vary with X_1 according to the equations:

    \[r=2-\frac{X_1}{L}\qquad A=\pi\left(2-\frac{X_1}{L}\right)^2\]

Similar to the two previous examples, the only nonzero strain component is \varepsilon_{11} and ignoring Poisson’s ratio we get:

    \[\varepsilon_{11}=\frac{\mathrm{d}u_1}{\mathrm{d}X_1}\qquad \sigma_{11}=E\varepsilon_{11}=E\frac{\mathrm{d}u_1}{\mathrm{d}X_1}\]

whereu_1 is the unknown displacement component along the axis X_1. The equilibrium equation (Equation 12) for beams under axial loading can be used with varying EA to write:

    \[E\frac{\mathrm{d}A}{\mathrm{d}X_1}\frac{\mathrm{d}u_1}{\mathrm{d}X_1}+EA\frac{\mathrm{d}^2u_1}{\mathrm{d}X_1^2}+\rho A=0\]

Substituting for A in the above equation we get:

    \[E\frac{\pi}{2}\left(\frac{X_1}{4}-2\right)\frac{\mathrm{d}u_1}{\mathrm{d}X_1}+E\pi\left(2-\frac{X_1}{4}\right)^2\frac{\mathrm{d}^2u_1}{\mathrm{d}X_1^2}+\pi\rho\left(2-\frac{X_1}{4}\right)^2=0\]

The boundary conditions are:

    \[\begin{split}@X_1=0 & :u_1=0\\@X_1=L & :\sigma_{11}=E\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=\frac{P}{A}\bigg|_{X_1=L}\end{split}\]

Mathematica can be used to solve the above differential equation to find the solution for u_1 as follows:

    \[u_1=\frac{-12PX_1-112\pi\rho X_1+24 \pi\rho X_1^2-\pi\rho X_1^3}{6E\pi(X_1-8)}\]

View Mathematica Code

Clear[L,A,Al,ro,Ee,u]
L=4;
A=Pi*(2-x/L)^2;
Al=A/.x->L;
s=DSolve[{D[Ee*A*u'[x],x]+ro*A==0,u[0]==0,u'[L]==P/Ee/Al},u,x]

View Python Code

from sympy import *
from numpy import *
import sympy as sp
import numpy as np
sp.init_printing(use_latex = "mathjax")
L, x , A, Al, ro, E, u, pi, P= symbols("L x A Al rho E u pi P")
u = Function("u")
u1 = u(x).subs(x,0)
u2 = u(x).diff(x).subs(x,L)
A = pi*(2-x/L)**2
display("Area: ", A)
Al = A.subs(x,L)
s = dsolve((E*A*u(x).diff(x)).diff(x) + ro * A, u(x), ics = {u1:0, u2:P/E/Al})
display(s.subs(L, 4))

You can now copy and paste the following code into Mathematica to see the effect of changing the density and the external load on the displacement function produced for 0\leq P \leq 500 and 0\leq \rho \leq 100. What is the combination of \rho and P that would produce an almost linear displacement field?

View Mathematica Code

Clear[u,x,Ee,P,L,A]
Manipulate[Ee=1000;
L=4;
A=Pi*(2-x/L)^2;
Al=A/.x->L;
s=DSolve[{D[Ee*A*u'[x],x]+ro*A==0,u[0] ==0,u'[L] ==P/Ee/Al},u,x];
s=u/.s[[1]];
Plot[s[x],{x,0,L}],{P,0,500},{ro,0,100}]

View Python Code

%matplotlib notebook
from sympy import *
from numpy import *
import sympy as sp
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider
sp.init_printing(use_latex = "mathjax")
L, x , A, Al, ro, E, u, pi, P= symbols("L x A Al rho E u pi P")
u = Function("u")
u1 = u(x).subs(x,0)
u2 = u(x).diff(x).subs(x,L)
A = pi*(2-x/L)**2
Al = A.subs(x,L)
s = dsolve((E*A*u(x).diff(x)).diff(x) + ro * A, u(x), ics = {u1:0, u2:P/E/Al})
s = s.rhs
s = s.subs(L,4)
initial = s.subs({ro:100, P:500, E:1000, pi:np.pi})           
fig = plt.figure()
ax = fig.add_subplot(111)
x1 = np.arange(0,4.1,1)
s_list = [initial.subs({x:i}) for i in x1]
#Initial PLot
ax.plot(x1, s_list)
def Update_func(event):
    new = s.subs({ro:slider1.val, P:slider2.val, E:1000, pi:np.pi})
    newx = np.arange(0,4.1,1)
    new_s_list = [new.subs({x:i}) for i in newx]
    ax.clear()
    ax.plot(newx, new_s_list)
plt.subplots_adjust(left = 0.1, bottom = 0.45)
roslider = plt.axes([0.2,0.2,0.5,0.03])
Pslider = plt.axes([0.2,0.15,0.5,0.03])
slider1 = Slider(roslider, 'ro', 0, 100, valinit = 100, valstep = 1)
slider2 = Slider(Pslider, 'P', 0, 500, valinit = 500, valstep = 1)
slider1.on_changed(Update_func)
slider2.on_changed(Update_func)

plt.show()

Problems

  1. Use Mathematica to solve the Euler Bernoulli beam and the Timoshenko beam equations (shear, moment, rotation (slope), and deflection) for the beams shown in the following figure (assume values for the loads and material constants). Also, find the maximum deflection associated with the loads shown.
  2. Rewrite the final equations presented for the Euler Bernoulli beam and the Timoshenko beam assuming that the cross-sectional area parameters I and A are not constant.
  3. Conduct a literature search to find the values of the shear coefficient k of the Timoshenko beam for different cross-sectional shapes. (Square, circle, I beam etc.)
  4. A beam is 6m long with a rectangular cross-sectional area whose width and height are 0.25m and 0.5m, respectively. Young’s modulus is 20GPa. Ignore the effect of Poisson’s ratio. A distributed load of a value 125kN/m is applied vertically downward. Compare the following between a simple beam and a fixed-ends beam:
    1. Deflection, bending moment, and shearing force distribution along the beam.
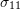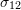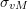    2. \sigma_{11}, \sigma_{12}, \sigma_{vM}, and the hydrostatic stress (Draw the contour plots and comment on the difference).
  5. The shown beam has a rectangular cross-sectional area with a width of 0.25m. The height of the beam varies linearly along its length as shown in the figure below. Young’s modulus is taken as 20GPa while the effect of Poisson’s ratio is ignored. Assume that the only nonzero component of the stress is 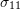\sigma_{11} and that plane sections perpendicular to the 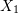X_1 axis remain plane and perpendicular to the 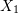X_1 axis after deformation. Find the following:
    1. A generic form for the position and the displacement functions.
    2. The expression for the infinitesimal strain tensor components.
    3. The differential equation of equilibrium and its boundary conditions.
    4. Solve the differential equation of equilibrium to find the displacement of the beam at every point.
    5. Draw the contour plots of \sigma_{11}.
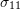    6. Draw the vector plot of the displacement vector u=\left(\begin{array}{c}u_1\\u_2\end{array}\right).
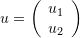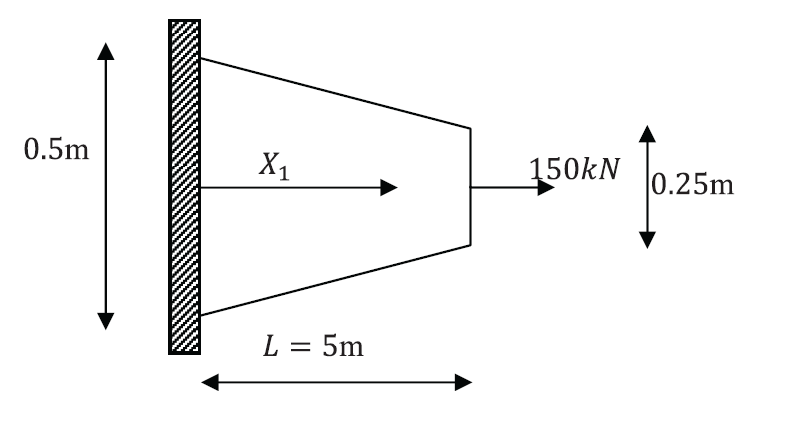
    ExampleBeam2
  6. The shown beam structure has a circular cross sectional area with radius of 2m at the bottom varying linearly to 1m at the top. The length of the structure is 4m. A crane is used to carry it from the top. Consider the weight density of the member as 10 N/m^3 and Young’s modulus of 1000 N/m^2. Ignore Poisson’s ratio and assume that the only nonzero component of the stress is the normal stress in the vertical direction and that it is uniformly distributed in the cross section. Find the displacement function of the beam, the total elongation or contraction, and the distribution of the nonzero normal stress component in the following cases:
    1. When the beam is resting on the ground.
    2. When the crane is carrying half the weight of the beam but the bottom of the beam is still on the ground.
    3. When the beam is suspended in the air.
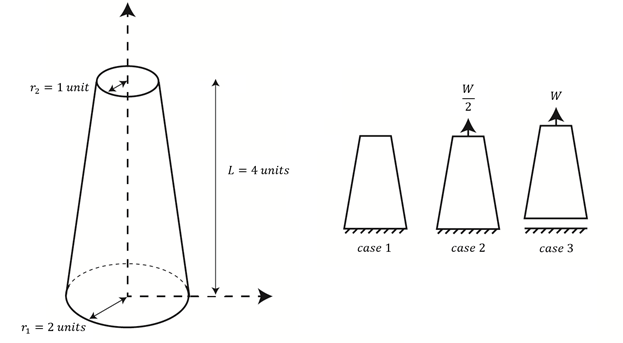
    beamproblem
  7. A cantilever beam with a rectangular cross section is subjected to a uniformly distributed load. The length of the beam is 5 m, its width and height are respectively 400 mm and 500 mm and the distributed load is equal to 15 KN/m. A rigid block is located under the free end of the beam and a gap equal to 10 mm exists between the free end and the rigid block. Consider the Young’s modulus as 20 GPa and find the following:
    1. the reaction force of the rigid block.
    2. the deflection of the neutral axis of the beam.
    3. the displacement field inside the beam.
    4. the stress component 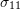\sigma_{11} inside the beam. Draw the contour plots of \sigma_{11}.

Page Comments

  1. Nikolaj Dagnæs says:
    February 15, 2024 at 11:39 pm

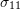    This is educational ressources of highest quality. Good job.

    Reply

Leave a Reply

Your email address will not be published.