The Principle of Virtual Work: Applications of the Principle of Virtual Work
Learning Outcomes
- Employ the principle of virtual work to calculate the reactions in simple beam systems.
- Identify that the principle of virtual work is equivalent to static equilibrium.
- Employ the principle of virtual work to calculate an approximate solution for a beam system.
- Differentiate between the requirement for an approximate solution and an exact solution.
In this section, we will present three applications for the principle of virtual work. The first applications is for illustrative purposes only to show that the principle of virtual work is equivalent to the equilibrium equations. The second application was widely used to calculate deflections for statically determinate structures. It was also widely used in the past to calculate the reactions for statically indeterminate structures. However, the wide use of the computer programs to calculate the reactions and deflections have rendered the second application almost obsolete. The third application is for finding approximate solutions for continuum mechanics problems. In particular, the majority of the finite element analysis procedure for solving continuum mechanics problems are based on the principle of virtual work.
Application 1: Finding the Reactions of Statically Determinate Beams
Theory
A statically determinate beam is a beam whose external reactions can be obtained by solving the equilibrium equations without the need for using the constitutive equations. In case of a plane beam, the equilibrium equations: the sums of the horizontal and vertical forces, separately, are equal to zero, and the sum of moments is equal to zero. For such beams, it will be shown that the principle of virtual work can be used to generate the same equations by simply applying a virtual displacement field that produces no internal forces. Such a displacement field that produces no internal forces is termed: “Rigid Body Displacement.” Recalling the principle of virtual work derived above for the Euler Bernoulli beams, if the arbitrary smooth displacement field 
is such that:
![\[ \frac{\mathrm{d}^2y^*}{\mathrm{d}X_1^2}=0 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3c56076782c2671717bbdf307b77f40d_l3.png "Rendered by QuickLaTeX.com")
then the internal work done is equal to zero and the statement of the principle of virtual work is reduced to: From an equilibrium position, the work done by the external forces through an arbitrary and smooth displacement field is equal to zero:
![\[ 0= \int_0^L \! qy^* \,\mathrm{d}X_1-V_2y_2^*+V_1y_1^*+M_2\theta_2^*-M_1*\theta_1^* \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c929c61d3e561a2ca0132202f7c1d12e_l3.png "Rendered by QuickLaTeX.com")
See the examples and problems section for examples on this application.
Video
Application 2: Finding Displacements ot Specific Points for Linear Elastic Small Deformation Beams
Theory
Structural engineers often use the method of virtual work to find the displacement at specific points in statically determinate structures when the bending moment, the shearing force, and the normal force diagrams can be computed for the structure under consideration. In that procedure, the internal forces diagram for the structure is solved for twice, once with the original set of external forces and once with a unit load applied at the point of interest. Then, the displacement field from the original set of external forces is considered to be analogous to the virtual displacement field 
in the derivation of the equations of the Virtual Work principle for the Euler Bernoulli beam. The displacement field obtained for the structure with the applied unit load is considered to be analogous to the displacement field 
. Because satisfies the boundary conditions of the structure, the work done by the reactions is equal to zero and therefore, the equation of the principle of virtual work then becomes:
![\[ \int \! EI\frac{\mathrm{d}^2y}{\mathrm{d}X_1^2}\frac{\mathrm{d}^2y^*}{\mathrm{d}X_1^2}\,\mathrm{d}X_1=1\times \Delta^* \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3d4b3c0f82ceedff9e1cebd659d8d64a_l3.png "Rendered by QuickLaTeX.com")
where:
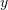- is the displacement field obtained through applying a unit load to the point of interest.
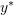- is the displacement field obtained for the structure with the applied loading.
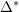is the unknown displacement at the point of interest.
However, since the bending moment diagrams for both the structure with the applied loading and the structure with a unit load applied at the point of interest, the equation can now be rewritten as follows:
![\[ \int \! \frac{M_0m_1}{EI}\,\mathrm{d}X_1=1\times \Delta^* \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a9e9d7a1b34040eaf147a6c5f1c93de6_l3.png "Rendered by QuickLaTeX.com")
If the shear and normal forces deformations are to be considered as well, the equation becomes:
![\[ \int \! \frac{M_0m_1}{EI}\,\mathrm{d}X_1+\int \! \frac{N_0n_1}{EA}\,\mathrm{d}X_1+\int \! \frac{V_0v_1}{kGA}\,\mathrm{d}X_1=1\times \Delta^* \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e4e6779edb2dd5e1b2ae3fc21dc30a62_l3.png "Rendered by QuickLaTeX.com")
where:
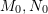, and 
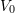are the bending moment, normal force and shearing force equations for the structure with the original set of forces applied to it.
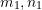, and 
are the bending moment, normal force and shearing force equations for the structure with the unit load applied to the point of interest.
, 
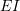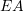, and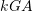 
are the bending, normal force, and shearing force stiffness for the individual beam members.
See the examples below for an example on this application.
Application 3: Finding Approximate Solutions
Theory
The principle of virtual work is applied by first approximating the unknown displacement field of the structure with a shape or a form with a finite number of unknown parameters. The approximate displacement field has to satisfy the boundary conditions of the structure so that the external reactions would not appear in the equations of the principle of the virtual work. Then, the virtual displacement field is applied by varying the unknown parameters. This method results in a finite number of equations that are sufficient to find the unknown parameters. In essence the possible displacement fields of the structure are restricted to a family of displacement functions that have a finite number of unknowns. See the examples and problems section for an example on this application.