Hyperelastic Materials: Videos, Examples, and Problems
Hyperelastic Materials Video
Examples
Example 1
Assume that a unit length cube of material deforms such that the length of the sides parallel to ![]() and
and ![]() become 0.8, 0.625 and l units, respectively, without any rotations. If the material follows a Neo-Hookean material model with
become 0.8, 0.625 and l units, respectively, without any rotations. If the material follows a Neo-Hookean material model with ![]() units, find
units, find ![]() , the Cauchy stress tensor
, the Cauchy stress tensor ![]() and the first Piola Kirchhoff stress tensor
and the first Piola Kirchhoff stress tensor ![]() after deformation in terms of the unknown hydrostatic pressure
after deformation in terms of the unknown hydrostatic pressure ![]() .
.
SOLUTION
The deformation gradient of the above deformation is:
![Rendered by QuickLaTeX.com \[ F=\left(\begin{array}{ccc} 0.8 & 0 & 0\\ 0 & 0.625 & 0\\ 0 & 0 & l \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b926aea52ca28c2aed1c6547f74c6763_l3.png)
The material is incompressible, therefore ![]() units. The first invariant of
units. The first invariant of ![]() is given by:
is given by:
![]()
The strain energy per unit volume of the undeformed configuration is:
![]()
Since ![]() .
.
The stress matrices can be obtained by direct substitution in the equations for the stress:
![Rendered by QuickLaTeX.com \[ P=4\mu F+JpF^{-T}= \left(\begin{array}{ccc} 3.2+1.25p & 0 & 0\\ 0 & 2.5+1.6p & 0\\ 0 & 0 & 8+\frac{p}{2} \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-772fe1adaf513a70333e28f1b72502ff_l3.png)
![Rendered by QuickLaTeX.com \[ \sigma=4\mu FF^T+pI= \left(\begin{array}{ccc} 2.56+p & 0 & 0\\ 0 & 1.5625+p & 0\\ 0 & 0 & 16+p \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-711ddb1ce411dda03c12e9fb91ab71aa_l3.png)
View Mathematica Code
J=Det[F];
mu=1;
I1=Sum[(Transpose[F].F)[[i,i]],{i,1,3}];
P=4*mu*F+J*p*Transpose[Inverse[F]];
sigma=4*mu*F.Transpose[F]+p*IdentityMatrix[3];
P//MatrixForm
sigma//MatrixForm
View Python Code
import sympy as sp
from sympy import *
F = Matrix([[0.8, 0, 0],[0, 0.625, 0],[0,0,2]])
J = det(F)
mu = 1
p = sp.symbols("p")
display("J = det(F) =",J)
display("F =",F)
I = sum(F*F.T)
display("I = sum(FF^T)",I)
P = 4*mu*F+J*p*F.inv().T
display("P = 4\u03BCF + JpF^(-T) =",P)
s = 4*mu*F*F.T+p*eye(3)
display("\u03C3 = 4\u03BCFFF^T+pI =",s)
Example 2
Assume that a unit length cube of material deforms such that the deformation gradient is:
![Rendered by QuickLaTeX.com \[ F=\left(\begin{array}{ccc} \frac{1}{4} & -\frac{1}{2\sqrt{2}} & \frac{1}{4}\\ \frac{1}{4} & \frac{1}{2\sqrt{2}} & \frac{1}{4}\\ -2\sqrt{2} & 0 & 2\sqrt{2} \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-448086c05f2bfdd90dbf036b12b200f0_l3.png)
If the material follows a Neo-Hookean material model with ![]() units, find
units, find ![]() , the Cauchy stress tensor
, the Cauchy stress tensor ![]() and the first Piola Kirchhoff stress tensor
and the first Piola Kirchhoff stress tensor ![]() after deformation in terms of the unknown hydrostatic pressure
after deformation in terms of the unknown hydrostatic pressure ![]() .
.
SOLUTION
The determinant of ![]() is equal to 1, therefore, the deformation is isochoric.
is equal to 1, therefore, the deformation is isochoric.
![]()
Both values of the strain energy per unit volume in the undeformed and the deformed configurations are equal:
![]()
The stress matrices can be obtained by direct substitution in the equations for the stress:
![Rendered by QuickLaTeX.com \[ P=4\mu F+JpF^{-T}= \left(\begin{array}{ccc} 1+p & -\sqrt{2}(1+p) & 1+p\\ 1+p & \sqrt{2}(1+p) & 1+p\\ -8\sqrt{2}-\frac{p}{4\sqrt{2}} & 0 & 8\sqrt{2}+\frac{p}{4\sqrt{2}} \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-5ee6a0cb19d31c4e3d0e66c112630c68_l3.png)
![Rendered by QuickLaTeX.com \[ \sigma=4\mu FF^T+pI= \left(\begin{array}{ccc} 1+p & 0 & 0\\ 0 & 1+p & 0\\ 0 & 0 & 64+p \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f4b66a66dda828811c31630f852d28a7_l3.png)
View Mathematica Code
F = {{1/4, -1/2/Sqrt[2], 1/4}, {1/4, 1/2/Sqrt[2], 1/4}, {-2*Sqrt[2],
0, 2 Sqrt[2]}}
J = Det[F]
mu = 1
I1 = Sum[(Transpose[F] . F)[[i, i]], {i, 1, 3}]
P = 4*mu*F + J*p*Transpose[Inverse[F]];
sigma = 4*mu*F . Transpose[F] + p*IdentityMatrix[3];
P // MatrixForm
sigma // MatrixForm
View Python Code
import sympy as sp
from sympy import *
F = Matrix([[1/4,-1/(2*sp.sqrt(2)),1/4],
[1/4,1/(2*sp.sqrt(2)),1/4],
[-2*sp.sqrt(2),0,2*sp.sqrt(2)]])
J = det(F)
mu = 1
p = sp.symbols("p")
display("J = det(F) =",J)
display("F =",F)
I = sum(F*F.T)
display("I = sum(FF^T)",I)
P = 4*mu*F+J*p*F.inv().T
display("P = 4\u03BCF + JpF^(-T) =",P)
s = 4*mu*F*F.T+p*eye(3)
display("\u03C3 = 4\u03BCFFF^T+pI =",s)
Example 3
Draw the relationships between the components ![]() and
and ![]() of the first Piola Kirchhoff stress tensor and the Cauchy stress tensor, respectively, versus
of the first Piola Kirchhoff stress tensor and the Cauchy stress tensor, respectively, versus ![]() in a uniaxial state of stress using the three material models (Linear Elastic, Compressible Neo-Hookean, and compressible Mooney-Rivlin material (assuming
in a uniaxial state of stress using the three material models (Linear Elastic, Compressible Neo-Hookean, and compressible Mooney-Rivlin material (assuming ![]() )). Assume that the material is isotropic and no rotations occur during deformation. Assume two cases such that in the first case, in small deformations, the equivalent Young’s modulus and Poisson’s ratio are
)). Assume that the material is isotropic and no rotations occur during deformation. Assume two cases such that in the first case, in small deformations, the equivalent Young’s modulus and Poisson’s ratio are ![]() and
and ![]() respectively. In the second case, in small deformations, the equivalent Young’s modulus and Poisson’s ratio are
respectively. In the second case, in small deformations, the equivalent Young’s modulus and Poisson’s ratio are ![]() and
and ![]() respectively.
respectively.
SOLUTION
Because of the isotropy of the material, we can assume the following form for ![]() :
:
![Rendered by QuickLaTeX.com \[F= \left(\begin{array}{ccc} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_2 \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-98ad91b4e7bebbe449719f89c64adddc_l3.png)
therefore ![]() and
and
![Rendered by QuickLaTeX.com \[F^{-T}= \left(\begin{array}{ccc} \frac{1}{\lambda_1} & 0 & 0\\ 0 & \frac{1}{\lambda_2} & 0\\ 0 & 0 & \frac{1}{\lambda_2} \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7d37a5f34f0612cbeec2d36dca95e4fd_l3.png)
Linear Elastic Material:
For a linear elastic isotropic material,
![Rendered by QuickLaTeX.com \[ \varepsilon= \left(\begin{array}{ccc} \lambda_1-1 & 0 & 0\\ 0 & \lambda_2-1 & 0\\ 0 & 0 & \lambda_2-1 \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-20858d626b5325989531b713a446e947_l3.png)
and therefore:
![Rendered by QuickLaTeX.com \[ \sigma=\frac{E}{(1-2\nu)(1+\nu)} \left(\begin{array}{ccc} \lambda_1(1-\nu)+2\nu\lambda_2-(1+\nu) & 0 & 0\\ 0 & \lambda_2+\nu\lambda_1-(1+\nu) & 0\\ 0 & 0 & \lambda_2+\nu\lambda_1-(1+\nu) \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-95f794668b8a714e858608f1a245c33d_l3.png)
Since it is a uniaxial state of stress, we have ![]() , therefore,
, therefore, ![]()
Then:
![Rendered by QuickLaTeX.com \[ \sigma=E \left(\begin{array}{ccc} \lambda_1-1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3faa23b46c260520172d241159b2ebe1_l3.png)
The first Piola Kirchhoff stress is:
![Rendered by QuickLaTeX.com \[ P=J\sigma F^{-T}=E(-\nu\lambda_1+1+\nu)^2 \left(\begin{array}{ccc} \lambda_1-1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-69fd045c5d5f1a5f4b064290508ad502_l3.png)
Therefore, ![]()
Compressible Neo-Hookean Material:
The strain energy function, the first Piola Kirchhoff stress tensor and the Cauchy stress tensor are given by:
![]()
![]()
![]()
Where ![]() and
and ![]() are material constants that can be calibrated as described above such that
are material constants that can be calibrated as described above such that ![]() and
and ![]()
The normal components of the Cauchy stress in the second and third directions are given by:
![]()
Setting ![]() we get a relationship between
we get a relationship between ![]() and
and ![]() which can be used to substitute for
which can be used to substitute for ![]() . The equations can be solved numerically by first assuming a value for
. The equations can be solved numerically by first assuming a value for ![]() , then solving for
, then solving for ![]() and substituting in the expressions for
and substituting in the expressions for ![]() and
and ![]() .
.
For a Compressible Mooney-Rivlin Material:
The strain energy function, the first Piola Kirchhoff stress tensor and the Cauchy stress tensor are given by:
![]()
![]()
![]()
Where ![]() and
and ![]() are material constants and can be calibrated as shown above such that
are material constants and can be calibrated as shown above such that ![]() and
and ![]()
In the above relationship we have ![]() . Setting
. Setting ![]() we get a relationship between
we get a relationship between ![]() and
and ![]() which can be used to substitute for
which can be used to substitute for ![]() . The equations can be solved numerically by first assuming a value for
. The equations can be solved numerically by first assuming a value for ![]() , then solving for
, then solving for ![]() and substituting in the expressions for
and substituting in the expressions for ![]() and
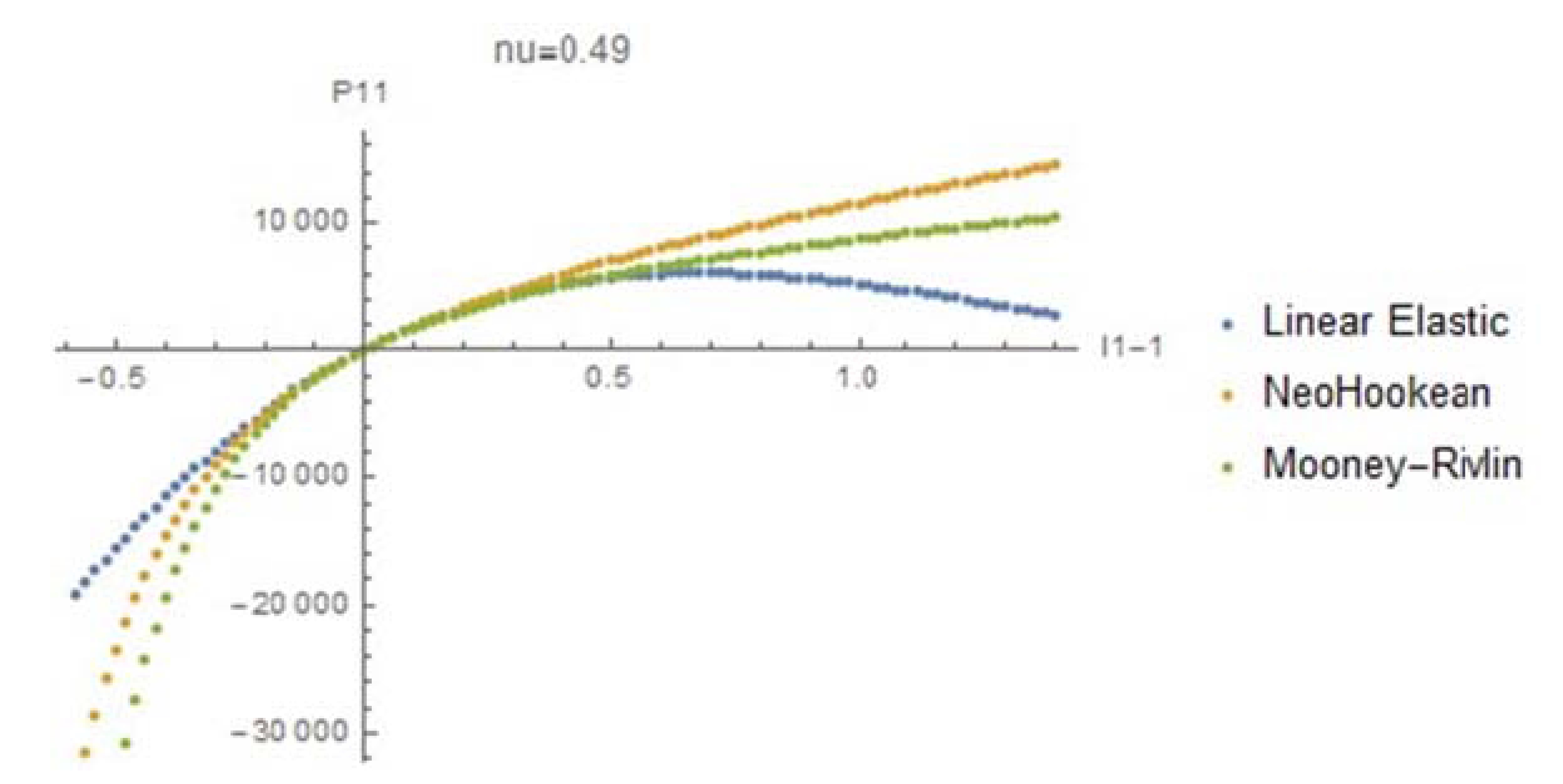
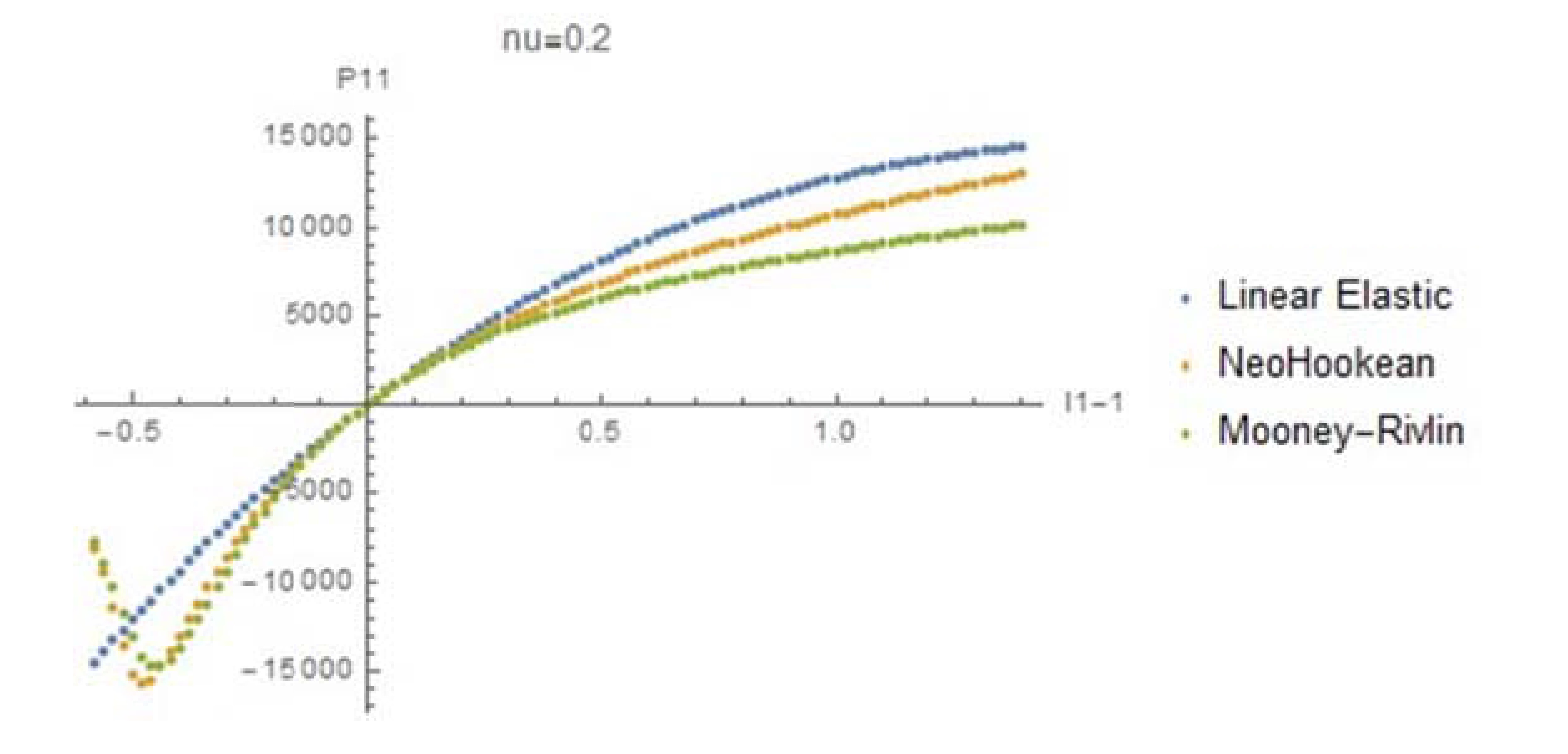
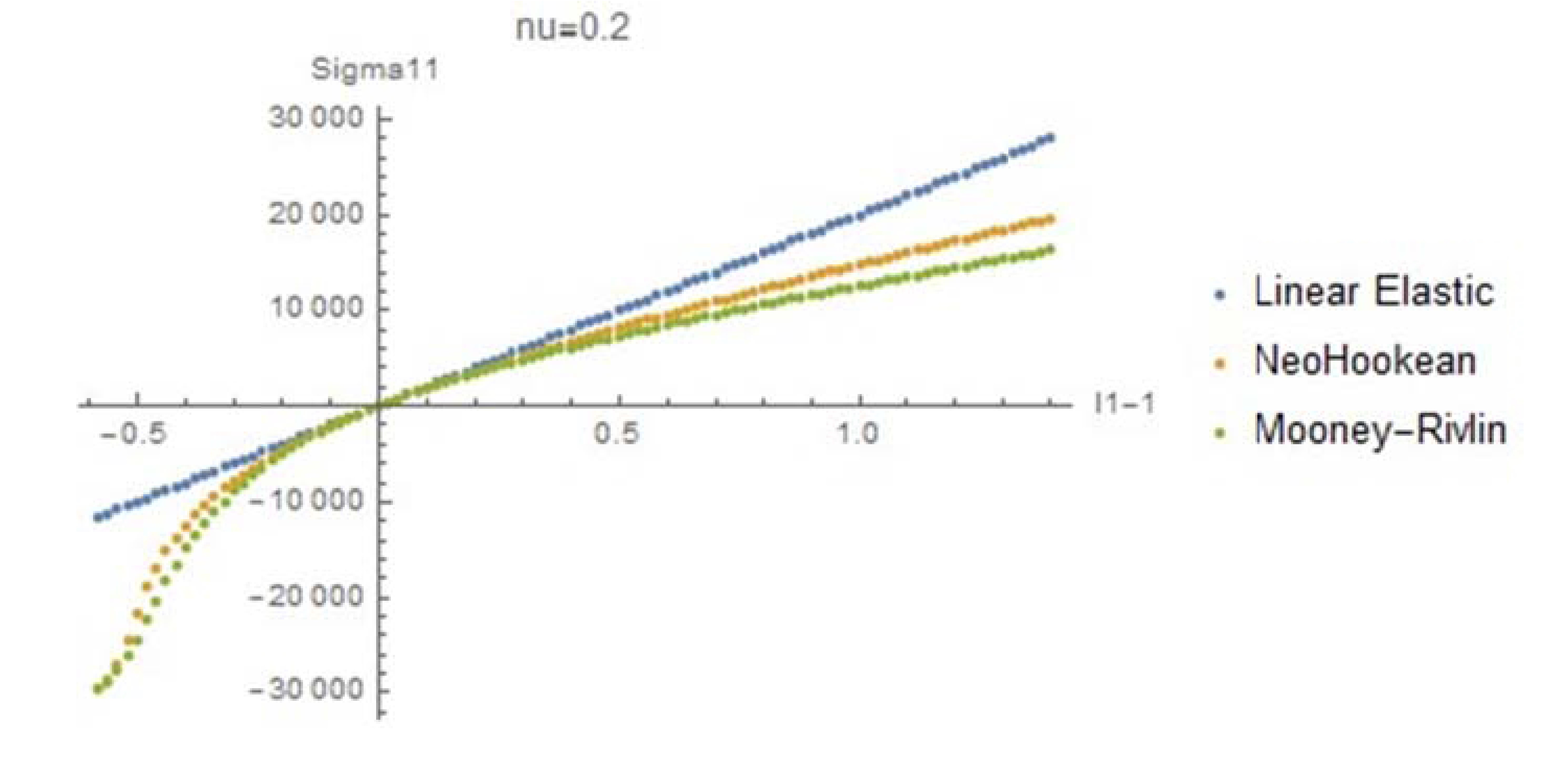
and ![]() . The required plots are shown below with MPa units for the stresses. Note the following, for
. The required plots are shown below with MPa units for the stresses. Note the following, for ![]() , the first Piola Kirchhoff stress tensor component
, the first Piola Kirchhoff stress tensor component ![]() starts decreasing after
starts decreasing after ![]() reaches around 0.5. This is because of the high Poisson’s ratio. In other words, the applied force on the material decreases because of the high incompressibility and the decrease in the width! For
reaches around 0.5. This is because of the high Poisson’s ratio. In other words, the applied force on the material decreases because of the high incompressibility and the decrease in the width! For ![]() , this behaviour is not observed, but for large compressive strain, the material behaviour is not ideal; The applied load decreases with increased compressive strain. These plots show that if such materials are to be used, care has to be taken to carefully select the required model and the corresponding material parameters.
, this behaviour is not observed, but for large compressive strain, the material behaviour is not ideal; The applied load decreases with increased compressive strain. These plots show that if such materials are to be used, care has to be taken to carefully select the required model and the corresponding material parameters.

View Mathematica Code
(*For nu=0.2*)
Clear[l1, l2, s11, s22, Ee, nu]
F = {{l1, 0, 0}, {0, l2, 0}, {0, 0, l2}};
F // MatrixForm
Fnt = Transpose[Inverse[F]];
Fnt // MatrixForm
J = Det[F];
U2 = Transpose[F] . F;
U4 = U2 . U2;
I1 = Sum[U2[[i, i]], {i, 1, 3}];
I2 = 1/2*(I1^2 - Sum[U4[[i, i]], {i, 1, 3}]);
(*Linear Elastic Material*)
eps11 = l1 - 1;
eps22 = l2 - 1;
eps33 = l2 - 1;
s11 = Ee/(1 - 2 nu)/(1 + nu)*(eps11*(1 - nu) + eps22*nu + eps33*nu);
s22 = Ee/(1 - 2 nu)/(1 + nu)*(eps22*(1 - nu) + eps11*nu + eps33*nu);
a1 = FullSimplify[Solve[s22 == 0, l2]]
sigma = FullSimplify[{{s11, 0, 0}, {0, s22, 0}, {0, 0, s22}} /.
a1[[1]]];
sigma // MatrixForm
P = FullSimplify[J*sigma*Fnt /. a1[[1]]];
P // MatrixForm
RelC1 = Table[{0.4 + i/50 - 1,
sigma[[1, 1]] /. {l1 -> 0.4 + i/50}}, {i, 1, 100}];
RelP1 = Table[{0.4 + i/50 - 1, P[[1, 1]] /. {l1 -> 0.4 + i/50}}, {i,
1, 100}];
(*Compressible Neo-Hookean material*)
Ee = 20000;
nu = 0.2;
G = Ee/2/(1 + nu);
Kk = Ee/3/(1 - 2 nu);
C10 = G/2
Dd = 2/Kk
sigmaNH =
FullSimplify[
C10*J^(-5/3)*(2 F . Transpose[F] - 2 I1/3*IdentityMatrix[3]) +
2/Dd*(J - 1) IdentityMatrix[3]];
sigmaNH // MatrixForm
PiolaNH = FullSimplify[J*sigmaNH . Fnt];
PiolaNH // MatrixForm
lambda = Table[0, {i, 150}];
CauchyS11 = Table[0, {i, 100}];
Piola11 = Table[0, {i, 100}];
Do[lambda[[i]] = 0.4 + i/50;
s = l1 -> lambda[[i]];
s2 = FindRoot[(sigmaNH[[2, 2]] /. s) == 0, {l2, 2}];
CauchyS11[[i]] = (sigmaNH[[1, 1]] /. s2) /. s;
Piola11[[i]] = (PiolaNH[[1, 1]] /. s2) /. s, {i, 1, 100}];
RelC2 = Table[{lambda[[i]] - 1, CauchyS11[[i]]}, {i, 1, 100}];
RelP2 = Table[{lambda[[i]] - 1, Piola11[[i]]}, {i, 1, 100}];
(*Compressible Mooney-Rivlin material*)
C10 = G/4
C01 = G/4
sigmaMN =
FullSimplify[
C10*J^(-5/3)*(2 F . Transpose[F] - 2 I1/3*IdentityMatrix[3]) +
C01*J^(-7/3) (2 I1*F . Transpose[F] -
2 F . Transpose[F] . F . Transpose[F] -
4 I2/3*IdentityMatrix[3]) + 2/Dd*(J - 1) IdentityMatrix[3]];
sigmaMN // MatrixForm
PiolaMN = FullSimplify[J*sigmaMN . Fnt];
PiolaMN // MatrixForm
Do[lambda[[i]] = 0.4 + i/50;
s = l1 -> lambda[[i]];
s2 = FindRoot[(sigmaMN[[2, 2]] /. s) == 0, {l2, 2}];
CauchyS11[[i]] = (sigmaMN[[1, 1]] /. s2) /. s;
Piola11[[i]] = (PiolaMN[[1, 1]] /. s2) /. s, {i, 1, 100}];
RelC3 = Table[{lambda[[i]] - 1, CauchyS11[[i]]}, {i, 1, 100}];
RelP3 = Table[{lambda[[i]] - 1, Piola11[[i]]}, {i, 1, 100}];
ListPlot[{RelP1, RelP2, RelP3}, AxesLabel -> {"l1-1", "P11"},
PlotLabel -> "nu=0.2",
PlotLegends -> {"Linear Elastic", "NeoHookean",
"Mooney-Rivlin"}] ListPlot[{RelC1, RelC2, RelC3},
AxesLabel -> {"l1-1", "Sigma11"}, PlotLabel -> "nu=0.2",
PlotLegends -> {"Linear Elastic", "NeoHookean", "Mooney-Rivlin"}]
View Python Code
import sympy as sp
from sympy import *
l1,l2,Ee,nu = sp.symbols("lambda_1 lambda_2 epsilon nu")
from matplotlib import pyplot as plt
from scipy.optimize import root
# plot
x = [0]*100
RelC1 = [0]*100
RelP1 = [0]*100
RelC2 = [0]*100
RelP2 = [0]*100
RelC3 = [0]*100
RelP3 = [0]*100
for i in range(100):
x[i] = 0.4 + (i+1)/50
F = Matrix([[l1,0,0],[0,l2,0],[0,0,l2]])
display("F =",F)
Fnt = F.inv().T
display("F^(-T) =",Fnt)
J = det(F)
U2 = F.T*F
U4 = U2*U2
I1 = sum(U2)
I2 = 1/2*(I1**2 - sum(U4))
def plot(Nu):
display("Set Nu =",Nu)
# linear elastic material
E = F -eye(3)
display("Linear Elastic Material")
display("\u03B5 =", E)
E11, E22, E33 = E[0,0], E[1,1], E[2,2]
s11 = Ee/(1-2*nu)/(1+nu)*(E11*(1-nu)+E22*nu+E33*nu)
s22 = Ee/(1-2*nu)/(1+nu)*(E22*(1-nu)+E11*nu+E33*nu)
display("For \u03C3_22 = 0: ",Eq(s22,0))
a1 = solve(s22, [l2])[0]
display("\u03BB2 =", a1)
sigma = Matrix([[s11,0,0],[0,s22,0],[0,0,s22]])
sigma = simplify(sigma.subs({l2:a1}))
P = (J*sigma*Fnt).subs({l2:a1})
display("\u03C3 =",sigma)
display("P =",P)
sigma = sigma.subs({Ee:20000, nu:Nu})
P = P.subs({Ee:20000, nu:0.2})
for i in range(100):
RelC1[i] = sigma[0,0].subs({l1:x[i]})
RelP1[i] = P[0,0].subs({l1:x[i]})
# Compressible Neo-Hookean materials
display("Compressible Neo-Hookean materials")
G = Ee/2/(1+nu)
G = G.subs({nu:Nu,Ee:20000})
Kk = Ee/3/(1-2*nu)
Kk = Kk.subs({nu:Nu,Ee:20000})
C10 = G/2
display("C10 =",C10)
Dd = 2/Kk
display("Dd =",Dd)
sigmaNH = simplify(C10*J**(-5/3)*(2*F*F.T-2*I1/3*eye(3))
+2/Dd*(J-1)*eye(3))
PiolaNH = simplify(J*sigmaNH*Fnt)
display("\u03C3 =",sigmaNH)
display("P =",PiolaNH)
SolsigmaNH = sigmaNH[1,1].subs({l1:x[0]})
for i in range(100):
SolsigmaNH = sigmaNH[1,1].subs({l1:x[i]})
SolsigmaNH = lambdify(l2,SolsigmaNH)
sol = root(SolsigmaNH,[2])
RelC2[i] = sigmaNH[0,0].subs({l1:x[i], l2:sol.x[0]})
RelP2[i] = PiolaNH[0,0].subs({l1:x[i], l2:sol.x[0]})
# Compressible Mooney-Rivlin materials
display("Compressible Mooney-Rivlin materials")
C10 = G/4
C01 = G/4
display("C10 =",C10)
display("C01 =",C01)
sigmaMN = simplify(C10*J**(-5/3)*(2*F*F.T-2*I1/3*eye(3))
+C01*J**(-7/3)*(2*I1*F*F.T-2*F*F.T*F*F.T-4*I2/3*eye(3))
+2/Dd*(J-1)*eye(3))
PiolaMN = simplify(J*sigmaMN*Fnt)
display("\u03C3 =",sigmaMN)
display("P =",PiolaMN)
for i in range(100):
SolsigmaNH = sigmaNH[1,1].subs({l1:x[i]})
SolsigmaNH = lambdify(l2,SolsigmaNH)
sol = root(SolsigmaNH,[2])
RelC3[i] = sigmaMN[0,0].subs({l1:x[i], l2:sol.x[0]})
RelP3[i] = PiolaMN[0,0].subs({l1:x[i], l2:sol.x[0]})
# plots
xL = [i -1 for i in x]
fig, ax = plt.subplots()
title = "\u03BC = " + str(Nu)
plt.title(title)
plt.xlabel("\u03BB - 1")
plt.ylabel("P11")
ax.scatter(xL, RelP1, label="Linear Elastic", s=1)
ax.scatter(xL, RelP2, label="NeoHookean",s=1)
ax.scatter(xL, RelP3, label="Mooney-Rivlin ",s=1)
ax.legend()
ax.grid(True, which='both')
ax.axhline(y = 0, color = 'k')
ax.axvline(x = 0, color = 'k')
fig, ax = plt.subplots()
plt.title(title)
plt.xlabel("\u03BB - 1")
plt.ylabel("Sigma11")
ax.scatter(xL, RelC1, label="Linear Elastic",s=1)
ax.scatter(xL, RelC2, label="NeoHookean",s=1)
ax.scatter(xL, RelC3, label="Mooney-Rivlin",s=1)
ax.legend()
ax.grid(True, which='both')
ax.axhline(y = 0, color = 'k')
ax.axvline(x = 0, color = 'k')
plot(0.49)
plot(0.2)
Problems
- It was shown above that for an isotropic hyperelastic material, the eigenvectors of the Cauchy stress tensor are aligned with the eigenvectors of
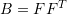 . Show that this implies that the eigenvectors of the second Piola Kirchhoff stress are aligned with the eigenvectors of
. Show that this implies that the eigenvectors of the second Piola Kirchhoff stress are aligned with the eigenvectors of  . (Hint: You need to first show that the eigenvectors of
. (Hint: You need to first show that the eigenvectors of  and
and 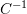 are aligned).
are aligned). - Show the following relationships:
![Rendered by QuickLaTeX.com \[ \frac{\partial C_{ij}}{\partial F_{ab}}=F_{aj}\delta_{bi}+F_{ai}\delta_{bj} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-481e3dbfdf50c8ffebec7ab7e9059c97_l3.png)
![Rendered by QuickLaTeX.com \[ \frac{\partial W}{\partial F}=2F\frac{\partial W}{\partial C} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9e40be6d7b74ed3fb0ea8b2c8fb31495_l3.png)
- Utilize the previous exercise to show that if
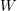 is the strain energy function of an elastic material, then, the second Piola-Kirchhoff stress tensor is obtained as:
is the strain energy function of an elastic material, then, the second Piola-Kirchhoff stress tensor is obtained as:
![Rendered by QuickLaTeX.com \[ S=\frac{\partial W}{\partial \varepsilon_{Green}}=2\frac{\partial W}{\partial C} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b96575e2495d8d4c0031906a4fe085f3_l3.png)
- Consider the polar decomposition
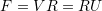 . Find an expression for the components of
. Find an expression for the components of 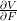 and
and 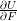 . If W is the strain energy density per unit volume in the undeformed configuration. Show the following:
. If W is the strain energy density per unit volume in the undeformed configuration. Show the following:
![Rendered by QuickLaTeX.com \[ \frac{\partial W}{\partial F}=\frac{\partial W}{\partial V}R=R\frac{\partial W}{\partial U} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-132df006431b28de5c7a6e8caf382b60_l3.png)
- The following anisotropic hyperelastic model was developed by Epstein and Elzanowski.
where![Rendered by QuickLaTeX.com \[ W=\frac{\mu}{2}\left(I_1(\tilde{C})-3 -2\ln\left(\sqrt{\det(\tilde{C})}\right)\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-26fd602454f1d39d419bc930a747ba5f_l3.png)
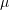 is a material constant,
is a material constant, 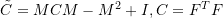 , and
, and 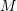 is a positive definite symmetric matrix. Show that the Cauchy stress matrix for this material is given by:
is a positive definite symmetric matrix. Show that the Cauchy stress matrix for this material is given by:
![Rendered by QuickLaTeX.com \[ \sigma=\frac{\mu}{J}\left(FM^2F^T-FM\tilde{C}^{-1}MF^T\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9d0bcf3705f5088c8b8080005f30d17d_l3.png)
- Assume that a material that follows the incompressible Neo-Hookean hyperelastic material model exhibits the following two different cases of deformation:
- Simple shear deformation
- Biaxial extension with stretches of
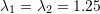 with no rotations
with no rotations
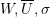 and
and  in terms of the undetermined hydrostatic stress
in terms of the undetermined hydrostatic stress 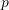 for each case.
for each case.
- Assume that a compressible isotropic hyperelastic material exhibits the following two different cases of deformation:
- Simple shear deformation
- Biaxial extension with stretches of
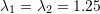 and
and 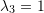 with no rotations
with no rotations
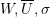 and
and  for each of the above cases of deformation and for each of the following material models:
for each of the above cases of deformation and for each of the following material models:
- Neo-Hookean material model
- Mooney-Rivlin material model
- Show that the relationship imposed by the principle of material frame-invariance
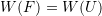 implies the following:
implies the following:
![Rendered by QuickLaTeX.com \[\sigma(F)=R\sigma(U)R^T, P(F)=RP(U) and S(F)=S(U)\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d5256c433bf6c4c477751327a810592e_l3.png)
