Calculus: Vector Calculus
Fields
Let ![]() be a set. Scalar, vector or tensor valued functions defined on
be a set. Scalar, vector or tensor valued functions defined on ![]() are denoted as scalar, vector or tensor fields respectively. If
are denoted as scalar, vector or tensor fields respectively. If ![]() is a subset of
is a subset of ![]() and if
and if ![]() ,
, ![]() , and
, and ![]() are scalar, vector and second-order tensor fields respectively, then by choosing a coordinate system defined by the orthonormal basis set
are scalar, vector and second-order tensor fields respectively, then by choosing a coordinate system defined by the orthonormal basis set ![]() , then the arguments of the functions can be chosen to be the cartesian coordinates
, then the arguments of the functions can be chosen to be the cartesian coordinates ![]() such that
such that ![]() :
:
![]()
FIeld Derivatives
Change of Basis
By the results of the change of basis section, if another orthonormal basis set ![]() is chosen, where
is chosen, where ![]() is the transformation matrix defined as
is the transformation matrix defined as ![]() , then the components in the new orthonormal basis set
, then the components in the new orthonormal basis set ![]() are related to the original components using the relationship:
are related to the original components using the relationship:
![]()
The matrix ![]() is related to the derivatives of the components of
is related to the derivatives of the components of ![]() with respect to the original components
with respect to the original components ![]() as follows:
as follows:
![]()
and since ![]() we also have:
we also have:
![]()
The above relationships will be useful when calculating the derivatives of other fields.
Gradient of a Scalar Field
Let ![]() be a scalar field,
be a scalar field, ![]() is said to be continuous at
is said to be continuous at ![]() if
if
![]()
Alternatively, ![]() is continuous at
is continuous at ![]() if
if ![]() we have:
we have:
![]()
![]() is said to be continuous if it is continuous at every point.
is said to be continuous if it is continuous at every point.
![]() is said to be differentiable if there exists a vector field denoted
is said to be differentiable if there exists a vector field denoted ![]() or
or ![]() such that
such that ![]()
![]()
The gradient vector field ![]() is unique since if another vector field
is unique since if another vector field ![]() satisfies the above equation, we have
satisfies the above equation, we have ![]() :
:
![]()
Since ![]() is arbitrary, we have:
is arbitrary, we have:
![]()
By replacing ![]() with the basis vectors
with the basis vectors ![]() ,
,![]() and
and ![]() , then the components of the vector
, then the components of the vector ![]() have the form:
have the form:
![Rendered by QuickLaTeX.com \[ \nabla\phi = \left(\begin{array}{c} \frac{\partial\phi}{\partial x_1}\\ \frac{\partial\phi}{\partial x_2}\\ \frac{\partial\phi}{\partial x_3} \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-87c7b35df939ed07173ea7f75efec293_l3.png)
The components of the vector ![]() using an orthonormal basis set
using an orthonormal basis set ![]() are related to the components of
are related to the components of ![]() using the relationship:
using the relationship:
![Rendered by QuickLaTeX.com \[\begin{split} (\nabla\phi)' &= \left(\begin{array}{c} \frac{\partial\phi}{\partial x'_1}\\ \frac{\partial\phi}{\partial x'_2}\\ \frac{\partial\phi}{\partial x'_3} \end{array} \right) = \left(\begin{array}{c} \frac{\partial\phi}{\partial x_1}\frac{\partial x_1}{\partial x'_1}+\frac{\partial\phi}{\partial x_2}\frac{\partial x_2}{\partial x'_1}+\frac{\partial\phi}{\partial x_3}\frac{\partial x_3}{\partial x'_1}\\ \frac{\partial\phi}{\partial x_1}\frac{\partial x_1}{\partial x'_2}+\frac{\partial\phi}{\partial x_2}\frac{\partial x_2}{\partial x'_2}+\frac{\partial\phi}{\partial x_3}\frac{\partial x_3}{\partial x'_2}\\ \frac{\partial\phi}{\partial x_1}\frac{\partial x_1}{\partial x'_3}+\frac{\partial\phi}{\partial x_2}\frac{\partial x_2}{\partial x'_3}+\frac{\partial\phi}{\partial x_3}\frac{\partial x_3}{\partial x'_3} \end{array} \right)\\ & = \left(\begin{array}{ccc} \frac{\partial x_1}{\partial x'_1} & \frac{\partial x_2}{\partial x'_1} &\frac{\partial x_3}{\partial x'_1}\\ \frac{\partial x_1}{\partial x'_2} & \frac{\partial x_2}{\partial x'_2} &\frac{\partial x_3}{\partial x'_2}\\ \frac{\partial x_1}{\partial x'_3} & \frac{\partial x_2}{\partial x'_3} &\frac{\partial x_3}{\partial x'_3} \end{array} \right) \left(\begin{array}{c} \frac{\partial \phi}{\partial x_1}\\ \frac{\partial \phi}{\partial x_2}\\ \frac{\partial \phi}{\partial x_3} \end{array} \right)\\ &=Q \nabla\phi \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8f67928d8f45fce1887abe52472cbe00_l3.png)
Therefore, the transformation of the vector ![]() follows the same rule for the change of basis for vectors in the Euclidean vector space
follows the same rule for the change of basis for vectors in the Euclidean vector space ![]() .
.
The directional derivative of the scalar field ![]() in the direction of a fixed unit vector
in the direction of a fixed unit vector ![]() (i.e.,
(i.e., ![]() ) is defined as:
) is defined as:
![]()
The maximum value for the directional derivative is attained when n is chosen in the direction of the vector ![]() . On the other hand, the directional derivative in the direction of any vector that is normal (perpendicular) to
. On the other hand, the directional derivative in the direction of any vector that is normal (perpendicular) to ![]() is obviously zero. In other words, the vector field
is obviously zero. In other words, the vector field ![]() points towards the direction of the maximum change of the scalar field
points towards the direction of the maximum change of the scalar field ![]() .
.
Partial Derivatives and Differentiability
Note that if the partial derivatives of ![]() exist, they do not guarantee that
exist, they do not guarantee that ![]() is differentiable at every point. Consider the following counter example:
is differentiable at every point. Consider the following counter example:
![]()
The function ![]() is continuous at every point including at
is continuous at every point including at ![]() , why?. In addition, the partial derivatives with respect to
, why?. In addition, the partial derivatives with respect to ![]() and
and ![]() are defined as:
are defined as:
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\partial\phi}{\partial x} &= \begin{cases} 0, & \text{if }(x,y)=(0,0)\\ \frac{6xy^3}{(x^2+y^2)^2}, & \text{otherwise} \end{cases}\\ \frac{\partial\phi}{\partial y}&= \begin{cases} 0, & \text{if }(x,y)=(0,0)\\ \frac{3x^2(x^2-y^2)}{(x^2+y^2)^2}, & \text{otherwise} \end{cases} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a5e57e520a585df3fa64f5b95e21f80c_l3.png)
However, ![]() is not differentiable at
is not differentiable at ![]() . Consider the direction
. Consider the direction ![]() , then the directional derivative along
, then the directional derivative along ![]() at the point
at the point ![]() can be evaluated using the dot product:
can be evaluated using the dot product:
![]()
However, the limit along the line ![]() gives a non zero value:
gives a non zero value:
![]()
It is worth noting that the partial derivative ![]() is not continuous at
is not continuous at ![]() . Since
. Since
![]()
while
![]()
therefore, ![]() is not continuous.
is not continuous.
However, there is a theorem from vector calculus that states that ![]() is differentiable if and only if the partial derivatives exist and are continuous. The proof of this theorem can be found in multivariate calculus textbooks.
is differentiable if and only if the partial derivatives exist and are continuous. The proof of this theorem can be found in multivariate calculus textbooks.
Gradient of a Vector Field
Let ![]() be a vector field,
be a vector field, ![]() is said to be continuous at
is said to be continuous at ![]() if
if
![]()
Alternatively, ![]() is continuous at
is continuous at ![]() if
if ![]() we have:
we have:
![]()
Alternatively, ![]() is continuous at
is continuous at ![]() if every component
if every component ![]() of the vector field
of the vector field ![]() is a continuous scalar function.
is a continuous scalar function.
![]() is said to be continuous if it is continuous at every point.
is said to be continuous if it is continuous at every point.
![]() is said to be differentiable if there exists a tensor field denoted
is said to be differentiable if there exists a tensor field denoted ![]() or
or ![]() such that
such that ![]() ,
, ![]()
![]()
The gradient tensor field ![]() is unique since if another tensor field
is unique since if another tensor field ![]() satisfies the above equation, we have
satisfies the above equation, we have ![]() :
:
![]()
Since ![]() is arbitrary, we have:
is arbitrary, we have:
![]()
By replacing ![]() with the basis vectors
with the basis vectors ![]() and
and ![]() , then the components of the tensor
, then the components of the tensor ![]() have the form:
have the form:
![Rendered by QuickLaTeX.com \[ \nabla u = \left(\begin{array}{ccc} \frac{\partial u_1}{\partial x_1}& \frac{\partial u_1}{\partial x_2}&\frac{\partial u_1}{\partial x_3}\\ \frac{\partial u_2}{\partial x_1}& \frac{\partial u_2}{\partial x_2}&\frac{\partial u_2}{\partial x_3}\\ \frac{\partial u_3}{\partial x_1}& \frac{\partial u_3}{\partial x_2}&\frac{\partial u_3}{\partial x_3} \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-02bc22d332fa291dae9a204b0d96ca55_l3.png)
The components of the tensor ![]() using an orthonormal basis set
using an orthonormal basis set ![]() are related to the components of
are related to the components of ![]() using the relationship:
using the relationship:
![]()
Therefore,
![]()
I.e.,the transformation of the tensor ![]() follows the same rule for the change of basis for tensors in the Euclidean vector space
follows the same rule for the change of basis for tensors in the Euclidean vector space ![]() .
.
Similar to the scalar fields, the existence of the partial derivatives of a vector field does not guarantee the differentiability except when the partial derivatives are continuous.
Divergence of a Vector Field
Let ![]() be a differentiable vector field, then, the divergence of
be a differentiable vector field, then, the divergence of ![]() denoted by
denoted by ![]() is a scalar field defined as:
is a scalar field defined as:
![]()
Using the properties of the trace function, the divergence operator can be written in terms of the components of ![]() as follows:
as follows:
![]()
Gradient of a Tensor Field
In order to assess continuity and differentiability of tensors, we first have to define what we mean by the size or norm of a tensor. If ![]() , then we can define the following norm function on such tensors as follows:
, then we can define the following norm function on such tensors as follows:
![]()
In other words, the norm of ![]() , is the supremum of the norms of the vectors
, is the supremum of the norms of the vectors ![]() where
where ![]() is a unit vector and
is a unit vector and ![]() . One should check that this definition satisfies the required properties of a norm function as shown in the definitions of linear vector spaces.
. One should check that this definition satisfies the required properties of a norm function as shown in the definitions of linear vector spaces.
Let ![]() be a tensor field,
be a tensor field, ![]() is said to be continuous at
is said to be continuous at ![]() if
if
![]()
Alternatively, ![]() is continuous at
is continuous at ![]() if
if ![]() we have:
we have:
![]()
Alternatively, ![]() is continuous at
is continuous at ![]() if every component
if every component ![]() of the tensor field
of the tensor field ![]() is a continuous scalar function.
is a continuous scalar function.
![]() is said to be continuous if it is continuous at every point.
is said to be continuous if it is continuous at every point.
![]() is said to be differentiable if there exists a third-order tensor field denoted
is said to be differentiable if there exists a third-order tensor field denoted ![]() or
or ![]() such that
such that ![]() ,
, ![]()
![]()
The gradient third-order tensor field ![]() is unique since if another tensor field
is unique since if another tensor field ![]() satisfies the above equation, we have
satisfies the above equation, we have ![]() :
:
![]()
Since ![]() is arbitrary, we have:
is arbitrary, we have:
![]()
By replacing ![]() with the basis vectors
with the basis vectors ![]() and
and ![]() , then the components of the tensor
, then the components of the tensor ![]() have the form:
have the form:
![]()
The components of the tensor ![]() using an orthonormal basis set
using an orthonormal basis set ![]() are related to the components of
are related to the components of ![]() using the relationship:
using the relationship:
![Rendered by QuickLaTeX.com \[ (\nabla T)'_{ijk}=\frac{\partial T'_{ij}}{\partial x'_k}=\sum_{l,m,n=1}^3\frac{\partial Q_{il}T_{lm}Q_{jm}}{\partial x_n}\frac{\partial x_n}{\partial x'_k}=\sum_{l,m,n=1}^3 Q_{il}Q_{jm}Q_{kn}\frac{\partial T_{lm}}{\partial x_n} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cb9ecda31acf3b11b4d5a2f8ff0d591f_l3.png)
I.e.,the transformation of the tensor ![]() follows the same rule for the change of basis for second-order tensors in the Euclidean vector space
follows the same rule for the change of basis for second-order tensors in the Euclidean vector space ![]() .
.
Similar to the scalar fields, the existence of the partial derivatives of a vector field does not guarantee the differentiability except when the partial derivatives are continuous.
DIvergence of a Tensor Field
Let ![]() be a differentiable vector field, then, the divergence of
be a differentiable vector field, then, the divergence of ![]() denoted by
denoted by ![]() is a vector field defined such that
is a vector field defined such that ![]() :
:
![]()
By replacing ![]() with the basis vectors
with the basis vectors ![]() and
and ![]() , then the components of the vector
, then the components of the vector ![]() have the form:
have the form:
![Rendered by QuickLaTeX.com \[ \mathrm{div}(T) = \left(\begin{array}{c} \frac{\partial T_{11}}{\partial x_1}+\frac{\partial T_{21}}{\partial x_2}+\frac{\partial T_{31}}{\partial x_3}\\ \frac{\partial T_{12}}{\partial x_1}+\frac{\partial T_{22}}{\partial x_2}+\frac{\partial T_{32}}{\partial x_3}\\ \frac{\partial T_{13}}{\partial x_1}+\frac{\partial T_{23}}{\partial x_2}+\frac{\partial T_{33}}{\partial x_3}\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cf2e6d9baeb95c45a7b1ece71ce71a34_l3.png)
Or in compact form:
![]()
It should be noted that in some texts, the divergence operator is defined as ![]() . The choice between the two definitions is a matter of convention.
. The choice between the two definitions is a matter of convention.
Curl of a Vector Field
Let ![]() be a smooth vector field. The curl of
be a smooth vector field. The curl of ![]() at a point
at a point ![]() is defined as the vector such that
is defined as the vector such that ![]() :
:
![]()
If u has the components ![]() ,
, ![]() , and
, and ![]() in an orthonormal basis set, then, by setting
in an orthonormal basis set, then, by setting ![]() ,
, ![]() , and
, and ![]() in the above formula, the components of
in the above formula, the components of ![]() are shown to have the following form:
are shown to have the following form:
![Rendered by QuickLaTeX.com \[\mbox{curl}(u)=\left(\begin{array}{c}\frac{\partial u_3}{\partial x_2}-\frac{\partial u_2}{\partial x_3}\\\frac{\partial u_1}{\partial x_3}-\frac{\partial u_3}{\partial x_1}\\\frac{\partial u_2}{\partial x_1}-\frac{\partial u_1}{\partial x_2}\end{array}\right)\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-852494a3bc03fb7494c851b84b16e47e_l3.png)
or in a compact form:
![]()
Laplacian of a Scalar Field
Let ![]() be a twice differentiable scalar field. The Lacplacian of
be a twice differentiable scalar field. The Lacplacian of ![]() denoted by
denoted by ![]() at any point
at any point ![]() is defined as the divergence of the gradient of
is defined as the divergence of the gradient of ![]() :
:
![]()
The Divergence Theorem
The divergence theorem which is also known as the Gauss’ theorem or Green’s theorem is a useful tool that relates volume integrals of gradients of functions to surface integrals of those functions. In physical terms, the divergence theorem states that the change of a continuous differentiable quantity inside a closed volume is due to the flux of this quantity entering or exiting through the boundary. The continuity ensures that there are not sinks or sources inside the volume. The mathematical theorem is as follows:
Statement
Suppose ![]() is a compact set with a piecewise smooth boundary
is a compact set with a piecewise smooth boundary ![]() and
and ![]() is the vector field defining the outward normal to the boundary
is the vector field defining the outward normal to the boundary ![]() . Let
. Let ![]() be a continuous and differentiable scalar field and
be a continuous and differentiable scalar field and ![]() ,
, ![]() ,
, ![]() define the coordinates of a point
define the coordinates of a point ![]() . Then, the divergence theorem states:
. Then, the divergence theorem states:
![Rendered by QuickLaTeX.com \[\begin{split} \int\limits_D \! \frac{\partial\phi}{\partial x_1} \,\mathrm{d}x &=\oint\limits_{S} \! \phi n_1 \,\mathrm{d}S\\ \int\limits_D \! \frac{\partial\phi}{\partial x_2} \,\mathrm{d}x &=\oint\limits_{S} \! \phi n_2 \,\mathrm{d}S\\ \int\limits_D \! \frac{\partial\phi}{\partial x_3} \,\mathrm{d}x &=\oint\limits_{S} \! \phi n_3 \,\mathrm{d}S \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fe2a79f2f942e0a8408708ec9acd3912_l3.png)
where ![]() and
and ![]() are volume and surface elements respectively.
The proof of the divergence theorem is straightforward but technical. It can be found in many vector calculus textbooks.
are volume and surface elements respectively.
The proof of the divergence theorem is straightforward but technical. It can be found in many vector calculus textbooks.
Variations
The statement of the divergence theorem above can be used to show the following consequences or variations of the divergence theorem. Assuming the same variables in the statement above and given continuous and differentiable vector and tensor fields ![]() and
and ![]() respectively then:
respectively then:
![Rendered by QuickLaTeX.com \[\begin{split} \int\limits_D \! \nabla\phi \,\mathrm{d}x &=\oint\limits_{S} \! \phi n \,\mathrm{d}S\\ \int\limits_D \! \nabla u \,\mathrm{d}x &=\oint\limits_{S} \! u\otimes n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} u \,\mathrm{d}x &=\oint\limits_{S} \! u \cdot n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} u \,\mathrm{d}x &=\oint\limits_{S} \! u \cdot n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} (\phi u) \,\mathrm{d}x &=\oint\limits_{S} \! \phi u \cdot n \,\mathrm{d}S\\ \int\limits_D \! \nabla (Tu) \,\mathrm{d}x &=\oint\limits_{S} \! (Tu)\otimes n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} T \,\mathrm{d}x &=\oint\limits_{S} \! T^T n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} (Tu) \,\mathrm{d}x &=\oint\limits_{S} \! u\cdot T^T n \,\mathrm{d}S \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-80c05a238c6c7a054a60eb181746bfb1_l3.png)
Useful Formulas
The following are useful formulas relating the various definitions above:
![Rendered by QuickLaTeX.com \[\begin{split} \mathrm{div}(\phi u) &=u\cdot \nabla \phi + \phi \mathrm{div}u\\ \mathrm{div}(T u) &=u\cdot \mathrm{div} T + \mathrm{Trace}(T\nabla u)\\ \mathrm{div}(\phi T) &=T^T\nabla \phi + \phi\mathrm{div}(T)\\ \nabla (\phi u) &=u\otimes \nabla \phi + \phi \nabla u\\ \int\limits_D \! \mbox{curl}{u} \,\mathrm{d}x &=\oint\limits_{S} \! n\times u \,\mathrm{d}S \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-86e0b4153ae7dfc499a2e8d4964cbf82_l3.png)
Note that the definitions and the results in this section can be naturally extended to ![]() for an arbitrary
for an arbitrary ![]() .
.
Comma Notation
To simplify the expressions in vector calculus, comma notation can sometimes be used to replace the expression for partial differentiation. Consider a scalar field ![]() . Then, the partial derivative of
. Then, the partial derivative of ![]() with respect to any of the components
with respect to any of the components ![]() ,
, ![]() , and
, and ![]() , can be written as:
, can be written as:
![]()
If ![]() and
and ![]() are vector and tensor fields, respectively, then, the following simplified comma notation expressions can be used (where the Einstein summation convention is also used for repeated indices):
are vector and tensor fields, respectively, then, the following simplified comma notation expressions can be used (where the Einstein summation convention is also used for repeated indices):
![Rendered by QuickLaTeX.com \[\begin{split} (\nabla u)_{ij}&=\frac{\partial u_i}{\partial x_j}=u_{i,j}\\ \mathrm{div}(u)&=\frac{\partial u_i}{\partial x_i}=u_{i,i}\\ (\mathrm{div}(T))_i&=\frac{\partial T_{ji}}{\partial x_j}=T_{ji,j}\\ (\mbox{curl}u)_i&=\varepsilon_{ijk}\frac{\partial u_k}{\partial x_j}=\varepsilon_{ijk}u_{k,i}\\ \nabla^2\phi&=\phi_{,ii} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0cf36c5d8fe7bbc98e2eb4e336b366d9_l3.png)
Examples and Problems
Example 1
Consider the set ![]() and the scalar field
and the scalar field ![]() :
:
![]()
The gradient of ![]() can be calculated as:
can be calculated as:
![]()
The following tool shows the surface plot and the contour plot of ![]() . The vector plot of
. The vector plot of ![]() is also drawn and then superimposed on top of the contour plot. Notice how the arrows are perpendicular to the contour lines! The maximum directional derivative of
is also drawn and then superimposed on top of the contour plot. Notice how the arrows are perpendicular to the contour lines! The maximum directional derivative of ![]() at the point
at the point ![]() is calculated to be along
is calculated to be along ![]() and
and ![]() . The maximum directional derivative is in the direction perpendicular to the contour line while the minimum directional derivative which is equal to zero is in the direction along (parallel) to the contour line. The tool also lets you choose a point
. The maximum directional derivative is in the direction perpendicular to the contour line while the minimum directional derivative which is equal to zero is in the direction along (parallel) to the contour line. The tool also lets you choose a point ![]() and the angle
and the angle ![]() of the direction of the vector
of the direction of the vector ![]() and calculates the directional derivative
and calculates the directional derivative ![]() at that point.
at that point.
(interactive activity placeholder) VectorCalculus/phi1.jsp
View Mathematica Code
x0 = 0;
y0 = 0;
Clear[x, y];
fi = 5 x^2-7 x (y + 3)-5 y^2;
gradfi = {D[fi, x], D[fi, y]};
gradfic = gradfi /. {x -> x0, y -> y0};
p0 = {x0, y0};
n1 = gradfic/Norm[gradfic];
n2 = {n1[[2]], -n1[[1]]};
Ar1 = Graphics[Arrow[{p0, p0 + n1}]];
Ar2 = Graphics[Arrow[{p0, p0 + n2}]];
Artext1 = Graphics[Text["n1", p0 + n1 + 0.2 n1]];
Artext2 = Graphics[Text["n2", p0 + n2 + 0.2 n2]];
a = Plot3D[fi, {x, -4, 4}, {y, -4, 4}];
b = ContourPlot[fi, {x, -4, 4}, {y, -4, 4}, ContourLabels -> True];
c = VectorPlot[gradfi, {x, -4, 4}, {y, -4, 4}];
Grid[{{"3 D Plot", "Contour Plot", "Gradient of \[Phi] plot"},
{Show[a], Show[b], Show[c]}, {"Contour Plot superimposed over Gradient of \\[Phi] plot",
SpanFromLeft}, {Show[b, c, ImageSize -> "Medium"], SpanFromLeft},
{"Directional Derviative at {0, 0} in the direction of n1 and n2", SpanFromLeft},
{Show[b, Ar1, Artext1, Ar2, Artext2, ImageSize -> "Medium"], SpanFromLeft},
{Grid[{{"\[Del]\[Phi] at (0, 0) =", gradfic // MatrixForm}},
Spacings -> 0], SpanFromLeft}, {Grid[{{"n1=", N[n1] // MatrixForm, ",\[Del]\[Phi]\[CenterDot]n1 =",
gradfic . n1}}, Spacings -> 0], SpanFromLeft}, {Grid[{{"n2 = ",
N[n2] // MatrixForm, ", \[Del]\[Phi]\[CenterDot]n2 =", gradfic . n2}}, Spacings -> 0], SpanFromLeft}}]
View Python Code
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
from sympy import diff, Matrix, lambdify
%matplotlib notebook
x,y=sp.symbols("x y")
f=5*x**2-7*x*(y+3)-5*y**2
fx=diff(f,x)
fy=diff(f,y)
v=Matrix([fx,fy])
#numpy equivalent F function
F=lambdify((x,y),f)
Fx=lambdify((x,y),fx)
Fy=lambdify((x,y),fy)
#ranges for plotting
xrange = np.arange(-4, 4, .5)
yrange = np.arange(-4, 4, .5)
X, Y = np.meshgrid(xrange, yrange)
Z = F(X,Y)
DFx=Fx(X,Y)
DFy=Fy(X,Y)
# 3D plot
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X,Y,Z)
plt.title('3D Plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# Contour plot
fig = plt.figure()
ax = fig.add_subplot(111)
cp = ax.contourf(X,Y,Z)
fig.colorbar(cp)
plt.title('Contour Plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
# Gradient plot
fig = plt.figure()
ax = fig.add_subplot(111)
ax.quiver(X, Y, DFx,DFy)
plt.title('Gradient of \u03A6 Plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
# Contour Plot superimposed over Gradient
fig = plt.figure()
ax = fig.add_subplot(111)
ax.contourf(X,Y,Z)
ax.quiver(X, Y, DFx, DFy)
plt.title('Contour Plot superimposed over Gradient of \u03A6 plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
#Directional Derviative at {0,0}
fig = plt.figure()
ax = fig.add_subplot(111)
ax.contourf(X,Y,Z)
x_0 = np.where(xrange == 0)[0][0]
y_0 = np.where(yrange == 0)[0][0]
phi = np.array([[DFx.item(x_0,y_0)],[DFy.item(x_0, y_0)] ])
ax.quiver(X[x_0, y_0], Y[x_0, y_0], DFx.item(x_0,y_0),DFy.item(x_0, y_0))
plt.title('Directional Derviative at {0,0}')
ax.set_xlabel('X')
ax.set_ylabel('Y')
#outputs
print("Delta \u03A6 at (0,0) =\n", phi)
Video
Vector Calculus Quiz
Problems
- Let
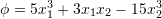 be a scalar field defined over the set
be a scalar field defined over the set
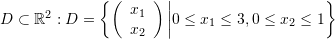 . Evaluate and indicate the order (whether it is a scalar, vector, or tensor) of the gradient of
. Evaluate and indicate the order (whether it is a scalar, vector, or tensor) of the gradient of 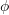 , the Laplacian of
, the Laplacian of 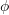 , the gradient of
, the gradient of 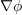 , and the divergence of the gradient of
, and the divergence of the gradient of 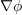 . Use Mathematica to visualize
. Use Mathematica to visualize 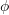 and
and 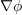 . Why is the gradient of
. Why is the gradient of 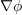 always symmetric independent of the choice of the smooth function
always symmetric independent of the choice of the smooth function 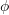 ?
? - Use the definitions in this section to show the equalities in Useful Formulas above.
- Use the divergence theorem defined above to show the last three equalities shown in the Variations of the divergence theorem shown above.
