Displacement and Strain: The Deformation and the Displacement Gradients
Learning Outcomes
- Compute the “deformation gradient” and the “displacement gradient” when given a deformation function. Identify that the “deformation gradient” and the “displacement gradient” are fundamental for calculating strain.
- Compute the small strain matrix and identify that it is the symmetric component of the displacement gradient
Definitions
For a general 3D deformation of an object, local strains can be measured by comparing the “length” between two neighbouring points before and after deformation. Thus, we are interested in tracking lines or curves on the reference and deformed configuration. The restrictions on the possible position functions ![]() (especially being differentiable) allow such comparisons and calculation as follows:
(especially being differentiable) allow such comparisons and calculation as follows:
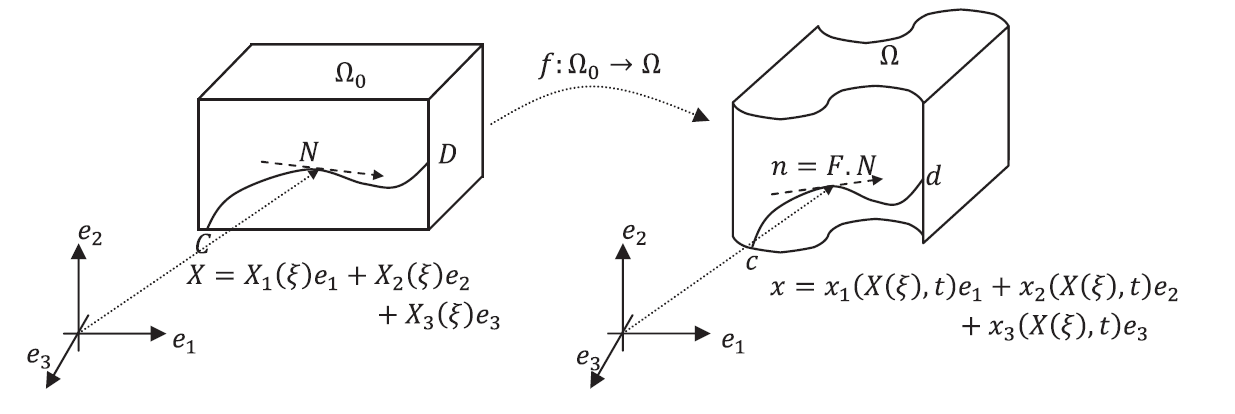
We first assume a material curve inside the reference and deformed configurations by assuming a parameter ![]() that defines the curve (Figure 1). The position in the reference and deformed configurations respectively are given by
that defines the curve (Figure 1). The position in the reference and deformed configurations respectively are given by ![]() and
and ![]() where t refers to time:
where t refers to time:
![Rendered by QuickLaTeX.com \[X = \begin{pmatrix} X_1(\xi) \\ X_2(\xi) \\ X_3(\xi) \\ \end{pmatrix} \hspace{5mm} x = \begin{pmatrix} x_1(\xi, t) \\ x_2(\xi, t) \\ x_3(\xi, t) \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-e1c5871d843ab9ff8c22522460fdd4e1_l3.png)
The tangents to the material curves at a point given by a particular value for the parameter ![]() in the reference and deformed configurations are denoted
in the reference and deformed configurations are denoted ![]() and
and ![]() respectively (Figure 1) and given by:
respectively (Figure 1) and given by:
![Rendered by QuickLaTeX.com \[N = \dfrac{\partial X}{\partial \xi} = \begin{pmatrix} \dfrac{\partial X_1}{\partial \xi} \\ \dfrac{\partial X_2}{\partial \xi} \\ \dfrac{\partial X_3}{\partial \xi} \\ \end{pmatrix} \hspace{5mm} n = \dfrac{\partial x}{\partial \xi} = \dfrac{\partial x}{\partial X} \dfrac{\partial X}{\partial \xi} = \begin{pmatrix} \dfrac{\partial x_1}{\partial X_1} & \dfrac{\partial x_1}{\partial X_2} & \dfrac{\partial x_1}{\partial X_3} \\ \dfrac{\partial x_2}{\partial X_1} & \dfrac{\partial x_2}{\partial X_2} & \dfrac{\partial x_2}{\partial X_3} \\ \dfrac{\partial x_3}{\partial X_1} & \dfrac{\partial x_3}{\partial X_2} & \dfrac{\partial x_3}{\partial X_3} \\ \end{pmatrix} \begin{pmatrix} \dfrac{\partial X_1}{\partial \xi} \\ \dfrac{\partial X_2}{\partial \xi} \\ \dfrac{\partial X_3}{\partial \xi} \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-df7181104a46d92f80ee4b20c6120b90_l3.png)
The matrix ![]() :
:
![Rendered by QuickLaTeX.com \[F = \begin{pmatrix} \dfrac{\partial x_1}{\partial X_1} & \dfrac{\partial x_1}{\partial X_2} & \dfrac{\partial x_1}{\partial X_3} \\ \dfrac{\partial x_2}{\partial X_1} & \dfrac{\partial x_2}{\partial X_2} & \dfrac{\partial x_2}{\partial X_3} \\ \dfrac{\partial x_3}{\partial X_1} & \dfrac{\partial x_3}{\partial X_2} & \dfrac{\partial x_3}{\partial X_3} \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-aa01936796c4593fabedde8f61190923_l3.png)
is denoted the “Deformation Gradient” and contains all the required local information about the changes in length, volumes and angles due to the deformation as follows:
A tangent vector N in the reference configuration is deformed into the tangent vector n. The two vectors are related using the deformation gradient tensor
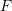 :
:
![]()
The ratio between the local volume of the deformed configuration to the local volume in the reference configuration is equal to the determinant of
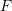 .
.If an infinitesimal area vector is termed
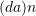 and
and 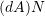 in the deformed and reference configurations respectively, with
in the deformed and reference configurations respectively, with 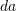 and
and 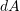 in
in 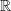 being the magnitudes of the area while
being the magnitudes of the area while  and
and 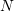 are the unit vectors perpendicular to the corresponding areas, then using Nanson’s formula shown in the section on the determinant of matrices
are the unit vectors perpendicular to the corresponding areas, then using Nanson’s formula shown in the section on the determinant of matrices  , the relationship between them is given by:
, the relationship between them is given by:An isochoric deformation is a deformation preserving local volume, i.e.,
 at every point.
at every point.A deformation is called homogeneous if
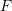 is constant at every point, i.e.,
is constant at every point, i.e., 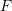 is not a function of position. Otherwise, the deformation is called non-homogeneous.
is not a function of position. Otherwise, the deformation is called non-homogeneous.The physical restrictions of possible deformations force the
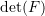 to be always positive. (why?)
to be always positive. (why?)
![]()
 and
and 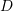 in the reference configuration correspond to points
in the reference configuration correspond to points  and
and 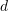 in the deformed configuration.
in the deformed configuration.The Polar Decomposition of the Deformation Gradient
One of the general results of linear algebra is the Polar Decomposition of matrices which states the following. Any matrix of real numbers ![]() can be decomposed into two matrices multiplied by each other
can be decomposed into two matrices multiplied by each other ![]() such that
such that ![]() is an orthogonal matrix and
is an orthogonal matrix and ![]() is a semi-positive definite symmetric matrix. In particular, if
is a semi-positive definite symmetric matrix. In particular, if ![]() , then we can find a rotation matrices
, then we can find a rotation matrices ![]() and two positive-definite symmetric matrices
and two positive-definite symmetric matrices ![]() and
and ![]() such that
such that
![]()
For continuum mechanics applications, ![]() and
and ![]() are termed the right and left stretch tensors respectively. The first equality is termed the “right” polar decomposition while the second is called the “left”. The proof of the above statement presented here is based on the two books:
are termed the right and left stretch tensors respectively. The first equality is termed the “right” polar decomposition while the second is called the “left”. The proof of the above statement presented here is based on the two books:
Ciarlet, P.G. (2004). Mathematical Elasticity. Volume 1: Three Dimensional Elasticity. Elsevier Ltd.
Chadwick, P. (1999). Continuum Mechanics. Concise Theory and Problems Dover Publications Inc.
and it will be presented using several statements.
Statement 1:
Let ![]() be such that
be such that ![]() . Then, the matrices
. Then, the matrices ![]() and
and ![]() are positive definite symmetric matrices.
are positive definite symmetric matrices.
PROOF:
The symmetry of ![]() and
and ![]() is straightforward as follows:
is straightforward as follows:
![]()
Also, since ![]() , therefore:
, therefore: ![]() (i.e.,
(i.e., ![]() ) we have
) we have ![]() . Therefore,
. Therefore, ![]() . Therefore,
. Therefore, ![]() is positive definite.
is positive definite.
Similarly, it can be shown that ![]() is positive definite.
is positive definite.
Statement 2:
Let ![]() be such that
be such that ![]() is a positive definite symmetric matrix. Show that there exists a unique square root positive-definite symmetric matrix for
is a positive definite symmetric matrix. Show that there exists a unique square root positive-definite symmetric matrix for ![]() (denoted by
(denoted by ![]() such that
such that ![]() .
.
PROOF:
The existence of a square root is straightforward. As per the results in the symmetric tensors section, we can choose a coordinate system such that ![]() is diagonal with three positive real numbers
is diagonal with three positive real numbers ![]() ,
, ![]() and
and ![]() in the diagonal:
in the diagonal:
![Rendered by QuickLaTeX.com \[M = \begin{pmatrix} M_1 & 0 & 0 \\ 0 & M_2 & 0 \\ 0 & 0 & M_3 \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1151f83991a4e2afb02706ef428f788e_l3.png)
By setting ![]() ,
, ![]() and
and ![]() then:
then:
![Rendered by QuickLaTeX.com \[M^{1/2} = \begin{pmatrix} \lambda_1 & 0 & 0 \\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3 \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0a6568283fdedf989e0746fbce8a3951_l3.png)
and it is straightforward to show that: ![]() in any coordinate system.
in any coordinate system.
The uniqueness of ![]() can be shown using contradiction by assuming that there are two different positive definite square roots
can be shown using contradiction by assuming that there are two different positive definite square roots ![]() and
and ![]() such that
such that
![]()
![]() is a positive-definite symmetric matrix with positive eigenvalue
is a positive-definite symmetric matrix with positive eigenvalue ![]() ,
, ![]() and
and ![]() . Let
. Let ![]() be the eigenvector associated with
be the eigenvector associated with ![]() , therefore:
, therefore:
![]()
Since by assumption, ![]() is positive definite, therefore
is positive definite, therefore ![]() is an eigenvalue of
is an eigenvalue of ![]() associated with the eigenvector
associated with the eigenvector ![]() ; otherwise,
; otherwise, ![]() is an eigenvalue of
is an eigenvalue of ![]() which contradicts that it is positive definite. This applies to
which contradicts that it is positive definite. This applies to ![]() as well and therefore,
as well and therefore, ![]() and
and ![]() are positive definite symmetric matrices that share the same eigenvalues and eigenvectors, therefore, they are identical (why?).
are positive definite symmetric matrices that share the same eigenvalues and eigenvectors, therefore, they are identical (why?).
Notice that a positive definite symmetric matrix can have various “square roots”, however, there is only one unique square root that is also a positive definite symmetric matrix. For example, consider the matrix:
![Rendered by QuickLaTeX.com \[M = \begin{pmatrix} 4 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d5eb25cb2e14c59a3efb77ee2221cf0c_l3.png)
The unique positive definite symmetric square root of ![]() is:
is:
![Rendered by QuickLaTeX.com \[M^{1/2} = \begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-81123e640e8db1f63cf3a8fb262cfff6_l3.png)
However, the following symmetric matrix ![]() is also a square root of
is also a square root of ![]() nevertheless, it is NOT positive-definite:
nevertheless, it is NOT positive-definite:
![Rendered by QuickLaTeX.com \[A = \sqrt{2} \begin{pmatrix} 1 & 1 & 0 \\ 1 & -1 & 0 \\ 0 & 0 & 1\sqrt{2} \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a16b39c8d98f674c106d390a82ea7a46_l3.png)
Verify that ![]() and
and ![]() is NOT positive-definite.
is NOT positive-definite.
Statement 3:
Let ![]() be such that
be such that ![]() Show that there exists
Show that there exists ![]() can be uniquely decomposed into:
can be uniquely decomposed into:
![]()
where, ![]() and
and ![]() are positive-definite symmetric matrices while
are positive-definite symmetric matrices while ![]() is a rotation matrix.
is a rotation matrix.
PROOF:
From the statements 1 and 2 above, ![]() and
and ![]() are unique positive definite symmetric matrices, therefore, they are invertible (why?). Let
are unique positive definite symmetric matrices, therefore, they are invertible (why?). Let
![]()
Both ![]() and
and ![]() (why?). In addition:
(why?). In addition:
![]()
and
![]()
We also have: ![]() ) and
) and ![]() , therefore,
, therefore, ![]() . Therefore,
. Therefore, ![]() . Similarly,
. Similarly, ![]() . Therefore, both,
. Therefore, both, ![]() and
and ![]() are rotation matrices.
Since
are rotation matrices.
Since ![]() and
and ![]() are invertible and unique,
are invertible and unique, ![]() and
and ![]() are also unique. We can show this by contradiction, by assuming that:
are also unique. We can show this by contradiction, by assuming that:
![]()
Therefore:
![]()
The same argument applies for ![]() .
.
Finally, it is required to show that ![]() indeed:
indeed:
![]()
However, ![]() is a positive definite symmetric matrix (why?), and since the decomposition
is a positive definite symmetric matrix (why?), and since the decomposition ![]() is unique, therefore,
is unique, therefore,
![]()
Statement 4:
![]() and
and ![]() share the same eigenvalues and their eigenvectors differ by the rotation
share the same eigenvalues and their eigenvectors differ by the rotation ![]()
PROOF:
Assuming that ![]() is an eigenvalue of
is an eigenvalue of ![]() with the corresponding eigenvector
with the corresponding eigenvector ![]() , then:
, then:
![]()
Therefore, ![]() is an eigenvalue of
is an eigenvalue of ![]() while
while ![]() is the associated eigenvector.
is the associated eigenvector.
Similarly, if ![]() is an eigenvalue of
is an eigenvalue of ![]() with the corresponding eigenvector
with the corresponding eigenvector ![]() , then:
, then:
![]()
Therefore, ![]() is an eigenvalue of
is an eigenvalue of ![]() while
while ![]() is the associated eigenvector.
Assuming that
is the associated eigenvector.
Assuming that ![]() ,
, ![]() and
and ![]() are the eigenvalues of
are the eigenvalues of ![]() and
and ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are the associated eigenvectors of
are the associated eigenvectors of ![]() , while
, while ![]() ,
, ![]() , and
, and ![]() are the associated eigenvectors of
are the associated eigenvectors of ![]() , then
, then ![]() and
and ![]() admit the representations (see the section about the representation of symmetric matrices):
admit the representations (see the section about the representation of symmetric matrices):
![]()
![]()
and ![]() :
:
![]()
Physical Interpretation
The unique decomposition of the deformation gradient ![]() into a rotation and a stretch indicates that any smooth deformation can be decomposed at any point inside the continuum body into a unique stretch described by
into a rotation and a stretch indicates that any smooth deformation can be decomposed at any point inside the continuum body into a unique stretch described by ![]() followed by a unique rotation described by
followed by a unique rotation described by ![]() . For example, a circle representing the directions of all the vectors in
. For example, a circle representing the directions of all the vectors in ![]() is deformed into an ellipse under the action of
is deformed into an ellipse under the action of ![]() where
where ![]() . The decomposition
. The decomposition ![]() is schematically shown by first stretching the circle into an ellipse whose major axes are the eigenvectors of
is schematically shown by first stretching the circle into an ellipse whose major axes are the eigenvectors of ![]() followed by a rotation of the ellipse through the matrix
followed by a rotation of the ellipse through the matrix ![]() . The decomposition
. The decomposition ![]() represents rotating the circle through the matrix
represents rotating the circle through the matrix ![]() and then stretching the circle into an ellipse whose major axes are the eigenvectors of
and then stretching the circle into an ellipse whose major axes are the eigenvectors of ![]() . Notice that the eigenvectors of
. Notice that the eigenvectors of ![]() and the eigenvectors of
and the eigenvectors of ![]() differ by a mere rotation. In the following tool, change the values of the four components of the matrix
differ by a mere rotation. In the following tool, change the values of the four components of the matrix ![]() . The code first ensures that
. The code first ensures that ![]() . Once this condition is satisfied, the tool draws the two steps of the right polar decomposition in the first row and then the steps of the left polar decomposition in the second row. In the first image on the first row, the arrows indicate the eigenvectors of
. Once this condition is satisfied, the tool draws the two steps of the right polar decomposition in the first row and then the steps of the left polar decomposition in the second row. In the first image on the first row, the arrows indicate the eigenvectors of ![]() . The arrows are shown to deform but keep their direction in the second image of the first row. Then, after applying the rotation, the arrows rotate in the third image of the first row. In the second image of the second row, the arrows are rotated with the matrix
. The arrows are shown to deform but keep their direction in the second image of the first row. Then, after applying the rotation, the arrows rotate in the third image of the first row. In the second image of the second row, the arrows are rotated with the matrix ![]() without any change in length. Then, they are deformed using the matrix
without any change in length. Then, they are deformed using the matrix ![]() in the third image of the second row.
in the third image of the second row.
The Singular-Value Decomposition of the Deformation Gradient
One of the general results of linear algebra is the Singular-Value Decomposition of real or complex matrices. When the statement is applied to a matrix ![]() with
with ![]() it states that
it states that
![]()
Where, ![]() and
and ![]() are rotation matrices while the matrix
are rotation matrices while the matrix ![]() is a diagonal matrix with positive diagonal entries. The singular-value decomposition follows immediately from the previous section on the polar decomposition of the deformation gradient. By setting
is a diagonal matrix with positive diagonal entries. The singular-value decomposition follows immediately from the previous section on the polar decomposition of the deformation gradient. By setting ![]() and realizing that
and realizing that ![]() is a positive definite symmetric matrix, then using the spectral form of symmetric tensors
is a positive definite symmetric matrix, then using the spectral form of symmetric tensors ![]() can be decomposed such that
can be decomposed such that ![]() where
where ![]() is a diagonal matrix whose diagonal entries are positive and
is a diagonal matrix whose diagonal entries are positive and ![]() is a rotation matrix whose columns are the normalized eigenvectors of
is a rotation matrix whose columns are the normalized eigenvectors of ![]() (The rows of
(The rows of ![]() are the normalized eigenvectors of
are the normalized eigenvectors of ![]() ). In particular, they are the square roots of the eigenvalues of the positive definite symmetric matrix
). In particular, they are the square roots of the eigenvalues of the positive definite symmetric matrix ![]() . Therefore:
. Therefore:
![]()
By setting ![]() we get the required result:
we get the required result:
![]()
The following tool calculates the polar decomposition and the singular value decomposition of a matrix ![]() . Enter the values for the components of
. Enter the values for the components of ![]() and the tool calculates all the required matrices after checking that
and the tool calculates all the required matrices after checking that ![]() .
.
The Right Cauchy-Green Deformation Tensor
The tensor![]() is termed the right Cauchy-Green deformation tensor. As shown above, it is a positive definite symmetric matrix, thus, it has three positive real eigenvalues and three perpendicular eigenvectors. It also has a unique positive square root
is termed the right Cauchy-Green deformation tensor. As shown above, it is a positive definite symmetric matrix, thus, it has three positive real eigenvalues and three perpendicular eigenvectors. It also has a unique positive square root ![]() (See statement 2 above) such that
(See statement 2 above) such that ![]() has the same eigenvectors, while the eigenvalues of
has the same eigenvectors, while the eigenvalues of ![]() are the positive square roots of the eigenvalues of
are the positive square roots of the eigenvalues of ![]() . Denote
. Denote ![]() ,
, ![]() , and
, and ![]() as the eigenvalues of
as the eigenvalues of ![]() with the corresponding eigenvectors
with the corresponding eigenvectors ![]() ,
, ![]() and
and ![]() , then
, then ![]() ,
, ![]() and
and ![]() admit the representations (see the section about the representation of symmetric matrices):
admit the representations (see the section about the representation of symmetric matrices):
![]()
![]()
![]()
It is worth noting that the last expression for ![]() is equivalent to the singular-value decomposition of
is equivalent to the singular-value decomposition of ![]() described above. The singular-value decomposition,
described above. The singular-value decomposition, ![]() where
where ![]() is a rotation matrix whose columns are the eigenvectors of
is a rotation matrix whose columns are the eigenvectors of ![]() , is more convenient for component calculations, while the last expression with tensor product is much more useful for formula manipulation.
, is more convenient for component calculations, while the last expression with tensor product is much more useful for formula manipulation.
The Left Cauchy-Green Deformation Tensor:
The tensor ![]() is termed the left Cauchy-Green deformation tensor. As shown above, it is a positive definite symmetric matrix, thus, it has three positive real eigenvalues and three perpendicular eigenvectors. It also has a unique positive square root
is termed the left Cauchy-Green deformation tensor. As shown above, it is a positive definite symmetric matrix, thus, it has three positive real eigenvalues and three perpendicular eigenvectors. It also has a unique positive square root ![]() (See statement 2 above) such that
(See statement 2 above) such that ![]() has the same eigenvectors, while the eigenvalues of
has the same eigenvectors, while the eigenvalues of ![]() are the positive square roots of the eigenvalues of
are the positive square roots of the eigenvalues of ![]() . From statement 2 and statement 4 above, the eigenvalues of
. From statement 2 and statement 4 above, the eigenvalues of ![]() and
and ![]() are the same while the eigenvectors differ by the rotation
are the same while the eigenvectors differ by the rotation ![]() (why?). Denote
(why?). Denote ![]() ,
, ![]() , and
, and ![]() as the eigenvalues of
as the eigenvalues of ![]() with the corresponding eigenvectors
with the corresponding eigenvectors ![]() ,
, ![]() and
and ![]() , then
, then ![]() ,
, ![]() and
and ![]() admit the representations (see the section about the representation of symmetric matrices):
admit the representations (see the section about the representation of symmetric matrices):
![]()
![]()
![]()
By utilizing the properties of the tensor product , the following alternative representation of ![]() can be obtained:
can be obtained:
![]()
Also, since ![]() ,
, ![]() , and
, and ![]() are orthonormal, then
are orthonormal, then ![]() . Therefore:
. Therefore:
![]()
By utilizing the properties of the tensor product:
![]()
Therefore:
![]()
The Displacement Gradient Tensor
Another three dimensional measure of deformation is the displacement gradient tensor. The displacement gradient tensor appears naturally when we attempt to write the relationship between a tangent vector ![]() in the reference configuration deformation and its image under deformation
in the reference configuration deformation and its image under deformation ![]() such that:
such that:
![]()
where ![]() is the “displacement” vector that describes the change in tangent vectors.
is the “displacement” vector that describes the change in tangent vectors.
As discussed in the deformation gradient section, ![]() and
and ![]() are related as follows:
are related as follows:
![]()
Therefore, the “displacement” vector ![]() can be written as:
can be written as:
![]()
The tensor ![]() is denoted the displacement gradient tensor and can be written in component form as follows:
is denoted the displacement gradient tensor and can be written in component form as follows:
![Rendered by QuickLaTeX.com \[\nabla u = \begin{pmatrix} \dfrac{\partial u_1}{\partial X_1} & \dfrac{\partial u_1}{\partial X_2} & \dfrac{\partial u_1}{\partial X_3} \\ \dfrac{\partial u_2}{\partial X_1} & \dfrac{\partial u_2}{\partial X_2} & \dfrac{\partial u_2}{\partial X_3} \\ \dfrac{\partial u_3}{\partial X_1} & \dfrac{\partial u_3}{\partial X_2} & \dfrac{\partial u_3}{\partial X_3} \\ \end{pmatrix} = \begin{pmatrix} \dfrac{\partial x_1}{\partial X_1} & \dfrac{\partial x_1}{\partial X_2} & \dfrac{\partial x_1}{\partial X_3} \\ \dfrac{\partial x_2}{\partial X_1} & \dfrac{\partial x_2}{\partial X_2} & \dfrac{\partial x_2}{\partial X_3} \\ \dfrac{\partial x_3}{\partial X_1} & \dfrac{\partial x_3}{\partial X_2} & \dfrac{\partial x_3}{\partial X_3} \\ \end{pmatrix} - \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b8bffd578ef45b5908de64739450750c_l3.png)
As described in the skewsymmetric tensors section, every tensor can be uniquely decomposed into two additive components, a symmetric tensor and a skewsymmetric tensor. By denoting the symmetric part as \varepsilon or the “infinitesimal strain tensor” and the skewsymmetric part as ![]() or the “infintesimal rotation tensor” we can write the relationship between the vectors in the reference and deformed configuration as follows:
or the “infintesimal rotation tensor” we can write the relationship between the vectors in the reference and deformed configuration as follows:
![]()
In other words, the additive decomposition of the displacement gradient tensor allows to write the deformed vector ![]() as the additive combination of three vectors: the original vector
as the additive combination of three vectors: the original vector ![]() , plus a “strain” or “stretch” component
, plus a “strain” or “stretch” component ![]() , plus a “rotation” component
, plus a “rotation” component ![]() . The stretch component can be calculated using the symmetric tensor
. The stretch component can be calculated using the symmetric tensor ![]() while the rotation component can be calculated using the skewsymmetric tensor
while the rotation component can be calculated using the skewsymmetric tensor ![]() . Both tensors are physically meaningful when
. Both tensors are physically meaningful when ![]() has very small components
has very small components ![]() (small displacements).
(small displacements).
