Approximate Methods: The Rayleigh Ritz Method: Problems
- The exact displacement in meters of the shown Euler Bernoulli beam follows the function:
The beam’s Young’s modulus and moment of inertia are![Rendered by QuickLaTeX.com \[ y=\begin{cases} 0.0003375X_1^2(3X_1-20) & 0\leq X_1\leq 5\\ -0.0003125(X_1-8)^2(7X_1-20) & 5< X_1\leq 8 \end{cases} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-705fa07d7d9f233d9bff47a42dada63c_l3.png)
 and
and  .
.
- Find the strain energy stored in the beam (Answer: 21093.8 N.m.).
- Use the Rayleigh Ritz method to find approximate solutions for the displacement across the whole beam. Assume the approximations to be polynomials of the zero, first, second, third, fourth, fifth, and sixth degrees.
- Plot the exact solution versus the approximate solutions for
 ,
,  ,
,  , and
, and 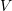 . Comment on the results.
. Comment on the results.
-
For the following two linear elastic isotropic small deformations beam structures:
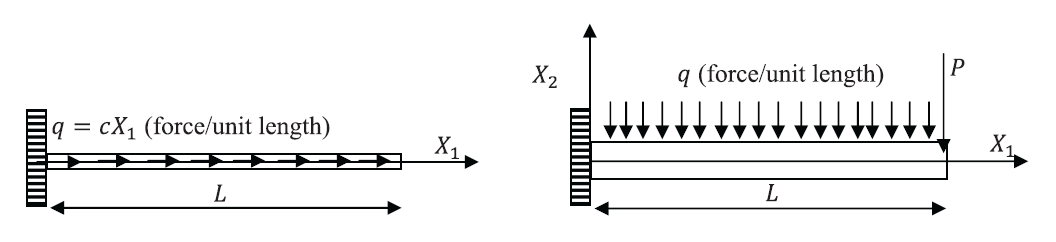
- Find the exact solution of the displacement.
- Find an approximate solution using the Rayleigh Ritz method with polynomial trial functions of zero, first, second, third, and fourth degrees satisfying the essential boundary conditions. Comment on the difference between the approximate and the exact solutions.
-
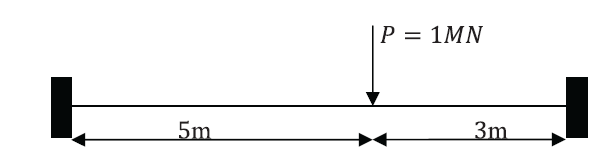
An Euler Bernoulli beam of length
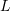 with both ends fixed is loaded by a concentrated force
with both ends fixed is loaded by a concentrated force  at the centre of the beam. Assume that the beam is made out of a linear elastic isotropic material and that the deformations are small. If
at the centre of the beam. Assume that the beam is made out of a linear elastic isotropic material and that the deformations are small. If 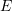 is Young’s modulus and
is Young’s modulus and 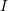 is the moment of inertia, then find:
is the moment of inertia, then find:
- the strain energy in terms of the displacement function
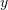 .
. - The expression for the potential energy of the system.
- Show that the following series satisfies the essential boundary conditions
where![Rendered by QuickLaTeX.com \[ w=\sum_{n=2}^\infty A_n\left(\cos{\frac{n\pi x}{L}}-1\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-3b208b1f699e28c723f8d21e6c2f8cb3_l3.png)
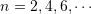 and
and 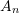 are constants
are constants - Take one term and two terms from the series above and determine the constants using the Rayleigh Ritz method.
- Find the exact solution and compare with the approximate solutions obtained using the Rayleigh Ritz method.
- the strain energy in terms of the displacement function
-
For the shown two beam structures

- Find the exact solution for the displacement.
- Use the Rayleigh Ritz method with polynomials of the zero, one, two, three, four, five, and six degrees to find an approximate solution for the displacement. For the beam under axial loading compare the stresses with the exact solution. For the beam under lateral loading, compare the rotation, moment, and shear with the corresponding exact solutions.
-
The shown beam under axial loading is subjected to the varying body force given per unit volume. Assume that the area varies linearly across the length of the structure.

- Find the exact displacement by solving the differential equation of equilibrium for bars under axial loading.
- Use the Rayleigh Ritz method to find a polynomial approximation of the zero, first, second, and third degrees for the displacement function.
-
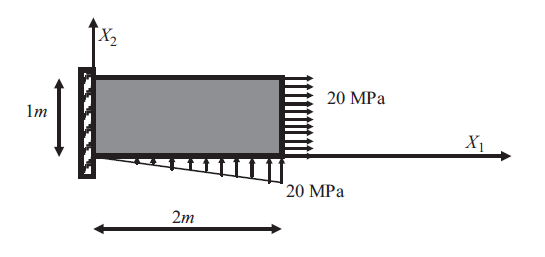
The shown plate has a thickness
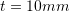 . The plate is in a plane stress condition. The left boundary where
. The plate is in a plane stress condition. The left boundary where 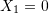 has zero vertical and horizontal displacements. The material is linear elastic with small deformations and Young’s modulus
has zero vertical and horizontal displacements. The material is linear elastic with small deformations and Young’s modulus 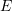 and Poisson’s ratio
and Poisson’s ratio  are equal to 200 GPa and 0.3, respectively. The right boundary is subjected to a constant normal tensile stress of 20MPa while the bottom boundary is subjected to a normal compressive stress that varies linearly with a maximum value of 20MPa as shown in the figure below. Using the Rayleigh Ritz method and assuming that the displacement of the plate can be approximated using the function:
are equal to 200 GPa and 0.3, respectively. The right boundary is subjected to a constant normal tensile stress of 20MPa while the bottom boundary is subjected to a normal compressive stress that varies linearly with a maximum value of 20MPa as shown in the figure below. Using the Rayleigh Ritz method and assuming that the displacement of the plate can be approximated using the function:
![Rendered by QuickLaTeX.com \[ u=\left(\begin{array}{c}a_0+a_1X_1+a_2X_2+a_3X_1X_2\\b_0+b_1X_1+b_2X_2+b_3X_1X_2\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-27c3ddd7f66caa29121e1c07d2136b84_l3.png)
- Utilize the essential boundary conditions to reduce the number of unknown constants in the displacement function.
- Find the infinitesimal strain tensor in terms of the remaining unknown constants.
- Write the expression of the potential energy of the system in terms of the remaining unknown constants.
- Find the unknown constants using the Rayleigh Ritz method.
- Comment on how accurate the above displacement function is in approximating the exact displacement of the plate.
-
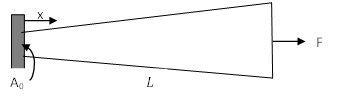
Consider a uniaxial bar of length
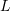 , Young’s modulus
, Young’s modulus 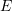 , and variable cross sectional area
, and variable cross sectional area 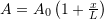 . The bar is fixed at one end and free at the other end. The free end is subjected to a constant force F. Using the Rayleigh Ritz method, and assuming a trial parabolic displacement function
. The bar is fixed at one end and free at the other end. The free end is subjected to a constant force F. Using the Rayleigh Ritz method, and assuming a trial parabolic displacement function 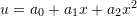 , determine the approximate displacement function of the bar. Compare the results with the exact solution given by:
, determine the approximate displacement function of the bar. Compare the results with the exact solution given by:
![Rendered by QuickLaTeX.com \[ u=\frac{FL}{EA_0}\ln\left(1+\frac{x}{L}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cf6f92793ccb28001ffbf1863ae84798_l3.png)
-
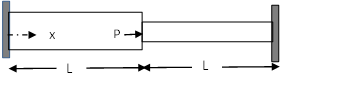
Two bars joined at
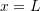 are subjected to a force
are subjected to a force  at the joint. The cross sectional area of the larger bar is twice that of the smaller bar. Use the Rayleigh Ritz method with a trial displacement function of
at the joint. The cross sectional area of the larger bar is twice that of the smaller bar. Use the Rayleigh Ritz method with a trial displacement function of 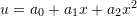 to approximate the exact displacement of the bar. Assume the area of the smaller bar to be equal to
to approximate the exact displacement of the bar. Assume the area of the smaller bar to be equal to 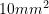 ,
, 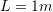 ,
, 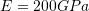 , and
, and 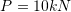 . Compare with the exact displacement field.
. Compare with the exact displacement field.
-
A beam of length
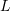 Young’s modulus
Young’s modulus 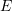 , and moment of inertia
, and moment of inertia 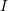 is fixed at both ends and subjected to a uniformly distributed load
is fixed at both ends and subjected to a uniformly distributed load 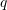 and a concentrated force
and a concentrated force  at midspan. Use the Rayligh Ritz method with a trial function
at midspan. Use the Rayligh Ritz method with a trial function 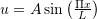 where
where 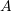 is a real number to approximate the midspan deflection of the beam.
is a real number to approximate the midspan deflection of the beam.
-
Consider a uniaxial bar of length
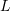 , Young’s modulus
, Young’s modulus 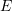 , and variable cross sectional area
, and variable cross sectional area 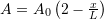 . The bar is fixed at one end and free at the other end. The free end is subjected to a constant force
. The bar is fixed at one end and free at the other end. The free end is subjected to a constant force  and a uniformly distributed force
and a uniformly distributed force 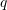 . Using the Rayleigh Ritz method, and assuming a quadratic trial displacement function, determine the approximate displacement of the bar.
. Using the Rayleigh Ritz method, and assuming a quadratic trial displacement function, determine the approximate displacement of the bar.

