Calculus: Vector Calculus in Cylindrical Coordinate Systems
Introduction
Polar Coordinate System
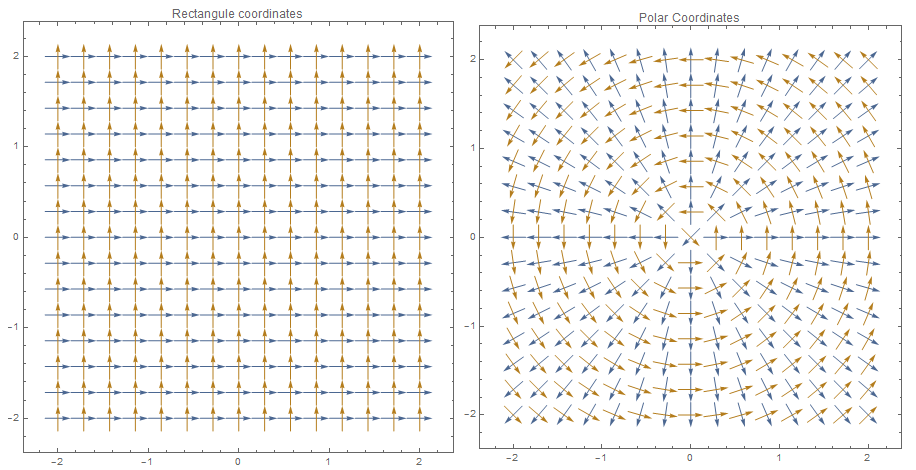
Consider the representation of a geometric plane using ![]() with a chosen but arbitrary origin. The directions at every point in the plane are defined using the basis vectors
with a chosen but arbitrary origin. The directions at every point in the plane are defined using the basis vectors ![]() and
and ![]() (Fig 1 left). In certain situations, it is more convenient to define directions or basis vectors at every point such that the first direction (first basis vector) points away from the origin (blue arrows in Fig 1 right) and the second direction is perpendicular to the first direction while maintaining the right hand rule (yellow arrows in Fig 1 right). Given that the coordinates of a point in the geometric plane are given by
(Fig 1 left). In certain situations, it is more convenient to define directions or basis vectors at every point such that the first direction (first basis vector) points away from the origin (blue arrows in Fig 1 right) and the second direction is perpendicular to the first direction while maintaining the right hand rule (yellow arrows in Fig 1 right). Given that the coordinates of a point in the geometric plane are given by ![]() and
and ![]() , then, we can define at every point the following relations:
, then, we can define at every point the following relations:
![]()
with the inverse relationship:
![Rendered by QuickLaTeX.com \[\begin{split} r&=\sqrt{x_1^2+x_2^2}\\ \theta&=\arctan[x_1,x_2] \end{split}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c71a2e577a8596968b28e635d23e9579_l3.png)
taking into consideration the quadrant of ![]() and
and ![]() . It is important to note that the function
. It is important to note that the function ![]() is not defined at the origin. It is also important to note that
is not defined at the origin. It is also important to note that ![]() and
and ![]() are themselves vector fields.
are themselves vector fields. ![]() represents a vector field of unit vectors that are pointing away from the origin and
represents a vector field of unit vectors that are pointing away from the origin and ![]() represents a vector field of unit vectors perpendicular to the vectors of the
represents a vector field of unit vectors perpendicular to the vectors of the ![]() vector field maintaining the right hand orientation (Fig 1 left). Using a simple change of coordinates, the new basis set
vector field maintaining the right hand orientation (Fig 1 left). Using a simple change of coordinates, the new basis set ![]() at a point represented by the coordinates
at a point represented by the coordinates ![]() and
and ![]() (or the corresponding r and \theta) can be related to the Cartesian basis
(or the corresponding r and \theta) can be related to the Cartesian basis ![]() and
and ![]() using the relationships:
using the relationships:
![]()
Therefore, the coordinate transformation from the Cartesian basis to the polar coordinate system is described at every point using the matrix ![]() :
:
![]()
As the vector fields ![]() and
and ![]() are functions of the two real numbers
are functions of the two real numbers ![]() , and
, and ![]() , then, we can find the derivatives of
, then, we can find the derivatives of ![]() and
and ![]() as follows:
as follows:
![]()
![]()
It is also useful to find the derivatives of the position vector of a point with respect to the independent variables ![]() and
and ![]() . The position
. The position ![]() of a point in the plane is given by:
of a point in the plane is given by:
![]()
The derivatives of the position vector with respect to ![]() and
and ![]() are given by:
are given by:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\partial x}{\partial r}&=e_r(\theta)\\ \frac{\partial x}{\partial \theta}&=re_\theta(\theta) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1c4300ebbc736ec9e335f4a696ff7e48_l3.png)
These derivatives will be used to calculate the derivatives of other quantities in a polar coordinate system.
Cylindrical Coordinate System:
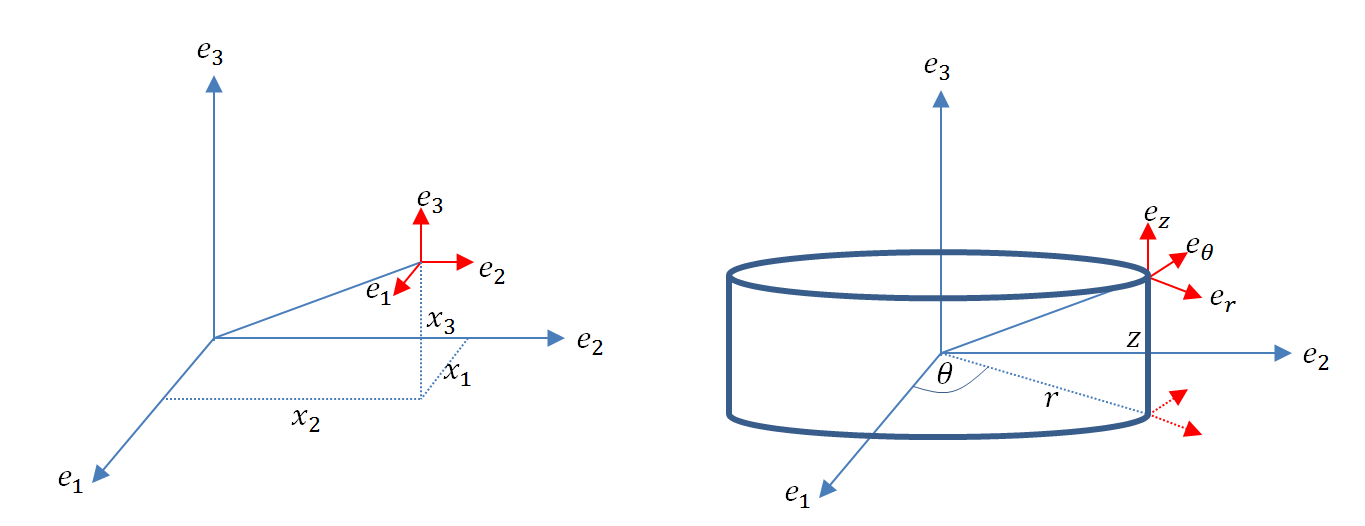
A cylindrical coordinate system is a system used for directions in \mathbb{R}^3 in which a polar coordinate system is used for the first plane (Fig 2 and Fig 3). The coordinate system directions can be viewed as three vector fields ![]() , and
, and ![]() such that:
such that:
![Rendered by QuickLaTeX.com \[\begin{split} e_r&=\cos(\theta)e_1+\sin(\theta)e_2\\ e_\theta&=-\sin(\theta)e_1+\cos(\theta)e_2\\ e_z&=e_3 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-42f259204b4cfb32afeb68247f3399dd_l3.png)
with ![]() and
and ![]() related to the coordinates
related to the coordinates ![]() and
and ![]() using the polar coordinate system relationships. The coordinate transformation from the Cartesian basis to the cylindrical coordinate system is described at every point using the matrix
using the polar coordinate system relationships. The coordinate transformation from the Cartesian basis to the cylindrical coordinate system is described at every point using the matrix ![]() :
:
![Rendered by QuickLaTeX.com \[ Q=\left(\begin{matrix}\cos(\theta)&\sin(\theta)&0\\-\sin(\theta)&\cos(\theta)&0\\0&0&1\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-57d5dad712634870ad395bf6e0c38eb9_l3.png)
The vector fields ![]() and
and ![]() are functions of
are functions of ![]() and their derivatives with respect to
and their derivatives with respect to ![]() and
and ![]() follow from the polar coordinate system.
follow from the polar coordinate system. ![]() on the other hand is independent of
on the other hand is independent of ![]() and
and ![]() .
.
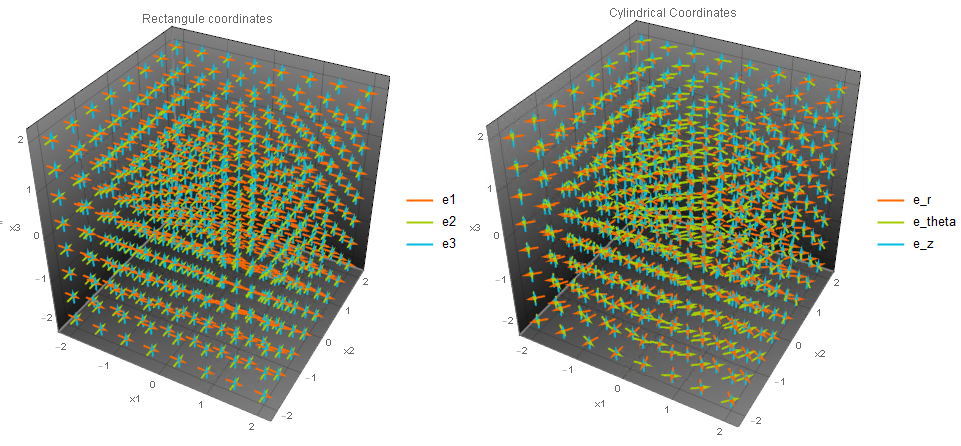
Fields in Cylindrical Coordinate System
Let ![]() be a subset of
be a subset of ![]() . If
. If ![]() ,
, ![]() , and
, and ![]() are smooth scalar, vector and second-order tensor fields, then they can be chosen to be functions of either the Cartesian coordinates
are smooth scalar, vector and second-order tensor fields, then they can be chosen to be functions of either the Cartesian coordinates ![]() , and
, and ![]() , or the corresponding real numbers
, or the corresponding real numbers ![]() ,
, ![]() , and
, and ![]() . Also,
. Also, ![]() and
and ![]() can have their components expressed in either the fixed orthonormal basis set
can have their components expressed in either the fixed orthonormal basis set ![]() , or can be expressed using the cylindrical coordinate system directions at every point. In other words,
, or can be expressed using the cylindrical coordinate system directions at every point. In other words, ![]() , as a vector field, can have the one of the following forms:
, as a vector field, can have the one of the following forms:
![Rendered by QuickLaTeX.com \[\begin{split} u(x_1,x_2,x_3)&=u_1(x_1,x_2,x_3)e_1+u_2(x_1,x_2,x_3)e_2+u_3(x_1,x_2,x_3)e_3\\ &=u(r,\theta,z)\\ &=u_r(r,\theta,z)e_r(\theta)+u_\theta(r,\theta,z)e_\theta(\theta)+u_z(r,\theta,z)e_z \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0fa90eab3a6e17ea210a10df671f0f12_l3.png)
where ![]() , and
, and ![]() are scalar fields. Similarly,
are scalar fields. Similarly, ![]() , as a tensor field, can have one of the following forms:
, as a tensor field, can have one of the following forms:
![Rendered by QuickLaTeX.com \[\begin{split} T(x_1,x_2,x_3)&=T_{11}(x_1,x_2,x_3)e_1\otimes e_1+T_{12}(x_1,x_2,x_3)e_1\otimes e_2+T_{13}(x_1,x_2,x_3)e_1\otimes e_3\\ & +T_{21}(x_1,x_2,x_3)e_2\otimes e_1+T_{22}(x_1,x_2,x_3)e_2\otimes e_2+T_{23}(x_1,x_2,x_3)e_2\otimes e_3\\ & +T_{31}(x_1,x_2,x_3)e_3\otimes e_1+T_{32}(x_1,x_2,x_3)e_3\otimes e_2+T_{33}(x_1,x_2,x_3)e_3\otimes e_3\\ &=T(r,\theta,z)\\ &=T_{rr}(r,\theta,z)e_r(\theta)\otimes e_r(\theta)+T_{r\theta}(r,\theta,z)e_r(\theta)\otimes e_\theta(\theta)+T_{rz}(r,\theta,z)e_r(\theta)\otimes e_z\\ & +T_{\theta r}(r,\theta,z)e_\theta(\theta)\otimes e_r(\theta)+T_{\theta \theta}(r,\theta,z)e_\theta(\theta)\otimes e_\theta(\theta)+T_{\theta z}(r,\theta,z)e_\theta(\theta)\otimes e_z\\ & +T_{zr}(r,\theta,z)e_z\otimes e_r(\theta)+T_{z\theta}(r,\theta,z)e_z\otimes e_\theta(\theta)+T_{zz}(r,\theta,z)e_z\otimes e_z \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-40a5bcfebbf20f7ca79a9e75f88d228b_l3.png)
where ![]() , and
, and ![]() are scalar fields.
are scalar fields.
Field Derivatives in Cylindrical Coordinate Systems
Gradient of a Scalare Field
Let ![]() be a scalar field such that
be a scalar field such that ![]() . The gradient of
. The gradient of ![]() in a cylindrical coordinate system can be obtained using one of two ways. The first way is to find
in a cylindrical coordinate system can be obtained using one of two ways. The first way is to find ![]() as a function of
as a function of ![]() , and
, and ![]() by simply replacing
by simply replacing ![]() ,
,![]() , and
, and ![]() . Then, finding the gradient of
. Then, finding the gradient of ![]() in the Cartesian coordinate system and then utilizing the relationship
in the Cartesian coordinate system and then utilizing the relationship ![]() . After that, the variables
. After that, the variables ![]() , and
, and ![]() can be replaced with
can be replaced with ![]() , and
, and ![]() . Alternative, the gradient of
. Alternative, the gradient of ![]() can be obtained directly in the cylindrical coordinate system. In order to find the expression for the gradient, recall that a scalar field
can be obtained directly in the cylindrical coordinate system. In order to find the expression for the gradient, recall that a scalar field ![]() is differentiable if there exists
is differentiable if there exists ![]() such that
such that ![]() ,
, ![]()
![]()
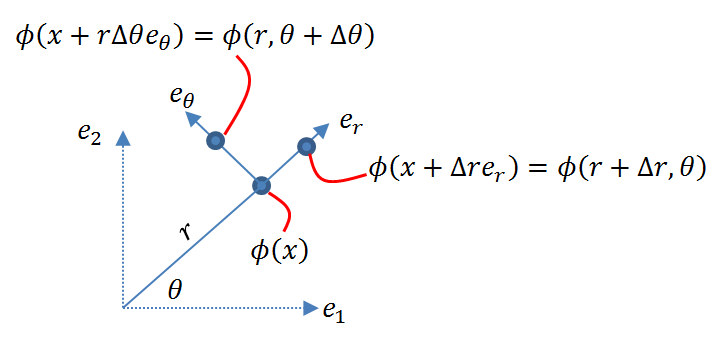
Using this definition, we will aim to find the representation of ![]() in a cylindrical coordinate system. Let
in a cylindrical coordinate system. Let ![]() . We will strategically choose particular expressions for hn to obtain the required expression for the vector
. We will strategically choose particular expressions for hn to obtain the required expression for the vector ![]() . First, we will choose hn such that it is equivalent to a path increment caused by a change \Delta r, i.e., hn=\Delta r \frac{\partial x}{\partial r}=\Delta r e_r (Fig. 4). Then:
. First, we will choose hn such that it is equivalent to a path increment caused by a change \Delta r, i.e., hn=\Delta r \frac{\partial x}{\partial r}=\Delta r e_r (Fig. 4). Then:
![]()
Therefore:
![]()
Therefore:
![]()
Similarly, ![]() can be chosen to be equivalent to a path increment caused by
can be chosen to be equivalent to a path increment caused by ![]() , i.e.,
, i.e., ![]() (Fig. 4). Therefore:
(Fig. 4). Therefore:
![]()
Therefore:
![]()
Therefore:
![]()
Therefore,
![]()
The third component is straightforward and is equal to:
![]()
Therefore, the gradient of ![]() in a cylindrical coordinate system has the form:
in a cylindrical coordinate system has the form:
![]()
Gradient of a Vector Field
Let ![]() be a smooth vector field. The components of the tensor field
be a smooth vector field. The components of the tensor field ![]() in a cylindrical coordinate system can be obtained by a simple coordinate transformation using the components in the Cartesian coordinate system and the matrix of transformation
in a cylindrical coordinate system can be obtained by a simple coordinate transformation using the components in the Cartesian coordinate system and the matrix of transformation ![]() . I.e.,
. I.e., ![]() . Alternatively, if
. Alternatively, if ![]() is already expressed in a cylindrical coordinate system, then, notice that the derivatives of
is already expressed in a cylindrical coordinate system, then, notice that the derivatives of ![]() with respect to
with respect to ![]() ,
, ![]() , and
, and ![]() are given by:
are given by:
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\partial u}{\partial r}&=\frac{\partial u_r}{\partial r}e_r+\frac{\partial u_\theta}{\partial r}e_\theta+\frac{\partial u_z}{\partial r}e_z\\ \frac{\partial u}{\partial \theta}&=\frac{\partial u_r}{\partial \theta}e_r+u_r e_\theta+\frac{\partial u_\theta}{\partial \theta}e_\theta-u_{\theta}e_r+\frac{\partial u_z}{\partial \theta}e_z\\ \frac{\partial u}{\partial z}&=\frac{\partial u_r}{\partial z}e_r+\frac{\partial u_\theta}{\partial z}e_\theta+\frac{\partial u_z}{\partial z}e_z \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-449586bae4d36c4faff44fd683a6e805_l3.png)
We can now assume assume that, in the cylindrical coordinate system, ![]() has the following form:
has the following form:
![Rendered by QuickLaTeX.com \[ \nabla u'=\left(\begin{matrix}\nabla u_{rr} & \nabla u_{r\theta} & \nabla u_{rz}\\ \nabla u_{\theta r} & \nabla u_{\theta \theta} & \nabla u_{\theta z}\\\nabla u_{zr} & \nabla u_{z\theta} & \nabla u_{zz} \end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c804d0d565b5a460728d665e05940737_l3.png)
Notice that:
![Rendered by QuickLaTeX.com \[\begin{split} \nabla u_{rr}&=\nabla u e_r\cdot e_r\\ \nabla u_{r\theta}&=\nabla u e_\theta \cdot e_r\\ \nabla u_{rz}&=\nabla u e_z \cdot e_r\\ \nabla u_{\theta r}&=\nabla u e_r\cdot e_\theta \\ \nabla u_{\theta \theta}&=\nabla u e_\theta \cdot e_\theta \\ \nabla u_{\theta z}&=\nabla u e_z \cdot e_\theta \\ \nabla u_{z r}&=\nabla u e_r\cdot e_z \\ \nabla u_{z \theta}&=\nabla u e_\theta \cdot e_z \\ \nabla u_{z z}&=\nabla u e_z \cdot e_z \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-49b8b88f9d807d341ad57b7f0fb62f7d_l3.png)
Recall that a vector field is differentiable if there exists a tensor field denoted ![]() such that
such that ![]() :
:
![]()
Therefore, the component ![]() can be obtained by setting
can be obtained by setting ![]() in the above relationship and taking the dot product with
in the above relationship and taking the dot product with ![]() as follows:
as follows:
![]()
I.e.
![]()
Therefore:
![]()
The component ![]() can be obtained by setting
can be obtained by setting ![]() in the above relationship and taking the dot product with
in the above relationship and taking the dot product with ![]() as follows:
as follows:
![]()
I.e.
![]()
Therefore:
![]()
Similarly,
![Rendered by QuickLaTeX.com \[\begin{split} \nabla u_{\theta r}&=\frac{\partial u_\theta}{\partial r}\\ \nabla u_{\theta \theta}&=\frac{\partial u_\theta}{r\partial \theta}+\frac{u_r}{r}\\ \nabla u_{\theta z}&=\frac{\partial u_\theta}{\partial z}\\ \nabla u_{z \theta}&=\frac{\partial u_z}{r\partial \theta}\\ \nabla u_{rz}&=\frac{\partial u_r}{\partial z}\\ \nabla u_{z r}&=\frac{\partial u_z}{\partial r}\\ \nabla u_{zz}&=\frac{\partial u_z}{\partial z} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7a6052edf8b96fc22643164918eb99ac_l3.png)
Therefore, ![]() has the following form:
has the following form:
![Rendered by QuickLaTeX.com \[ \nabla u'=\left(\begin{matrix} \frac{\partial u_r}{\partial r} & \frac{\partial u_r}{r\partial \theta}-\frac{u_{\theta}}{r} &\frac{\partial u_r}{\partial z}\\ \frac{\partial u_\theta}{\partial r} & \frac{\partial u_\theta}{r\partial \theta}+\frac{u_r}{r} &\frac{\partial u_\theta}{\partial z}\\ \frac{\partial u_z}{\partial r} & \frac{\partial u_z}{r\partial \theta}& \frac{\partial u_z}{\partial z} \end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8f4d8eda15111fb04039b9bf0b0c3bc4_l3.png)
Divergence of a Vector Field
If ![]() is given similar to the previous section, then, the divergence of
is given similar to the previous section, then, the divergence of ![]() in a cylindrical coordinate system is given by:
in a cylindrical coordinate system is given by:
![]()
Gradient of a Tensor Field
Let ![]() be a tensor field with components
be a tensor field with components ![]() with
with ![]() . First, we use the tensor product representation of the tensor field to find the derivatives of
. First, we use the tensor product representation of the tensor field to find the derivatives of ![]() with respect to
with respect to ![]() , and
, and ![]() . The derivatives with respect to
. The derivatives with respect to ![]() and
and ![]() are straightforward since
are straightforward since ![]() , and
, and ![]() are independent of
are independent of ![]() and
and ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\partial T(r,\theta,z)}{\partial r}=&\frac{\partial T_{rr}}{\partial r}e_r\otimes e_r+\frac{\partial T_{r\theta}}{\partial r}e_r\otimes e_\theta+\frac{\partial T_{rz}}{\partial r}e_r\otimes e_z\\ & +\frac{\partial T_{\theta r}}{\partial r}e_\theta\otimes e_r+\frac{\partial T_{\theta\theta}}{\partial r}e_\theta\otimes e_\theta+\frac{\partial T_{\theta z}}{\partial r}e_\theta\otimes e_z\\ & +\frac{\partial T_{zr}}{\partial r}e_z\otimes e_r+\frac{\partial T_{z\theta}}{\partial r}e_z\otimes e_\theta+\frac{\partial T_{zz}}{\partial r}e_z\otimes e_z \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b93d9ef5dd6f4088eb6ab2c54b40cb3f_l3.png)
Similarly,
![Rendered by QuickLaTeX.com \[\begin{split} \frac{\partial T(r,\theta,z)}{\partial z}=&\frac{\partial T_{rr}}{\partial z}e_r\otimes e_r+\frac{\partial T_{r\theta}}{\partial z}e_r\otimes e_\theta+\frac{\partial T_{rz}}{\partial z}e_r\otimes e_z\\ & +\frac{\partial T_{\theta r}}{\partial z}e_\theta\otimes e_r+\frac{\partial T_{\theta\theta}}{\partial z}e_\theta\otimes e_\theta+\frac{\partial T_{\theta z}}{\partial z}e_\theta\otimes e_z\\ & +\frac{\partial T_{zr}}{\partial z}e_z\otimes e_r+\frac{\partial T_{z\theta}}{\partial z}e_z\otimes e_\theta+\frac{\partial T_{zz}}{\partial z}e_z\otimes e_z \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2ebc0859b11796ac0c5ed47aee24ee22_l3.png)
However, the dependence of ![]() and
and ![]() on
on ![]() leads to the following derivative of
leads to the following derivative of ![]() with respect to
with respect to ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{\partial T(r,\theta,z)}{\partial \theta}=&\frac{\partial T_{rr}}{\partial \theta}e_r\otimes e_r+\frac{\partial T_{r\theta}}{\partial \theta}e_r\otimes e_\theta+\frac{\partial T_{rz}}{\partial \theta}e_r\otimes e_z\\ & +\frac{\partial T_{\theta r}}{\partial \theta}e_\theta\otimes e_r+\frac{\partial T_{\theta\theta}}{\partial \theta}e_\theta\otimes e_\theta+\frac{\partial T_{\theta z}}{\partial \theta}e_\theta\otimes e_z\\ & +\frac{\partial T_{zr}}{\partial \theta}e_z\otimes e_r+\frac{\partial T_{z\theta}}{\partial \theta}e_z\otimes e_\theta+\frac{\partial T_{zz}}{\partial \theta}e_z\otimes e_z\\ &+T_{rr}e_r\otimes e_\theta+T_{rr}e_\theta\otimes e_r-T_{r\theta}e_r\otimes e_r+T_{r\theta}e_\theta\otimes e_\theta+T_{rz}e_\theta\otimes e_z\\ &+T_{\theta r}e_\theta\otimes e_\theta-T_{\theta r}e_r\otimes e_r-T_{\theta\theta}e_\theta\otimes e_r-T_{\theta\theta}e_r\otimes e_\theta-T_{\theta z}e_r\otimes e_z\\ &+T_{z r}e_z\otimes e_\theta-T_{z\theta}e_z\otimes e_r \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-67f768becb272af6c926b4d33fea6a11_l3.png)
Using the general definition of the gradient of a tensor field, the components of the gradient of ![]() denoted by
denoted by ![]() in the cylindrical coordinate system can be obtained in a manner similar to the previous section. Let the components be
in the cylindrical coordinate system can be obtained in a manner similar to the previous section. Let the components be ![]() with
with ![]() . Then, it is straightforward (but with lots of details) to show that when
. Then, it is straightforward (but with lots of details) to show that when ![]() or
or ![]() :
:
![]()
Therefore:
![Rendered by QuickLaTeX.com \[\begin{split} (\nabla T)_{\alpha\beta r}=&\frac{\partial T_{\alpha \beta}}{\partial r}\\ (\nabla T)_{\alpha\beta z}=&\frac{\partial T_{\alpha \beta}}{\partial z} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fba8e649362f9965b77e8f8a2192a89c_l3.png)
However, the components when \gamma=\theta have the following form:
![Rendered by QuickLaTeX.com \[ \begin{split} (\nabla T)_{rr\theta}=&\frac{\partial T_{rr}}{r\partial \theta}-\frac{T_{r\theta}}{r}-\frac{T_{\theta r}}{r}\\ (\nabla T)_{r\theta\theta}=&\frac{\partial T_{r\theta}}{r\partial \theta}+\frac{T_{rr}}{r}-\frac{T_{\theta \theta}}{r}\\ (\nabla T)_{rz\theta}=&\frac{\partial T_{rz}}{r\partial \theta}-\frac{T_{\theta z}}{r}\\ (\nabla T)_{\theta r\theta}=&\frac{\partial T_{\theta r}}{r\partial \theta}+\frac{T_{rr}}{r}-\frac{T_{\theta \theta}}{r}\\ (\nabla T)_{\theta \theta \theta}=&\frac{\partial T_{\theta \theta}}{r\partial \theta}+\frac{T_{r\theta}}{r}+\frac{T_{\theta r}}{r}\\ (\nabla T)_{\theta z\theta}=&\frac{\partial T_{\theta z}}{r\partial \theta}+\frac{T_{rz}}{r}\\ (\nabla T)_{zr\theta}=&\frac{\partial T_{zr}}{r\partial \theta}-\frac{T_{z\theta}}{r}\\ (\nabla T)_{z \theta \theta}=&\frac{\partial T_{z\theta}}{r\partial \theta}+\frac{T_{zr}}{r}\\ (\nabla T)_{zz\theta}=&\frac{\partial T_{zz}}{r\partial \theta}\\ \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cbb2c2ab3cade36c342674258c6ff0d2_l3.png)
Divergence of a Tensor Field
Let ![]() be a tensor field with the cylindrical coordinate system components
be a tensor field with the cylindrical coordinate system components ![]() with
with ![]() .
.
Using the general definition of the divergence of a tensor field, the components of \mathrm{div}{(T)} in a cylindrical coordinate system can be obtained as follows:
![Rendered by QuickLaTeX.com \[\begin{split} (\mathrm{div}(T))_r=&\mathrm{div}(Te_r)=\mathrm{Trace}(\nabla T e_r)\\ (\mathrm{div}(T))_\theta=&\mathrm{div}(Te_\theta)=\mathrm{Trace}(\nabla T e_\theta)\\ (\mathrm{div}(T))_z=&\mathrm{div}(Te_z)=\mathrm{Trace}(\nabla T e_z) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-881f042732597803e6a8ca8b8ad7872f_l3.png)
where ![]() , and
, and ![]() are fixed in space at a particular point. I.e., the
are fixed in space at a particular point. I.e., the ![]() operator only applies to
operator only applies to ![]() . The procedure used in the gradient of a vector in a cylindrical coordinate system section combined with the derivatives of
. The procedure used in the gradient of a vector in a cylindrical coordinate system section combined with the derivatives of ![]() shown in the previous section can be used to reach the following formulas for the components of the divergence of
shown in the previous section can be used to reach the following formulas for the components of the divergence of ![]() in a cylindrical coordinate system:
in a cylindrical coordinate system:
![Rendered by QuickLaTeX.com \[\begin{split} \mathrm{div}{(T)}&=\left(\begin{array}{c} \mathrm{Trace}(\nabla Te_r)\\\mathrm{Trace}(\nabla Te_\theta)\\\mathrm{Trace}(\nabla Te_z)\end{array}\right)\\ &=\left(\begin{array}{c} \left(\frac{\partial T}{\partial r}e_r \right)\cdot e_r + \left(\frac{\partial T}{r\partial \theta}e_r \right)\cdot e_\theta + \left(\frac{\partial T}{\partial z}e_r \right)\cdot e_z\\ \left(\frac{\partial T}{\partial r}e_\theta \right)\cdot e_r + \left(\frac{\partial T}{r\partial \theta}e_\theta \right)\cdot e_\theta + \left(\frac{\partial T}{\partial z}e_\theta \right)\cdot e_z\\ \left(\frac{\partial T}{\partial r}e_z \right)\cdot e_r + \left(\frac{\partial T}{r\partial \theta}e_z \right)\cdot e_\theta + \left(\frac{\partial T}{\partial z}e_z \right)\cdot e_z\end{array}\right)\\ &=\left(\begin{array}{c} \sum_{\alpha\in\{r,\theta,z\}}(\nabla T)_{\alpha r r}\\ \sum_{\alpha\in\{r,\theta,z\}}(\nabla T)_{\alpha \theta \theta} \\ \sum_{\alpha\in\{r,\theta,z\}}(\nabla T)_{\alpha z z}\end{array}\right) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-66d0ae47e588a09de799b5991ea525c1_l3.png)
Therefore:
![Rendered by QuickLaTeX.com \[ \mathrm{div}{(T)}=\left(\begin{array}{c} \frac{\partial T_{rr}}{\partial r}+\frac{\partial T_{r\theta}}{r\partial \theta}+\frac{T_{rr}-T_{\theta\theta}}{r}+\frac{\partial T_{rz}}{\partial z}\\ \frac{\partial T_{\theta r}}{\partial r}+\frac{\partial T_{\theta\theta}}{r\partial \theta}+\frac{T_{r\theta}+T_{\theta r}}{r}+\frac{\partial T_{\theta z}}{\partial z}\\ \frac{\partial T_{zr}}{\partial r}+\frac{\partial T_{z\theta}}{r\partial \theta}+\frac{T_{zr}}{r}+\frac{\partial T_{z z}}{\partial z} \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-63a2048c797e10677bd3c914fb3a6235_l3.png)
Curl of a Vector Field
Using the general definition of the Curl, if ![]() is a vector field given in terms of
is a vector field given in terms of ![]() , and
, and ![]() and represented in a cylindrical coodrinate system, then, the components of the curl of
and represented in a cylindrical coodrinate system, then, the components of the curl of ![]() are given by:
are given by:
![Rendered by QuickLaTeX.com \[\begin{split} (\mbox{curl}(u))_r&=(\mbox{curl}(u))\cdot e_r=\mbox{div}(u\times e_r)=\mbox{Trace}(\nabla u\times e_r)\\ (\mbox{curl}(u))_\theta&=(\mbox{curl}(u))\cdot e_\theta=\mbox{div}(u\times e_\theta)=\mbox{Trace}(\nabla u\times e_\theta)\\ (\mbox{curl}(u))_z&=(\mbox{curl}(u))\cdot e_z=\mbox{div}(u\times e_z)=\mbox{Trace}(\nabla u\times e_z) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7f2c507eee0d1d65e2b9029add60ea03_l3.png)
with the \nabla operator applied to u and not to the vectors ![]() , and
, and ![]() . Therefore in a cylindrical coordinate system:
. Therefore in a cylindrical coordinate system:
![Rendered by QuickLaTeX.com \[ \mbox{curl}(u)=\left(\begin{array}{c}\frac{\partial u_z}{r\partial \theta}-\frac{\partial u_{\theta}}{\partial z}\\ \frac{\partial u_r}{\partial z}-\frac{\partial u_z}{\partial r}\\ \frac{\partial u_\theta}{\partial r}+\frac{u_{\theta}}{r}-\frac{\partial u_r}{r\partial \theta} \end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-de3e4441cc332d7b32bfb97e17905b2c_l3.png)
Laplacian of a Scalar Field
Using the general definition of the Laplacian, if ![]() is a scalar function given in terms of
is a scalar function given in terms of ![]() , and
, and ![]() , then, the Laplacian of
, then, the Laplacian of ![]() is given by:
is given by:
![Rendered by QuickLaTeX.com \[\begin{split} \nabla^2\phi&=\mathrm{div}(\nabla \phi)\\ &=\mathrm{div}\left(\frac{\partial \phi}{\partial r} e_r + \frac{\partial \phi}{r\partial \theta} e_\theta+ \frac{\partial \phi}{\partial z} e_z\right)\\ &=\frac{\partial^2 \phi}{\partial r^2}+\frac{\partial^2 \phi}{r^2\partial \theta^2}+\frac{\partial \phi}{r\partial r}+\frac{\partial^2 \phi}{\partial z^2} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-edd4cc68fd2006398f15c06424624a79_l3.png)
Example
Let ![]() be given by
be given by ![]() . Find the gradient of
. Find the gradient of ![]() in the current coordinate system. Find the expression for
in the current coordinate system. Find the expression for ![]() and the gradient of
and the gradient of ![]() in a polar coordinate system.
in a polar coordinate system.
SOLUTION
In the Cartesian coordinate system, the gradient of ![]() has the form:
has the form:
![]()
Note that ![]() and
and ![]() can be represented in the Cartesian coordinate system using
can be represented in the Cartesian coordinate system using ![]() and
and ![]() instead of
instead of ![]() and
and ![]() as follows:
as follows:
![Rendered by QuickLaTeX.com \[ \begin{split} u=&\left(\begin{array}{c}r^2\\r^2\cos(\theta)\sin(\theta)\end{array}\right)\\ \nabla u=&\left(\begin{matrix}2r\cos(\theta)&2r\sin(\theta)\\r\sin(\theta)&r\cos(\theta)\end{matrix}\right) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-187fb00107a578ebd411b7bd7c45c0bb_l3.png)
It is important to note that this is a mere change of variables, but the components of ![]() and
and ![]() are still represented using the Cartesian coordinate system. The values themselves are just obtained using
are still represented using the Cartesian coordinate system. The values themselves are just obtained using ![]() and
and ![]() , rather than
, rather than ![]() and
and ![]() .
.
If ![]() , and
, and ![]() are the basis vectors in the Cartesian coordinate system, and if
are the basis vectors in the Cartesian coordinate system, and if ![]() and
and ![]() are the basis vectors in the cylindrical coordinate system, then the matrix of transformation from the Cartesian to the cylindrical coordinate system at a particular point depends on the value of theta at that particular point and is given by:
are the basis vectors in the cylindrical coordinate system, then the matrix of transformation from the Cartesian to the cylindrical coordinate system at a particular point depends on the value of theta at that particular point and is given by:
![]()
If ![]() is the expression of
is the expression of ![]() in the polar coordinate system, it has the form:
in the polar coordinate system, it has the form:
![]()
The representation ![]() in the cylindrical coordinate system can be obtained using the change of coordinates formula:
in the cylindrical coordinate system can be obtained using the change of coordinates formula:
![]()
Alternatively, the gradient of u in the cylindrical coordinate system can be obtained directly using the components ![]() and
and ![]() :
:
![]()
Noting that ![]() , the two methods produce identical results for the components of the gradient in the polar coordinate system.
, the two methods produce identical results for the components of the gradient in the polar coordinate system.
The following figure shows the directions at an arbitrary point ![]() in a Cartesian coordinate system (left) and the representation of
in a Cartesian coordinate system (left) and the representation of ![]() and
and ![]() in that coordinate system. On the right, the polar coordinate system directions are shown along with the representation
in that coordinate system. On the right, the polar coordinate system directions are shown along with the representation ![]() and
and ![]() .
.
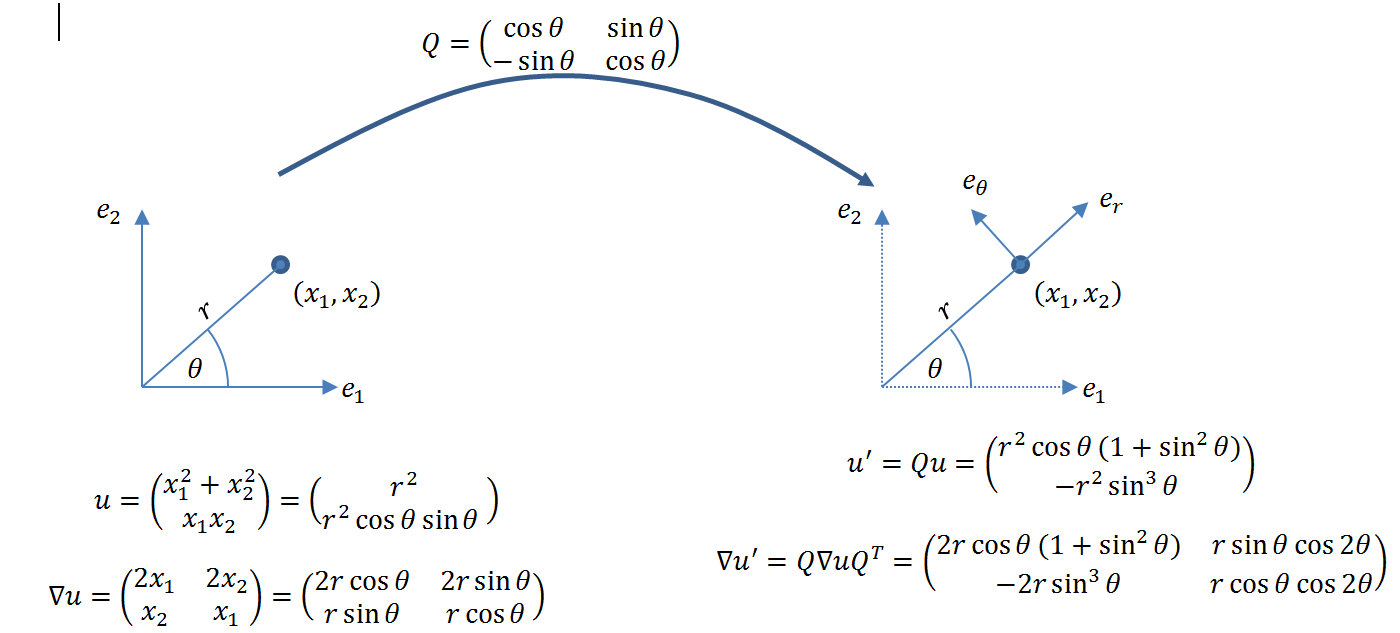
View Mathematica Code
Q={{Cos[th],Sin[th]},{-Sin[th],Cos[th]}};
u={x1^2+x2^2,x1*x2};
x={x1,x2}
rule={x1->r*Cos[th],x2->r*Sin[th]}
urth=FullSimplify[u/.rule]
Gu=Table[D[u[[i]],x[[j]]],{i,1,2},{j,1,2}]
Gurth=FullSimplify[Gu/.rule]
up=FullSimplify[Q.urth]
Gup=FullSimplify[Q.Gurth.Transpose[Q]]
Gup//MatrixForm
Guformula=FullSimplify[{{D[up[[1]],r],D[up[[1]],th]/r-up[[2]]/r},{D[up[[2]],r],up[[1]]/r+D[up[[2]],th]/r}}];
Guformula//MatrixForm
FullSimplify[Guformula-Gup]
View Python Code
import sympy as sp
from sympy import diff, simplify
from sympy.matrices import Matrix
sp.init_printing(use_latex = "mathjax")
x1,x2 = sp.symbols('x_1 x_2')
r, theta = sp.symbols('r \u03B8')
u1 = x1**2+x2**2
u2 = x1*x2
# cartesian coordinate system
u = Matrix([u1,u2])
display("u =",u)
x=Matrix([x1,x2])
# gradient
grad_u=Matrix([[diff(ui,xj) for xj in x] for ui in u])
display("\u2207u =",grad_u)
# Change of variables
display("The following is a simple change of variables but the components are still in the cartesian coordinate system")
urth = u.subs([(x1, r*sp.cos(theta)), (x2, r*sp.sin(theta))])
display("u_r_\u03B8 =",urth,simplify(urth))
# gradient
grad_u_rth = grad_u.subs([(x1, r*sp.cos(theta)), (x2, r*sp.sin(theta))])
display("\u2207u_r_\u03B8 =",grad_u_rth)
# rot matrix
Q = Matrix([[sp.cos(theta),sp.sin(theta)],[-sp.sin(theta),sp.cos(theta)]])
display("Q =",Q)
# Change of coordinates
display("The following representation is in the radial coordinate system")
upolar=simplify(Q*urth)
grad_u_polar=simplify(Q*grad_u_rth*Q.T)
display("u' = Q*u =",upolar)
display("\u2207u' = Q*\u2207u*Q^T =",grad_u_polar)
# Gradient formula in the polar coordinate system
display("The gradient can also be calculated using the gradient formula")
grad_u_formula=Matrix([[diff(upolar[0],r),diff(upolar[0],theta)/r-upolar[1]/r],
[diff(upolar[1],r),upolar[0]/r+diff(upolar[1],theta)/r]])
grad_u_formula=simplify(grad_u_formula)
display(grad_u_formula)
