Open Educational Resources

Energy: Strain Energy in a Continuum

During the time period of application of the external forces on a deforming body, the external forces perform work that is transmitted into internal energy inside the deforming body. To accurately describe this internal energy stored, the power of those external forces (rate of application of work) is used and then integrated over a small period of time to find the increment of the deformation energy stored inside the body. This concept will be used in the following sections to show that the increment in the deformation energy stored in a continuum arises naturally from the product of the components of the stress tensor and the components of the increments in the small strain tensor:

    \[ \mathrm{d}\overline{U}=\sum_{i,j=1}^3\sigma_{ij}\mathrm{d}\varepsilon_{ij} \]

Deformation Energy of a Continuum-Integral Formulation:

There are different approaches to find the expression for the deformation energy of a continuum. I prefer to start with the equilibrium equation and integrate it over the region of interest. This approach is similar to how the energy was defined in the single degree of freedom page. First, let the current configuration of a material body be represented by the set \Omega\in\mathbb{R}^3 with the orthonormal basis set B=\{e_1,e_2,e_3\} such that \forall x\in\Omega:x has coordinates x_1, x_2, and x_3. Let \Omega_{0}\in\mathbb{R}^3 be the reference configuration such that an arbitrary element of \Omega_{0} is denoted by X with coordinates X_1, X_2, and X_3. Integrals of a function f(x) over \Omega take the following form:

    \[ \int_{\Omega} \! f(x) \, \mathrm{d}x \]

while integrals of a function g(X) over \Omega_{0} take the following form:

    \[ \int_{\Omega_0} \! g(X) \, \mathrm{d}X \]

If F is the deformation gradient, then, integrals over \Omega can be converted to integrals over \Omega_{0} by utilizing the equality \mathrm{d}x=J\mathrm{d}X where J=\det{F}:

    \[ \int_{\Omega} \! f(x) \, \mathrm{d}x=\int_{\Omega_0} \! f(x(X))J \, \mathrm{d}X \]

Also, let \sigma(x)\in\mathbb{M}^3 be the Cauchy stress tensor map at every point and v(x),a(x)\in\mathbb{R}^3 be the velocity and acceleration maps, respectively, at each material point inside the deforming body. Let the vector map of the body forces acting on the continuum body be represented by b(x)\in\mathbb{R}^3 and the density map be denoted by \rho(x)\in\mathbb{R}. We first note that the equilibrium equation (balance of linear momentum) can be applied at any point in the continuum and at any point in time, i.e., \forall x\in\Omega, \forall t, \forall i\in{1,2,3}:

    \[ \rho a_i-\sum_{j=1}^3\frac{\partial \sigma_{ji}}{\partial x_j}-\rho b_i=0 \]

Or in vector form:

    \[ \rho a - \mathrm{div}\sigma - \rho b=0 \]

The dot product between the three components of the equilibrium equation and the velocity vector is equal to zero:

    \[ \sum_{i=1}^3\left(\rho a_i-\sum_{j=1}^3\frac{\partial \sigma_{ji}}{\partial x_j}-\rho b_i\right)v_i=0 \]

or in vector form:

    \[ \left(\rho a - \mathrm{div}\sigma - \rho b\right)\cdot v=0 \]

Since this applies to every x, the integral of this quantity over \Omega is still equal to zero:

(1)   \begin{equation*} \int_{\Omega} \! \left(\rho a - \mathrm{div}\sigma - \rho b\right)\cdot v \, \mathrm{d}x=0 \end{equation*}

The second term in Equation 1 can further manipulated using components as follows:

    \[ \begin{split} \int_{\Omega} \! \mathrm{div}\sigma\cdot v \, \mathrm{d}x & = \int_{\Omega} \! \sum_{i,j=1}^3\frac{\partial \sigma_{ji}}{\partial x_j}v_i \, \mathrm{d}x =\int_{\Omega} \! \sum_{i,j=1}^3\frac{\partial \sigma_{ji}v_i}{\partial x_j}-\sigma_{ji}\frac{\partial v_i}{\partial x_j} \, \mathrm{d}x\\ & = \int_{\partial \Omega} \! \sum_{i,j=1}^3 \sigma_{ji}v_in_j \mathrm{d}s-\sigma_{ji}\frac{\partial v_i}{\partial x_j} \, \mathrm{d}x\\ & = \int_{\partial \Omega} \! t_n \cdot v \mathrm{d}s- \int_{\Omega} \! \mathrm{Trace}(\sigma L) \mathrm{d}x \end{split} \]

where the equality t_n=\sigma^T n=\sigma n and the divergence theorem were used, and L is the velocity gradient. Substituting back into Equation 1 yields the following:

(2)   \begin{equation*} \int_{\Omega} \! \rho a \cdot v \, \mathrm{d}x + \int_{\Omega} \! \mathrm{Trace}(\sigma L) \, \mathrm{d}x= \int_{\Omega} \! \rho b\cdot v \, \mathrm{d}x + \int_{\partial \Omega} \! t_n\cdot v \, \mathrm{d}s \end{equation*}

The right hand side of Equation 2 gives the total external power (energy per unit time) supplied by the external body forces (\rho b) and external forces (t_n) acting on the boundary. The first term on the left hand side will be shown to be equal to the rate of change in the kinetic energy of \Omega as follows: The kinetic energy is defined as:

    \[ KE=\int_{\Omega} \! \frac{\rho}{2} v \cdot v \, \mathrm{d}x \]

The rate of change of the kinetic energy can be calculated as follows:

    \[ \begin{split} \frac{\mathrm{d}KE}{\mathrm{d}t} & =\frac{\mathrm{d}}{\mathrm{d}t}\int_{\Omega} \! \frac{\rho}{2} v \cdot v \, \mathrm{d}x\\ & = \frac{\mathrm{d}}{\mathrm{d}t}\int_{\Omega_0} \! \frac{\rho J}{2} v \cdot v \, \mathrm{d}X \\ & = \int_{\Omega_0} \! \frac{1}{2}\frac{\mathrm{d}\rho J}{\mathrm{d}t} v \cdot v \, \mathrm{d}X+\int_{\Omega} \! \rho a \cdot v \, \mathrm{d}x \\ & = \int_{\Omega} \! \rho a \cdot v \, \mathrm{d}x \end{split} \]

where the mass balance equation \frac{\mathrm{d}\rho J}{\mathrm{d}t}=0 was used. Substituting back into Equation 2 yields:

    \[ \frac{\mathrm{d}KE}{\mathrm{d}t}+\int_{\Omega} \! \mathrm{Trace}(\sigma L) \, \mathrm{d}x = \mbox{External Power} \]

By invoking the first law of thermodynamics and by assuming the loading is isothermic (temperature is constant), then, the external power supplied to \Omega is equal to the rate of change of the kinetic energy and the internal energy. Denoting the internal energy per unit volume by \overline{U}, then, the rate of change of the internal energy per unit volume of \Omega is given by:

    \[ \dot{\overline{U}}=\mathrm{Trace}(\sigma L) \]

The term \mathrm{Trace}(\sigma L) is often referred to as the “stress power”. Because of the symmetry of \sigma, we can replace L with its symmetric part D so that we have:

    \[ \dot{\overline{U}}=\mathrm{Trace}(\sigma D) \]

D is related to the small strain tensor as follows:

    \[ D_{ij}\mathrm{d}t=\frac{1}{2}\left(\frac{\partial v_i\mathrm{d}t}{\partial x_j}+\frac{\partial v_j\mathrm{d}t}{\partial x_i}\right)=\frac{1}{2}\left(\frac{\partial \mathrm{d}u_i}{\partial x_j}+\frac{\partial \mathrm{d}u_j}{\partial x_i}\right)=\mathrm{d}\varepsilon_{ij} \]

Therefore, the infinitesimal change in the internal energy can be calculated using the formula:

    \[ \mathrm{d}\overline{U}=\mathrm{Trace}(\sigma \mathrm{d}\varepsilon)=\sum_{i,j=1}^3\sigma_{ij}\mathrm{d}\varepsilon_{ij} \]

It is worth mentioning here that there was no need to invoke the “first law of thermodynamics” which is more useful in cases where sources of energy other than mechanical work are present. The argument that the power supplied by the external forces is equal to the rate of change of the kinetic energy plus the stress power in an isothermic process is equivalent to the equilibrium equation as it was directly derived from equilibrium.

Energy Conjugates:

The internal energy per unit volume is calculated by multiplying a measure of stress by a measure of deformation. If the energy per unit volume of the deformed configuration \Omega is considered, then the Cauchy stress matrix and the stretch part D of the velocity gradient are energy conjugates. If the energy per unit volume (W) of the undeformed configuration \Omega_0 is considered, then the first Piola Kirchoff stress P=J\sigma F^{-T} and the deformation gradient are energy conjugates as follows:

    \[ \dot{W}=J\dot{\overline{U}}=J \mathrm{Trace}(\sigma L)=J \mathrm{Trace}(L \sigma)=J \mathrm{Trace}(\frac{1}{J}\dot{F}F^{-1}FP^T)=\mathrm{Trace}(\dot{F}P^T)=\sum_{i,j=1}^3 P_{ij}\dot{F}_{ij} \]

If we consider the second Piola Kirchhoff stress tensor S=F^{-1}P then either C=F^TF or \varepsilon_{Green}=\frac{1}{2}(C-I) can be considered as its energy conjugate:

    \[\begin{split} \dot{W} & =\mathrm{Trace}(\dot{F}P^T)=\mathrm{Trace}(P\dot{F}^T)=\mathrm{Trace}(FS\dot{F}^T)\\ & =\frac{1}{2}\left(\mathrm{Trace}(S\dot{F}^TF) + \mathrm{Trace}(SF^T\dot{F})\right)\\ & = \frac{1}{2}\mathrm{Trace}(S\dot{C}) \\ & = \mathrm{Trace}(S\dot{\varepsilon}_{Green}) \\ \end{split} \]

Where the properties of the Trace operator were used along with the symmetry of S and C.
It is also important to note that since \nabla u=F-I, \nabla u can also be considered as the energy conjugate of P. I.e.,

    \[ \mathrm{d}W= P_{ij} \, \mathrm{d}F_{ij}= P_{ij} \, \mathrm{d}\nabla u_{ij} \]

If we integrate from state a to state b, and since the volume in the reference configuration is constant, we have:

    \[ W=\int_{F_a}^{F_b} \! P_{ij} \, \mathrm{d}F_{ij}=\int_{F_a}^{F_b} \! P_{ij} \, \mathrm{d}\nabla u_{ij} \]

Similarly, either of L=\frac{\partial v}{\partial x} or D=\frac{1}{2}\left(\frac{\partial v}{\partial x}+\frac{\partial v}{\partial x}^T\right) can be considered as the energy conjugate of \sigma. We can see the analogy between the conjugates of P and \sigma if we denote:

    \[ \nabla_x u =\frac{\partial u}{\partial x} \]

Then:

    \[ \mathrm{d}\overline{U}= \sigma_{ij} \, \mathrm{d}\nabla_x u_{ij} \]

In other words, the gradient of u in the reference configuration is the energy conjugate of P while the gradient of u in the spatial configuration is the energy conjugate of \sigma. To find the total energy using the spatial configuration expression for the energy per unit volume, the rate needs to be integrated over a particular volume, and then integrated from state a to state b:

    \[ \mbox{Total Energy}=\int_{a}^{b} \! \int_{\Omega} \! \dot{\overline{U}} \,\mathrm{d}x \, \mathrm{d}t \]

Illustrative Example 1: Rotation Followed by Extension

This example serves to clarify the difference between the various stress measures and strain measures studied before. In addition, the energy calculation as the product of components of stresses with the components of the “conjugate” strain measured will be shown. First, assume a block of material that whose length in the reference configuration is a, width is b, and thickness is c. Assume that the block rotates 90 degrees around the edge that is originally parallel to the axis X_3 as shown below. Then, a vertical load f is applied gradually on the block such that it changes linearly from 0 to f_0 during a time period t=1 units. Assume that the block deforms linearly with time such that a becomes a+\Delta a, b becomes b-\Delta b, and c becomes c-\Delta c. Let \varepsilon_a=\frac{\Delta a}{a}, \varepsilon_b=\frac{\Delta b}{b}, and \varepsilon_c=\frac{\Delta c}{c}. The following are the various stress and deformation measures describing the deformation.

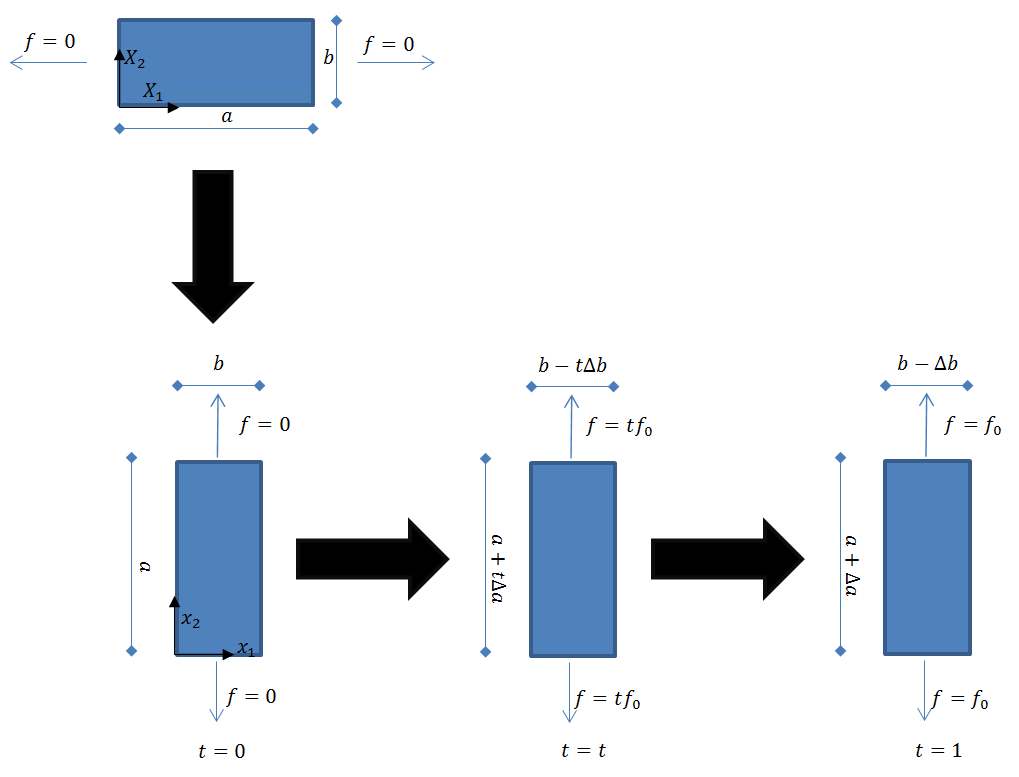
The Deformation Gradient

The 90 degrees rotation can be described by the following matrix:

    \[ Q=\left(\begin{matrix}\cos{\frac{\pi}{2}}&\sin{\frac{\pi}{2}}&0\\-\sin{\frac{\pi}{2}}&\cos{\frac{\pi}{2}}&0\\0&0&1\end{matrix}\right)=\left(\begin{matrix}0&1&0\\-1&0&0\\0&0&1\end{matrix}\right) \]

The deformation can be viewed as an extension along the direction a and contractions along the directions b and c followed by the rotation Q. The extension and contractions can be described by the matrix U:

    \[ U=\left(\begin{matrix}(1+t\varepsilon_a)&0&0\\0&(1-t\varepsilon_b)&0\\0&0&(1-t\varepsilon_c)\end{matrix}\right) \]

Therefore, the deformation gradient is given by:

    \[ F=QU=\left(\begin{matrix}0&(1-t\varepsilon_b)&0\\(-1-t\varepsilon_a)&0&0\\0&0&(1-t\varepsilon_c)\end{matrix}\right) \]

Note that QU is the right polar decomposition of F. Alternatively, the deformation can be viewed as a rotation Q followed by the same extensions and contractions which can be described by the matrix V:

    \[ V=\left(\begin{matrix}(1-t\varepsilon_b)&0&0\\0&(1+t\varepsilon_a)&0\\0&0&(1-t\varepsilon_c)\end{matrix}\right) \]

In this case, F=VQ. Notice how the extension along a and the contraction along b exchanged positions between the matrices U and V! The rate of the deformation gradient is given by:

    \[ \dot{F}=\left(\begin{matrix}0&-\varepsilon_b&0\\-\varepsilon_a&0&0\\0&0&-\varepsilon_c\end{matrix}\right) \]

The Velocity Gradient

The velocity gradient L is given by:

    \[ L=\dot{F}F^{-1}=\left(\begin{matrix}\frac{-\varepsilon_b}{1-t\varepsilon_b}&0&0\\0&\frac{\varepsilon_a}{1+t\varepsilon_a}&0\\0&0&\frac{-\varepsilon_c}{1-t\varepsilon_c}\end{matrix}\right) \]

As L is already symmetric, the stretch tensor is given by:

    \[ D=L=\left(\begin{matrix}\frac{-\varepsilon_b}{1-t\varepsilon_b}&0&0\\0&\frac{\varepsilon_a}{1+t\varepsilon_a}&0\\0&0&\frac{-\varepsilon_c}{1-t\varepsilon_c}\end{matrix}\right) \]

The spin tensor is given by:

    \[ W=0 \]

The Green-Lagrange Strain

The Green strain is given by:

    \[ \varepsilon_{\mbox{Green}}=\frac{1}{2}\left(F^TF-I\right)=\frac{1}{2}\left(U^2-I\right)=\left(\begin{matrix}t\varepsilon_a+\frac{t^2\varepsilon_a^2}{2}&0&0\\0&-t\varepsilon_b+\frac{t^2\varepsilon_b^2}{2}&0\\0&0&-t\varepsilon_c+\frac{t^2\varepsilon_c^2}{2}\end{matrix}\right) \]

Its rate is given by:

    \[ \dot{\varepsilon}_{\mbox{Green}}=\left(\begin{matrix}\varepsilon_a(1+t\varepsilon_a)&0&0\\0&-\varepsilon_b(1-t\varepsilon_b)&0\\0&0&-\varepsilon_c(1-t\varepsilon_c)\end{matrix}\right) \]

The Cauchy Stress Tensor

The Cauchy stress describes the spacial state of stress of the block. In the spacial coordinate system, the Cauchy stress matrix has only one non-zero component and thus at time 0\leq t \leq 1 has the form:

    \[ \sigma=\left(\begin{matrix}0&0&0\\0&\frac{tf_0}{bc(1-t\varepsilon_b)(1-t\varepsilon_c)}&0\\0&0&0\end{matrix}\right) \]

It is important first to note that unlike the load and the deformation are linear in time and thus proportional, the component \sigma_{22} is nonlinear. In fact, it has an increasing slope (i.e., it is convex). This can easily be shown by noting that the second derivative of \sigma_{22} with respect to t is always positive when 0\leq t\leq 1:

    \[ \frac{\mathrm{d}\sigma_{22}}{\mathrm{d}t}=\frac{f_0}{bc(1-t\varepsilon_b)^2(1-t\varepsilon_c)^2}\left(1-\varepsilon_b\varepsilon_c t^2\right) \]

Piola Kirchhoff Stress Tensors

The first Piola Kirchhoff stress tensor P is given by:

    \[ P=\det{(F)}\sigma^TF^{-T}=\left(\begin{matrix}0&0&0\\\frac{-tf_0}{bc}&0&0\\0&0&0\end{matrix}\right) \]

P is not symmetric. The first column gives the spatial components of the spatial force per unit undeformed area acting on the area perpendicular to the reference axis X_1.


The second Piola Kirchhoff stress tensor S is given by:

    \[ S=F^{-1}P=\left(\begin{matrix}\frac{tf_0}{bc(1+t\varepsilon_a)}&0&0\\0&0&0\\0&0&0\end{matrix}\right) \]

The first column gives the components in the reference configuration of the force vector acting on the area perpendicular to the reference axis X_1 when the force vector is pulled back to the reference configuration. Note that when the force vector is pulled back, it is now acting in the horizontal direction and is scaled down by the factor (1+t\varepsilon_a).

Energy Conjugates

First, the total strain energy due to deformation will be computed. The gradual increase in the force f causes a gradual increase in the length a to a+\Delta a. The force f as a function of time is given by tf_0 while the extension u is given by t\Delta a. The total strain energy can be calculated as follows:

    \[ \mbox{Total Energy}=\int_{a}^{a+\Delta a} \! f \, \mathrm{d}u=\int_{0}^1 \! f\dot{u} \, \mathrm{d}t=\int_{0}^1 \! tf_0\Delta a \, \mathrm{d}t=\frac{f_0\Delta a}{2} \]

The energy per unit volume of the undeformed configuration W can be obtained as follows:

    \[ W=\int_{0}^1 \! \frac{tf_0\Delta a}{abc} \, \mathrm{d}t=\int_{0}^{1} \! \frac{tf_0}{bc}\varepsilon_a \, \mathrm{d}t=\int_{0}^{1} \! P_{12}\dot{F}_{12} \, \mathrm{d}t \]

Alternatively:

    \[ W=\int_{0}^{1} \! \frac{tf_0}{bc(1+t\varepsilon_a)}((1+t\varepsilon_a)\varepsilon_a) \, \mathrm{d}t=\int_{0}^{1} \! S_{11}({\dot{\varepsilon}_{Green}})_{11} \, \mathrm{d}t \]

The above two expressions show that \dot{F}_{12} arises naturally as the energy conjugate of P_{12} while ({\dot{\varepsilon}_{Green}})_{11} arises naturally as the energy conjugate of S_{11}. The instantaneous change of energy per unit deformed configuration volume can be obtained as follows:

    \[ \dot{\overline{U}}= \frac{tf_0\Delta a}{abc(1+t\varepsilon_a)(1-t\varepsilon_b)(1-t\varepsilon_c)} =\sigma_{22}D_{22} \]

Similarly, D_{22} arises naturally as the energy conjugate of \sigma_{22}. It is important to note that the energy per unit deformed configuration volume can only be obtained by first integrating over a particular volume, then integrating over time, and then dividing by the total volume. Simple integration of \dot{\overline{U}} over time is not conceptually correct, since the volume changes with time.

View Mathematica Code

Q = {{Cos[Pi/2], Sin[Pi/2], 0}, {-Sin[Pi/2], Cos[Pi/2], 0}, {0, 0, 1}};
intx = {xi1, xi2, xi3};
X = {X1, X2, X3};
xi1 = (1 + t*ea) X1;
xi2 = (1 - t*eb) X2;
xi3 = (1 - t*ec) X3;
xi = {xi1, xi2, xi3};
x = Q.xi;
x // MatrixForm
x /. {t -> 1, X2 -> b, X1 -> a, X3 -> c} // MatrixForm
U = Table[D[xi[[i]], X[[j]]], {i, 1, 3}, {j, 1, 3}];
Print["The matrix U appearing in the Right Polar Decomposition of the \ Deformation Gradient F:"]
U // MatrixForm
Udot = D[U, t];
Udot // MatrixForm
Qdot = D[Q, t];
Qdot // MatrixForm
F = Table[D[x[[i]], X[[j]]], {i, 1, 3}, {j, 1, 3}];
Print["The Deformation Gradient F:"]
F // MatrixForm
Print["The matrix V appearing in the Right Polar Decomposition of the \ Deformation Gradient F:"]
V = FullSimplify[F.Transpose[Q]];
V // MatrixForm
Fdot = FullSimplify[D[F, t]];
Print["Fdot"]
Fdot // MatrixForm
L = FullSimplify[Fdot.Inverse[F]];
Print["Velocity gradient (L)"]
L // MatrixForm
Print["Velocity gradient (L) at t=0.5"]
FullSimplify[L /. t -> 0.5] // MatrixForm
Print["Velocity gradient (L) at t=1"]
FullSimplify[L /. t -> 1] // MatrixForm
Dd = FullSimplify[1/2 (L + Transpose[L])];
Print["Symmetric part of Velocity gradient"]
Dd // MatrixForm
Print["D at t=0.5"]
FullSimplify[Dd /. t -> 0.5] // MatrixForm
Print["D at t=1"]
FullSimplify[Dd /. t -> 1] // MatrixForm
Elagrange = FullSimplify[1/2 (Transpose[F].F - IdentityMatrix[3])]; Print["Green Strain"]
Elagrange // MatrixForm
Elagrangedot = FullSimplify[D[Elagrange, t]];
Print["Green Strain Rate"]
Elagrangedot // MatrixForm
sigmalocal = {{t*f0/(b*c*(1 - t*eb) (1 - t*ec)), 0, 0}, {0, 0, 0}, {0,0, 0}};
Cauchy = FullSimplify[Q.sigmalocal.Transpose[Q]];
Print["Cauchy stress"]
Cauchy // MatrixForm
sigmalocal /. t -> 0 // MatrixForm;
sigmalocal /. t -> 0.5 // MatrixForm;
sigmalocal /. t -> 1 // MatrixForm;
Print["Cauchy stress at t=0"]
Cauchy /. t -> 0 // MatrixForm
Print["Cauchy stress at t=0.5"]
Cauchy /. t -> 0.5 // MatrixForm
Print["Cauchy stress at t=1"]
Cauchy /. t -> 1 // MatrixForm
P = FullSimplify[Det[F]*Cauchy.Inverse[Transpose[F]]];
Print["P"]
P // MatrixForm
Print["P at t=0"]
P /. t -> 0 // MatrixForm
Print["P at t=0.5"]
P /. t -> 0.5 // MatrixForm
Print["P at t=1"]
P /. t -> 1 // MatrixForm
S = FullSimplify[Inverse[F].P];
Print["S"]
S // MatrixForm
Print["S at t=0"]
S /. t -> 0 // MatrixForm
Print["S at t=0.5"]
S /. t -> 0.5 // MatrixForm
Print["S at t=1"]
S /. t -> 1 // MatrixForm
Print["Cauchy"]
Cauchy // MatrixForm
Print["D"]
Dd // MatrixForm
Print["D and Cauchy are energy conjugates: dU/dt"]
e1 = FullSimplify[Sum[Cauchy[[i, j]]*Dd[[i, j]], {i, 1, 3}, {j, 1, 3}]]
Print["P"]
P // MatrixForm
Print["Fdot"]
Fdot // MatrixForm
Print["P and Fdot are energy conjugates: dW/dt"]
e2 = FullSimplify[Sum[P[[i, j]]*Fdot[[i, j]], {i, 1, 3}, {j, 1, 3}]]
Print["S"]
S // MatrixForm
Print["E-Green"]
Elagrangedot // MatrixForm
Print["S and E_Green are energy conugates: dW/dt"]
e2 = FullSimplify[Sum[S[[i, j]]*Elagrangedot[[i, j]], {i, 1, 3}, {j, 1, 3}]]

View Python Code

import sympy as sp
import numpy as np
from sympy import Matrix, simplify, diff, eye, det
from matplotlib import pyplot as plt
theta = sp.symbols("theta")
Q = Matrix([[sp.cos(theta), sp.sin(theta),0],
            [-sp.sin(theta),sp.cos(theta), 0],
            [0,0,1]])
Q = Q.subs({theta:sp.pi/2})
display("Q =", Q)
X1,X2,X3 = sp.symbols("X_1 X_2 X_3")
a,b,c = sp.symbols("a b c")
ea,eb,ec,t = sp.symbols("epsilon_a epsilon_b epsilon_c t")
f0 = sp.symbols("f_0")
xi1 = (1+t*ea)*X1
xi2 = (1-t*eb)*X2
xi3 = (1-t*ec)*X3
xi = Matrix([xi1, xi2, xi3])
x = Q*xi
X = Matrix([X1,X2,X3])
U = Matrix([[diff(i,j) for j in X] for i in xi])
display("Matrix U appearing in the Right polar decomposition of the deformation gradient F")
display("U =", U)
Udot = diff(U,t)
display("Udot =",Udot)
F = Matrix([[diff(i,j) for j in X] for i in x])
display("Deformation gradient F =",F)
V = F*Q.T
display("Matrix V appearing in the Right polar decomposition of the deformation gradient  F")
display("V =",V)
Fdot = diff(F,t)
display("Fdot =",Fdot)
L = Fdot*F.inv()
display("L =",L)
display("L @t=0.5 = ", L.subs({t:0.5}))
display("L @t=1 = ", L.subs({t:1}))
Dd = 1/2*(L+L.T)
display("Symmetric part of L", Dd)
Elagrange = 1/2*(F.T*F-eye(3))
display("Green Strain =",Elagrange)
Elagrangedot = diff(Elagrange,t)
display("Green Strain Rate =",Elagrangedot)
sigmalocal = Matrix([[t*f0/(b*c*(1-t*eb)*(1-t*ec)),0,0],[0,0,0],[0,0,0]])
Cauchy = Q*sigmalocal*Q.T
display("Cauchy stress =",Cauchy)
display("Cauchy stress @t=0:",Cauchy.subs({t:0}))
display("Cauchy stress @t=0.5:",Cauchy.subs({t:0.5}))
display("Cauchy stress @t=1:",Cauchy.subs({t:1}))
P = simplify(det(F)*Cauchy*F.T.inv())
display("P =",P)
display("P @ t=0",P.subs({t:0}))
display("P @ t=0.5",P.subs({t:0.5}))
display("P @ t=1",P.subs({t:1}))
S = F.inv()*P
display("S =",S)
display("S @ t=0",S.subs({t:0}))
display("S @ t=0.5",S.subs({t:0.5}))
display("S @ t=1",S.subs({t:1}))
# code is the same below
e1 = sum([sum([Cauchy[i,j]*Dd[i,j] for i in range(3)]) for j in range(3)])
#e1 = sum([Cauchy[i]*Dd[i] for i in range(9)])
e1 = sum([Cauchy[i]*Dd[i] for i in range(9)])
display("Cauchy",Cauchy,"Dd",Dd)
display("D and Cauchy are energy conjugates: dU/dt", e1)
e2 = sum([P[i]*Fdot[i] for i in range(9)])
display("P",P,"Fdot",Fdot)
display("P and Fdot are energy conjugates: dW/dt", e2)
e2 = sum([S[i]*Elagrangedot[i] for i in range(9)])
display("S",S,"E_Green",Elagrangedot)
display("S and E_Green are energy conjugates: dW/dt", e2)

Illustrative Example 2: Rotation Accompanied by Extension

Similar to the previous example, assume a block of material that whose length in the reference configuration is a, width is b, and thickness is c. Assume that the block rotates 90 degrees around the edge that is originally parallel to the axis X_3 as shown below while a vertical load f is applied gradually on the block such that it changes linearly from 0 to f_0 during a time period t=1 units. Assume that the block deforms linearly with time such that a becomes a+\Delta a, b becomes b-\Delta b, and c becomes c-\Delta c. Let \varepsilon_a=\frac{\Delta a}{a}, \varepsilon_b=\frac{\Delta b}{b}, and \varepsilon_c=\frac{\Delta c}{c}. The following are the various stress and deformation measures describing the deformation.

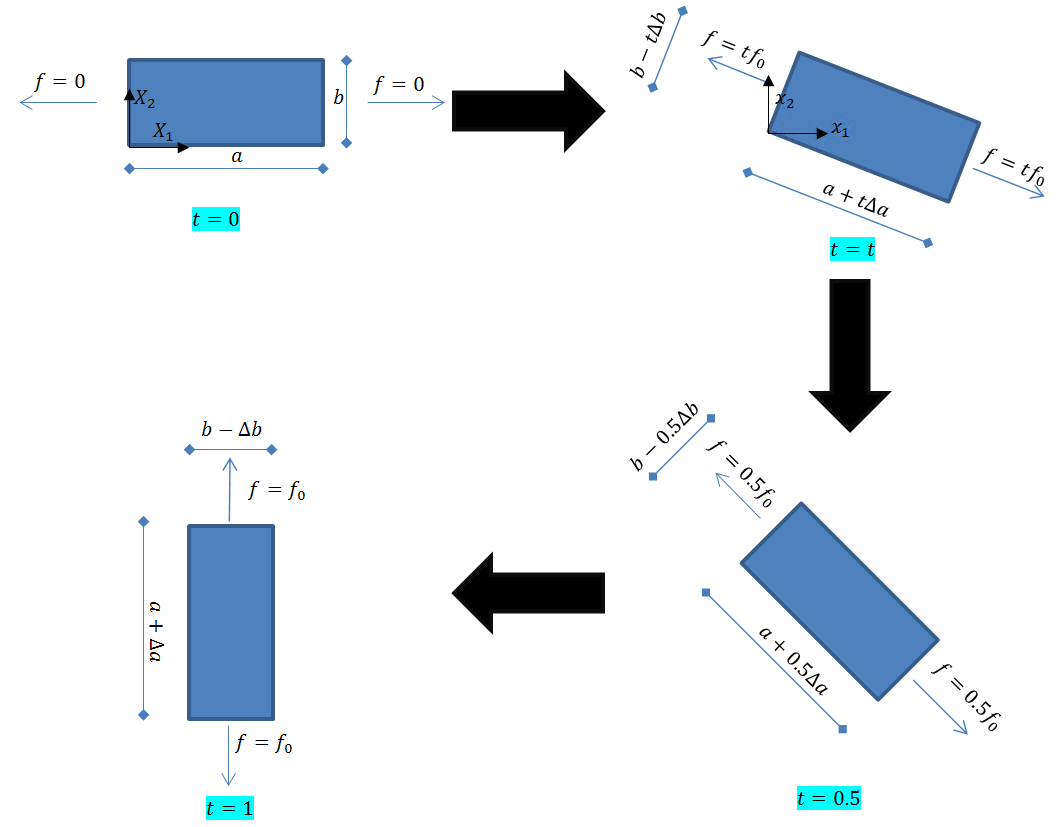
The Deformation Gradient

The 90 degrees rotation can be described by the following matrix:

    \[ Q=\left(\begin{matrix}\cos{\frac{t\pi}{2}}&\sin{\frac{t\pi}{2}}&0\\-\sin{\frac{t\pi}{2}}&\cos{\frac{t\pi}{2}}&0\\0&0&1\end{matrix}\right) \]

The deformation can be viewed as an extension along the direction a and contractions along the directions b and c followed by the rotation Q. The extension and contractions can be described by the matrix U:

    \[ U=\left(\begin{matrix}(1+t\varepsilon_a)&0&0\\0&(1-t\varepsilon_b)&0\\0&0&(1-t\varepsilon_c)\end{matrix}\right) \]

Therefore, the deformation gradient is given by:

    \[ F=QU=\left(\begin{matrix}(1+t\varepsilon_a)\cos{\frac{t\pi}{2}}&(1-t\varepsilon_b)\sin{\frac{t\pi}{2}}&0\\-(1+t\varepsilon_a)\sin{\frac{t\pi}{2}}&(1-t\varepsilon_b)\cos{\frac{t\pi}{2}}&0\\0&0&(1-t\varepsilon_c)\end{matrix}\right) \]

Note that QU is the right polar decomposition of F. Alternatively, the deformation can be viewed as a rotation Q followed by the same extensions and contractions in the corresponding directions which can be described by the matrix V:

    \[ V=FQ^T \]

The rate of the deformation gradient is given by:

    \[ \dot{F}=Q\dot{U}+\dot{Q}U \]

with

    \[ \dot{U}=\left(\begin{matrix}\varepsilon_a&0&0\\0&-\varepsilon_b&0\\0&0&-\varepsilon_c\end{matrix}\right) \]

and

    \[ \dot{Q}=\left(\begin{matrix}-\frac{\pi}{2}\sin{\frac{t\pi}{2}}&\frac{\pi}{2}\cos{\frac{t\pi}{2}}&0\\-\frac{\pi}{2}\cos{\frac{t\pi}{2}}&-\frac{\pi}{2}\sin{\frac{t\pi}{2}}&0\\0&0&0\end{matrix}\right) \]

The Velocity Gradient

The velocity gradient L is given by:

    \[ L=\dot{F}F^{-1}=\left(\begin{matrix}\frac{\varepsilon_b+\varepsilon_a(-1+2t\varepsilon_b)-(\varepsilon_a+\varepsilon_b)\cos{\pi t}}{2(1+t\varepsilon_a)(-1+t\varepsilon_b)}&\frac{\pi}{2}+\frac{(\varepsilon_a+\varepsilon_b)\sin{\pi t}}{2(1+t\varepsilon_a)(-1+t\varepsilon_b)}&0\\ \frac{-\pi}{2}+\frac{(\varepsilon_a+\varepsilon_b)\sin{\pi t}}{2(1+t\varepsilon_a)(-1+t\varepsilon_b)}&\frac{\varepsilon_b+\varepsilon_a(-1+2t\varepsilon_b)+(\varepsilon_a+\varepsilon_b)\cos{\pi t}}{2(1+t\varepsilon_a)(-1+t\varepsilon_b)}&0\\0&0&\frac{-\varepsilon_c}{1-t\varepsilon_c} \end{matrix}\right) \]

While its symmetric part D is given by:

    \[ D=\frac{1}{2}\left(L+L^T\right)=\left(\begin{matrix}\frac{\varepsilon_b+\varepsilon_a(-1+2t\varepsilon_b)-(\varepsilon_a+\varepsilon_b)\cos{\pi t}}{2(1+t\varepsilon_a)(-1+t\varepsilon_b)}&\frac{(\varepsilon_a+\varepsilon_b)\sin{\pi t}}{2(1+t\varepsilon_a)(-1+t\varepsilon_b)}&0\\ \frac{(\varepsilon_a+\varepsilon_b)\sin{\pi t}}{2(1+t\varepsilon_a)(-1+t\varepsilon_b)}&\frac{\varepsilon_b+\varepsilon_a(-1+2t\varepsilon_b)+(\varepsilon_a+\varepsilon_b)\cos{\pi t}}{2(1+t\varepsilon_a)(-1+t\varepsilon_b)}&0\\0&0&\frac{-\varepsilon_c}{1-t\varepsilon_c} \end{matrix}\right) \]

The spin tensor is given by:

    \[ W=\frac{1}{2}\left(L-L^T\right)=\left(\begin{matrix}0&\frac{\pi}{2}&0\\ \frac{-\pi}{2}&0&0\\0&0&0 \end{matrix}\right) \]

THE GREEN-LAGRANGE STRAIN

The Green strain is given by:

    \[ \varepsilon_{\mbox{Green}}=\frac{1}{2}\left(F^TF-I\right)=\frac{1}{2}\left(U^2-I\right)=\left(\begin{matrix}t\varepsilon_a+\frac{t^2\varepsilon_a^2}{2}&0&0\\0&-t\varepsilon_b+\frac{t^2\varepsilon_b^2}{2}&0\\0&0&-t\varepsilon_c+\frac{t^2\varepsilon_c^2}{2}\end{matrix}\right) \]

Its rate is given by:

    \[ \dot{\varepsilon}_{\mbox{Green}}=\left(\begin{matrix}\varepsilon_a(1+t\varepsilon_a)&0&0\\0&-\varepsilon_b(1-t\varepsilon_b)&0\\0&0&-\varepsilon_c(1-t\varepsilon_c)\end{matrix}\right) \]

Note that the Green strain in this example is identical to the Green strain in the previous example! The Green strain gives the strains along the original directions (measured in the undeformed configuration) which are identical for both examples!

THE CAUCHY STRESS TENSOR

In a local coordinate system that is aligned with the main edges of the cube, the Cauchy stress tensor is given by:

    \[ \sigma_{\mbox{local}}=\left(\begin{matrix}\frac{tf_0}{bc(1-t\varepsilon_b)(1-t\varepsilon_c)}&0&0\\0&0&0\\0&0&0\end{matrix}\right) \]

Setting s=\frac{tf_0}{bc(1-t\varepsilon_b)(1-t\varepsilon_c)}, the Cauchy Stress Tensor in the spatial coordinate system is given by:

    \[ \sigma=Q\sigma_{\mbox{local}}Q^T=\left(\begin{matrix}s\cos^2{\frac{\pi t}{2}}&-\frac{s\sin{\pi t}}{2}&0\\-\frac{s\sin{\pi t}}{2}&s\sin^2{\frac{\pi t}{2}}&0\\0&0&0\end{matrix}\right) \]

THE PIOLA KIRCHHOFF STRESS TENSORS

The first Piola Kirchhoff stress tensor is given by:

    \[ P=\det{(F)}\sigma^TF^{-T}=\left(\begin{matrix}\frac{tf_0\cos{\frac{\pi t}{2}}}{bc}&0&0\\\frac{-tf_0\sin{\frac{\pi t}{2}}}{bc}&0&0\\0&0&0\end{matrix}\right) \]

The first row gives the inclined force (the force in the spatial configuration) per unit original area acting on the area in the undeformed configuration perpendicular to the axis X_1. The second Piola Kirchhoff stress tensor is given by:

    \[ S=F^{-1}P=\left(\begin{matrix}\frac{tf_0}{bc(1+t\varepsilon_a)}&0&0\\0&0&0\\0&0&0\end{matrix}\right) \]

The first column gives the components in the reference configuration of the force vector acting on the area perpendicular to the reference axis X_1 when the force vector is pulled back to the reference configuration. Note that when the force vector is pulled back, it is now acting in the horizontal direction and is scaled down by the factor (1+t\varepsilon_a). The second Piola Kirchhoff stress tensor is similar to the one obtained in the previous illustrative example!

Energy Conjugates

Similar to the previous illustrative example, the rotation is not accompanied by any strain energy. The extension on the other hand is accompanied by a strain energy component that is equal to:

    \[ \mbox{Total Energy}=\frac{f_0\Delta a}{2} \]

The energy per unit volume of the undeformed configuration is given by:

    \[ W=\frac{f_0\Delta a}{2abc} \]

The second Piola Kirchhoff stress tensor and the Green strain tensor are energy conjugates of each other. Indeed, W can be obtained by integrating the inner product of S and \dot{\varepsilon}_{\mbox{Green}}:

    \[ W=\int_{0}^{1} \! S_{11}(\dot{\varepsilon}_{\mbox{Green}})_{11} \, \mathrm{d}t=\int_0^1 \! \frac{tf_0\varepsilon_a}{bc} \, \mathrm{d}t=\int_0^1 \! \frac{tf_0\Delta_a}{abc} \, \mathrm{d}t=\frac{f_0\Delta a}{2abc} \]

Alternatively, the same result would be obtained if P and F are used instead as energy conjugates:

    \[ W=\int_0^1 \! P_{11}\dot{F}_{11}+P_{12}\dot{F}_{12} \, \mathrm{d}t=\frac{f_0\Delta a}{2abc} \]

The strain energy rate per unit volume of the deformed configuration can be obtained as the inner product of D and \sigma:

    \[ \dot{\overline{U}}= \sigma_{11}D_{11}+\sigma_{12}D_{12}+\sigma_{21}D_{21}+\sigma_{22}D_{22}=\frac{tf_0\Delta a}{abc(1+t\varepsilon_a)(1-t\varepsilon_b)(1-t\varepsilon_c)} \]

which is the same result as the previous example! This should not come as a surprise since the two applied load and extension for the two examples are identical.

View Mathematica Code

Q = {{Cos[Pi/2*t], Sin[Pi/2*t], 0}, {-Sin[Pi/2*t], Cos[Pi/2*t], 0}, {0, 0, 1}};
intx = {xi1, xi2, xi3};
X = {X1, X2, X3};
xi1 = (1 + t*ea) X1;
xi2 = (1 - t*eb) X2;
xi3 = (1 - t*ec) X3;
xi = {xi1, xi2, xi3};
x = Q.xi;
x // MatrixForm
x /. {t -> 1, X2 -> b, X1 -> a, X3 -> c} // MatrixForm
U = Table[D[xi[[i]], X[[j]]], {i, 1, 3}, {j, 1, 3}];
Print["The matrix U appearing in the Right Polar Decomposition of the \ Deformation Gradient F:"]
U // MatrixForm
Udot = D[U, t];
Print["Udot"]
Udot // MatrixForm
Print["Qdot"]
Qdot = D[Q, t];
Qdot // MatrixForm
F = Table[D[x[[i]], X[[j]]], {i, 1, 3}, {j, 1, 3}];
Print["The Deformation Gradient F:"]
F // MatrixForm
Print["The matrix V appearing in the Right Polar Decomposition of the \ Deformation Gradient F:"]
V = FullSimplify[F.Transpose[Q]];
V // MatrixForm
Fdot = FullSimplify[D[F, t]];
Print["Fdot"]
Fdot // MatrixForm
L = FullSimplify[Fdot.Inverse[F]];
Print["Velocity gradient (L)"]
L // MatrixForm
Print["Velocity gradient (L) at t=0.5"]
FullSimplify[L /. t -> 0.5] // MatrixForm
Print["Velocity gradient (L) at t=1"]
FullSimplify[L /. t -> 1] // MatrixForm
Dd = FullSimplify[1/2 (L + Transpose[L])];
Print["Symmetric part of Velocity gradient"]
Dd // MatrixForm
Print["D at t=0.5"]
FullSimplify[Dd /. t -> 0.5] // MatrixForm
Print["D at t=1"]
FullSimplify[Dd /. t -> 1] // MatrixForm
Elagrange = FullSimplify[1/2 (Transpose[F].F - IdentityMatrix[3])];
Print["Green Strain"]
Elagrange // MatrixForm
Elagrangedot = FullSimplify[D[Elagrange, t]];
Print["Green Strain Rate"]
Elagrangedot // MatrixForm
sigmalocal = {{t*f0/(b*c*(1 - t*eb) (1 - t*ec)), 0, 0}, {0, 0, 0}, {0, 0, 0}};
Cauchy = FullSimplify[Q.sigmalocal.Transpose[Q]];
Print["Cauchy stress"]
Cauchy // MatrixForm
sigmalocal /. t -> 0 // MatrixForm;
sigmalocal /. t -> 0.5 // MatrixForm;
sigmalocal /. t -> 1 // MatrixForm;
Print["Cauchy stress at t=0"]
Cauchy /. t -> 0 // MatrixForm
Print["Cauchy stress at t=0.5"]
Cauchy /. t -> 0.5 // MatrixForm
Print["Cauchy stress at t=1"]
Cauchy /. t -> 1 // MatrixForm
P = FullSimplify[Det[F]*Cauchy.Inverse[Transpose[F]]];
Print["P"]
P // MatrixForm
Print["P at t=0"]
P /. t -> 0 // MatrixForm
Print["P at t=0.5"]
P /. t -> 0.5 // MatrixForm
Print["P at t=1"]
P /. t -> 1 // MatrixForm
S = FullSimplify[Inverse[F].P];
Print["S"]
S // MatrixForm
Print["S at t=0"]
S /. t -> 0 // MatrixForm
Print["S at t=0.5"]
S /. t -> 0.5 // MatrixForm
Print["S at t=1"]
S /. t -> 1 // MatrixForm
Print["Cauchy"]
Cauchy // MatrixForm
Print["D"]
Dd // MatrixForm
Print["D and Cauchy are energy conjugates: dU/dt"]
e1 = FullSimplify[Sum[Cauchy[[i, j]]*Dd[[i, j]], {i, 1, 3}, {j, 1, 3}]] Print["P"]
P // MatrixForm
Print["Fdot"]
Fdot // MatrixForm
Print["P and Fdot are energy conjugates: dW/dt"]
e2 = FullSimplify[Sum[P[[i, j]]*Fdot[[i, j]], {i, 1, 3}, {j, 1, 3}]] Print["S"]
S // MatrixForm
Print["E-Green"]
Elagrangedot // MatrixForm
Print["S and E_Green are energy conugates: dW/dt"]
e2 = FullSimplify[ Sum[S[[i, j]]*Elagrangedot[[i, j]], {i, 1, 3}, {j, 1, 3}]]

View Python Code

import sympy as sp
import numpy as np
from sympy import Matrix, simplify, diff, eye, det
from matplotlib import pyplot as plt
theta = sp.symbols("theta")
X1,X2,X3 = sp.symbols("X_1 X_2 X_3")
a,b,c = sp.symbols("a b c")
ea,eb,ec,t = sp.symbols("epsilon_a epsilon_b epsilon_c t")
f0 = sp.symbols("f_0")
Q = Matrix([[sp.cos(theta*t), sp.sin(theta*t),0],
            [-sp.sin(theta*t),sp.cos(theta*t), 0],
            [0,0,1]])
Q = Q.subs({theta:sp.pi/2})
display("Q =", Q)
xi1 = (1+t*ea)*X1
xi2 = (1-t*eb)*X2
xi3 = (1-t*ec)*X3
xi = Matrix([xi1, xi2, xi3])
x = Q*xi
X = Matrix([X1,X2,X3])
U = Matrix([[diff(i,j) for j in X] for i in xi])
display("The matrix U appearing in the Right Polar Decomposition of the Deformation Gradient F:")
display("U =", U)
Udot = diff(U,t)
display("Udot =",Udot)
F = Matrix([[diff(i,j) for j in X] for i in x])
display("F =",F)
V = simplify(F*Q.T)
display("The matrix V appearing in the Right Polar Decomposition of the Deformation Gradient F:")
display("Deformation gradient F =",V)
Fdot = simplify(diff(F,t))
display("Fdot =",Fdot)
L = simplify(Fdot*F.inv())
display("L =",L)
display("L @t=0.5 = ",L.subs({t:0.5}))
display("L @t=1 = ",L.subs({t:1}))
Dd = simplify(1/2*(L+L.T))
display("Symmetric part of L", Dd)
Elagrange = simplify(1/2*(F.T*F-eye(3)))
display("Green Strain =",Elagrange)
Elagrangedot = diff(Elagrange,t)
display("Green Strain rate =",Elagrangedot)
sigmalocal = Matrix([[t*f0/(b*c*(1-t*eb)*(1-t*ec)),0,0],[0,0,0],[0,0,0]])
Cauchy = simplify(Q*sigmalocal*Q.T)
display("Cauchy stress =",Cauchy)
display("Cauchy stress @t=0:",Cauchy.subs({t:0}))
display("Cauchy stress @t=0.5:",Cauchy.subs({t:0.5}))
display("Cauchy stress @t=1:",Cauchy.subs({t:1}))
P = simplify(det(F)*Cauchy*F.T.inv())
display("P =",P)
display("P @ t=0",P.subs({t:0}))
display("P @ t=0.5",P.subs({t:0.5}))
display("P @ t=1",P.subs({t:1}))
S = simplify(F.inv()*P)
display("S =",S)
display("S @ t=0",S.subs({t:0}))
display("S @ t=0.5",S.subs({t:0.5}))
display("S @ t=1",S.subs({t:1}))
e1 = sum([Cauchy[i]*Dd[i] for i in range(9)])
display("P",P,"Fdot",Fdot)
display("D and Cauchy are energy conjugates: dU/dt", simplify(e1))
e2 = sum([P[i]*Fdot[i] for i in range(9)])
display("P",P,"Fdot",Fdot)
display("P and Fdot are energy conjugates: dW/dt", simplify(e2))
e2 = sum([S[i]*Elagrangedot[i] for i in range(9)])
display("S",S,"E_Green",Elagrangedot)
display("S and E_Green are energy conjugates: dW/dt", simplify(e2))

Illustrative Example 3: Extension Followed by Rotation

In this example, the extension of the block with dimensions a, b, and c is applied first where the force is increased linearly from zero to f_0 which is accompanied by a linearly proportional extension \Delta a and two linearly proportional contractions in the opposite directions \Delta b and \Delta c. Afterwards, a rotation of 90 degrees is applied while the force is kept constant but rotating with the block. The force is assumed to be applied in 1 units of time and the rotation is assumed to be applied in 1 units of time. Since the behaviour is time independent, the magnitude of time is redundant. The different stress and strain measures are studied in each step (extension vs. rotation) separately as follows:

Extension
The Deformation Gradient

During the extension phase, the relationship between the deformed coordinates x and the reference coordinates X are described as follows:

    \[\begin{split} x&=\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)=\left(\begin{array}{c}(1+t\varepsilon_a)X_1\\(1-t\varepsilon_b)X_2\\(1-t\varepsilon_c)X_3\end{array}\right)\\ &=\left(\begin{matrix}(1+t\varepsilon_a)&0&0\\0&(1-t\varepsilon_b)&0\\0&0&(1-t\varepsilon_c)\end{matrix}\right)\left(\begin{array}{c}X_1\\X_2\\X_3\end{array}\right) \end{split} \]

Therefore, the deformation gradient and its rate are given by:

    \[\begin{split} F&=\left(\begin{matrix}(1+t\varepsilon_a)&0&0\\0&(1-t\varepsilon_b)&0\\0&0&(1-t\varepsilon_c)\end{matrix}\right)\\ \dot{F}&=\left(\begin{matrix}\varepsilon_a&0&0\\0&\varepsilon_b&0\\0&0&\varepsilon_c\end{matrix}\right) \end{split} \]

The Velocity Gradient

The velocity gradient L is symmetric and is given by:

    \[ L=\dot{F}F^{-1}=\left(\begin{matrix}\frac{\varepsilon_a}{1+t\varepsilon_a}&0&0\\0&\frac{-\varepsilon_b}{1+t\varepsilon_b}&0\\0&0&\frac{-\varepsilon_c}{1-t\varepsilon_c}\end{matrix}\right) \]

In this case, the stretch tensor D is equal to L.

THE GREEN-LAGRANGE STRAIN

The Green strain and its rate are similar to those obtained in both previous examples:

    \[\begin{split} \varepsilon_{\mbox{Green}}&=\frac{1}{2}\left(F^TF-I\right)=\frac{1}{2}\left(U^2-I\right)=\left(\begin{matrix}t\varepsilon_a+\frac{t^2\varepsilon_a^2}{2}&0&0\\0&-t\varepsilon_b+\frac{t^2\varepsilon_b^2}{2}&0\\0&0&-t\varepsilon_c+\frac{t^2\varepsilon_c^2}{2}\end{matrix}\right)\\ \dot{\varepsilon}_{\mbox{Green}}&=\left(\begin{matrix}\varepsilon_a(1+t\varepsilon_a)&0&0\\0&-\varepsilon_b(1-t\varepsilon_b)&0\\0&0&-\varepsilon_c(1-t\varepsilon_c)\end{matrix}\right) \end{split} \]

THE CAUCHY STRESS TENSOR

The Cauchy stress describes the spacial state of stress of the block. In the spacial coordinate system, the Cauchy stress matrix has only one non-zero component and thus at time 0\leq t \leq 1 has the form:

    \[ \sigma=\left(\begin{matrix}\frac{tf_0}{bc(1-t\varepsilon_b)(1-t\varepsilon_c)}&0&0\\0&0&0\\0&0&0\end{matrix}\right) \]

It is important first to note that unlike the load and the deformation are linear in time and thus proportional, the component \sigma_{11} is nonlinear. In fact, it has an increasing slope (i.e., it is convex). This can easily be shown by noting that the second derivative of \sigma_{22} with respect to t is always positive when 0\leq t\leq 1:

    \[ \frac{\mathrm{d}\sigma_{11}}{\mathrm{d}t}=\frac{f_0}{bc(1-t\varepsilon_b)^2(1-t\varepsilon_c)^2}\left(1-\varepsilon_b\varepsilon_c t^2\right) \]

PIOLA KIRCHHOFF STRESS TENSORS

The first Piola Kirchhoff stress tensor P is given by:

    \[ P=\det{(F)}\sigma^TF^{-T}=\left(\begin{matrix}\frac{-tf_0}{bc}&0&0\\0&0&0\\0&0&0\end{matrix}\right) \]

P is not symmetric. The first column gives the spatial components of the spatial force per unit undeformed area acting on the area perpendicular to the reference axis X_1.


The second Piola Kirchhoff stress tensor S is given by:

    \[ S=F^{-1}P=\left(\begin{matrix}\frac{tf_0}{bc(1+t\varepsilon_a)}&0&0\\0&0&0\\0&0&0\end{matrix}\right) \]

As mentioned before, the first column gives the components in the reference configuration of the force vector acting on the area perpendicular to the reference axis X_1 when the force vector is pulled back to the reference configuration. Note that S in this example is similar to S in both previous examples.

Energy Conjugates

The deformation energy in the extension part is similar to that obtained in the previous two examples:

    \[ \mbox{Total Energy}=\int_{a}^{a+\Delta a} \! f \, \mathrm{d}u=\int_{0}^1 \! f\dot{u} \, \mathrm{d}t=\int_{0}^1 \! tf_0\Delta a \, \mathrm{d}t=\frac{f_0\Delta a}{2} \]

The energy per unit volume of the undeformed configuration is given by:

    \[ W=\frac{f_0\Delta a}{2abc} \]

The second Piola Kirchhoff stress tensor and the Green strain tensor are energy conjugates of each other. Note that both measures are identical to the ones obtained in the previous examples! Indeed, W can be obtained by integrating the inner product of S and \dot{\varepsilon}_{\mbox{Green}}:

    \[ W=\int_0^1 \! S_{11}(\dot{\varepsilon}_{\mbox{Green}})_{11} \, \mathrm{d}t=\int_0^1 \! \frac{tf_0\varepsilon_a}{bc} \, \mathrm{d}t=\int_0^1 \! \frac{tf_0\Delta_a}{abc} \, \mathrm{d}t=\frac{f_0\Delta a}{2abc} \]

Alternatively, the same result would be obtained if P and F are used instead as energy conjugates:

    \[ W=\int_0^1 \! P_{11}\dot{F}_{11} \, \mathrm{d}t=\frac{f_0\Delta a}{2abc} \]

The strain energy rate per unit volume of the deformed configuration can be obtained as the inner product of D and \sigma:

    \[ \dot{\overline{U}}= \sigma_{11}D_{11}=\frac{tf_0\Delta a}{abc(1+t\varepsilon_a)(1-t\varepsilon_b)(1-t\varepsilon_c)} \]

which is the same result as the previous two examples! This should not come as a surprise since the applied load and extension for the examples are identical.

ROTATION
THE DEFORMATION GRADIENT

During the rotation phase, the relationship between the deformed coordinates x and the reference coordinates X are described as follows:

    \[ x=\left(\begin{matrix}\cos{\frac{(t-1)\pi}{2}}&\sin{\frac{(t-1)\pi}{2}}&0\\-\sin{\frac{(t-1)\pi}{2}}&\cos{\frac{(t-1)\pi}{2}}&0\\0&0&1\end{matrix}\right)\left(\begin{matrix}(1+\varepsilon_a)&0&0\\0&(1-\varepsilon_b)&0\\0&0&(1-\varepsilon_c)\end{matrix}\right)\left(\begin{array}{c}X_1\\X_2\\X_3\end{array}\right) \]

Where the polar decomposition F=QU is arises naturally. Note that Q is a function of t which takes values 1\leq t \leq 2 while U is constant during that phase.

Therefore, the deformation gradient and its rate are given by:

    \[\begin{split} F&=QU\\ \dot{F}&=\dot{Q}U \end{split} \]

THE VELOCITY GRADIENT
The velocity gradient L is kewsymmetric and is given by:

    \[ L=\dot{F}F^{-1}=\dot{Q}Q^T=\left(\begin{matrix}0&\frac{\pi}{2}&0\\\frac{-\pi}{2}&0&0\\0&0&0\end{matrix}\right) \]

In this case, the stretch tensor D is equal to zero.

THE GREEN-LAGRANGE STRAIN
The Green strain stays constant with its rate equal to zero!

    \[\begin{split} \varepsilon_{\mbox{Green}}&=\frac{1}{2}\left(F^TF-I\right)=\frac{1}{2}\left(U^2-I\right)=\left(\begin{matrix}\varepsilon_a+\frac{\varepsilon_a^2}{2}&0&0\\0&-\varepsilon_b+\frac{\varepsilon_b^2}{2}&0\\0&0&-\varepsilon_c+\frac{\varepsilon_c^2}{2}\end{matrix}\right)\\ \dot{\varepsilon}_{\mbox{Green}}&=\left(\begin{matrix}0&0&0\\0&0&0\\0&0&0\end{matrix}\right) \end{split} \]

THE CAUCHY STRESS TENSOR

The Cauchy stress describes the spacial state of stress of the block. In the spacial coordinate system, the Cauchy stress matrix has the form:

    \[ \sigma=\left(\begin{matrix}s\sin^2{\frac{\pi t}{2}}&\frac{s\sin{\pi t}}{2}&0\\\frac{s\sin{\pi t}}{2}&s\cos^2{\frac{\pi t}{2}}&0\\0&0&0\end{matrix}\right) \]

Where s=\frac{f_0}{bc(1-\varepsilon_b)(1-\varepsilon_c)} which, unlike the previous example, is constant in time.

PIOLA KIRCHHOFF STRESS TENSORS
The first Piola Kirchhoff stress tensor P is given by:

    \[ P=\det{(F)}\sigma^TF^{-T}=\left(\begin{matrix}\frac{f_0\sin{\frac{\pi t}{2}}}{bc}&0&0\\\frac{f_0\cos{\frac{\pi t}{2}}}{bc}&0&0\\0&0&0\end{matrix}\right) \]

The second Piola Kirchhoff stress tensor S is constant (i.e., not a function of t):

    \[ S=F^{-1}P=\left(\begin{matrix}\frac{f_0}{bc(1+\varepsilon_a)}&0&0\\0&0&0\\0&0&0\end{matrix}\right) \]

As mentioned before, the first column gives the components in the reference configuration of the force vector acting on the area perpendicular to the reference axis X_1 when the force vector is pulled back to the reference configuration.

ENERGY CONJUGATES

The deformation energy in the rotation part is equal to zero, i.e, the rotation is not accompanied by any increase (or decrease in the internal energy). Noting that D=\dot{\varepsilon}_{\mbox{Green}}=0, the energy calculated using the Cauchy stress matrix or S during rotation are both equal to zero. Similarly, the same result would be obtained if P and F are used instead as energy conjugates:

    \[ \dot{W}=P_{11}\dot{F}_{11}+P_{12}\dot{F}_{12} =0 \]

View Mathematica Code

(*Extension*)
Print["Extension"]
xe = {xe1, xe2, xe3};
X = {X1, X2, X3};
xe1 = (1 + t*ea) X1;
xe2 = (1 - t*eb) X2;
xe3 = (1 - t*ec) X3;
F = Table[D[xe[[i]], X[[j]]], {i, 1, 3}, {j, 1, 3}];
Print["F"]
F // MatrixForm
Print["Lagrange Strain"]
Elagrange = FullSimplify[1/2 (Transpose[F].F - IdentityMatrix[3])];
Elagrange // MatrixForm
Print["Lagrange Strain Rate"]
Elagrangedot = FullSimplify[D[Elagrange, t]];
Elagrangedot // MatrixForm
Fdot = FullSimplify[D[F, t]];
Print["F dot"]
Fdot // MatrixForm
L = FullSimplify[Fdot.Inverse[F]];
Print["Velocity gradient (L)"]
L // MatrixForm
Dd = FullSimplify[1/2 (L + Transpose[L])];
Print["Symmetric part of Velocity gradient"]
Dd // MatrixForm
Print["Cauchy"]
Cauchy = {{t*f0/(b*c*(1 - t*eb) (1 - t*ec)), 0, 0}, {0, 0, 0}, {0, 0, 0}};
Cauchy // MatrixForm
Print["First Piola"]
P = FullSimplify[Det[F]*Cauchy.Inverse[Transpose[F]]];
P // MatrixForm
Print["Second Piola"]
S = FullSimplify[Inverse[F].P];
S // MatrixForm
Print["Cauchy"]
Cauchy // MatrixForm
Print["D"]
Dd // MatrixForm
Print["D and Cauchy are energy conjugates: dU/dt"]
e1 = FullSimplify[Sum[Cauchy[[i, j]]*Dd[[i, j]], {i, 1, 3}, {j, 1, 3}]] Print["P"]
P // MatrixForm
Print["F Dot"]
Fdot // MatrixForm
Print["P and FDot are energy conjugates: dW/dt"]
e2 = FullSimplify[Sum[P[[i, j]]*Fdot[[i, j]], {i, 1, 3}, {j, 1, 3}]]
Print["S"]
S // MatrixForm
Print["Green Lagrange Strain Rate"]
Elagrangedot // MatrixForm
Print["S and the Lagrange strain rate are energy conjugates: dW/dt"]
e2 = FullSimplify[ Sum[S[[i, j]]*Elagrangedot[[i, j]], {i, 1, 3}, {j, 1, 3}]]
(*Rotation*)
Print["Rotation"]
xe = xe /. t -> 1;
Q = {{Cos[Pi/2*(t-1)], Sin[Pi/2*(t-1)], 0}, {-Sin[Pi/2*(t-1)], Cos[Pi/2*(t-1)],0}, {0, 0, 1}};
x = Q.xe;
F = Table[D[x[[i]], X[[j]]], {i, 1, 3}, {j, 1, 3}];
Print["F"]
F // MatrixForm
Print["Lagrange Strain"]
Elagrange = FullSimplify[1/2 (Transpose[F].F - IdentityMatrix[3])];
Elagrange // MatrixForm
Print["Lagrange Strain Rate"]
Elagrangedot = FullSimplify[D[Elagrange, t]];
Elagrangedot // MatrixForm
Fdot = FullSimplify[D[F, t]];
Print["F dot"]
Fdot // MatrixForm
L = FullSimplify[Fdot.Inverse[F]];
Print["Velocity gradient (L)"]
L // MatrixForm
Dd = FullSimplify[1/2 (L + Transpose[L])];
Print["Symmetric part of Velocity gradient"]
Dd // MatrixForm
Print["Cauchy"]
sigmalocal = Cauchy /. t -> 1;
Cauchy = FullSimplify[Q.sigmalocal.Transpose[Q]];
Cauchy // MatrixForm
Print["First Piola"]
P = FullSimplify[Det[F]*Cauchy.Inverse[Transpose[F]]];
P // MatrixForm
Print["Second Piola"]
S = FullSimplify[Inverse[F].P];
S // MatrixForm
Print["Cauchy"]
Cauchy // MatrixForm
Print["D"]
Dd // MatrixForm
Print["D and Cauchy are energy conjugates: dU/dt"]
e1 = FullSimplify[Sum[Cauchy[[i, j]]*Dd[[i, j]], {i, 1, 3}, {j, 1, 3}]]
Print["P"]
P // MatrixForm
Print["F Dot"]
Fdot // MatrixForm
Print["P and FDot are energy conjugates: dW/dt"]
e2 = FullSimplify[Sum[P[[i, j]]*Fdot[[i, j]], {i, 1, 3}, {j, 1, 3}]]
Print["S"]
S // MatrixForm
Print["Green Lagrange Strain Rate"]
Elagrangedot // MatrixForm
Print["S and the Lagrange strain rate are energy conjugates: dW/dt"]
e2 = FullSimplify[ Sum[S[[i, j]]*Elagrangedot[[i, j]], {i, 1, 3}, {j, 1, 3}]]

View Python Code

import sympy as sp
import numpy as np
from sympy import Matrix, simplify, diff, eye, det
display("Extension")
theta = sp.symbols("theta")
X1,X2,X3 = sp.symbols("X_1 X_2 X_3")
X = Matrix([X1,X2,X3])
a,b,c = sp.symbols("a b c")
ea,eb,ec,t = sp.symbols("epsilon_a epsilon_b epsilon_c t")
f0 = sp.symbols("f_0")
xe1 = (1+t*ea)*X1
xe2 = (1-t*eb)*X2
xe3 = (1-t*ec)*X3
xe = Matrix([xe1, xe2, xe3])
F = Matrix([[diff(i,j) for j in X] for i in xe])
display("F =",F)
Elagrange = simplify(1/2*(F.T*F-eye(3)))
display("Lagrange Strain =",Elagrange)
Elagrangedot = diff(Elagrange,t)
display("Lagrange Strain rate =",Elagrangedot)
Fdot = simplify(diff(F,t))
display("Fdot =",Fdot)
L = simplify(Fdot*F.inv())
display("Velocity gradient (L) =",L)
Dd = simplify(1/2*(L+L.T))
display("Symmetric part of L", Dd)
Cauchy = Matrix([[t*f0/(b*c*(1-t*eb)*(1-t*ec)),0,0],[0,0,0],[0,0,0]])
display("Cauchy =",Cauchy)
P = simplify(det(F)*Cauchy*F.T.inv())
display("First Piola =",P)
S = simplify(F.inv()*P)
display("Second Piola =",S)
e1 = sum([Cauchy[i]*Dd[i] for i in range(9)])
display("Cauchy",Cauchy,"Dd",Dd)
display("D and Cauchy are energy conjugates: dU/dt", simplify(e1))
e2 = sum([P[i]*Fdot[i] for i in range(9)])
display("P",P,"Fdot",Fdot)
display("P and Fdot are energy conjugates: dW/dt", simplify(e2))
e2 = sum([S[i]*Elagrangedot[i] for i in range(9)])
display("S",S,"E_Green",Elagrangedot)
display("S and E_Green are energy conjugates: dW/dt", simplify(e2))
display("Rotation")
xe = xe.subs({t:1})
Q = Matrix([[sp.cos(theta*(t-1)), sp.sin(theta*(t-1)),0],
            [-sp.sin(theta*(t-1)),sp.cos(theta*(t-1)), 0],
            [0,0,1]])
Q = Q.subs({theta:sp.pi/2})
display("Q =", Q)
x = Q*xe
F = Matrix([[diff(i,j) for j in X] for i in x])
display("F =",F)
Elagrange = simplify(1/2*(F.T*F-eye(3)))
display("Lagrange Strain =",Elagrange)
Elagrangedot = diff(Elagrange,t)
display("Lagrange Strain rate =",Elagrangedot)
Fdot = simplify(diff(F,t))
display("Fdot =",Fdot)
L = simplify(Fdot*F.inv())
display("Velocity gradient (L) =",L)
Dd = simplify(1/2*(L+L.T))
display("Symmetric part of L", Dd)
sigmalocal = Cauchy.subs({t:1})
Cauchy = simplify(Q*sigmalocal*Q.T)
display("Cauchy =",Cauchy)
P = simplify(det(F)*Cauchy*F.T.inv())
display("First Piola =",P)
S = simplify(F.inv()*P)
display("Second Piola =",S)
e1 = sum([Cauchy[i]*Dd[i] for i in range(9)])
display("Cauchy",Cauchy,"Dd",Dd)
display("D and Cauchy are energy conjugates: dU/dt", simplify(e1))
e2 = sum([P[i]*Fdot[i] for i in range(9)])
display("P",P,"Fdot",Fdot)
display("P and Fdot are energy conjugates: dW/dt", simplify(e2))
e2 = sum([S[i]*Elagrangedot[i] for i in range(9)])
display("S",S,"E_Green",Elagrangedot)
display("S and E_Green are energy conjugates: dW/dt", simplify(e2))

Video:

Quiz-Strain Energy

Problems

Let a deformation be described by F=Q(t)U, i.e., a rotation that is a function of time and an extension that is constant. If P is the first Piola Kirchhoff stress tensor, show that \dot{W}=\mbox{Trace}(P\dot{F}^T)=0.

Leave a Reply

Your email address will not be published.