Mathematical Preliminaries: Mathematical Symbols
Learning Outcomes
- Identify the basic symbols of mathematics that will be used in the lecture
- Define sets
- Define functions
Mathematical Symbols
The following are the mathematical symbols used throughout these online material.
- Curly brackets are used to designate sets. For example
 is the set of the three elements 1, 2, and 3.
is the set of the three elements 1, 2, and 3. - We use the symbol
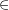 to designate elements in sets. For example, if
to designate elements in sets. For example, if  , then
, then 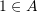 .
. - The symbol
 means “subset of” and is used to indicate that the elements of one set are elements of another set. For example, if
means “subset of” and is used to indicate that the elements of one set are elements of another set. For example, if  and
and 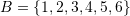 , then
, then 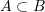 .
. - Sets can be defined using properties listed within the curly brackets. For example, we can define the set
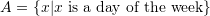 . This means that
. This means that 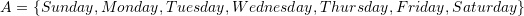 .
. 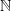 is used to designate the set of natural numbers starting from 1. i.e.,
is used to designate the set of natural numbers starting from 1. i.e., 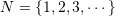 .
.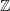 is used to designate the set of integers. i.e.,
is used to designate the set of integers. i.e., 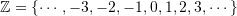 .
.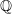 is used to designate the set of rational numbers. i.e.,
is used to designate the set of rational numbers. i.e., 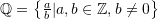 .
.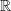 is used to designate the set of real numbers.
is used to designate the set of real numbers.- Box brackets are used to designate (closed) intervals in real numbers. For example,
![Rendered by QuickLaTeX.com A=[0,1]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-838b321ec17052577240af06f4f1bb76_l3.png) is the set of real numbers between 0 and 1 and including both 0 and 1.
is the set of real numbers between 0 and 1 and including both 0 and 1. - Round brackets are used to designate (open) intervals in real numbers. for example,
![Rendered by QuickLaTeX.com B=(0,1]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-1b1e12408ab515c5d0004819c9fcb9f0_l3.png) is the set of real numbers between 0 and 1 and including 1.
is the set of real numbers between 0 and 1 and including 1. - The symbol
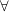 means “for every” and is usually used to designate a property of all the elements of a set. For example, if we say that
means “for every” and is usually used to designate a property of all the elements of a set. For example, if we say that  , we can describe the fact that all the elements in
, we can describe the fact that all the elements in 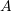 are greater than zero by stating:
are greater than zero by stating: 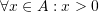 .
. - The symbol
 means “exists” and is used to identify particular elements in sets. For example, if
means “exists” and is used to identify particular elements in sets. For example, if  we can say that
we can say that 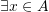 such that
such that 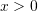 , i.e., there exists an element in the set
, i.e., there exists an element in the set 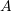 which is greater than 0.
which is greater than 0. - The symbol
 means “exists and unique” and is used to identify a unique element in a set. For example, if
means “exists and unique” and is used to identify a unique element in a set. For example, if  we can say that
we can say that 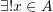 such that
such that 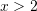 , i.e., there exists one element and one element only in the set
, i.e., there exists one element and one element only in the set 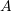 which is greater than 2.
which is greater than 2. - To define functions or maps between sets, we use
 . If
. If 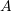 is a set and
is a set and 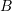 is another set, then a function that maps elements of
is another set, then a function that maps elements of 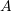 into elements of
into elements of 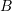 is defined with the notation
is defined with the notation 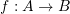 .
. - If
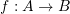 , then, the arrow
, then, the arrow  is used to designate that a function
is used to designate that a function 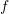 maps the element
maps the element 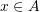 to
to 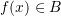 as follows
as follows  .
. - The symbol
 is used in many contexts. One of them is the cross product which will be defined later. Another is for defining the set of ordered pairs. For example, if
is used in many contexts. One of them is the cross product which will be defined later. Another is for defining the set of ordered pairs. For example, if 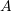 and
and 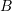 are two sets. Then, the set
are two sets. Then, the set 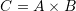 is the set made of ordered pairs
is the set made of ordered pairs 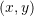 with
with 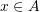 and
and  . For example if
. For example if 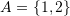 and
and 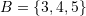 , then
, then 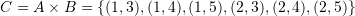 . The set
. The set 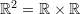 is the set of ordered pairs of real numbers and geometrically designates a plane. Similarly,
is the set of ordered pairs of real numbers and geometrically designates a plane. Similarly, 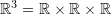 is the set representing the three dimensional space.
is the set representing the three dimensional space. 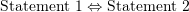 is used to designate equivalence of statements 1 and 2(if and only if). For example:
is used to designate equivalence of statements 1 and 2(if and only if). For example: 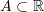 is equivalent to
is equivalent to 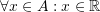 . So, this can be written as:
. So, this can be written as: 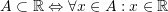 .
.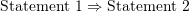 is used to describe that statements 1 leads to statement 2. For example:
is used to describe that statements 1 leads to statement 2. For example:  leads to the statement
leads to the statement  . So, this can be written as:
. So, this can be written as: 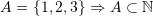 .
.- The Kronecker delta
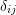 is a special symbol which gives a value of either 0 or 1 depending on the subscripts
is a special symbol which gives a value of either 0 or 1 depending on the subscripts  and
and 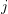 . Usually
. Usually  and
and 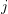 can take values of 1, 2, or 3 and
can take values of 1, 2, or 3 and
![Rendered by QuickLaTeX.com \[ \delta_{ij}= \begin{cases} 1 & i=j\\ 0 & i\neq j \end{cases} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7a359205b3390e5276f42ab3fdfc0887_l3.png)
- The alternator
 is a special symbol which gives a value of either 0, 1, or -1 depending on the subscripts
is a special symbol which gives a value of either 0, 1, or -1 depending on the subscripts  ,
, 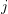 , and
, and  . Usually
. Usually  ,
, 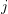 , and
, and  can take values of 1, 2, or 3 and
can take values of 1, 2, or 3 and
![Rendered by QuickLaTeX.com \[ \varepsilon_{ijk}= \begin{cases} 1 & i,j,k \mbox{ is a cyclic permutation of 1, 2, 3}\\ -1 & i,j,k \mbox{ is a noncyclic permutation of 1, 2, 3}\\ 0 & \mbox{Otherwise} \end{cases} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f28ef771f996180bf4032b4cdefa7b2c_l3.png)
- Unless stated explicitly, we do not differentiate between the column or row representation of vectors in
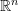 . The curly brackets are also used for the row representation of vectors to be consistent with how Mathematica defines a vector. Therefore, the following are equivalent for the three dimensional vector
. The curly brackets are also used for the row representation of vectors to be consistent with how Mathematica defines a vector. Therefore, the following are equivalent for the three dimensional vector  with components
with components 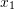 ,
,  , and
, and 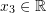 :
:![Rendered by QuickLaTeX.com \[ x=\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)=\{x_1,x_2,x_3\}=(x_1,x_2,x_3) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-89d6adac461112e2847a6eea383217eb_l3.png)
- The reader should differentiate between vectors and sets depending on the context.

very useful for the start
Great summary
Great effort