Open Educational Resources

Hyperelastic Materials: Examples of Isotropic Hyperelastic Potential Energy Functions

Hyperelastic potential energy functions are often developed by proposing certain forms and then calibrating material coefficients, according to experimental results. The proposed forms naturally have to abide by the principle of material frame-indifference and other physical restrictions, such as isotropy. There are many examples of hyperelastic potential energy functions. An interested reader should consult a more detailed reference [for example, Holzapfel, G. (2000) and Ogden, R. (1997)]. In this section, three forms of hyperelastic potential energy functions of isoptric incompressible and compressible materials will be introduced along with the expression of the associated stress matrices.

1) Incompressible and Compressible Hyperelastic Isotropic Strain Energy Potential Functions in Terms of the Invariants of 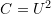C=U^2

If W is a function of I_1(U^2)=\lambda_1^2+\lambda_2^2+\lambda_3^2, I_2(U^2)=\lambda_1^2\lambda_2^2+\lambda_2^2\lambda_3^2+\lambda_1^2\lambda_3^2, and J=\det(F)=\lambda_1\lambda_2\lambda_3, then the expression for the Piola Kirchhoff stress tensor P and the Cauchy stress tensor \sigma can be given as follows:

    \[ W=W(I_1, I_2, J) \]

The general form of first Piola Kirchhoff stress tensor is given by:

    \[ P=\frac{\partial W}{\partial F}=\frac{\partial W}{\partial I_1}\frac{\partial I_1}{\partial F}+\frac{\partial W}{\partial I_2}\frac{\partial I_2}{\partial F}+\frac{\partial W}{\partial J}\frac{\partial J}{\partial F} \]

The general form of Cauchy stress tensor is given by:

    \[ \sigma=\sigma^T=\frac{1}{J}PF^T=\frac{1}{J}\frac{\partial W}{\partial F}F^T=\frac{1}{J}\left(\frac{\partial W}{\partial I_1}\frac{\partial I_1}{\partial F}+\frac{\partial W}{\partial I_2}\frac{\partial I_2}{\partial F}+\frac{\partial W}{\partial J}\frac{\partial J}{\partial F}\right)F^T \]

In order to find the exact expressions for the stress tensors, the following equalities will be used. Their proof can be found in statement 1 of the matrix calculus page.

    \[ \begin{split} &\frac{\partial I_1}{\partial F}=2F\\ &\frac{\partial I_2}{\partial F}=2I_1F-2FF^TF\\ &\frac{\partial J}{\partial F}=JF^{-T} \end{split} \]

By substitution into the equations of P and \sigma, the following is obtaiend:

    \[ P=\frac{\partial W}{\partial I_1}2F+\frac{\partial W}{\partial I_2}(2I_1F-2FF^TF)+\frac{\partial W}{\partial J}JF^{-T} \]

(2)   \begin{equation*} \sigma=\frac{2}{J}\left(\frac{\partial W}{\partial I_1}+I_1\frac{\partial W}{\partial I_2}\right)FF^T-\frac{2}{J}\frac{\partial W}{\partial I_2}(FF^TFF^T)+\frac{\partial W}{\partial J}I \end{equation*}

Incompressible Neo-Hookean Material Model

This material model has the following expression for the strain energy function:

    \[W=2\mu(I_1 (U^2 )-3)\]

with J=1 and \mu is a material constant. For this form we have \frac{\partial W}{\partial I_1}=2\mu, \frac{\partial W}{\partial I_2}=0, and \frac{\partial W}{\partial J}=0. As the material is incompressible, the stress matrices are function of an unknown hydrostatic stress p. Therefore, the first Piola Kirchhoff stress and the Cauchy stress tensors are given by:

    \[ \begin{split}&P=4\mu F+JpF^{-T}\\ &\sigma=4\mu FF^T+pI \end{split} \]

Note that the unknown hydrostatic stress p can only be obtained from the boundary conditions of the stress. The hydrostatic stress can be incorporated in the energy form by adding the term p(J-1) to the energy function:

    \[W=2\mu(I_1 (U^2 )-3)+p(J-1)\]

In this case, the hydrostatic stress term in the expressions for the stresses is obtained directly. Notice as well that the boundary conditions of zero stresses lead to a non-zero value for p for this material model. In the case of a F=Q where Q is a rotation with no applied stresses, then, p=-4\mu will ensure that \sigma=0.

Incompressible Mooney-Rivlin Material Model

This material model has the following expression for the strain energy function

    \[W=\frac{\mu_1}{2}(I_1 (U^2 )-3)+\frac{\mu_2}{2}(I_2 (U^2 )-3)\]

with J=1 and \mu_1, \mu_2 are material constants. For this form we have \frac{\partial W}{\partial I_1}=\frac{\mu_1}{2}, \frac{\partial W}{\partial I_2}=\frac{\mu_2}{2}, and \frac{\partial W}{\partial J}=0. As the material is incompressible, the stress matrices are function of an unknown hydrostatic stress p. Therefore, the first Piola Kirchhoff stress and the Cauchy stress tensors are given by:

    \[ \begin{split}&P=\mu_1 F+\mu_2(I_1F-FF^TF)+JpF^{-T}\\ &\sigma=\mu_1 FF^T+\mu_2(I_1FF^T-FF^TFF^T)+pI \end{split} \]

Similarly, the unknown hydrostatic stress p can only be obtained from the boundary conditions of the stress. The hydrostatic stress can be incorporated in the energy form by adding the term p(J-1) to the energy function:

    \[W=\frac{\mu_1}{2}(I_1 (U^2 )-3)+\frac{\mu_2}{2}(I_2 (U^2 )-3)+p(J-1)\]

In this case, the hydrostatic stress term in the expressions for the stresses is obtained directly. Notice as well that the boundary conditions of zero stresses lead to a non-zero value for p for this material model. In the case of a F=Q where Q is a rotation with no applied stresses, then, p=-\mu_1 - 2\mu_2 will ensure that \sigma=0.

Compressible Neo-Hookean Material Model

Several forms of the compressible Neo-Hookean material models exist in the literature. One of the examples of such models has the form:

    \[ W=2\mu_1(I_1 (U^2 )-3-2\ln{J})+\mu_2(J-1)^2 \]

with \mu_1,\mu_2 are material constants. Notice that the term (J-1)^2 ensures that when J increases above the value of 1, the strain energy increases without an upper bound. Similarly, the term -2\ln{J} ensures that when the J approaches zero, the strain energy approaches infinity. The current form of W ensures that it attains the minimum value of 0 for any rigid rotation. Some similar forms of the strain energy contain the term \left(J-1-2\ln{J}\right) which attains a minimum of zero when J=1 and approaches infinity when J approaches infinity or zero.

For this form we have \frac{\partial W}{\partial I_1}=2\mu_1, \frac{\partial W}{\partial I_2}=0, and \frac{\partial W}{\partial J}=-4\frac{\mu_1}{J}+2\mu_2(J-1). Therefore, the first Piola Kirchhoff stress and the Cauchy stress tensors are given by:

    \[ \begin{split}&P=4\mu_1(F-F^{-T})+2\mu_2J(J-1)F^{-T}\\ &\sigma=4\frac{\mu_1}{J}\left(FF^T-I\right)+2\mu_2(J-1)I \end{split} \]

In the case of a F=Q where Q is a rotation with no applied stresses, then, \sigma=P=0.

2) Incompressible And Compressible Hyperelastic Isotropic Strain Energy Potential Functions in Terms of the Principal Stretches 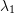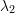\lambda_1, \lambda_2, and \lambda_3

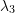
If W is a function of \lambda_1, \lambda_2, and \lambda_3, then the expression for the Piola Kirchhoff stress tensor P and the Cauchy stress tensor \sigma can be given as follows:

    \[ W=W(\lambda_1,\lambda_2,\lambda_3) \]

The general form of first Piola Kirchhoff stress tensor is given by:

    \[ P=\frac{\partial W}{\partial F}=\frac{\partial W}{\partial \lambda_1}\frac{\partial \lambda_1}{\partial F}+\frac{\partial W}{\partial \lambda_2}\frac{\partial \lambda_2}{\partial F}+\frac{\partial W}{\partial \lambda_3}\frac{\partial \lambda_3}{\partial F} \]

The general form of Cauchy stress tensor is given by:

    \[ \sigma=\sigma^T=\frac{1}{J}PF^T=\frac{1}{J}\frac{\partial W}{\partial F}F^T=\frac{1}{J}\left(\frac{\partial W}{\partial \lambda_1}\frac{\partial \lambda_1}{\partial F}+\frac{\partial W}{\partial \lambda_2}\frac{\partial \lambda_2}{\partial F}+\frac{\partial W}{\partial \lambda_3}\frac{\partial \lambda_3}{\partial F}\right)F^T \]

In order to find the exact expressions for the stress tensors, the singular value decomposition of the deformations gradient will be used:

    \[ F=RQD Q^T \]

Where, R,Q\in\mathbb{M}^3 are rotation matrices and D\in\mathbb{M}^3 is a diagonal matrix with entries:

    \[ D=\left(\begin{array}{ccc} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_3 \end{array} \right) \]

The following component form equalities can then be deduced and their proof can be found in statement 2 of the matrix calculus page.

    \[ \begin{split} &\frac{\partial \lambda_1}{\partial F_{ij}}=\sum_{k=1}^3Q_{k1}R_{ik}Q_{j1}\\ &\frac{\partial \lambda_2}{\partial F_{ij}}=\sum_{k=1}^3Q_{k2}R_{ik}Q_{j2}\\ &\frac{\partial \lambda_3}{\partial F_{ij}}=\sum_{k=1}^3Q_{k3}R_{ik}Q_{j3} \end{split} \]

Alternatively, the following tensor form of the derivatives of \lambda_1, \lambda_2, and \lambda_3 with respect to F can be used and their proof can be found in statement 2 of the matrix calculus page.

    \[ \frac{\partial \lambda_i}{\partial F}=(n_i\otimes N_i) \]

where n_i and N_i are the eigenvectors of V^2=B and U^2=C, respectively, and corresponding to the eigenvalue \lambda_i^2.

By substituting this tensorial form into the equations of P and \sigma, and using the equality J=\lambda_1\lambda_2\lambda_3 the following is obtained:

    \[ P=\frac{\partial W}{\partial \lambda_1}(n_1\otimes N_1)+\frac{\partial W}{\partial \lambda_2}(n_2\otimes N_2)+\frac{\partial W}{\partial \lambda_3}(n_3\otimes N_3) \]

(3)   \begin{equation*} \begin{split} \sigma &=\frac{1}{J}\left(\frac{\partial W}{\partial \lambda_1}(n_1\otimes N_1)+\frac{\partial W}{\partial \lambda_2}(n_2\otimes N_2)+\frac{\partial W}{\partial \lambda_3}(n_3\otimes N_3)\right)(\lambda_1(N_1\otimes n_1)\\ &+\lambda_2(N_2\otimes n_2)+\lambda_3(N_3\otimes n_3))\\ &=\frac{1}{\lambda_2\lambda_3}\frac{\partial W}{\partial \lambda_1}(n_1\otimes n_1)+\frac{1}{\lambda_1\lambda_3}\frac{\partial W}{\partial \lambda_2}(n_2\otimes n_2)+\frac{1}{\lambda_1\lambda_2}\frac{\partial W}{\partial \lambda_3}(n_3\otimes n_3) \end{split} \end{equation*}

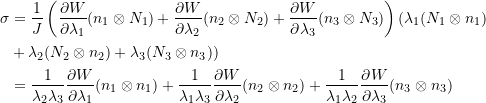
Incompressible Ogden Material Model

:

This material model has the following expression for the strain energy function

    \[ W=\sum_{n=1}^N\frac{\mu_n}{\alpha_n}\left(\lambda_1^{\alpha_n}+\lambda_2^{\alpha_n}+\lambda_3^{\alpha_n}\right) \]

with J=1 and \forall n\leq N \mu_n, \alpha_n are material constants. For this material model, given a general deformation gradient F, the expressions for the stress tensors are more involved and require utilizing the singular value decomposition \Box of the deformation gradient.

Similar to the other incompressible material models, the unknown hydrostatic stress p can only be obtained from the boundary conditions of the stress. The hydrostatic stress can be incorporated in the energy form by adding the term p(J-1) to the energy function:

    \[ W=\sum_{n=1}^N\frac{\mu_n}{\alpha_n}\left(\lambda_1^{\alpha_n}+\lambda_2^{\alpha_n}+\lambda_3^{\alpha_n}\right)+p(J-1) \]

In this case, the hydrostatic stress term in the expressions for the stresses is obtained directly.

Compressible Ogden Material Model

The compressible Ogden material model can be obtained by a simple modification of the previous model:

    \[W=\sum_{n=1}^N\frac{\mu_n}{\alpha_n}\left(\lambda_1^{\alpha_n}+\lambda_2^{\alpha_n}+\lambda_3^{\alpha_n}\right)+g(J)\]

where g(J) can be any function of J that attains a minimum at J=1 and increases unboundedly when J approaches infinity or zero. An example of such function would be g(J)=\mu_J(J-1-2\ln{J}) where \mu_J is a material constant.

3) Compressible Hyperelastic Isotropic Strain Energy Potential Functions With An Additive Decomposition

Some authors to write W as a function of \overline{I_1}\left(\overline{F^T}\overline{F}\right), \overline{I_2}\left(\overline{F^T}\overline{F}\right), and J=\det(F), in the following form:

    \[ W=W_1\left(\overline{I_1}, \overline{I_2}\right)+W_2(J) \]

where W_1 and W_2 are the two components which represent an “isochoric” or “deviatoric” component and a “volumetric” component respectively. The general form of first Piola Kirchhoff stress tensor in this case is given by:

    \[ P=\frac{\partial W}{\partial F}=\frac{\partial W}{\partial \overline{I_1}}\frac{\partial \overline{I_1}}{\partial F}+\frac{\partial W}{\partial \overline{I_2}}\frac{\partial \overline{I_2}}{\partial F}+\frac{\partial W}{\partial J}\frac{\partial J}{\partial F} \]

The general form of Cauchy stress tensor in this case is given by:

    \[ \sigma=\sigma^T=\frac{1}{J}PF^T=\frac{1}{J}\frac{\partial W}{\partial F}F^T=\frac{1}{J}\left(\frac{\partial W}{\partial \overline{I_1}}\frac{\partial \overline{I_1}}{\partial F}+\frac{\partial W}{\partial \overline{I_2}}\frac{\partial \overline{I_2}}{\partial F}+\frac{\partial W}{\partial J}\frac{\partial J}{\partial F}\right)F^T \]

In order to find the exact expressions for the stress tensors, the following equalities will be used. Their proof can be found statement 3 of the matrix calculus page.

    \[ \begin{split} &\frac{\partial \overline{I_1}}{\partial F}=J^{-\frac{2}{3}}\left(2F-\frac{2I_1}{3}F^{-T}\right)\\ &\frac{\partial \overline{I_2}}{\partial F}=J^{-\frac{4}{3}}\left(2I_1F-2FF^TF-\frac{4I_2}{3}F^{-T}\right) \end{split} \]

Where I_1,I_2 are the first and second invariants of F^TF respectively and \overline{F}=J^{-\frac{1}{3}}F.
By substituting into the expressions for P and \sigma, the following is obtained:

    \[ \begin{split} P& =J^{-\frac{2}{3}}\frac{\partial W}{\partial \overline{I_1}}\left(2F-\frac{2I_1}{3}F^{-T}\right)+J^{-\frac{4}{3}}\frac{\partial W}{\partial \overline{I_2}}\left(2I_1F-2FF^TF-\frac{4I_2}{3}F^{-T}\right)+\frac{\partial W}{\partial J}JF^{-T}\\ &= 2J^{-\frac{2}{3}}\left(\frac{\partial W}{\partial \overline{I_1}}+J^{-\frac{2}{3}}I_1\frac{\partial W}{\partial \overline{I_2}}\right)F-2J^{-\frac{4}{3}}\frac{\partial W}{\partial \overline{I_2}}FF^TF\\ & +\left(-J^{-\frac{2}{3}}\frac{2I_1}{3}\frac{\partial W}{\partial \overline{I_1}}-\frac{4I_2}{3}J^{-\frac{4}{3}}\frac{\partial W}{\partial \overline{I_2}} +J\frac{\partial W}{\partial J}\right)F^{-T} \end{split} \]

(4)   \begin{equation*} \begin{split} \sigma=& 2J^{-\frac{5}{3}}\left(\frac{\partial W}{\partial \overline{I_1}}+J^{-\frac{2}{3}}I_1\frac{\partial W}{\partial \overline{I_2}}\right)FF^T-2J^{-\frac{7}{3}}\frac{\partial W}{\partial \overline{I_2}}FF^TFF^T\\ &+\left(-J^{-\frac{5}{3}}\frac{2I_1}{3}\frac{\partial W}{\partial \overline{I_1}}-\frac{4I_2}{3}J^{-\frac{7}{3}}\frac{\partial W}{\partial \overline{I_2}}+\frac{\partial W}{\partial J}\right)I \end{split} \end{equation*}

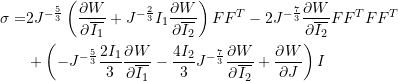
Compressible Neo-Hookean Material Model

This material model has the following expression for the strain energy function:

    \[W=C_{10}\left(\overline{I_1} -3\right)+\frac{1}{D}(J-1)^2\]

where C_{10} and D are material constants. For this form we have \frac{\partial W}{\partial \overline{I_1}}=C_{10}, \frac{\partial W}{\partial I_2}=0, and \frac{\partial W}{\partial J}=\frac{2}{D}(J-1). Therefore, the first Piola Kirchhoff stress and the Cauchy stress tensors are given by:

    \[ \begin{split}&P=C_{10}J^{-\frac{2}{3}}\left(2F-\frac{2I_1}{3}F^{-T}\right)+\frac{2}{D}(J-1)JF^{-T}\\ &\sigma=C_{10}J^{-\frac{5}{3}}\left(2FF^T-\frac{2I_1}{3}I\right)+\frac{2}{D}(J-1)I \end{split} \]

Compressible Mooney-Rivlin Material Model

This material model has the following expression for the strain energy function:

    \[W=C_{10}\left(\overline{I_1} -3\right)+C_{01}\left(\overline{I_2}-3\right)+\frac{1}{D}(J-1)^2\]

where C_{10}, C_{01}, and D are material constants. For this form we have \frac{\partial W}{\partial \overline{I_1}}=C_{10}, \frac{\partial W}{\partial I_2}=C_{01}, and \frac{\partial W}{\partial J}=\frac{2}{D}(J-1). Therefore, the first Piola Kirchhoff stress and the Cauchy stress tensors are given by:

    \[ \begin{split}&P=C_{10}J^{-\frac{2}{3}}\left(2F-\frac{2I_1}{3}F^{-T}\right)+C_{01}J^{-\frac{4}{3}}\left(2I_1F-2FF^TF-\frac{4I_2}{3}F^{-T}\right)+\frac{2}{D}(J-1)JF^{-T}\\ &\sigma=C_{10}J^{-\frac{5}{3}}\left(2FF^T-\frac{2I_1}{3}I\right)+C_{01}J^{-\frac{7}{3}}\left(2I_1FF^T-2FF^TFF^T-\frac{4I_2}{3}I\right)+\frac{2}{D}(J-1)I \end{split} \]

4) Saint-Venant Kirchhoff Mateiral Model

The Saint-Venant Kirchhoff hyperelastic material model is an extension of the linear elastic material model in which large rotations are accounted for by utilizing the Green strain tensor instead of the small strain tensor. The book by Philippe Ciarlet shows how this material model arises naturally when a Taylor expansion is used for the stress tensor or the strain energy function of isotropic hyperelastic materials close to a natural state (i.e., at small strains). The strain energy function of this model is defined as:

    \[ W(\varepsilon_{\text{Green}})=\frac{\lambda}{2}\left(\text{Tr}(\varepsilon_{\text{Green}})\right)^2+\mu \text{Tr}(\varepsilon_{\text{Green}}^2) \]

In this case, the second Piola-Kirchhoff stress is given by (See exercises 2 and 3 below):

    \[ S=\lambda \text{Tr}(\varepsilon_{\text{Green}})I+2\mu \varepsilon_{\text{Green}} \]

Where \lambda and \mu are Lamé’s constants. A reader should compare this form to that of a linear elastic isotropic material as given in this section. This material model is ubiquitously used for beams when large rotations need to be accounted for.

Leave a Reply

Your email address will not be published.