Stress: Cauchy Sensor Tensor
Learning Outcomes
- Identify that in a continuum, stress at a point is defined using a symmetric matrix, and not a number. Describe what the components of the matrix mean.
- Identify that the stress matrix is symmetric. Recognize the implications as having a coordinate system in which no shear stresses appear in the matrix. Employ the process of diagonalization of a symmetric matrix to find this coordinate system.
- Compute the normal and shear stresses on different planes using a stress matrix.
Definitions
The topics presented here were first introduced by Augustin-Louis Cauchy in the nineteenth century. Cauchy introduced the idea of stress or traction vectors which are force vectors per unit area. He then introduced the stress as a ![]() symmetric matrix. The stress matrix is perhaps one of the early concepts that promoted the study of vectors and matrices. The word
symmetric matrix. The stress matrix is perhaps one of the early concepts that promoted the study of vectors and matrices. The word ![]() that is used to describe a matrix is perhaps due to the fact, as will be shown here, that the stress tensor acts on area vectors to produce traction vectors.
that is used to describe a matrix is perhaps due to the fact, as will be shown here, that the stress tensor acts on area vectors to produce traction vectors.
Traction Vector
Before defining the “Stress Tensor/Matrix”, we first define the force vector per unit area. The force vector per unit area is termed the “Traction Vector”. The traction vector at a point inside a body can be defined after removing the adjacent material and considering that a force vector ![]() is exerted by the removed material on an area
is exerted by the removed material on an area ![]() surrounding that point. The traction vector
surrounding that point. The traction vector ![]() at this point considering the surface with the normal vector
at this point considering the surface with the normal vector ![]() is then (Figure 1 ):
is then (Figure 1 ):
![]()
By invoking Newton’s third law of motion (every action has an equal and opposite reaction), the traction vector acting on the corresponding point on the removed material whose normal vector is -n is equal to (Figure 1 ):
![]()
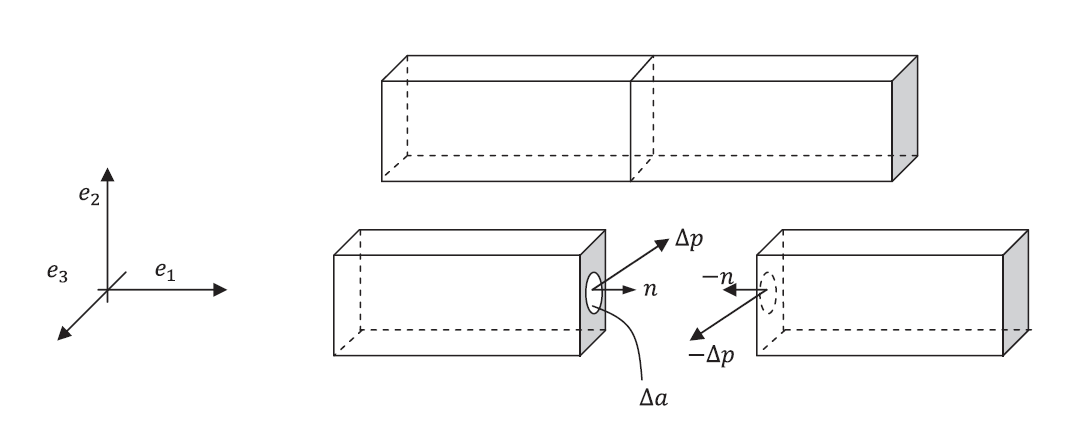
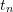 acting at a point in an area with normal vector
acting at a point in an area with normal vector 
The Cauchy Stress Tetrahedron
In this section we present the proof according to the French Mathematician Augustin-Louis Cauchy that shows that the state of stress at a particular point inside a continuum is well defined using a ![]() symmetric matrix, which is called the stress matrix or stress tensor. Knowing this matrix allows the calculation of any traction vector on any plane passing through that point. First, we consider an infinitesimal cube (Figure 2) at a point inside the material and we consider the three faces perpendicular to the three basis vectors
symmetric matrix, which is called the stress matrix or stress tensor. Knowing this matrix allows the calculation of any traction vector on any plane passing through that point. First, we consider an infinitesimal cube (Figure 2) at a point inside the material and we consider the three faces perpendicular to the three basis vectors ![]() ,
, ![]() , and
, and ![]() . The force per unit area vector on each of these three faces has three components and therefore, in total, there are nine components. We then set
. The force per unit area vector on each of these three faces has three components and therefore, in total, there are nine components. We then set ![]() as the stress component on the face with normal i and acting in the direction
as the stress component on the face with normal i and acting in the direction ![]() . Notice that in some textbooks, this definition could be reversed. A tetrahedron can be formed by considering four faces perpendicular to
. Notice that in some textbooks, this definition could be reversed. A tetrahedron can be formed by considering four faces perpendicular to ![]() ,
, ![]() ,
, ![]() , and an arbitrary vector
, and an arbitrary vector ![]() (Figure 3). We are going to use the stress components to find the traction vector acting on the arbitrary area whose normal vector is
(Figure 3). We are going to use the stress components to find the traction vector acting on the arbitrary area whose normal vector is ![]() . If
. If ![]() is the area of the surface with normal
is the area of the surface with normal ![]() , then:
, then:
![]()
where ![]() ,
, ![]() , and
, and ![]() are the areas of the triangular faces perpendicular to
are the areas of the triangular faces perpendicular to ![]() ,
, ![]() , and
, and ![]() respectively (Can you derive the above formula using the properties of the cross product?). Setting
respectively (Can you derive the above formula using the properties of the cross product?). Setting ![]() with
with ![]() :
:
![]()
Invoking Newton’s equations of equilibrium, the sum of the forces acting on the tetrahedron (including the gravity force ![]() where
where ![]() ,
, ![]() , and
, and ![]() are the components of the gravity acceleration) are equal to its mass multiplied by its acceleration vector
are the components of the gravity acceleration) are equal to its mass multiplied by its acceleration vector ![]() . Therefore:
. Therefore:
![]()
![]()
![]()
The mass ![]() can be related to the height
can be related to the height ![]() of the tetrahedron perpendicular to
of the tetrahedron perpendicular to ![]() using the mass density
using the mass density ![]() as follows:
as follows:
![]()
Substituting for ![]() in the equilibrium equations, rearranging, and taking the limit as the volume of the tetrahedron goes to zero, (i.e., as
in the equilibrium equations, rearranging, and taking the limit as the volume of the tetrahedron goes to zero, (i.e., as ![]() ) lead to the linear relationship between the traction vector
) lead to the linear relationship between the traction vector ![]() and the unit normal vector
and the unit normal vector ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{pmatrix} t_{n1} \\ t_{n2} \\ t_{n3} \\ \end{pmatrix} = \begin{pmatrix} \sigma_{11} & \sigma_{21} & \sigma_{31} \\ \sigma_{12} & \sigma_{22} & \sigma_{32} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} \\ \end{pmatrix} \begin{pmatrix} n_1 \\ n_2 \\ n_3 \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f87ee73a892b05e448918c647bd9fcfc_l3.png)
Therefore:
![]()
I.e., the Cauchy stress tensor ![]() is a linear operator that acts as a linear function from
is a linear operator that acts as a linear function from ![]() such that
such that ![]() where
where ![]() is a unit vector, the result
is a unit vector, the result ![]() is the traction vector (force vector per unit area) acting on the surface with normal
is the traction vector (force vector per unit area) acting on the surface with normal ![]() .
.
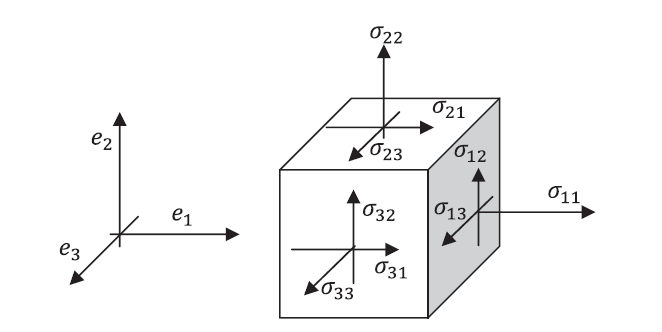
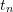 on the inclined face. (c) Areas of the different faces.
on the inclined face. (c) Areas of the different faces.Symmetry of the Stress Matrix
Because of moment equilibrium whether the body is in static or dynamic equilibrium, it will be shown that in common materials, the Cauchy Stress Tensor is a symmetric tensor, i.e., ![]() . According to Euler’s laws of motion, the rate of change of the angular momentum
. According to Euler’s laws of motion, the rate of change of the angular momentum ![]() in the material is equal to the moment of the external forces. Euler’s laws can be applied to an
infinitesimal cuboid with external forces acting on its faces as shown in Figure 4. The moment around the axis perpendicular to the plane shown and passing through the bottom left corner (black dot), neglecting smaller quantities, can be evaluated as follows:
in the material is equal to the moment of the external forces. Euler’s laws can be applied to an
infinitesimal cuboid with external forces acting on its faces as shown in Figure 4. The moment around the axis perpendicular to the plane shown and passing through the bottom left corner (black dot), neglecting smaller quantities, can be evaluated as follows:
![]()
Assuming the cuboid rotates around the bottom left corner with angular velocity ![]() , then
, then ![]() has the following form:
has the following form:
![]()
where ![]() is the density,
is the density, ![]() is the angular acceleration and I is the polar moment of inertia. Equating
is the angular acceleration and I is the polar moment of inertia. Equating ![]() with
with ![]() and taking the limit as the volume goes to zero(
and taking the limit as the volume goes to zero(![]() ,
,![]() ):
):
![]()
Similarly, ![]() and
and ![]() . Therefore:
. Therefore:
![]()
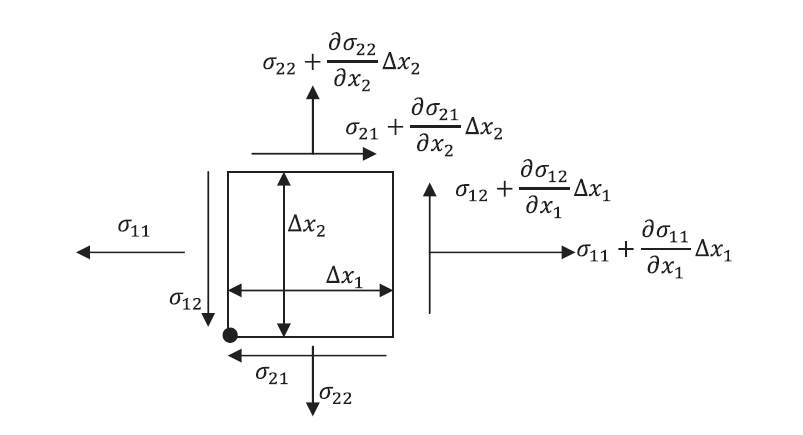
 of an infinitesimal cuboid with dimensions
of an infinitesimal cuboid with dimensions  ,
,  , and
, and 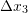 .
.Normal and Shear Stress
Given a state of stress described by ![]() and given a plane with perpendicular
and given a plane with perpendicular ![]() , the normal stress
, the normal stress ![]() is a real number representing the component of the force acting perpendicular to that plane and is given by (positive for tension and negative for compression):
is a real number representing the component of the force acting perpendicular to that plane and is given by (positive for tension and negative for compression):
![]()
While the shear stress ![]() is the magnitude of the component of the traction vector acting parallel to the surface of the plane:
is the magnitude of the component of the traction vector acting parallel to the surface of the plane:
![]()
Two Dimensional Illustrative Example
In this example a two dimensional state of stress at a point is described by the Cauchy stress tensor ![]() . Consider a plane with normal
. Consider a plane with normal ![]() . The black arrow in the figure below indicates the direction of the plane, the traction vector
. The black arrow in the figure below indicates the direction of the plane, the traction vector ![]() is indicated by the blue arrow, the green arrow (outwards indicate tension and inwards indicate compression) shows the normal stress while the red arrow indicates the direction of the shear stress vector. The values are given next to the table. Try it out by changing the values in the boxes below and hitting enter (Notice that the vector n is normalized before any computations are performed):
is indicated by the blue arrow, the green arrow (outwards indicate tension and inwards indicate compression) shows the normal stress while the red arrow indicates the direction of the shear stress vector. The values are given next to the table. Try it out by changing the values in the boxes below and hitting enter (Notice that the vector n is normalized before any computations are performed):
Try to answer the following questions:
Find a state of stress and a direction when the green arrow is pointing opposite to the black arrow. What happens to the directions of the other vectors?
Find a state of stress and a direction such that the normal stress is zero while the shear stress is not and vice versa. What happens to the stress state when you change
 in each case?
in each case? What happens when you choose n to be horizontal or vertical?
What happens when you choose values for the stress components such that
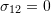 and
and 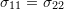 ?
?
Three Dimensional Illustrative Example
Now try to answer the same questions on the three dimensional example below by changing the values in the box and hitting enter:
Principal Stresses and Principal Directions
Since ![]() is symmetric, there exists a coordinate system in which the component form of
is symmetric, there exists a coordinate system in which the component form of ![]() is diagonal, i.e., there is a coordinate transformation such that the planes perpendicular to the coordinate system have no shear stresses! This coordinate system is the one aligned with the eigenvectors of the stress tensor. The eigenvectors are called “The Principal Directions” while the eigenvalues are called “The Principal Stresses”.
is diagonal, i.e., there is a coordinate transformation such that the planes perpendicular to the coordinate system have no shear stresses! This coordinate system is the one aligned with the eigenvectors of the stress tensor. The eigenvectors are called “The Principal Directions” while the eigenvalues are called “The Principal Stresses”.
The principal stresses are denoted ![]() ,
, ![]() and
and ![]() . If
. If ![]() ,
, ![]() and
and ![]() are the corresponding normalized eigenvectors, then
are the corresponding normalized eigenvectors, then
![Rendered by QuickLaTeX.com \[Q = \begin{pmatrix} ev_{11} & ev_{12} & ev_{13} \\ ev_{21} & ev_{22} & ev_{23} \\ ev_{31} & ev_{32} & ev_{33} \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b681f4ab22c32eb6386ab3226450ca8d_l3.png)
is an orthogonal matrix of transformation into the coordinate system described by the eigenvectors. The order of the eigenvectors should be chosen to preserve the right hand orientation of the new coordinate system and in this case ![]() is a rotation. The stress matrix in this particular coordinate system will be diagonal:
is a rotation. The stress matrix in this particular coordinate system will be diagonal:
![Rendered by QuickLaTeX.com \[\sigma ' = Q\sigma Q^T = \begin{pmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \\ \end{pmatrix}\]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-135232b87a5dbbbc5476371e7e870046_l3.png)
Two Dimensional Illustrative Example
Consider a two dimensional state of stress at a point described by the Cauchy stress tensor ![]() . The square on the left in the figure below is aligned with the original coordinate system. The red and blue arrows represent the traction vectors acting on the horizontal and vertical planes, respectively. The example below finds the eigenvalues and eigenvectors of the stress matrix. Then, a coordinate transformation described by the matrix
. The square on the left in the figure below is aligned with the original coordinate system. The red and blue arrows represent the traction vectors acting on the horizontal and vertical planes, respectively. The example below finds the eigenvalues and eigenvectors of the stress matrix. Then, a coordinate transformation described by the matrix ![]() whose rows represent the eigenvectors of
whose rows represent the eigenvectors of ![]() is used to rotate everything into that new coordinate system. In the new coordinate system, the force vectors are perpendicular to the faces of the square!
is used to rotate everything into that new coordinate system. In the new coordinate system, the force vectors are perpendicular to the faces of the square!
Three Dimensional Illustrative Example
Similarly, the example below illustrates the concept of rotating a cube into the coordinate system described by the eigenvectors of ![]() . The sizes of the arrows showing the traction or principal stress vectors qualitatively represent the magnitudes of the vectors. I.e they are not proportionate to the magnitude but only represent which vector has the larger or smaller magnitude relative to others.
. The sizes of the arrows showing the traction or principal stress vectors qualitatively represent the magnitudes of the vectors. I.e they are not proportionate to the magnitude but only represent which vector has the larger or smaller magnitude relative to others.
Mohr’s Circle for Plane Stress
Visit Wikipedia’s entry on Mohr Circle to learn about the history, the construction and the applications of Mohr’s circle!
In the following example, you can change the values of the stress matrix entries from -10 to 10 units to reconstruct Mohr’s circle. The black arrow indicates the point on the circle corresponding to a plane oriented at an angle (theta) with respect to the dotted line which corresponds to the plane perpendicular to the horizontal direction. The angle on the circle between the dotted and solid arrows is (2theta).

thanks for this useful paper it is the best in this subject
Thanks for the best subject … this is very usefull .. I have some query about three D coordinate transformation
Dear University of Alberta
What a great page. This is a very important topic and this page makes it look simple.
Thank you so much for caring for the students who need this!!!!!