The Principle of Virtual Work: Illustrative Examples for the Principle of Virtual Work
Learning Outcomes
- Describe the different expressions that appear in the statement of virtual work in a continuum.
- Describe the different expressions that appear in the statement of virtual work in an Euler Bernoulli beam.
Example 1: Illustrative Example of the Principle of Virtual Work Applied to a Continuum
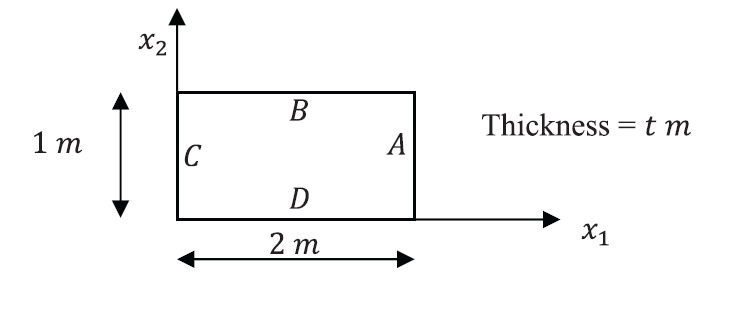
The Cauchy stress distribution in the shown plate is given by:
![Rendered by QuickLaTeX.com \[ \sigma=\left(\begin{matrix}x_1x_2&5&0\\5&x_1&0\\0&0&0\end{matrix}\right)KN/m^2 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-b25f71d5914413237cbddd7cd56478ff_l3.png)
where ![]() and
and ![]() are the coordinates inside the plate with units of
are the coordinates inside the plate with units of ![]() . Find the equilibrium body forces vector applied to the plate. Find the traction forces on the boundary edges
. Find the equilibrium body forces vector applied to the plate. Find the traction forces on the boundary edges ![]() ,
, ![]() ,
, ![]() , and
, and ![]() of the plate. Verify the principle of virtual work assuming a virtual displacement field
of the plate. Verify the principle of virtual work assuming a virtual displacement field ![]() .
.
SOLUTION:
The equilibrium body forces applied to the plate can be obtained using the equilibrium equations:
![Rendered by QuickLaTeX.com \[\begin{split} \rho b_1 & =-\frac{\partial \sigma_{11}}{\partial x_1}-\frac{\partial \sigma_{21}}{\partial x_2}-\frac{\partial \sigma_{31}}{\partial x_3}=-x_2\\ \rho b_2 & =-\frac{\partial \sigma_{12}}{\partial x_1}-\frac{\partial \sigma_{22}}{\partial x_2}-\frac{\partial \sigma_{32}}{\partial x_3}=0\\ \rho b_3 & =-\frac{\partial \sigma_{13}}{\partial x_1}-\frac{\partial \sigma_{23}}{\partial x_2}-\frac{\partial \sigma_{33}}{\partial x_3}=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d6eeb6b7f57216db39b9464230fd5b08_l3.png)
The plate is in a state of plane stress, so, the problem can be reduced to ![]() . The area vectors for the boundary edges
. The area vectors for the boundary edges ![]() , and
, and ![]() are given by:
are given by:
![]()
The traction vectors in units of ![]() on the boundary edges
on the boundary edges ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are given by:
are given by:
![]()
Therefore,
![]()
The virtual displacement vector is:
![]()
The gradient of the virtual displacement tensor is:
![]()
The associated virtual strain is given by:
![]()
The internal virtual work can be calculated as follows:
![Rendered by QuickLaTeX.com \[ IVW=\int_0^t \int_0^1 \int_0^2 \! \sum_{i,j=1}^3\sigma_{ij}\varepsilon_{ij}^*\,\mathrm{d}x_1\mathrm{d}x_2\mathrm{d}x_3=\int_0^t \int_0^1 \int_0^2 \! 5b+ax_1x_2\,\mathrm{d}x_1\mathrm{d}x_2\mathrm{d}x_3=(a+10b)t \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-88b910ba5303f91fcc540997c82255f3_l3.png)
There are five components for the external virtual work. The first one is the external virtual work due to the external body forces applied to the plate. This component is a volume integral:
![Rendered by QuickLaTeX.com \[\begin{split} EVW|_{\mbox{Body Forces}}&=\int_0^t \int_0^1 \int_0^2 \! \sum_{i}^3\rho b_i u_i^* \,\mathrm{d}x_1\mathrm{d}x_2\mathrm{d}x_3\\ &=\int_0^t \int_0^1 \int_0^2 \! -x_2(ax_1+bx_2)\,\mathrm{d}x_1\mathrm{d}x_2\mathrm{d}x_3\\ &=-\frac{1}{3}(3a+2b)t \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c945f033b29ef29d54a1ff6b6fa3f51e_l3.png)
The second component is the external virtual work due to the external forces acting on side ![]() . This is a surface integral and is evaluated for side
. This is a surface integral and is evaluated for side ![]() where
where ![]() :
:
![]()
The third component is the external virtual work due to the external forces acting on side ![]() . This is a surface integral and is evaluated for side
. This is a surface integral and is evaluated for side ![]() where
where ![]() :
:
![]()
The fourth component is the external virtual work due to the external forces acting on side ![]() . This is a surface integral and is evaluated for side
. This is a surface integral and is evaluated for side ![]() where
where ![]() :
:
![]()
The fifth component is the external virtual work due to the external forces acting on side ![]() . This is a surface integral and is evaluated for side
. This is a surface integral and is evaluated for side ![]() where
where ![]() :
:
![]()
Therefore, the total external virtual work is:
![Rendered by QuickLaTeX.com \[\begin{split} EVW & =EVW_{\mbox{Body Forces}}+EVW_A+EVW_B+EVW_C+EVW_D\\ & =-\frac{1}{3}(3a+2b)t+2\left(a+\frac{b}{3}\right)t+10\left(a+b\right)t+0-10at\\ & =(a+10b)t\\ & =IVW \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4c951849440a7d811f0d7c833cfe6684_l3.png)
View Mathematica Code
s = {{x1*x2, 5, 0}, {5, x1, 0}, {0, 0, 0}};
x = {x1, x2, x3};
rhob1 = -Sum[D[s[[j, 1]], x[[j]]], {j, 1, 2}]
rhob2 = -Sum[D[s[[j, 2]], x[[j]]], {j, 1, 2}]
rhob3 = -Sum[D[s[[j, 3]], x[[j]]], {j, 1, 2}]
(*We will only consider the 2 dimensional matrices as all out of plane components are equal to 0*)
ustar = {a*x1 + b*x2, 0};
ustara = ustar /. x1 -> 2;
ustarb = ustar /. x2 -> 1;
ustarc = ustar /. x1 -> 0;
ustard = ustar /. x2 -> 0;
s = {{x1*x2, 5}, {5, x1}};
na = {1, 0};
nb = {0, 1};
nc = {-1, 0};
nd = {0, -1};
ta = s . na /. x1 -> 2
tb = s . nb /. x2 -> 1
tc = s . nc /. x1 -> 0
td = s . nd /. x2 -> 0
Gradustar = Table[D[ustar[[i]], x[[j]]], {i, 1, 2}, {j, 1, 2}]
estar = 1/2*(Gradustar + Transpose[Gradustar])
ststrain = Sum[s[[i, j]]*estar[[i, j]], {i, 1, 2}, {j, 1, 2}]
IVW = Integrate[ststrain, {x1, 0, 2}, {x2, 0, 1}, {x3, 0, t}]
EVWBodyForces =
Integrate[rhob1*ustar[[1]], {x1, 0, 2}, {x2, 0, 1}, {x3, 0, t}]
EVWa = Integrate[(ta . ustara) /. x1 -> 2, {x2, 0, 1}, {x3, 0, t}]
EVWb = Integrate[(tb . ustarb) /. x2 -> 1, {x1, 0, 2}, {x3, 0, t}]
EVWc = Integrate[(tc . ustarc) /. x1 -> 0, {x2, 0, 1}, {x3, 0, t}]
EVWd = Integrate[(td . ustard) /. x2 -> 0, {x1, 0, 2}, {x3, 0, t}]
EVW = FullSimplify[EVWBodyForces + EVWa + EVWb + EVWc + EVWd]
View PythonCode
import sympy as sp
from sympy import Matrix, diff, integrate, simplify
x1,x2,x3 = sp.symbols("x_1 x_2 x_3")
s = Matrix([[x1*x2,5,0],[5,x1,0],[0,0,0]])
x = Matrix([[x1,x2,x3]])
pb1,pb2,pb3 =[-sum([diff(s[i,j],x[i]) for i in range(3)]) for j in range(3)]
display("\u03C1b_1 =",pb1)
display("\u03C1b_2 =",pb2)
display("\u03C1b_3 =",pb3)
a,b,t = sp.symbols("a b t")
ustar = Matrix([a*x1 + b*x2, 0])
display("u* =",ustar)
gradustar = Matrix([[diff(i,j) for j in x[:2]]for i in ustar])
display("\u2207u* =",gradustar)
ustara = ustar.subs({x1:2})
ustarb = ustar.subs({x2:1})
ustarc = ustar.subs({x1:0})
ustard = ustar.subs({x2:0})
s = Matrix([[x1*x2,5],[5,x1]])
na = Matrix([1,0])
nb = Matrix([0,1])
nc = Matrix([-1,0])
nd = Matrix([0,-1])
ta = (s*na).subs({x1:2})
tb = (s*nb).subs({x2:1})
tc = (s*nc).subs({x1:0})
td = (s*nd).subs({x2:0})
display("t_A =",ta,"t_B =",tb,"t_C =",tc,"t_D =",td)
estar = sp.Rational("1/2")*(gradustar+gradustar.T)
display("\u03B5* =",estar)
ststrain = sum([s[i]*estar[i] for i in range(4)])
display("ststrain =",ststrain)
IVW = integrate(ststrain,(x1,0,2),(x2,0,1),(x3,0,t))
display("Internal Virtual Work =",IVW)
EVWBodyForces = integrate(pb1*ustar[0],(x1,0,2),(x2,0,1),(x3,0,t))
display("External Virtual Work|_{Body Forces} =",EVWBodyForces)
EVWa = integrate((ta.dot(ustara)).subs({x1:2}),(x2,0,1),(x3,0,t))
display("External Virtual Work|_A =",EVWa)
EVWb = integrate((tb.dot(ustarb)).subs({x2:1}),(x1,0,2),(x3,0,t))
display("External Virtual Work|_B =",EVWb)
EVWc = integrate((tc.dot(ustarc)).subs({x1:0}),(x2,0,1),(x3,0,t))
display("External Virtual Work|_C =",EVWc)
EVWd = integrate((td.dot(ustard)).subs({x2:0}),(x1,0,2),(x3,0,t))
display("External Virtual Work|_D =",EVWd)
EVW = simplify(EVWBodyForces+EVWa+EVWb+EVWc+EVWd)
display("External Virtual Work = Internal Virtual Work =",EVW)
Video
Example 2: Illustrative Example of the Principle of Virtual Work Applied to an Euler Bernoulli Beam
A fixed ends Euler Bernoulli beam is subjected to a distributed load ![]() . Assuming that Young’s modulus, the length, and the moment of inertia for the beam are
. Assuming that Young’s modulus, the length, and the moment of inertia for the beam are ![]() ,
, ![]() , and
, and ![]() , respectively, verify that the principle of virtual work applies when a virtual parabolic displacement
, respectively, verify that the principle of virtual work applies when a virtual parabolic displacement ![]() ,
, ![]() is applied to the beam.
is applied to the beam.
SOLUTION:
The principle of virtual work applies to the equilibrium internal forces. So, the first step is to find the internal forces at the state of equilibrium. For this, we will solve the differential equation of equilibrium:
![]()
The integration constants ![]() ,
, ![]() ,
, ![]() , and
, and ![]() can be obtained using the four boundary conditions of a fixed ends beam:
can be obtained using the four boundary conditions of a fixed ends beam:
![Rendered by QuickLaTeX.com \[\begin{split} @X_1=0:y=0\\ @X_1=0:\theta=y'=0\\ @X_1=L:y=0\\ @X_1=L:\theta=y'=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-640cc8056e88504f8d237e6b3a330a24_l3.png)
Therefore, the equilibrium displacement of the beam is:
![]()
The bending moment and the shearing force equations at equilibrium are:
![Rendered by QuickLaTeX.com \[\begin{split} M& =EI\frac{\mathrm{d}^2y}{\mathrm{d}X_1^2}=\frac{1}{12}(-2L^3+9L^2X_1-10X_1^3)\\ V& =EI\frac{\mathrm{d}^3y}{\mathrm{d}X_1^3}=\frac{3}{4}L^2-\frac{5}{2}X_1^2 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-873eefd8df05f04dcf48880491e47912_l3.png)
The external forces acting on the ends of the beam are given by:
![]()
Note that the convention for positive end forces is shown in Figure 3. The virtual end displacements and rotations are given by:
![]()
Therefore, the internal virtual work is given by:
![]()
The external virtual work has three components, the first is the external virtual work due to the distributed load q:
![]()
The second component is the external virtual work due to the reactions at end 1:
![]()
The third component is the external virtual work due to the reactions at end 2:
![]()
The total external virtual work is:
![]()
View Mathematica Code
Clear[M, y, EI, x, s]
q = -5 x
s = DSolve[{EI*y''''[x] == q, y[0] == 0, y'[0] == 0, y[L] == 0,
y'[L] == 0}, y[x], x]
y = y[x] /. s[[1]]
th = D[y, x]
M = FullSimplify[EI*D[y, {x, 2}]]
V = FullSimplify[EI*D[y, {x, 3}]]
M1 = M /. x -> 0
M2 = M /. x -> L
V1 = V /. x -> 0
V2 = V /. x -> L
ystar = a*x^2;
thstar = D[ystar, x];
ystar1 = ystar /. x -> 0
ystar2 = ystar /. x -> L
thstar1 = thstar /. x -> 0
thstar2 = thstar /. x -> L
Print["IVW"]
IVW = Integrate[M*D[ystar, {x, 2}], {x, 0, L}]
EVWq = Integrate[q*ystar, {x, 0, L}]
EVW1 = +V1*ystar1 - M1*thstar1
EVW2 = -V2*ystar2 + M2*thstar2
Print["EVW"]
EVW = EVWq + EVW1 + EVW2
View Python Code
import sympy as sp
from sympy import Function,dsolve,diff,simplify,integrate
x,EI,L = sp.symbols("x EI L")
y = Function("y")
a = sp.symbols("a")
y1 = y(x).subs(x,0)
y2 = y(x).subs(x,L)
yp1 = y(x).diff(x).subs(x,0)
yp2 = y(x).diff(x).subs(x,L)
q = -5*x
s = dsolve(EI*y(x).diff(x,4)-q,y(x),ics={y1:0,y2:0,yp1:0,yp2:0})
y = s.rhs
display("y(x) =",y)
th = simplify(diff(y,x))
M = simplify(EI*diff(y,x,x))
V = simplify(EI*diff(y,x,x,x))
display("th =",th,"M =",M,"V =",V)
M1 = M.subs({x:0})
M2 = M.subs({x:L})
V1 = V.subs({x:0})
V2 = V.subs({x:L})
display("M@x=0",M1,"M@x=L",M2,"V@x=0",V1,"V@x=L",V2)
ystar = a*x**2
thstar = diff(ystar,x)
ystar1 = ystar.subs({x:0})
ystar2 = ystar.subs({x:L})
thstar1 = thstar.subs({x:0})
thstar2 = thstar.subs({x:L})
display("y*@x=0",ystar1,"y*@x=L",ystar2,"\u03B8*@x=0",thstar1,"\u03B8*@x=L",thstar2)
IVW = integrate(M*diff(ystar,x,x),(x,0,L))
display("Internal Virtual Work =",IVW)
EVWq = integrate(q*ystar,(x,0,L))
display("EVWq =",EVWq)
EVW1 = V1*ystar1-M1*thstar1
EVW2 = M2*thstar2-V2*ystar2
display("EVW1 =",EVW1,"EVW2 =",EVW2)
EVW = EVWq+EVW1+EVW2
display("External Virtual Work = Internal Virtual Work =",EVW)
Video
Example 3: Application 1 of the Principle of Virtual Work
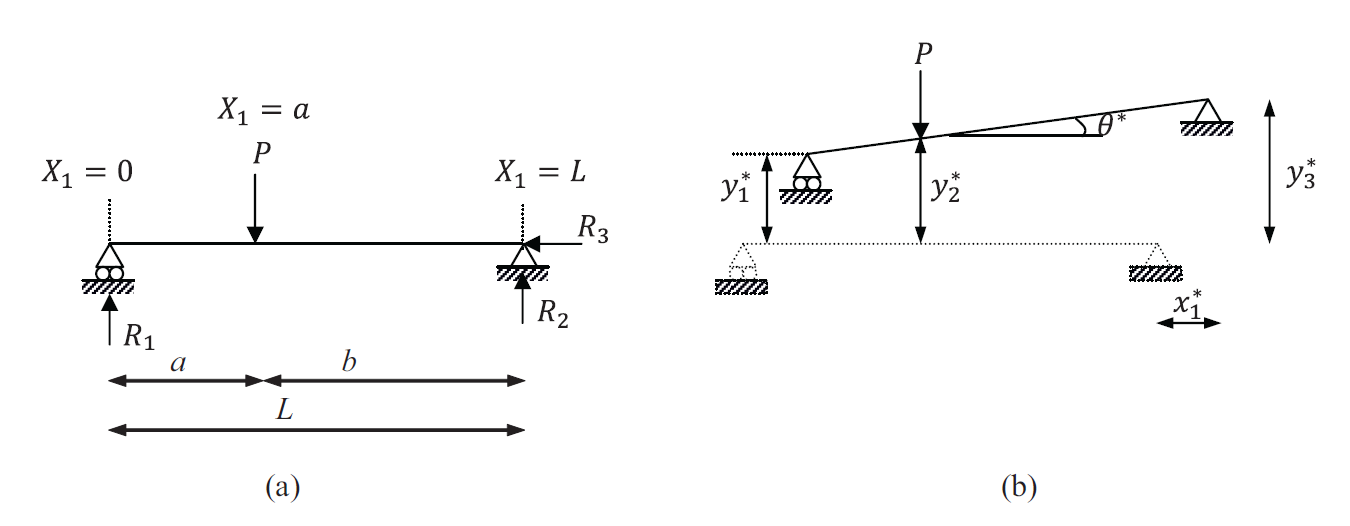
The shown beam has its neutral axis aligned with the ![]() axis. Find the reactions
axis. Find the reactions ![]() ,
, ![]() , and
, and ![]() using the equilibrium equations and then using the principle of virtual work.
using the equilibrium equations and then using the principle of virtual work.
SOLUTION:
There are three equilibrium equations which can be used to find the three unknown reactions:
![]()
Therefore, the three unknown reactions are:
![]()
The principle of virtual work can be used by applying a virtual smooth rigid body displacement to the beam. The rigid body displacement will in fact have three unknown variables. Each variable will correspond to an equilibrium of motion. In this example, the virtual vertical displacement field:
![]()
and a horizontal displacement equal to ![]() . In essence, the rigid body displacement has three variables,
. In essence, the rigid body displacement has three variables, ![]() ,
, ![]() , and
, and ![]() .
. ![]() corresponds to moving the beam vertically upwards and will be used to write the equation of equilibrium that states that the sum of vertical forces is equal to zero.
corresponds to moving the beam vertically upwards and will be used to write the equation of equilibrium that states that the sum of vertical forces is equal to zero. ![]() corresponds to moving the beam horizontally and will be used to write the equation of equilibrium that states that the sum of the horizontal forces is equal to zero.
corresponds to moving the beam horizontally and will be used to write the equation of equilibrium that states that the sum of the horizontal forces is equal to zero. ![]() corresponds to rotating the beam around point 1 which will be used to write the equation of equilibrium that states that the sum of moments around point 1 is equal to zero.
corresponds to rotating the beam around point 1 which will be used to write the equation of equilibrium that states that the sum of moments around point 1 is equal to zero.
The statement of virtual work of the system is:
![]()
![]() and
and ![]() are the virtual displacements of points 2 and 3 and can be replaced with
are the virtual displacements of points 2 and 3 and can be replaced with ![]() and
and ![]() so the equation becomes:
so the equation becomes:
![]()
The above equation can be rearranged to have the following form:
![]()
Since the virtual displacement field is arbitrary and the statement applies for any choices of the variables ![]() , and
, and ![]() , then, their coefficients are equal to zero. Therefore, the three equations of equilibrium are retrieved:
, then, their coefficients are equal to zero. Therefore, the three equations of equilibrium are retrieved:
![]()
Therefore, the same reactions are obtained. Note that the chosen virtual displacement field guarantees that the associated internal virtual work is equal to zero.
Video
Example 4: Application 1 of the Principle of Virtual Work
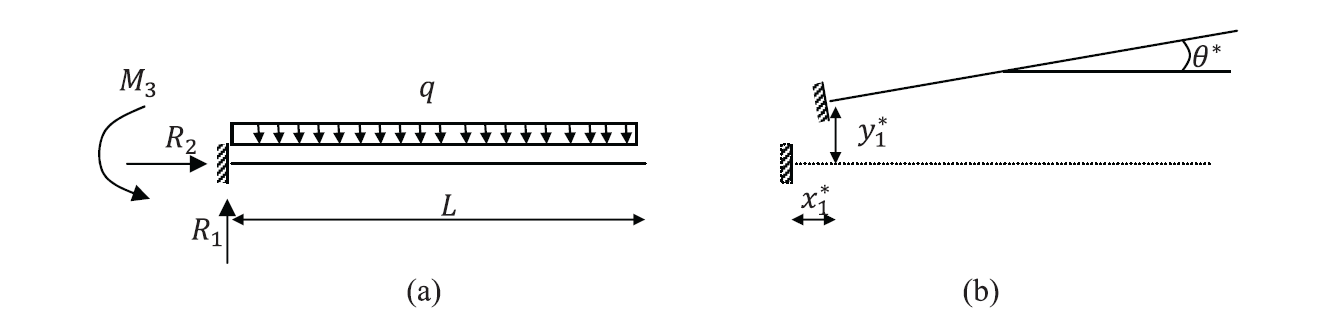
The shown beam has its neutral axis aligned with the ![]() axis. Find the reactions
axis. Find the reactions ![]() , and
, and ![]() using the equilibrium equations and then using the principle of virtual work.
using the equilibrium equations and then using the principle of virtual work.
SOLUTION:
There are three equilibrium equations which can be used to find the three unknown reactions:
![]()
Therefore, the three unknown reactions are:
![]()
The principle of virtual work can be used by applying a virtual smooth rigid body displacement to the beam. The rigid body displacement will in fact have three unknown variables. Each variable will correspond to an equilibrium of motion. In this example, the virtual vertical displacement field:
![]()
and a horizontal displacement equal to ![]() . In essence, the rigid body displacement has three variables,
. In essence, the rigid body displacement has three variables, ![]() ,
, ![]() , and
, and ![]() .
. ![]() corresponds to moving the beam vertically upwards and will be used to write the equation of equilibrium that states that the sum of vertical forces is equal to zero.
corresponds to moving the beam vertically upwards and will be used to write the equation of equilibrium that states that the sum of vertical forces is equal to zero. ![]() corresponds to moving the beam horizontally and will be used to write the equation of equilibrium that states that the sum of the horizontal forces is equal to zero.
corresponds to moving the beam horizontally and will be used to write the equation of equilibrium that states that the sum of the horizontal forces is equal to zero. ![]() corresponds to rotating the beam around point 1 which will be used to write the equation of equilibrium that states that the sum of moments around point 1 is equal to zero.
corresponds to rotating the beam around point 1 which will be used to write the equation of equilibrium that states that the sum of moments around point 1 is equal to zero.
The statement of virtual work of the system is:
![]()
After substituting for ![]() and integrating, the above equation can be rearranged to have the following form:
and integrating, the above equation can be rearranged to have the following form:
![]()
Notice that the displacement field is chosen small enough such that ![]() . The above equation can then be rearranged to have the following form:
. The above equation can then be rearranged to have the following form:
![]()
Since the virtual displacement field is arbitrary and the statement applies for any choices of the variables ![]() ,
, ![]() , and
, and ![]() , then, their coefficients are equal to zero. Therefore, the three equations of equilibrium are retrieved:
, then, their coefficients are equal to zero. Therefore, the three equations of equilibrium are retrieved:
![]()
Therefore, the same reactions are obtained. Note that the chosen virtual displacement field guarantees that the associated internal virtual work is equal to zero.
Example 5: Application 2 of the Principle of Virtual Work
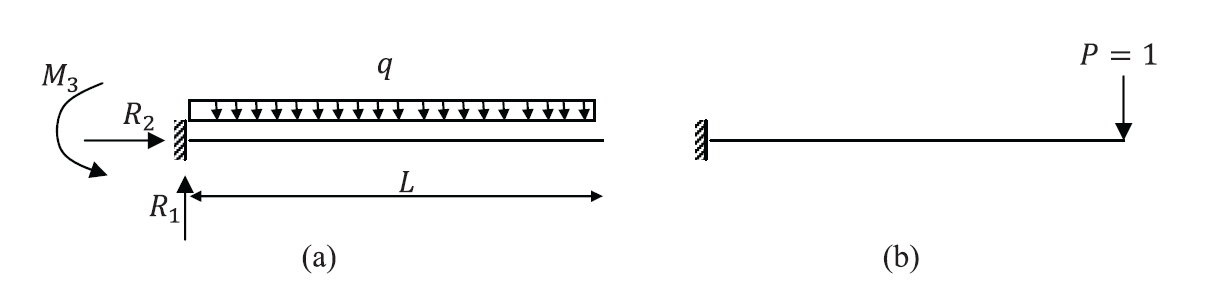
Use the principle of virtual work to find the displacement at the free end of the shown cantilever beam. Assume EI is constant and ignore the shearing force and normal force deformations.
SOLUTION:
The bending moment of the structure with the original load (distributed load) is given by the equation:
![]()
After removing the loads from the structure and applying a unit load at the point of interest, the bending moment equation for the structure with the unit load ![]() is given by the equation:
is given by the equation:
![]()
Applying the statement of virtual work as described above for this application:
![]()
Therefore:
![]()
Example 6: Application 3 of the principle of Virtual Work
Use the principle of virtual work to find an approximate cubic polynomial displacement solution for the shown beam. Compare with the exact solution for ![]() unit and
unit and ![]() unit where
unit where ![]() and
and ![]() are the Young’s modulus, beam’s length, and moment of inertia respectively. Ignore Poisson’s ratio.
are the Young’s modulus, beam’s length, and moment of inertia respectively. Ignore Poisson’s ratio.
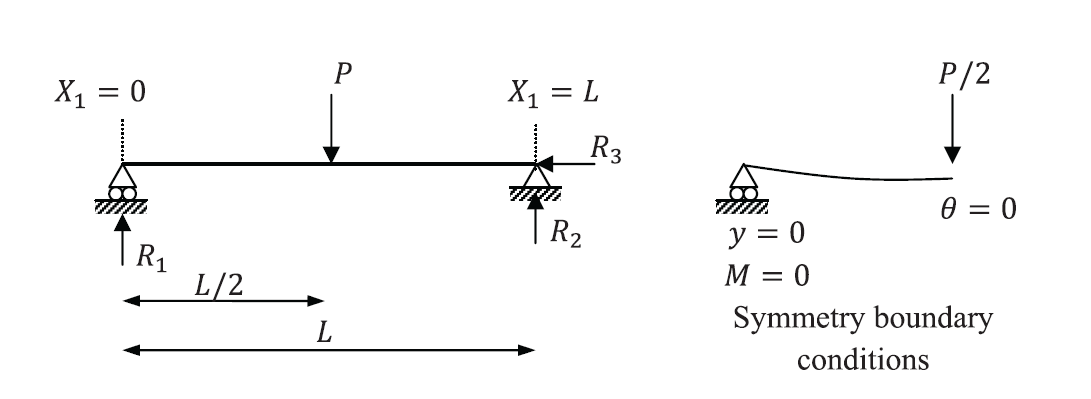
SOLUTION:
First, we will find the exact displacement shape by solving the differential equation of equilibrium. Because of symmetry, we are going to solve the equation for only half the beam with the boundary conditions shown in the figure.
![]()
The constants ![]() , and
, and ![]() are integration constants and can be obtained from the four boundary conditions:
are integration constants and can be obtained from the four boundary conditions:
![Rendered by QuickLaTeX.com \[\begin{split} @X_1=0:y=0\\ @X_1=0:M=EI\frac{\mathrm{d}^2y}{\mathrm{d}X_1^2}=0\\ @X_1=\frac{L}{2}:V=EI\frac{\mathrm{d}^3y}{\mathrm{d}X_1^3}=\frac{P}{2}\\ @X_1=\frac{L}{2}:\theta=\frac{\mathrm{d}y}{\mathrm{d}X_1}=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8a3c8c53129edf04dd719698d0027eff_l3.png)
Therefore, the displacement function ![]() for
for ![]() is given by:
is given by:
![]()
The displacement function for ![]() can be obtained by replacing
can be obtained by replacing ![]() with
with ![]() in
in ![]() and thus the final displacement shape has the form:
and thus the final displacement shape has the form:
![]()
The following are two important observations about the exact solution:
- The exact solution is a polynomial of the third degree for each half.
We wish now to find an approximate solution for the displacement. We will force the solution however, to be continuous and differentiable at ![]() by assuming that the approximate solution is a cubic function applied from the whole length of the beam:
by assuming that the approximate solution is a cubic function applied from the whole length of the beam:
![]()
The first step in finding the appropriate coefficients ![]() , and
, and ![]() is to ensure that this approximate solution satisfies the boundary conditions of displacement and rotation if any. Therefore we need to ensure:
is to ensure that this approximate solution satisfies the boundary conditions of displacement and rotation if any. Therefore we need to ensure:
![]()
Therefore,
![]()
Thus, the approximate displacement shape that would satisfy the boundary conditions has the form:
![]()
The associated bending moment diagram in this case has the following form:
![]()
In order to apply the principle of virtual work, a virtual displacement needs to be assumed. Since the principle of virtual work applies for any assume virtual displacement, the most general virtual displacement field within the space of possible functions will be assumed. Since we restricted the solutions to be quadratic functions satisfying the boundary conditions, the most general virtual displacement has the form:
![]()
and the associated second derivative has the form:
![]()
The internal virtual work can be calculated as follows:
![Rendered by QuickLaTeX.com \[\begin{split} IVW & =\int_0^L \! EI\frac{\mathrm{d}^2y_{approx}}{\mathrm{d}X_1^2}\frac{\mathrm{d}^2y^*}{\mathrm{d}X_1^2}\,\mathrm{d}X_1=\int_0^L \! EI(2a_2+6a_3X_1)(2a_2^*+6a_3^*X_1)\,\mathrm{d}X_1\\ & =EI (4a_2La_2^* + 6a_3L^2 a_2^*+6a_2L^2a_3^*+12a_3L^3a_3^*)\\ & = EI(4a_2L+6a_3L^2)a_2^* + EI(6a_2L^2+12a_3L^3)a_3^* \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a2122b95bde873cc48e394d34bb4401e_l3.png)
On the other hand, the external virtual work has only one component due to the virtual work done by the force ![]() as the virtual displacement at the reactions is equal to zero:
as the virtual displacement at the reactions is equal to zero:
![]()
Since the principle of virtual applies to any choice for ![]() and
and ![]() , their multipliers on both sides of the equation of virtual work have to be equal. Therefore, we get the following two equations:
, their multipliers on both sides of the equation of virtual work have to be equal. Therefore, we get the following two equations:
![]()
Solving the above two equations yields:
![]()
Therefore, the best approximate solution that satisfies the virtual work principle is;
![]()
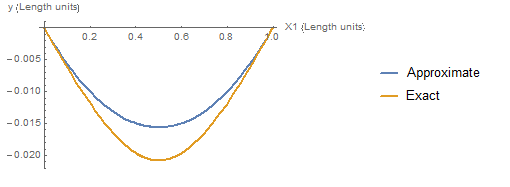
The approximate solution can be compared with the exact solution when ![]() units. The plot of
units. The plot of ![]() versus
versus ![]() shows that the approximate solution under-predicts the displacement of the structure. In other words, the approximate solution gives a stiffer structure compared to the exact solution.
shows that the approximate solution under-predicts the displacement of the structure. In other words, the approximate solution gives a stiffer structure compared to the exact solution.
View Mathematica Code
Clear[y, P, X1, EI, L, yexact];
(*Exact solution*)
s = DSolve[{y''''[X1] == 0, y[0] == 0, y''[0] == 0, y'[L/2] == 0,
y'''[L/2] == P/2/EI}, y[X1], X1];
y1 = FullSimplify[y[X1] /. s[[1]]];
y2 = FullSimplify[y1 /. X1 -> L - X1];
yexact = Piecewise[{{y1, 0 <= X1 < L/2}, {y2, L/2 <= X1 <= L}}];
(*Approximate solution*)
yapprox = a2*X1*(X1 - L) + a3*X1*(X1^2 - L^2);
ystar = yapprox /. {a2 -> a2s, a3 -> a3s};
EVW = -P*ystar /. X1 -> L/2;
IVW = Integrate[EI*D[yapprox, {X1, 2}]*D[ystar, {X1, 2}], {X1, 0, L}];
Eq1 = Coefficient[IVW, a2s] - Coefficient[EVW, a2s];
Eq2 = Coefficient[IVW, a3s] - Coefficient[EVW, a3s];
s = Solve[{Eq1 == 0, Eq2 == 0}, {a2, a3}];
yapprox = yapprox /. s[[1]];
yp = yapprox /. {P -> 1, EI -> 1, L -> 1};
yexactp = yexact /. {P -> 1, EI -> 1, L -> 1};
Plot[{yp, yexactp}, {X1, 0, 1},
PlotLegends -> {"Approximate", "Exact"},
AxesLabel -> {"X1 (Length units)", "y (Length units)"}]
View Python Code
from sympy import Function,dsolve,diff,integrate,Poly,solve,simplify
import numpy as np
import matplotlib.pyplot as plt
y = Function("y")
x,EI,L,P = sp.symbols("x EI L P")
a2,a3,a2s,a3s = sp.symbols("a_2 a_3 a_2s a_3s")
y1 = y(x).subs({x:0})
th2 = y(x).diff(x).subs(x,L/2)
M1 = y(x).diff(x,2).subs(x,0)
V2 = y(x).diff(x,3).subs(x,L/2)
s = dsolve(y(x).diff(x,4),y(x),ics={y1:0,th2:0,M1:0,V2:P/2/EI})
y1 = s.rhs
y2 = simplify(y1.subs({x:L-x}))
yapprox = a2*x*(x-L)+a3*x*(x**2-L**2)
ystar = yapprox.subs({a2:a2s,a3:a3s})
EVW = (-P*ystar).subs({x:L/2}).expand()
IVW = integrate(EI*diff(yapprox,x,x)*diff(ystar,x,x),(x,0,L)).expand()
Eq1 = IVW.coeff(a2s)-EVW.coeff(a2s)
Eq2 = IVW.coeff(a3s)-EVW.coeff(a3s)
s = solve({Eq1,Eq2},{a2,a3})
yapprox = yapprox.subs({a2:s[a2],a3:s[a3]})
y1exactp = y1.subs({L:1,EI:1,P:1})
y2exactp = y2.subs({L:1,EI:1,P:1})
yp = yapprox.subs({L:1,EI:1,P:1})
xL = xrange = np.arange(0,1.01,0.01)
Y1 = []
Y2 = []
for i in range(len(xL)):
Y1.append(yp.subs({x:xL[i]}))
#piecewise for exact : y1 when 0<=x<L/2, y2 when L/2=<x<L
if i<(len(xL)/2):
Y2.append(y1exactp.subs({x:xL[i]}))
else:
Y2.append(y2exactp.subs({x:xL[i]}))
fig, ax = plt.subplots()
plt.xlabel("x(length units)")
plt.ylabel("y(length units)")
ax.plot(xL, Y1, label="Approx")
ax.plot(xL, Y2, label="Exact")
ax.legend()
ax.grid(True, which='both')
ax.axhline(y = 0, color = 'k')
ax.axvline(x = 0, color = 'k')
Video
Problems
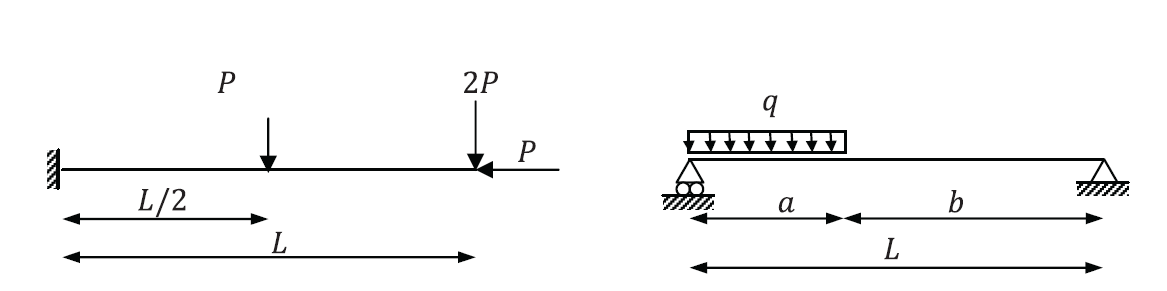
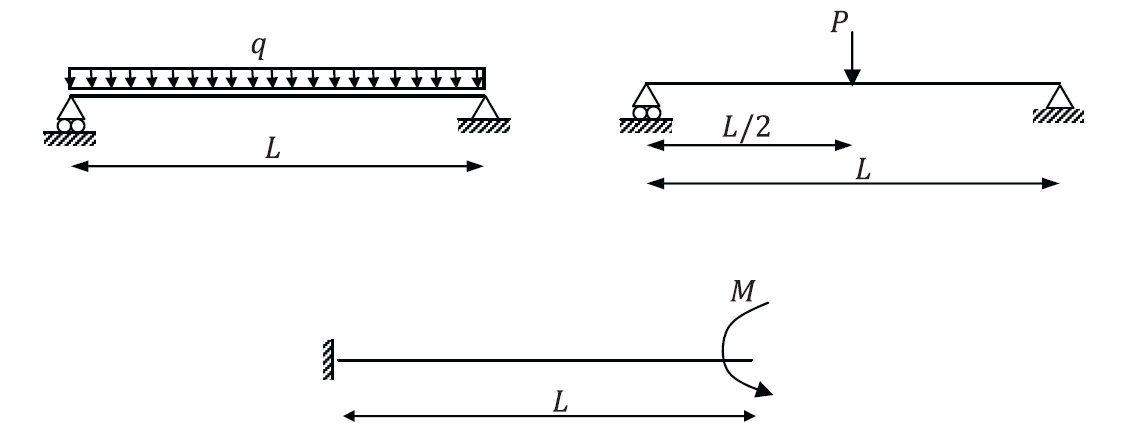
- Use the principle of virtual work to find the reactions for the following statically determinate structures.
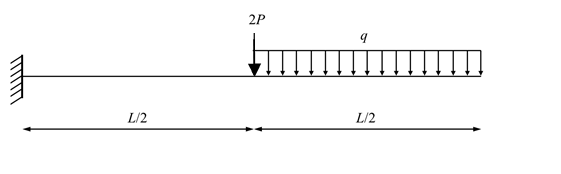
- Use the principle of virtual work to find the reactions for the following statically determinate structures.
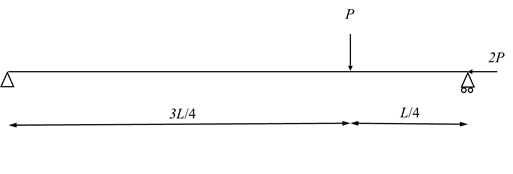
- The shown beams have Young’s modulus
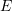 and moment of inertia
and moment of inertia 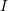 . Verify that the virtual work principle applies assuming a virtual displacement field
. Verify that the virtual work principle applies assuming a virtual displacement field  where
where 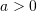 .
.
- Repeat the previous question assuming a virtual displacement field
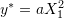 where
where 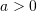 .
.
- The Cauchy stress distribution in the shown plate is given by:
where![Rendered by QuickLaTeX.com \[ \sigma=\left(\begin{matrix}x_1&3&0\\3&0&0\\0&0&0\end{matrix}\right)KN/m^2 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-06ce9e531aaabcacd63b50bb19ff8ac6_l3.png)
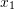 and
and  are the coordinates inside the plate with units of m. Find the equilibrium body forces vector applied to the plate. Find the traction forces on the boundary edges
are the coordinates inside the plate with units of m. Find the equilibrium body forces vector applied to the plate. Find the traction forces on the boundary edges 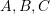 , and
, and 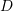 of the plate. Verify the principle of virtual work in the following two cases:
of the plate. Verify the principle of virtual work in the following two cases:
- Assuming a virtual displacement field
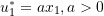 .
. - Assuming a virtual displacement field
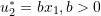 .
.

- Assuming a virtual displacement field
- The Cauchy stress distribution on the shown unit length cube is given by:
where![Rendered by QuickLaTeX.com \[ \sigma=\left(\begin{matrix}x_1x_2&4&2\\4&x_1&0\\2&0&x_3\end{matrix}\right)KN/m^2 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cb9909f9d280d7d71c37fb2aad5e3919_l3.png)
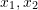 , and
, and 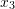 are the coordinates inside the cube with units of
are the coordinates inside the cube with units of 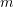 .
.
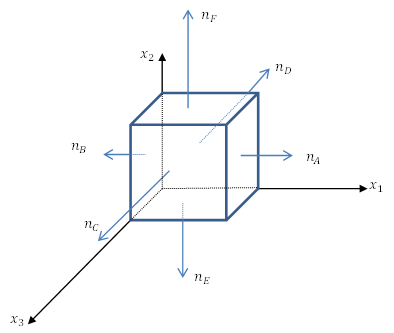
- Find the equilibrium body forces vector applied on the cube.
- Find the traction vectors on the boundary faces
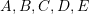 , and
, and 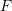 of the cube.
of the cube. - Verify the principle of virtual work for the following virtual displacement field
where![Rendered by QuickLaTeX.com \[ u^*=\left(\begin{matrix}ax_1\\bx_2\\cx_3\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9bad634732c055853faeea5eb3336d80_l3.png)
 , and
, and  are positive real numbers.
are positive real numbers.
- Use the principle of virtual work to find approximate linear, quadratic, cubic, and quartic polynomial displacement solutions for a simply supported beam with length
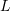 , Young’s modulus
, Young’s modulus 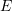 , moment of inertia
, moment of inertia 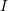 , and a distributed load
, and a distributed load 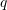 . Compare the approximate solutions with the exact solution for
. Compare the approximate solutions with the exact solution for 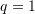 units,
units, 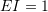 units, and
units, and 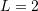 units. Ignore Poisson’s ratio.
units. Ignore Poisson’s ratio.
