Open Educational Resources

Calculus: Matrix Calculus

In this section, we show some useful formulas that are used in the derivation of the forms of the stress matrices of hyperelastic materials.

Statement 1

Let F\in\mathbb{M}^3 be a deformation gradient satisfying J=\det(F)>0. Let U^2=F^TF be the square of the right stretch tensor of the polar decomposition of the deformation gradient. Let I_1(U^2) and I_2(U^2) be the first and second invariants of U^2 respectively, which for simplicity, will be denoted by I_1 and I_2. Then:

    \[ \begin{split} &\frac{\partial I_1}{\partial F}=2F\\ &\frac{\partial I_2}{\partial F}=2I_1F-2FF^TF\\ &\frac{\partial J}{\partial F}=JF^{-T} \end{split} \]

Note that the first two equalities hold for any matrix A\in\mathbb{M}^3. The last formula is referred to as the Jacobi formula.

PROOF:

For the first statement, we start by noting that the first invariant of U^2 can be written using the components of F as follows:

    \[ I_1(U^2)=I_1(F^TF)=\sum_{k,l=1}^3 F_{kl}F_{kl}=F_{kl}F_{kl} \]

By taking the derivative of I_1 with respect to the arbitrary component F_{ij} we get:

    \[ \frac{\partial I_1}{\partial F_{ij}}=2F_{kl}\frac{\partial F_{kl}}{\partial F_{ij}} = 2F_{kl}(\delta_{ki}\delta_{lj})=2F_{ij} \]

Therefore,

    \[ \frac{\partial I_1}{\partial F}=2F \]

The second inequality can be obtained similarly, by writing I_2(U^2) in terms of the components of F:

    \[ I_2(U^2)=\frac{1}{2}\left(\left(I_1\left(U^2\right)\right)^2-I_1 \left(U^4 \right)\right)=\frac{1}{2}\left(\left(I_1\left(F^TF\right)\right)^2-I_1 \left(F^TFF^TF \right)\right) \]

Therefore:

    \[ \frac{\partial I_2}{\partial F}=I_1(F^TF) \frac{\partial I_1}{\partial F}- \frac{1}{2}\frac{\partial I_1(F^TFF^TF)}{\partial F} \]

The second term can be evaluated using component form as follows:

    \[\begin{split} \frac{\partial I_1(F^TFF^TF)}{\partial F_{ij}}&=\frac{\partial F_{kn}F_{kl}F_{ml}F_{mn})}{\partial F_{ij}}=F_{il} F_{ml} F_{mj}+F_{in} F_{mj} F_{mn}+F_{kn} F_{kj} F_{in}+F_{kj} F_{kl} F_{il}\\ &=4F_{ik} F_{lk} F_{lj} \end{split} \]

i.e.,

    \[ \frac{\partial I_1(F^TFF^TF)}{\partial F}=4FF^TF \]

Therefore, the derivative of the second invariant of U^2 has the following form:

    \[ \frac{\partial I_2}{\partial F}=2I_1(F^TF) F-2FF^TF \]

The Jacobi formula can be shown by first writing the expression of the determinant of a matrix in component form as follows:

    \[ J=\varepsilon_{ijk}F_{1i}F_{2j}F_{3k} \]

If F is invertible, which is the case when F represents a deformation gradient, then it is enough to show the following equivalent form of the Jacobi formula:

    \[\frac{\partial J}{\partial F}F^T=J I \]

To prove the above, we start by the left hand side in component form:

    \[ \begin{split} \left(\frac{\partial J}{\partial F}F^T\right)_{nm}&=\frac{\partial J}{\partial F_{no}}F_{mo}=\frac{\partial \varepsilon_{ijk}F_{1i}F_{2j}F_{3k}}{\partial F_{no}}F_{mo}\\ &=(\varepsilon_{ijk} \delta_{1n} \delta_{io} F_{2j} F_{3k} ) F_{mo}+(\varepsilon_{ijk} F_{1i} \delta_{2n} \delta_{jo} F_{3k} ) F_{mo}+(\varepsilon_{ijk} F_{1i} F_{2j} \delta_{3n} \delta_{ko} ) F_{mo}\\ &=\varepsilon_{ojk} F_{mo} F_{2j} F_{3k} \delta_{1n}+\varepsilon_{iok} F_{1i} F_{mo} F_{3k} \delta_{2n}+\varepsilon_{ijo} F_{1i} F_{2j} F_{mo} \delta_{3n} \end{split} \]

Each term of the above equation represents the triple product of three row vectors in F. Since the triple product of linearly dependent vectors is zero, the three terms can be rewritten as follows:

    \[ \begin{split} &\varepsilon_{ojk}F_{mo}F_{2j}F_{3k}=\varepsilon_{ojk}F_{1o}F_{2j}F_{3k}\delta_{1m}\\ &\varepsilon_{iok}F_{1i}F_{mo}F_{3k}=\varepsilon_{iok}F_{1i}F_{2o}F_{3k}\delta_{2m}\\ &\varepsilon_{ijo}F_{1i}F_{2j}F_{mo}=\varepsilon_{ijo}F_{1i}F_{2j}F_{3o}\delta_{3m} \end{split} \]

Substituting in the above equation leads to:

    \[ \begin{split} \left(\frac{\partial J}{\partial F}F^T\right)_{nm}&=\varepsilon_{ojk}F_{1o}F_{2j}F_{3k}\delta_{1m}+\varepsilon_{iok}F_{1i}F_{2o}F_{3k}\delta_{2m}+\varepsilon_{ijo}F_{1i}F_{2j}F_{30}\delta_{3m}\\ &=\varepsilon_{ijk}F_{1i}F_{2j}F_{3k}(\delta_{1n}\delta_{m1}+\delta_{2n}\delta_{m2}+\delta_{3n}\delta_{m3})\\ &=\varepsilon_{ijk}F_{1i}F_{2j}F_{3k}(\delta_{nm})\\ &=J\delta_{nm} \end{split} \]

Therefore,

    \[ \frac{\partial J}{\partial F}F^T=J I\Rightarrow \frac{\partial J}{\partial F}=JF^{-T} \]

Statement 2 (Component Form)

Let F\in\mathbb{M}^3 be a deformation gradient satisfying J=\det(F)>0. Let U^2=F^TF be the square of the right stretch tensor of the polar decomposition of the deformation gradient. Let F=RQDQ^T be the singular value decomposition of the deformation gradient where R,Q\in\mathbb{M}^3 are rotation matrices, the columns of Q are the eigenvectors of U^2 and D\in\mathbb{M}^3 is a diagonal matrix with entries:

    \[ D=\left(\begin{array}{ccc} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_3 \end{array} \right) \]

Then:

    \[ \begin{split} &\frac{\partial \lambda_1}{\partial F_{ij}}=\sum_{k=1}^3Q_{k1}R_{ik}Q_{j1}\\ &\frac{\partial \lambda_2}{\partial F_{ij}}=\sum_{k=1}^3Q_{k2}R_{ik}Q_{j2}\\ &\frac{\partial \lambda_3}{\partial F_{ij}}=\sum_{k=1}^3Q_{k3}R_{ik}Q_{j3} \end{split} \]

PROOF:

Rearranging the singular value decomposition equality:

    \[ D=\left(\begin{array}{ccc} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_3 \end{array} \right)=Q^TR^TFQ \]

Therefore, using component form we have:

    \[ \begin{split} &\lambda_1=\sum_{k,l,m=1}^3Q_{k1}R_{lk}F_{lm}Q_{m1}\\ &\lambda_2=\sum_{k,l,m=1}^3Q_{k2}R_{lk}F_{lm}Q_{m2}\\ &\lambda_2=\sum_{k,l,m=1}^3Q_{k3}R_{lk}F_{lm}Q_{m3} \end{split} \]

By taking the derivatives with respect to the general component F_{ij}:

    \[ \frac{\partial \lambda_1}{\partial F_{ij}}=\frac{\partial \left(\sum_{k,l,m=1}^3Q_{k1}R_{lk}F_{lm}Q_{m1}\right)}{\partial F_{ij}}=\sum_{k,l,m=1}^3Q_{k1}R_{lk}F_{lm}Q_{m1}\delta_{li}\delta_{mj}=\sum_{k=1}^3Q_{k1}R_{ik}Q_{j1} \]

Similarly,

    \[ \begin{split} &\frac{\partial \lambda_2}{\partial F_{ij}}=\sum_{k=1}^3Q_{k2}R_{ik}Q_{j2}\\ &\frac{\partial \lambda_3}{\partial F_{ij}}=\sum_{k=1}^3Q_{k3}R_{ik}Q_{j3} \end{split} \]

Statement 2 (Tensor Form):

In the previous statement, the derivatives of the eigenvectors with respect to the components of F were shown to be functions of the components of Q and R. Since the columns of Q are the eigenvectors of U^2 then the derivatives are functions of the components of the eigenvectors. The complexity of the component form hides the simplicity of the actual relationship and so the tensor product form will be used to show how simple the relationship actually is. In addition, we are going to also show the simple relationship of the derivatives of the eigenvectors of U with respect to the tensor C as follows:

Let C=F^TF be the Right Cauchy-Green Deformation Tensor and B=FF^T be the Left Cauchy-Green Deformation Tensor. Let \lambda_1^2, \lambda_2^2 and \lambda_3^2 be the eigenvalues of C and B. Let N_1, N_2, and N_3 be the eigenvectors of C and n_1, n_2, and n_3 be the eigenvectors of B. Show that \forall i\in\{1,2,3\} (no summation):

    \[ \frac{\partial \lambda_i}{\partial C}=\frac{1}{2\lambda_i}(N_i\otimes N_i) \]

    \[ \frac{\partial \lambda_i}{\partial F}=(n_i\otimes N_i) \]

PROOF:

First, assume that f is a scalar valued function of C. Therefore:

    \[ f(C)=f(\lambda_1^2 N_1\otimes N_1+\lambda_2^2 N_2\otimes N_2 + \lambda_3^2 N_3\otimes N_3) \]

By taking the derivative of f with respect to C, we get the second order tensor:

    \[ \frac{\partial f}{\partial C}=\sum_{i=1}^3\left(\frac{\partial f}{\partial \lambda_i^2}N_i\otimes N_i +\lambda_i^2\frac{\partial f}{\partial (N_i\otimes N_i)}\right) \]

Setting f=\sqrt{\lambda_1^2} we have:

    \[ \frac{\partial f}{\partial \lambda_1^2}=\frac{1}{2\lambda_1} \]

Since the eigenvalues of C are independent of each other and of the eigenvectors, we have:

    \[ \frac{\partial f}{\partial \lambda_2^2}=\frac{\partial f}{\partial \lambda_3^2}=\frac{\partial f}{\partial (N_1\otimes N_1)}=\frac{\partial f}{\partial (N_2\otimes N_2)}=\frac{\partial f}{\partial (N_3\otimes N_3)}=0 \]

Therefore:

    \[ \frac{\partial \lambda_1}{\partial C}=\frac{1}{2\lambda_1}(N_1\otimes N_1) \]

The same statement applies for f=\sqrt{\lambda_2^2} and f=\sqrt{\lambda_3^2}. Therefore \forall i\in\{1,2,3\}:

    \[ \frac{\partial \lambda_i}{\partial C}=\frac{1}{2\lambda_i}(N_i\otimes N_i) \]

The same proof can be used to show that \forall i\in\{1,2,3\}:

    \[ \frac{\partial \lambda_i}{\partial F}=n_i\otimes N_i \]

Equivalence of the Component and Tensor Forms of Statement 2:

Note that since the columns of Q in the statement above are the eigenvectors of U^2, (N_i)_j=Q_{ji}. Also, we have (n_i)_j=(RN_i)_j=\sum_{k=1}^3R_{jk}(N_i)_k=\sum_{k=1}^3R_{jk}Q_{ki}. Also, (n_i\otimes N_i)_{jk}=(n_i)_j(N_i)_k. Therefore:

    \[ \frac{\partial \lambda_1}{\partial F_{ij}}=(n_1\otimes N_1)_{ij}=\sum_{k=1}^3Q_{k1}R_{ik}Q_{j1} \]

which is the component form obtained above.

Statement 3:

Let F\in\mathbb{M}^3 be a deformation gradient satisfying J=\det(F)>0. Let U^2=F^TF be the square of the right stretch tensor of the polar decomposition of the deformation gradient. Let \overline{F}=J^{-\frac{1}{3}}F. Let \overline{I_1},\overline{I_2} be the first and second invariants of \overline{F^T}\overline{F} respectively.
Then:

    \[ \begin{split} &\frac{\partial \overline{I_1}}{\partial F}=J^{-\frac{2}{3}}\left(2F-\frac{2I_1}{3}F^{-T}\right)\\ &\frac{\partial \overline{I_2}}{\partial F}=J^{-\frac{4}{3}}\left(2I_1F-2FF^TF-\frac{4I_2}{3}F^{-T}\right) \end{split} \]

Where I_1,I_2 are the first and second invariants of F^TF respectively.

PROOF:

From the properties of the first invariant of a matrix:

    \[ \overline{I_1} \left(\overline{F^T}\overline{F}\right)=\overline{I_1} \left(J^{-\frac{2}{3}}F^TF\right)=J^{-\frac{2}{3}}I_1 \]

Therefore:

    \[ \frac{\partial \overline{I_1}}{F}=\frac{\partial \overline{I_1}}{I_1}\frac{\partial I_1}{F}+\frac{\partial \overline{I_1}}{J}\frac{\partial \overline{J}}{F}=J^{-\frac{2}{3}}2F-\frac{2I_1}{3}J^{-\frac{5}{3}}(JF^{-T})=J^{-\frac{2}{3}}\left(2F-\frac{2I_1}{3}F^{-T}\right) \]

Similarly:

    \[ \overline{I_2} \left(\overline{F^T}\overline{F}\right)=\frac{1}{2}\left(\left(\overline{I_1}\left(\overline{F^T}\overline{F}\right)\right)^2-\overline{I_1}\left(\overline{F^T}\overline{F}\overline{F^T}\overline{F}\right) \right)=J^{-\frac{4}{3}}I_2\left(F^TF\right) \]

Therefore:

    \[\begin{split} \frac{\partial \overline{I_2}}{F}&=\frac{\partial \overline{I_2}}{I_2}\frac{\partial I_2}{F}+\frac{\partial \overline{I_2}}{J}\frac{\partial \overline{J}}{F}=J^{-\frac{4}{3}}(2I_1F-2FF^TF)-\frac{4I_2}{3}J^{-\frac{7}{3}}(JF^{-T})\\ &=J^{-\frac{4}{3}}\left(2I_1F-2FF^TF-\frac{4I_2}{3}F^{-T}\right) \end{split} \]

Statement 4:

Let F\in\mathbb{M}^3 be a deformation gradient satisfying J=\det(F)>0. Assume the components of F are functions of a variable \alpha\in\mathbb{R}, then:

    \[ \frac{\partial J}{\partial \alpha}=J \mbox{Trace}\left(\frac{\partial F}{\partial \alpha}F^{-1}\right) \]

NOTES:
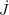  • If the variable \alpha represents time, then the relationship between \dot{J} and the trace of the velocity gradient 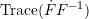\mbox{Trace}(\dot{F}F^{-1}) is obtained (see this section).
  • While the statement is intended for a matrix whose determinant is positive, a more general statement applicable to a square-matrix valued function, “Jacobi’s formula”, can be derived in a similar fashion.
PROOF:

The section on the velocity gradient provides two proofs for the particular relationship between the velocity gradient and \dot{J}. These two are based on the books by Ogden and P. Chadwich. The two approaches are repeated here for a general parameters \alpha.

The first approach relies on the component form in a cartesian coordinate system. J can be expressed in terms of the components of F as follows:

    \[ J=\sum_{i,j,k=1}^3\varepsilon_{ijk}\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k} \]

Then, by taking the time derivatives, the following expression for the derivative of J is obtained:

    \[ \frac{\partial J}{\partial \alpha} = \sum_{i,j,k=1}^3\varepsilon_{ijk}\left(\frac{\partial \frac{\partial x_1}{\partial \alpha}}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k}+\frac{\partial x_1}{\partial X_i}\frac{\partial \frac{\partial x_2}{\partial \alpha}}{\partial X_j}\frac{\partial x_3}{\partial X_k}+\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial \frac{\partial x_3}{\partial \alpha}}{\partial X_k}\right) \]

The following relationship will be used to replace some of the expressions in the derivative of J:

    \[ \frac{\partial \frac{\partial x_k}{\partial \alpha}}{\partial X_l}=\sum_{i=1}^3\frac{\partial \frac{\partial x_k}{\partial \alpha}}{\partial x_i}\frac{\partial x_i}{\partial X_l} \]

Additionally, from the properties of the determinant, the following expressions which are equal to zero for any values of a,b\leq 3 will be used:

    \[ \sum_{i,j,k=1}^3\varepsilon_{ijk}\frac{\partial x_a}{\partial X_i}\frac{\partial x_a}{\partial X_j}\frac{\partial x_b}{\partial X_k}=\sum_{i,j,k=1}^3\varepsilon_{ijk}\frac{\partial x_a}{\partial X_i}\frac{\partial x_b}{\partial X_j}\frac{\partial x_b}{\partial X_k}=\sum_{i,j,k=1}^3\varepsilon_{ijk}\frac{\partial x_a}{\partial X_i}\frac{\partial x_b}{\partial X_j}\frac{\partial x_a}{\partial X_k}=0 \]

Substituting in the derivative of J results in the following expression:

    \[ \begin{split} \frac{\partial J}{\partial \alpha} & = \sum_{i,j,k=1}^3\varepsilon_{ijk}\left(\frac{\partial \frac{\partial x_1}{\partial \alpha}}{\partial x_1}\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k}+\frac{\partial \frac{\partial x_2}{\partial \alpha}}{\partial x_2}\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k}+\frac{\partial \frac{\partial x_3}{\partial \alpha}}{\partial x_3}\frac{\partial x_1}{\partial X_i}\frac{\partial x_2}{\partial X_j}\frac{\partial x_3}{\partial X_k}\right)\\ &=J\sum_{i=1}^3\left(\frac{\partial\frac{\partial x_i}{\partial \alpha}}{\partial x_i}\right)=J\sum_{i,j=1}^3\frac{\frac{\partial x_i}{\partial \alpha}}{\partial X_j}\frac{\partial X_j}{\partial x_i} \end{split} \]

which is the desired expression in component form.

The second approach is adopted from the book by P. Chadwich and relies on the expressions shown in the matrix invariants section. Let a,b,c\in\mathbb{R}^3 be three linearly independent vectors. The derivative of J can be expressed as follows:

    \[ \begin{split} \frac{\partial J}{\partial \alpha} &=\frac{\frac{\partial F}{\partial\alpha}a\cdot(Fb\times Fc)+Fa\cdot(\frac{\partial F}{\partial\alpha}b\times Fc)+Fa\cdot(Fb\times \frac{\partial F}{\partial\alpha}c)}{a\cdot(b\times c)}\\ &=\frac{\frac{\partial F}{\partial\alpha}F^{-1}Fa\cdot(Fb\times Fc)+Fa\cdot(\frac{\partial F}{\partial\alpha}F^{-1}Fb\times Fc)+Fa\cdot(Fb\times \frac{\partial F}{\partial\alpha}F^{-1}Fc)}{a\cdot(b\times c)}\\ &=\frac{\frac{\partial F}{\partial\alpha}F^{-1}Fa\cdot(Fb\times Fc)+Fa\cdot(\frac{\partial F}{\partial\alpha}F^{-1}Fb\times Fc)+Fa\cdot(Fb\times \frac{\partial F}{\partial\alpha}F^{-1}Fc)}{Fa\cdot(Fb\times Fc)}\frac{Fa\cdot(Fb\times Fc)}{a\cdot(b\times c)}\\ &=J \mbox{Trace}\left(\frac{\partial F}{\partial\alpha}F^{-1}\right) \end{split} \]

Leave a Reply

Your email address will not be published.