Open Educational Resources

Approximate Methods: The Rayleigh Ritz Method: Bars Under Axial Loads

Learning Outcomes

  • Describe the steps required to find an approximate solution for a beam system using the Rayleigh Ritz method. (Step1: Assume a displacement function, apply the BC. Step 2: Write the expression for the PE of the system. Step 3: Find the minimizers of the PE of the system.)
  • Employ the RR method to compute an approximate solution for the displacement in a beam under axial load.
  • Differentiate between the requirement for an approximate solution and an exact solution.

The Rayleigh Ritz method is a classical approximate method to find the displacement function of an object such that the it is in equilibrium with the externally applied loads. It is regarded as an ancestor of the widely used Finite Element Method (FEM). The Rayleigh Ritz method relies on the principle of minimum potential energy for conservative systems. The method involves assuming a form or a shape for the unknown displacement functions, and thus, the displacement functions would have a few unknown parameters. These assumed shape functions are termed Trial Functions. Afterwards, the potential energy function of the system is written in terms of those few parameters, and the values of those parameters that would minimize the potential energy function of the system are calculated. Mathematically speaking, we assume that the unknown displacement function u is a member of a certain space of functions; for example, we can assume that u\in V where V is the set of all the possible vector valued linear functions defined on the body represented by the set \Omega_0\subset \mathbb{R}^3:V=\{u:\Omega_0\rightarrow \mathbb{R}^3|\forall x\in\Omega_0:u(x)=Bx, B\in\mathbb{M}^3\}. With this assumption, we restrict the possible solutions to those in the form u=Bx, and thus, the unknown parameters are restricted to the matrix B, which in this particular example, has nine components. Finally, the nine components that would minimize the potential-energy function are obtained. The method will be illustrated using various one-dimensional examples.

Bars Under Axial Loads

The Rayleigh Ritz method seeks to find an approximate solution to minimize the potential energy of the system. For plane bars under axial loading, the unknown displacement function is u_1. In this case, the potential energy of the system has the following form (See beams under axial loads and energy expressions):

    \[PE = Total \hspace{1mm} Strain \hspace{1mm} Energy - W = \int \frac{EA}{2} (\frac{du_1}{dX_1})^2 dX_1 - W\]

where E is Young’s modulus, A is the cross sectional area, and W is the work done by all the external forces acting on the bar (concentrated forces and distributed loads). To obtain an approximate solution for u_1, a trial function of a finite number of unknowns is first selected. Then, this trial function has to satisfy the “essential” boundary conditions, which are those boundary conditions that would satisfy the physical stability of the system. In the case of bars under axial loads, the trial function u_1 has to satisfy the displacement boundary conditions. The following examples show the method for different external loads, and bar configurations.

Example 1: A Bar Under Axial Forces

Let a bar with a length L and a constant cross sectional area A be aligned with the coordinate axis X_1. Assume that the bar is subjected to a horizontal body force (in the direction of the axis X_1) p=CX_1 units of force/unit length where C is a known constant. Also, assume that the bar has a constant force of value P applied at the end X_1 = L. If the bar is fixed at the end X_1 = 0, find the displacement of the bar by directly solving the differential equation of equilibrium. Also, find the displacement function using the Rayleigh Ritz method assuming a polynomial function for the displacement of the degrees (0, 1, 2, 3, and 4). Assume that the bar is linear elastic with Young’s modulus E and that the small strain tensor is the appropriate measure of strain. Ignore the effect of Poisson’s ratio.

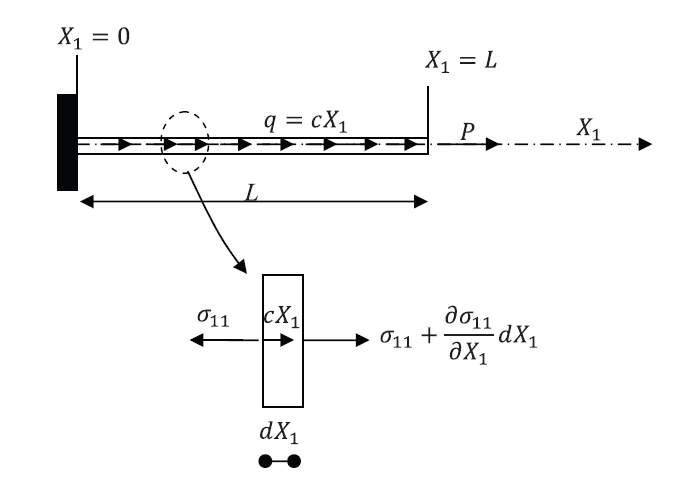
Solution

Exact Solution

First, the exact solution that would satisfy the equilibrium equations can be obtained. The equilibrium equation as shown in the beams under axial loading section when E and A are constant is:

    \[\frac{d^2u_1}{dX_1^2} = -\frac{CX_1}{EA}\]

Therefore, the exact solution has the form:

    \[u_1 = -\frac{CX_1^3}{6EA} + C_1X_1 + C_2\]

where C_1 and C_2 can be obtained from the boundary conditions:

    \[@X_1 = 0: u_1 = 0 \Rightarrow C_2 = 0\]

    \[@X_1 = L: \sigma_{11} = E\frac{du_1}{dX_1} = \frac{P}{A} \Rightarrow C_1 = \frac{P}{AE} + \frac{CL^2}{2EA}\]

Therefore, the exact solution for the displacement u_1 and the stress \sigma_{11} are:

    \[u_1 = -\frac{CX_1^3}{6EA} + (\frac{P}{AE} + \frac{CL^2}{2EA})X_1\]

    \[\sigma_{11} = E\frac{du_1}{dX_1} = -\frac{CX_1^2}{2A} + (\frac{P}{A} + \frac{CL^2}{2A})\]

View Mathematica Code

Clear[u, x]
a = DSolve[{u''[x] == -c*x/(Ee*A), u'[L] == P/(Ee*A), u[0] == 0}, u, x]
u = u[x] /. a[[1]]
FullSimplify[u]
sigma = Ee*D[u, x];
FullSimplify[sigma]

View Python Code

from sympy import *
import sympy as sp 
sp.init_printing(use_latex = "mathjax")
x, A, E , C, L, P = symbols("x A E C L P")
u = Function("u")
u1 = u(x).subs(x,0)
u2 = u(x).diff(x).subs(x,L)
a = dsolve(u(x).diff(x,2) + C*x/(E*A), u(x), ics = {u1:0, u2:P/(E*A)})
u = a.rhs
sigma = E * u.diff(x)
display("displacement and stress: ", u, simplify(sigma))

The Rayleigh Ritz Method:
The first step in the Rayleigh Ritz method finds the minimizer of the potential energy of the system which can be written as:

    \[PE = \int \overline{U} dX - W = \int_0^L \frac{\sigma_{11} \varepsilon_{11}}{2} A dX_1 - Pu_1\Big|_{X_1=L} - \int_0^L pu_1 dX_1\]

Notice that the potential energy lost by the action of the end force P is equal to the product of P and the displacement u_1 evaluated at X_1= L while the potential energy lost by the action of the distributed body forces is an integral since it acts on each point along the beam length. Further, we will use the constitutive equation to rewrite the potential energy function in terms of the function u_1:

    \[PE = \int_0^L \frac{EA}{2} \Big(\frac{du_1}{dX_1}\Big)^2 dX_1 - Pu_1\Big|_{X_1=L} - \int_0^L CX_1u_1dX_1\]

To find an approximate solution, an assumption for the shape or the form of u_1 has to be introduced.

Polynomial of the Zero Degree:
First, we can assume that u_1 is a constant function (a polynomial of the zero degree):

    \[u_1 = a_0\]

However, to satisfy the “essential” boundary condition that u_1 = 0 when X_1 = 0, the constant a_0 has to equal to zero; this leads to the trivial solution u_1= 0, which will automatically be rejected.

Polynomial of the First Degree:
As a more refined approximation, we can assume that u_1 is a linear function (a polynomial of the first degree):

    \[u_1 = a_0 + a_1X_1\]

To satisfy the essential boundary condition @X_1=0:u_1=0 the coefficient a_0 is equal to zero. Therefore:

    \[u_1 = a_1X_1\]

The strain component \varepsilon_{11} can be computed as follows:

    \[\varepsilon_{11} = \frac{du_1}{dX_1} = a_1\]

Substituting into the equation for the potential energy of the system:

    \[PE = \int_0^L \frac{EA}{2} a_1^2 dX_1 - Pa_1L - \int_0^L CX_1a_1X_1dX_1 = \frac{EAL}{2}a_1^2 - Pa_1L-\frac{Ca_1L^3}{3}\]

The only variable that can be controlled to minimize the potential energy of the system is a_1. Therefore:

    \[\frac{dPE}{da_1} = 0 \Rightarrow EAa_1L - PL - \frac{CL^3}{3} = 0 \Rightarrow a_1 = \frac{P+\frac{CL^2}{3}}{EA}\]

Therefore, the best linear function according to the Rayleigh Ritz method is:

    \[u_1 = \Big(\frac{P + \frac{CL^2}{3}}{EA}\Big)X_1\]

A linear displacement would produce a constant stress:

    \[\sigma_{11} = \Big(\frac{P + \frac{CL^2}{3}}{A}\Big)\]

Unfortunately, this solution is far from being accurate, since it does not satisfy the differential equation of equilibrium (Why?). However, within the only possible or allowed linear shapes, the obtained solution is the minimizer of the potential energy.

Polynomial of the Second Degree:
As a more refined approximation, we can assume that u_1 is a polynomial of the second degree:

    \[ u_1 = a_0+a_1 X_1+a_2X_1^2 \]

To satisfy the essential boundary condition @X_1=0:u_1=0 the coefficient a_0 is equal to zero. Therefore:

    \[ u_1 = a_1 X_1+a_2X_1^2 \]

The strain component \varepsilon_{11} can be computed as follows:

    \[ \varepsilon_{11}=\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=a_1+2a_2X_1 \]

Substituting into the equation for the potential energy of the system:

    \[\begin{split} PE&=\int_0^L\!\frac{EA}{2}(a_1+2a_2X_1)^2 \,\mathrm{d}X_1 - P(a_1L+a_2L^2)-\int_0^L\!C(a_1X_1^2+a_2X_1^3)\,\mathrm{d}X_1\\ & = \frac{2EAL^3}{3}a_2^2+EAL^2a_2a_1+\frac{EAL}{2}a_1^2-PL^2a_2-PLa_1-\frac{CL^4}{4}a_2-\frac{CL^3}{3}a_1 \end{split} \]

a_1 and a_2 are the variables that can be controlled to minimize the potential energy of the system. Therefore:

    \[ \frac{\partial PE}{\partial a_1}=0\Rightarrow EAL^2a_2+EALa_1-PL-\frac{CL^3}{3}=0 \]

and

    \[ \frac{\partial PE}{\partial a_2}=0\Rightarrow \frac{4EAL^3}{3}a_2+EAL^2a_1-PL^2-\frac{CL^4}{4}=0 \]

Solving the above two equations yields:

    \[ a_1=\frac{7CL^2+12P}{12EA}\qquad a_2=-\frac{CL}{4EA} \]

Therefore, the best second degree polynomial according to the Rayleigh Ritz method is:

    \[ u_1=-\frac{cL}{4EA}X_1^2+\frac{(7CL^2+12P)}{12EA}X_1 \]

A parabolic displacement would produce a linear stress:

    \[ \sigma_{11}=-\frac{cL}{2A}X_1+\frac{(7CL^2+12P)}{12A} \]

View Mathematica Code

Clear[u,x,a2,a1,Ee,A,c,P,L]
u=a2*x^2+a1*x;
PE=Integrate[(1/2)*Ee*A*D[u,x]^2,{x,0,L}]-P*(u/.x->L)-Integrate[c*x*u,{x,0,L}];
Eq1=D[PE,a2]
Eq2=D[PE,a1]
s=Solve[{Eq1==0,Eq2==0},{a2,a1}]
u=u/.s[[1]]
stress=FullSimplify[Ee*D[u,x]]

View Python Code

from sympy import *
import sympy as sp 
sp.init_printing(use_latex = "mathjax")
x, a1, a2, E, A, P, c = symbols("x a_1 a_2 E A P c")
u = a2*x**2+a1*x
uL = u.subs(x,L)
PE = integrate((1/2)*E*A*(u.diff(x)**2), (x,0,L)) - P*uL - integrate(c*x*u, (x,0,L))
display("Potential Energy: ", PE)
Eq1 = PE.diff(a2)
Eq2 = PE.diff(a1)
display("Minimize PE: ", Eq1, Eq2)
s = solve((Eq1, Eq2), (a2, a1))
display("Solve: ", s)
u = u.subs({a1:s[a1], a2:s[a2]})
display("Best second degree Polynomial(Rayleigh Ritz method): ", u)
stress = E * u.diff(x)
display("stress: ", simplify(stress))

Polynomial of the Third Degree:
Similarly, choosing a polynomial of the third degree as an approximate displacement function means:

    \[ u_1=a_0+a_1X_1+a_2X_1^2+a_3X_1^3 \]

with the following approximation for the axial strain

    \[ \varepsilon_{11}=a_1+2a_2X_1+3a_3X_1^2 \]

The essential boundary condition lead to a_0=0. The potential energy of the system has the form:

    \[ PE=\int_0^L\!\frac{EA}{2}(a_1+2a_2X_1+3a_3X_1^2)^2 \,\mathrm{d}X_1 - P(a_1L+a_2L^2+a_3L^3)-\int_0^L\!C(a_1X_1^2+a_2X_1^3+a_3X_1^4)\,\mathrm{d}X_1 \]

Clearly, the method generates a large set of equations that are difficult to solve by hand. Using Mathematica we can find the values of the constants a_1, a_2, and a_3 that would minimize the potential energy of the system:

View Mathematica Code

Clear[u,x,a2,a1,a3,Ee,A,c,P,L]
u=a3*x^3+a2*x^2+a1*x;
PE=Integrate[(1/2)*Ee*A*D[u,x]^2,{x,0,L}]-P*(u/.x->L)-Integrate[c*x*u,{x,0,L}];
Eq1=D[PE,a2]
Eq2=D[PE,a1]
Eq3=D[PE,a3]
s=Solve[{Eq1==0,Eq2==0,Eq3==0},{a2,a1,a3}]
u=u/.s[[1]]
stress=FullSimplify[Ee*D[u,x]]

View Python Code

from sympy import *
import sympy as sp 
sp.init_printing(use_latex = "mathjax")
x, a1, a2, a3, E, A, P, c = symbols("x a_1 a_2 a_3 E A P c")
u = a3*x**3+a2*x**2+a1*x
uL = u.subs(x,L)
PE = integrate((1/2)*E*A*(u.diff(x)**2), (x,0,L)) - P*uL - integrate(c*x*u, (x,0,L))
display("Potential Energy: ", PE)
Eq1 = PE.diff(a2)
Eq2 = PE.diff(a1)
Eq3 = PE.diff(a3)
display("Minimize PE: ", Eq1, Eq2, Eq3)
s = solve((Eq1, Eq2, Eq3), (a2, a1, a3))
display("Solve: ", s)
u = u.subs({a1:s[a1], a2:s[a2], a3:s[a3]})
display("Best third degree Polynomial(Rayleigh Ritz method): ", u)
stress = E * u.diff(x)
display("stress: ", simplify(stress))

Since the assumed trial function is a polynomial of the third degree, which is similar to the exact solution, the Rayleigh Ritz method is able to produce the exact solution for the displacement and the stresses:

    \[\begin{split} u_1 & =-\frac{CX_1^3}{6EA}+\left(\frac{P}{AE}+\frac{CL^2}{2EA}\right)X_1 \\ \sigma_{11}& = E\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=-\frac{CX_1^2}{2A}+\left(\frac{P}{A}+\frac{CL^2}{2A}\right) \end{split} \]

Example 2:A Bar Under Axial Forces With Varying Cross Sectional Area

Let a bar with a length 2m be aligned with the coordinate axis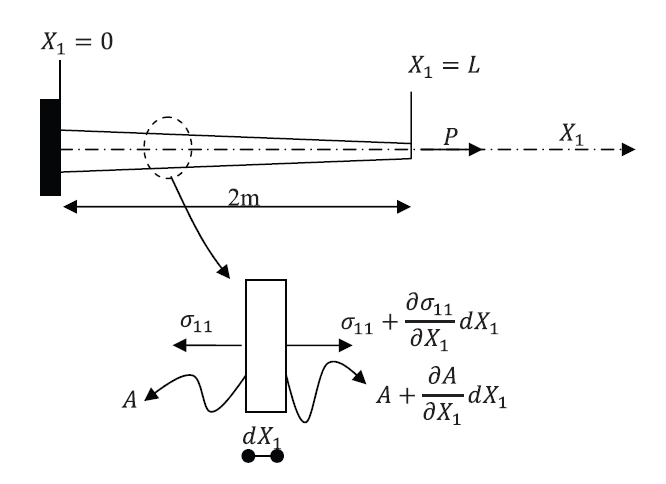 X_1, and let the width of the bar be equal to 250mm while the height varies linearly such that the height is equal to 500mm when X_1=0 and is equal to 250mm when X_1=2m. Assume that the bar has a constant force of value 200N applied at the end X_1 =2m and that the bar is fixed at the end X_1=0. Find the displacement of the bar by directly solving the differential equation of equilibrium and then using the Rayleigh Ritz method assuming a polynomials of the degrees (0, 1, 2 and 3). Assume the bar to be linear elastic with Young’s modulus E=100,000Pa and assume that the small strain tensor is the appropriate measure of strain. Ignore the effect of Poisson’s ratio. Compare the solution obtained using the Rayleigh Ritz method with the exact solution.

Solution
Exact Solution:
First, the exact solution that would satisfy the equilibrium equations can be obtained. The equilibrium equation as shown in the beams under axial loading section when E is constant and p=0 is:

    \[ EA\frac{\mathrm{d}^2u_1}{\mathrm{d}X_1^2}+E\frac{\mathrm{d}A}{\mathrm{d}X_1}\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=0 \]

The area A varies linearly with X_1 according to the equation:

    \[ A=0.25\left(0.5-\frac{0.25}{2}X_1\right) \]

The two boundary conditions are:

    \[\begin{split} @X_1=0 & :u_1=0\\ @X_1=L & :\sigma_{11}=E\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=\frac{P}{A}\bigg|_{X_1=L} \end{split} \]

Therefore, the exact solution for the displacement u_1 and the stress \sigma_{11} are:

    \[\begin{split} u_1 & =\frac{8}{125}\left(\ln{4}-\ln\left(4-X_1\right)\right)\\ \sigma_{11} & =\frac{6400}{4-X_1} \end{split} \]

Note that the exact solution for the stress could have been directly obtained by dividing the force P by the variable cross sectional area. The displacement function would then be obtained by integrating the expression \sigma_{11}=E\frac{\mathrm{d}u_1}{\mathrm{d}X_1}.

View Mathematica Code

Clear[u, x]
Ax = 25/100 (5/10 - 25/200*x);
Ee = 100000;
L = 2;
P = 200;
s = DSolve[{Ee*u''[x]*Ax + Ee*u'[x]*D[Ax, x] == 0, 
   u'[L] == 200/Ee/(Ax /. x -> L), u[0] == 0}, u, x]
u = u[x] /. s[[1]]
stress = Ee*D[u, x]

View Python Code

from sympy import *
import sympy as sp 
sp.init_printing(use_latex = "mathjax")
x, A, E , L, P = symbols("x A E L P")
u = Function("u")
u1 = u(x).subs(x,0)
u2 = u(x).diff(x).subs(x,L)
Ax = 25/100*(5/10-25/200*x)
Ax1 = Ax.subs(x,L)
display("Area: ", Ax)
s = dsolve(E*u(x).diff(x,2)*Ax+E*u(x).diff(x)*Ax.diff(x), u(x), ics = {u1:0, u2:200/E/Ax1})
u = s.rhs.subs({E:100000, L:2, P:200})
stress = (E * u.diff(x)).subs({E:100000, L:2, P:200})
display("displacement and stress: ", u, stress)

The Rayleigh Ritz Method:
The first step in the Rayleigh Ritz method finds the minimizer of the potential energy of the system which can be written as:

    \[ PE=\int\!\overline{U}\,dX - W=\int_0^L\!\frac{\sigma_{11}\varepsilon_{11}}{2}A \,\mathrm{d}X_1 - Pu_1|_{X_1=L} \]

Notice that the potential energy lost by the action of the end force P is equal to the product of P and the displacement u_1 evaluated at X_1= L. Further, we will use the constitutive equation to rewrite the potential energy function in terms of the function u_1:

    \[ PE=\int_0^L\!\frac{EA}{2}\left(\frac{\mathrm{d}u_1}{\mathrm{d}X_1}\right)^2 \,\mathrm{d}X_1 - Pu_1|_{X_1=L} \]

To find an approximate solution, an assumption for the shape or the form of u_1 has to be introduced. Similar to the previous example, a polynomial of the zero degree cannot be used as it will automatically render the displacement u_1=0.

Polynomial of the First Degree:

As a more refined approximation, we can assume that u_1 is a linear function (a polynomial of the first degree):

    \[ u_1 = a_0+a_1 X_1 \]

To satisfy the essential boundary condition @X_1=0:u_1=0 the coefficient a_0 is equal to zero. Therefore:

    \[ u_1 = a_1 X_1 \]

The strain component \varepsilon_{11} can be computed as follows:

    \[ \varepsilon_{11}=\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=a_1 \]

Substituting into the equation for the potential energy of the system:

    \[ PE=\int_0^L\!\frac{EA}{2}a_1^2 \,\mathrm{d}X_1 - Pa_1L=0.125Ea_1^2\int_0^L\!(0.5-0.125X_1) \,\mathrm{d}X_1-Pa_1L \]

The only variable that can be controlled to minimize the potential energy of the system is a_1. Therefore:

    \[ \frac{\mathrm{d}PE}{\mathrm{d}a_1}=0\Rightarrow 18750a_1=400 \]

Therefore, the best linear function (units of m) according to the Rayleigh Ritz method is:

    \[ u_1=\frac{8}{375}X_1 \]

A linear displacement would produce a constant stress (units of N/m^2):

    \[ \sigma_{11}=\frac{6400}{3} \]

Unfortunately, this solution is far from being accurate, since it does not satisfy the differential equation of equilibrium (Why?). However, within the only possible or allowed linear shapes, the obtained solution is the minimizer of the potential energy.

Polynomial of the Second Degree:
As a more refined approximation, we can assume that u_1 is a polynomial of the second degree:

    \[ u_1 = a_0+a_1 X_1+a_2X_1^2 \]

To satisfy the essential boundary condition @X_1=0:u_1=0 the coefficient a_0 is equal to zero. Therefore:

    \[ u_1 = a_1 X_1+a_2X_1^2 \]

The strain component \varepsilon_{11} can be computed as follows:

    \[ \varepsilon_{11}=\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=a_1+2a_2X_1 \]

Substituting into the equation for the potential energy of the system:

    \[\begin{split} PE&=\int_0^L\!\frac{EA}{2}(a_1+2a_2X_1)^2 \,\mathrm{d}X_1 - P(a_1L+a_2L^2)\\ & = 9375a_1^2+\frac{100000}{3}a_1a_2+\frac{125000}{3}a_2^2-200(2a_1+4a_2) \end{split} \]

a_1 and a_2 are the variables that can be controlled to minimize the potential energy of the system. Therefore:

    \[ \frac{\partial PE}{\partial a_1}=0\Rightarrow -400+18750a_1+\frac{100000}{3}a_2=0 \]

and

    \[ \frac{\partial PE}{\partial a_2}=0\Rightarrow -800+\frac{100000}{3}a_1+\frac{250000}{3}a_2=0 \]

Solving the above two equations yields:

    \[ a_1=\frac{24}{1625}\qquad a_2=\frac{6}{1625} \]

Therefore, the best second degree polynomial according to the Rayleigh Ritz method is:

    \[ u_1=\frac{24}{1625}X_1+\frac{6}{1625}X_1^2 \]

A parabolic displacement would produce a linear stress:

    \[ \sigma_{11}=\frac{9600}{13}(2+X_1) \]

Polynomial of the Third Degree:
As a more refined approximation, we can assume that u_1 is a polynomial of the third degree:

    \[ u_1 = a_0+a_1 X_1+a_2X_1^2+a_3X_1^3 \]

To satisfy the essential boundary condition @X_1=0:u_1=0 the coefficient a_0 is equal to zero. Therefore:

    \[ u_1 = a_1 X_1+a_2X_1^2+a_3X_1^3 \]

The strain component \varepsilon_{11} can be computed as follows:

    \[ \varepsilon_{11}=\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=a_1+2a_2X_1+3a_3X_1^2 \]

Substituting into the equation for the potential energy of the system:

    \[\begin{split} PE&=\int_0^L\!\frac{EA}{2}(a_1+2a_2X_1+3a_3X_1^2)^2 \,\mathrm{d}X_1 - P(a_1L+a_2L^2+a_3L^3)\\ & = 9375a_1^2+\frac{100000}{3}a_1a_2+\frac{125000}{3}a_2^2+62500a_1a_3+180000a_2a_3+210000a_3^2\\ &-200(2a_1+4a_2+8a_3) \end{split} \]

a_1, a_2, and a_3 are the variables that can be controlled to minimize the potential energy of the system. Therefore:

    \[ \frac{\partial PE}{\partial a_1}=0\Rightarrow -400+18750a_1+\frac{100000}{3}a_2+62500a_3=0 \]

Also:

    \[ \frac{\partial PE}{\partial a_2}=0\Rightarrow -800+\frac{100000}{3}a_1+\frac{250000}{3}a_2+180000a_3=0 \]

And:

    \[ \frac{\partial PE}{\partial a_3}=0\Rightarrow -1600+62500a_1+180000a_2+420000a_3=0 \]

Solving the above three equations yields:

    \[ a_1=\frac{128}{7875}\qquad a_2=\frac{2}{1575} \qquad a_3=\frac{4}{4725} \]

Therefore, the best third degree polynomial according to the Rayleigh Ritz method is:

    \[ u_1=\frac{128}{7875}X_1+\frac{2}{1575}X_1^2+\frac{4}{4725}X_1^3 \]

A cubic displacement would produce a parabolic stress distribution:

    \[ \sigma_{11}=\frac{3200}{63}(32+5X_1(1+X_1)) \]

View Mathematica Code

Clear[u, u1, u2, u3, u4, stress, stress1, stress2, stress3, x]
(*Exact Solution*)
Ax = 25/100 (5/10 - 25/200*x);
Ee = 100000;
L = 2;
P = 200;
s = DSolve[{Ee*u''[x]*Ax + Ee*u'[x]*D[Ax, x] == 0, 
   u'[L] == 200/Ee/(Ax /. x -> L), u[0] == 0}, u, x]
u = u[x] /. s[[1]];
stress = Ee*D[u, x]
(*First Degree *)
u1 = a1*x;
PE = Integrate[1/2*Ee*D[u1, x]^2*Ax, {x, 0, L}] - P*u1 /. x -> L;
Eq1 = D[PE, a1];
s = Solve[Eq1 == 0, a1];
u1 = u1 /. s[[1]];
stress1 = Ee*D[u1, x];
(*Second Degree *)
u2 = a1*x + a2*x^2;
PE = Integrate[1/2*Ee*D[u2, x]^2*Ax, {x, 0, L}] - P*u2 /. x -> L;
Eq1 = D[PE, a1];
Eq2 = D[PE, a2];
s = Solve[{Eq1 == 0, Eq2 == 0}, {a1, a2}];
u2 = u2 /. s[[1]];
stress2 = Ee*D[u2, x];
(*Third Degree *)
u3 = a1*x + a2*x^2 + a3*x^3;
PE = Integrate[1/2*Ee*D[u3, x]^2*Ax, {x, 0, L}] - P*u3 /. x -> L;
Eq1 = D[PE, a1];
Eq2 = D[PE, a2];
Eq3 = D[PE, a3];
s = Solve[{Eq1 == 0, Eq2 == 0, Eq3 == 0}, {a1, a2, a3}];
u3 = u3 /. s[[1]];
stress3 = Ee*D[u3, x];
(*comparison*)
Plot[{u, u1, u2, u3}, {x, 0, L}, 
 PlotLegends -> {Style["Exact", Bold, 12], Style["u1", Bold, 12], 
   Style["u2", Bold, 12], Style["u3", Bold, 12]}, 
 AxesLabel -> {"X1 m", "u(m)"}, BaseStyle -> Directive[Bold, 12]]
Plot[{stress, stress1, stress2, stress3}, {x, 0, L}, 
 AxesLabel -> {"X1 m", "stress(Pa)"}, 
 BaseStyle -> Directive[Bold, 12], 
 PlotLegends -> {Style["Exact", Bold, 12], Style["u1", Bold, 12], 
   Style["u2", Bold, 12], Style["u3", Bold, 12]}]

View Python Code

from sympy import *
from numpy import * 
import sympy as sp 
import numpy as np
import matplotlib.pyplot as plt
sp.init_printing(use_latex = "mathjax")
x, a1, a2, a3, E, P = symbols("x a_1 a_2 a_3 E P")
Ax = 25/100*(5/10-25/200*x)
display("Exact")
u = Function("u")
u1_1 = u(x).subs(x,0)
u2_1 = u(x).diff(x).subs(x,L)
Ax1 = Ax.subs(x,L)
display("Area: ", Ax)
s = dsolve(E*u(x).diff(x,2)*Ax+E*u(x).diff(x)*Ax.diff(x), u(x), ics = {u1_1:0, u2_1:200/E/Ax1})
u = s.rhs.subs({E:100000, L:2, P:200})
stress0 = (E * u.diff(x)).subs({E:100000, L:2, P:200})
display("displacement and stress: ", u, stress0)
display("First Degree")
u1 = a1*x 
uL = u1.subs(x,L)
PE = integrate((1/2)*E*((u1.diff(x))**2)*Ax, (x,0,L)) - P*uL
PE = PE.subs({E:100000, L:2, P:200})
display("Potential Energy: ", PE)
Eq1 = PE.diff(a1)
display("Minimize:", Eq1)
s = solve(Eq1,a1)
display("Solve: ", s)
u1 = u1.subs(a1,s[0])
display("Best First degree Polynomial(Rayleigh Ritz method): ", u1)
stress1 = (E * u1.diff(x)).subs(E,100000)
display("stress: ", stress1)
display("Second Degree")
u2 = a1*x+a2*x**2
PE2 = integrate((1/2)*E*((u2.diff(x))**2)*Ax, (x,0,L)) - P*u2.subs(x,L)
PE2 = PE2.subs({E:100000, L:2, P:200})
display("Potential Energy: ", PE2)
Eq1_2 = PE2.diff(a1)
Eq2_2 = PE2.diff(a2)
s = solve((Eq1_2, Eq2_2),a1, a2)
display("Minimize:", Eq1_2, Eq2_2)
display("Solve: ", s)
u2 = u2.subs({a1:s[a1], a2:s[a2]})
display("Best Second degree Polynomial(Rayleigh Ritz method): ", u2)
stress2 = (E * u2.diff(x)).subs(E,100000)
display("stress: ", stress2)
display("Third Degree")
u3 = a1*x+a2*x**2+a3*x**3
PE3 = integrate((1/2)*E*((u3.diff(x))**2)*Ax, (x,0,L)) - P*u3.subs(x,L)
PE3 = PE3.subs({E:100000, L:2, P:200})
display("Potential Energy: ", PE3)
Eq1_3 = PE3.diff(a1)
Eq2_3 = PE3.diff(a2)
Eq3_3 = PE3.diff(a3)
s = solve((Eq1_3, Eq2_3, Eq3_3),a1, a2, a3)
display("Minimize:", Eq1_3, Eq2_3, Eq3_3)
display("Solve: ", s)
u3 = u3.subs({a1:s[a1], a2:s[a2], a3:s[a3]})
display("Best Third degree Polynomial(Rayleigh Ritz method): ", u3)
stress3 = (E * u3.diff(x)).subs(E,100000)
display("stress: ", stress3)
fig, ax = plt.subplots(1,2, figsize = (15,6))
plt.setp(ax[0], xlabel = "X1 m ", ylabel = "u(m)")
plt.setp(ax[1], xlabel = "X1 m", ylabel = "Stress(Pa)")
x1 = np.arange(0,2.5,0.5)
u_list = [u.subs({x:i}) for i in x1]
u1_list = [u1.subs({x:i}) for i in x1]
u2_list = [u2.subs({x:i}) for i in x1]
u3_list = [u3.subs({x:i}) for i in x1]
stress0_list = [stress0.subs({x:i}) for i in x1]
stress1_list = [stress1.subs({x:i}) for i in x1]
stress2_list = [stress2.subs({x:i}) for i in x1]
stress3_list = [stress3.subs({x:i}) for i in x1]
display("Comparison")
ax[0].plot(x1, u_list, 'blue', label = "exact")
ax[0].plot(x1, u1_list, 'orange', label = "u1")
ax[0].plot(x1, u2_list, 'green', label = "u2")
ax[0].plot(x1, u3_list, 'red', label = "u3")
ax[0].legend()
ax[1].plot(x1, stress0_list, 'blue', label = "exact")
ax[1].plot(x1, stress1_list, 'orange', label = "u1")
ax[1].plot(x1, stress2_list, 'green', label = "u2")
ax[1].plot(x1, stress3_list, 'red', label = "u3")
ax[1].legend()

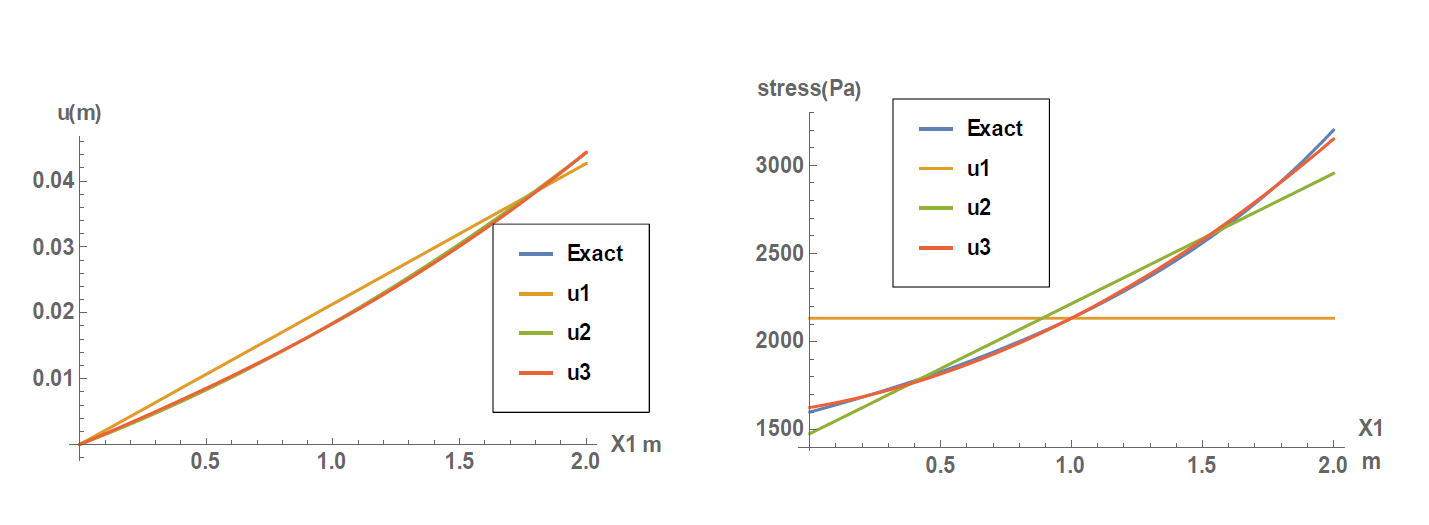
The exact solution obtained is a logarithmic function, while the approximations used for the Rayleigh Ritz method are polynomial functions. The Taylor series of a logarithmic function can be represented by a linear combination of polynomial functions, and so, the higher the degree of approximation, the closer the approximation to the exact solution. As seen in the plots below, good accuracy is obtained for a polynomial of the second degree for the displacement function; however, the stresses in that case have higher errors. A better approximation for the stresses is obtained using a polynomial of the third degree. In general, the error in the approximate solution (i.e., the error in u) is less than the error in its derivatives which in this case is the value of the strain component \varepsilon_{11}. This means as well that in order to achieve higher accuracy in the stress \sigma_{11}=E\frac{\mathrm{d}u_1}{\mathrm{d}X_1}, higher polynomials are needed.

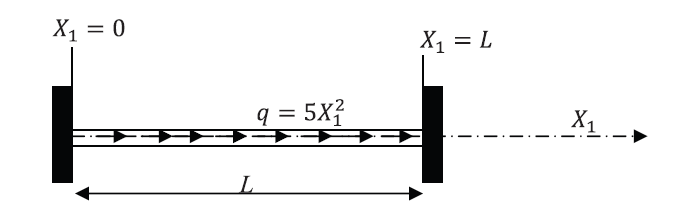
Example 3: A Bar Under Varying Body Forces With Fixed Ends

Let a bar with a length 2mbe aligned with the coordinate axis X_1, and let the cross sectional area A of the bar be equal to 250\times 250mm^2. Assume that the bar is fixed at both ends X_1= 0 and X_1=2m. Assume that the bar is subjected to a varying body force that is equal to p=5X_1^2 N/m in the direction of the coordinate axis X_1. Find the displacement of the bar by directly solving the differential equation of equilibrium and then using the Rayleigh Ritz method assuming polynomials of the degrees (0, 1, 2, 3, and 4). Assume that the bar material is linear elastic with Young’s modulus E=100,000 Pa and that the small strain tensor is the appropriate measure of strain. Ignore the effect of Poisson’s ratio. Compare the solution obtained using the Rayleigh Ritz method using three- and four-degree polynomials as approximations with the exact solution.

SOLUTION
Exact Solution:
Similar to the previous examples, the equilibrium equation is:

    \[ \frac{\mathrm{d}^2u_1}{\mathrm{d}X_1^2}=-\frac{p}{EA}=-\frac{5X_1^2}{0.25^2E} \]

Therefore, the solution for u_1 has the form:

    \[ u_1=-\frac{5X_1^4}{12(0.25)^2E}+C_1X_1+C_2 \]

The boundary conditions for this example are:

    \[\begin{split} @X_1=0&:u_1=0\Rightarrow C_2=0\\ @X_1=L&:u_1=0\Rightarrow C_1=\frac{5L^3}{12(0.25)^2E} \end{split} \]

Therefore the exact solutions for the displacement (in m) and the stress (in N/m^2) are:

    \[\begin{split} u_1&=\frac{8X_1-X_1^4}{15000}\\ \sigma_{11}&=\frac{20}{3}(8-4X_1^3) \end{split} \]

The Rayleigh Ritz Method:
The first step in the Rayleigh Ritz method finds the minimizer of the potential energy of the system which can be written as:

    \[ PE=\int\!\overline{U}\,dX - W=\int_0^L\!\frac{\sigma_{11}\varepsilon_{11}}{2}A \,\mathrm{d}X_1 - \int_0^L\!pu_1\,\mathrm{d}X_1 \]

Notice that the potential energy lost by the action of the distributed body forces is an integral since it acts on each point along the beam length. Further, we will use the constitutive equation to rewrite the potential energy function in terms of the function u_1:

    \[ PE=\int_0^L\!\frac{EA}{2}\left(\frac{\mathrm{d}u_1}{\mathrm{d}X_1}\right)^2 \,\mathrm{d}X_1 - \int_0^L\!5X_1^2u_1\,\mathrm{d}X_1 \]

To find an approximate solution, an assumption for the shape or the form of u_1 has to be introduced.
Polynomials of the Zero and First Degrees:
Assuming that that u_1 is a constant function (a polynomial of the zero degree) or a linear function (a polynomial of the first degree) and incorporating the boundary conditions:

    \[\begin{split} @X_1=0&:u_1=0\\ @X_1=L&:u_1=0 \end{split} \]

leads to the trivial solution u_1 = 0, which will automatically be rejected.

Polynomial of the Second Degree:
Let u_1 be a polynomial of the second degree:

    \[ u_1 = a_0+a_1 X_1+a_2X_1^2 \]

The essential boundary condition can be used to find values for the constants a_0 and a_2 as follows:

    \[\begin{split} @X_1=0&:u_1=0\Rightarrow a_0=0\\ @X_1=L&:u_1=0\Rightarrow a_2=-\frac{a_1}{L} \end{split} \]

Therefore, the displacement function has only one parameter a_1 that can be controlled:

    \[ u_1=a_1X_1\left(1-\frac{X_1}{L}\right) \]

The strain component \varepsilon_{11} can be computed as follows:

    \[ \varepsilon_{11}=\frac{\mathrm{d}u_1}{\mathrm{d}X_1}=a_1\left(1-2\frac{X_1}{L}\right) \]

Substituting into the equation for the potential energy of the system:

    \[\begin{split} PE&=\int_0^L\!\frac{EA}{2}\left(a_1\left(1-2\frac{X_1}{L}\right)\right)^2 \,\mathrm{d}X_1 -\int_0^L\!5X_1^2a_1X_1\left(1-\frac{X_1}{L}\right)\,\mathrm{d}X_1\\ & = \frac{6250}{3}a_1^2-4a_1 \end{split} \]

a_1 can be found by minimizing the potential energy of the system. Therefore:

    \[ \frac{\mathrm{d}PE}{\mathrm{d}a_1}=0\Rightarrow \frac{12500}{3}a_1-4=0\Rightarrow a_1=\frac{3}{3125} \]

Therefore, the best second degree polynomial according to the Rayleigh Ritz method is:

    \[ u_1=\frac{3X_1}{3125}\left(1-\frac{X_1}{2}\right) \]

A parabolic displacement would produce a linear stress:

    \[ \sigma_{11}=96(1-X_1) \]

Polynomials of Higher Degrees:
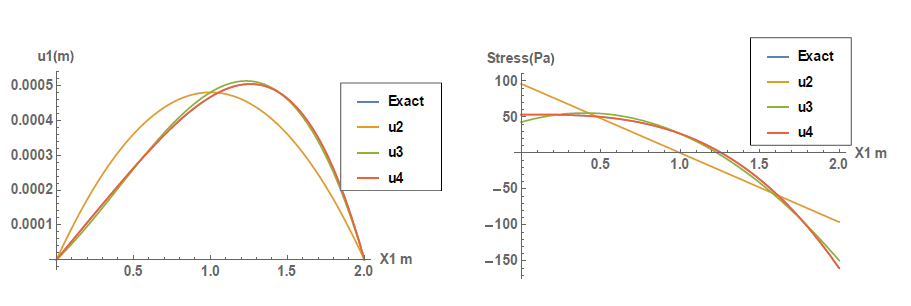
The results from the following Mathematica code show that the third-degree approximation is very close to the actual solution for both displacements and stresses. The polynomial of the fourth-degree approximation is in fact exact since the exact solution is a polynomial of the fourth degree. Study the Mathematica code carefully to understand how the second boundary conditions of displacement are incorporated. The graph comparing the results are shown below.

View Mathematica Code

Clear[u, x, a1, a2, a3, a4, a5, a0, Ee, A, L, p, u3, u4]
p = 5 x^2;
s = DSolve[{Ee*u''[x] == -p/A, u[L] == 0, u[0] == 0}, u, x];
u = u[x] /. s[[1]];
stress = Ee*D[u, x];
(*Second Degree*)
u2 = a2*x^2 + a1*x;
sol = Solve[(u2 /. x -> L) == 0, a2];
u2 = u2 /. sol[[1]];
PE = 1/2*Integrate[Ee*A*D[u2, x]^2, {x, 0, L}] - Integrate[p*u2, {x, 0, L}];
Eq1 = D[PE, a1];
sol1 = Solve[{Eq1 == 0}, {a1}];
u2 = FullSimplify[u2 /. sol1[[1]]];
stress2 = FullSimplify[Ee*D[u2, x]];
(*Third Degree*)
u3 = a3*x^3 + a2*x^2 + a1*x;
sol = Solve[(u3 /. x -> L) == 0, a3];
u3 = u3 /. sol[[1]];
PE = 1/2*Integrate[Ee*A*D[u3, x]^2, {x, 0, L}] - Integrate[p*u3, {x, 0, L}];
Eq1 = D[PE, a1];
Eq2 = D[PE, a2];
sol1 = Solve[{Eq1 == 0, Eq2 == 0}, {a2, a1}];
u3 = FullSimplify[u3 /. sol1[[1]]];
stress3 = FullSimplify[Ee*D[u3, x]];
(*Fourth Degree*)
u4 = a4*x^4 + a3*x^3 + a2*x^2 + a1*x;
sol = Solve[(u4 /. x -> L) == 0, a4];
u4 = u4 /. sol[[1]];
PE = 1/2*Integrate[Ee*A*D[u4, x]^2, {x, 0, L}] - Integrate[p*u4, {x, 0, L}];
Eq1 = D[PE, a1];
Eq2 = D[PE, a2];
Eq3 = D[PE, a3];
sol1 = Solve[{Eq1 == 0, Eq2 == 0, Eq3 == 0}, {a1, a2, a3}];
u4 = FullSimplify[u4 /. sol1[[1]]];
stress4 = FullSimplify[Ee*D[u4, x]];
A = (25/100)^2;
Ee = 100000;
L = 2;
(*comparison*)
Plot[{u, u2, u3, u4}, {x, 0, L}, PlotLegends -> {Style["Exact", Bold, 12], Style["u2", Bold, 12], Style["u3", Bold, 12], Style["u4", Bold, 12]}, AxesLabel -> {"X1 m", "u1(m)"}, BaseStyle -> Directive[Bold, 12]]
Plot[{stress, stress2, stress3, stress4}, {x, 0, L}, PlotLegends -> {Style["Exact", Bold, 12], Style["u2", Bold, 12], Style["u3", Bold, 12], Style["u4", Bold, 12]}, AxesLabel -> {"X1 m", "Stress(Pa)"}, BaseStyle -> Directive[Bold, 12]]

View Python Code

from sympy import *
from numpy import * 
import sympy as sp 
import numpy as np
import matplotlib.pyplot as plt
sp.init_printing(use_latex = "mathjax")
x, a1, a2, a3, a4, E, p, A, L= symbols("x a_1 a_2 a_3 a_4 E p A L")
p = 5*x**2
display("Exact")
u = Function("u")
u1_1 = u(x).subs(x,0)
u2_1 = u(x).subs(x,L)
s = dsolve(E*u(x).diff(x,2)+ p/A, u(x), ics = {u1_1:0, u2_1:0})
u = s.rhs.subs({E:100000, L:2, A:(25/100)**2})
stress0 = (E * u.diff(x)).subs({E:100000, L:2, A:(25/100)**2})
display("displacement and stress: ", u, stress0)
display("Second Degree")
u2 = a1*x+a2*x**2
sol = solve(u2.subs(x,L), a2)
u2 = u2.subs(a2,sol[0])
display("a2:", sol)
display(u2)
PE2 = (1/2)*(integrate(E*A*((u2.diff(x))**2), (x,0,L))) - integrate(p*u2, (x,0,L))
PE2 = PE2.subs({E:100000, L:2, A:(25/100)**2})
display("Potential Energy: ", PE2)
Eq1_2 = PE2.diff(a1)
sol1 = solve(Eq1_2,a1)
display("a1:", sol1)
u2 = u2.subs(a1,sol1[0]).subs(L,2)
display("Best Second degree Polynomial(Rayleigh Ritz method): ", u2)
stress2 = (E * u2.diff(x)).subs(E,100000)
display("stress: ", stress2)
display("Third Degree")
u3 = a1*x+a2*x**2+a3*x**3
sol = solve(u3.subs(x,L), a3)
display("a3: ", sol)
u3 = u3.subs(a3,sol[0])
PE3 = (1/2)*(integrate(E*A*((u3.diff(x))**2), (x,0,L))) - integrate(p*u3, (x,0,L))
PE3 = PE3.subs({E:100000, L:2, A:(25/100)**2})
display("Potential Energy: ", PE3)
Eq1_3 = PE3.diff(a1)
Eq2_3 = PE3.diff(a2)
sol1 = solve((Eq1_3, Eq2_3),a1, a2)
display("Minimize:", Eq1_3, Eq2_3)
display("Solve: ", sol1)
u3 = u3.subs({a1:sol1[a1], a2:sol1[a2], L:2})
display("Best Third degree Polynomial(Rayleigh Ritz method): ", u3)
stress3 = (E * u3.diff(x)).subs(E,100000)
display("stress: ", stress3)
display("Fourth Degree")
u4 = a1*x+a2*x**2+a3*x**3+a4*x**4
sol = solve(u4.subs(x,L), a4)
display("a4: ", sol)
u4 = u4.subs(a4,sol[0])
PE4 = (1/2)*(integrate(E*A*((u4.diff(x))**2), (x,0,L))) - integrate(p*u4, (x,0,L))
PE4 = PE4.subs({E:100000, L:2, A:(25/100)**2})
display("Potential Energy: ", PE4)
Eq1_4 = PE4.diff(a1)
Eq2_4 = PE4.diff(a2)
Eq3_4 = PE4.diff(a3)
sol1 = solve((Eq1_4, Eq2_4, Eq3_4),(a1, a2, a3))
display("Minimize:", Eq1_4, Eq2_4, Eq3_4)
display("Solve: ", sol1)
u4 = u4.subs({a1:sol1[a1], a2:sol1[a2], a3:sol1[a3]}).subs(L,2)
display("Best Fourth degree Polynomial(Rayleigh Ritz method): ", u3)
stress4 = (E * u4.diff(x)).subs(E,100000)
display("stress: ", stress4)
fig, ax = plt.subplots(1,2, figsize = (15,6))
plt.setp(ax[0], xlabel = "X1 m ", ylabel = "u(m)")
plt.setp(ax[1], xlabel = "X1 m", ylabel = "Stress(Pa)")
x1 = np.arange(0,2.1,0.1)
u_list = [u.subs({x:i}) for i in x1]
u2_list = [u2.subs({x:i}) for i in x1]
u3_list = [u3.subs({x:i}) for i in x1]
u4_list = [u4.subs({x:i}) for i in x1]
stress0_list = [stress0.subs({x:i}) for i in x1]
stress2_list = [stress2.subs({x:i}) for i in x1]
stress3_list = [stress3.subs({x:i}) for i in x1]
stress4_list = [stress4.subs({x:i}) for i in x1]
display("Comparison")
ax[0].plot(x1, u_list, 'blue', label = "exact")
ax[0].plot(x1, u2_list, 'orange', label = "u2")
ax[0].plot(x1, u3_list, 'green', label = "u3")
ax[0].plot(x1, u4_list, 'red', label = "u4")
ax[0].legend()
ax[1].plot(x1, stress0_list, 'blue', label = "exact")
ax[1].plot(x1, stress2_list, 'orange', label = "u2")
ax[1].plot(x1, stress3_list, 'green', label = "u3")
ax[1].plot(x1, stress4_list, 'red', label = "u4")
ax[1].legend()

Video:

Quiz 32 - Rayleigh Ritz Method

Solution Guide

Page Comments

  1. Burak Bayramli says:
    January 10, 2023 at 2:13 am

    Error on the Rayleigh Ritz Python Code, it says

    x, a1, a2, E, A, P, c = symbols(“x a_1 a_2 E A P c”)

    The symbol L is missing, it should be

    x, a1, a2, E, A, P, c, L = symbols(“x a_1 a_2 E A P c L”)

    Reply

Leave a Reply

Your email address will not be published.