Hyperelastic Materials: Frame-Indifferent Isotropic Hyperelastic Potential Energy Functions
As shown in the energy section, the increment in the internal energy inside a continuum per unit undeformed volume is given by the expression:
(1) ![]()
If the material is elastic, then, the strain energy developed during loading
![]()
is independent of the path of loading from state a to state b. To be independent of the path, Equation 1 has to be an exact differential. Therefore, an energy function ![]() has to exist such that the First Piola Kirchhoff stress
has to exist such that the First Piola Kirchhoff stress ![]() is derived from this strain energy function
is derived from this strain energy function ![]() , as follows:
, as follows:
![]()
i.e., the components of the first Piola Kirchhoff stress ![]() can be obtained by differentiating the strain energy density function
can be obtained by differentiating the strain energy density function ![]() with respect to the components of the deformation gradient:
with respect to the components of the deformation gradient:
![]()
The above expression indicates that the hyperelastic strain energy function per unit undeformed volume could be written as a function of the deformation gradient entries and the position ![]() :
:
![]()
However, we will assume in our treatment that the material is homogeneous, i.e., ![]() is independent of
is independent of ![]() . Therefore:
. Therefore:
![]()
Please see the book by Philippe Ciarlet for a rigorous treatment of the materials in this section.
Principle of Material Frame-Indifference
The principle of material frame-indifference implies that the strain energy stored inside the material should be independent of the coordinate system used to describe the deformed configuration. If a rotation ![]() is applied to the deformed configuration, then the strain energy function before applying the rotation should be equal to that after applying rotation, i.e.,
is applied to the deformed configuration, then the strain energy function before applying the rotation should be equal to that after applying rotation, i.e., ![]() such that
such that ![]() is a rotation:
is a rotation:
![]()
This automatically leads to the result that W is a function of the right-stretch tensor of the polar decomposition of the deformation gradient, as follows:
![]()
Since ![]() is arbitrary, it can be chosen such that
is arbitrary, it can be chosen such that ![]() . Then:
. Then:
![]()
The above relationship implies that the constitutive relationship describing the strain energy function is frame-indifferent if and only if it can be written as a real valued function of the components of ![]() . In other words, the strain energy density
. In other words, the strain energy density ![]() is a function defined on the set of positive definite symmetric matrices. Note that
is a function defined on the set of positive definite symmetric matrices. Note that ![]() is the positive definite symmetric matrix that is the unique square root of
is the positive definite symmetric matrix that is the unique square root of ![]() . I.e., the components of
. I.e., the components of ![]() can be written as a unique function of the components of U^2, then W can also be written as a function of the components of
can be written as a unique function of the components of U^2, then W can also be written as a function of the components of ![]() , i.e.,
, i.e., ![]() . Note that we are freely using the symbol W for the function even though the arguments could be the components of
. Note that we are freely using the symbol W for the function even though the arguments could be the components of ![]() or
or ![]() .
.
Symmetry of the Cauchy Stress Tensor
The symmetry of the Cauchy stress tensor imposes some restrictions on the possible forms of the function ![]() . The Cauchy stress tensor has the form:
. The Cauchy stress tensor has the form:
![]()
If the strain energy density function is given as a function of ![]() , then
, then ![]() has to satisfy the relationship:
has to satisfy the relationship:
![]()
In the following, it will be shown that a hyperelastic material whose strain energy function satisfies the principle of material frame-indifference implies that the Cauchy stress matrix is symmetric. Assuming that ![]() , we will show that the this implies that
, we will show that the this implies that ![]() is symmetric. First, we will find the component form of the fourth order tensor
is symmetric. First, we will find the component form of the fourth order tensor ![]() as follows:
as follows:
![]()
Therefore:
![]()
Then, the components of the term ![]() can be written as follows by considering that
can be written as follows by considering that ![]() is a function of the components of
is a function of the components of ![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{split} \left(\frac{\partial W}{\partial F}F^T\right)_{lk}&=\frac{\partial W}{\partial C_{ij}}\frac{\partial C_{ij}}{\partial F_{lm}}F_{km}=\frac{\partial W}{\partial C_{ij}}\left(F_{ki}\delta_{kl}\delta_{jm}+F_{kj}\delta_{kl}\delta_{im}\right)F_{km}\\ &=\frac{\partial W}{\partial C_{ij}}\left(F_{ki}\delta_{kl}\delta_{jm}\right)F_{km}+\frac{\partial W}{\partial C_{ij}}\left(F_{kj}\delta_{kl}\delta_{im}\right)F_{km}\\ &=\frac{\partial W}{\partial C_{im}}F_{li}F_{km}+\frac{\partial W}{\partial C_{mj}}F_{lj}F_{km} \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-ec8c3b17ee81883e45bc15619774930f_l3.png)
Since ![]() in the first term is arbitrary, it can be replaced with
in the first term is arbitrary, it can be replaced with ![]() . Therefore:
. Therefore:
![]()
Therefore:
![]()
The right hand side of the above equation is a symmetric matrix. Therefore, ![]() is symmetric, i.e., the Cauchy stress matrix is symmetric. Intuitively, a material model whose strain energy density is only a function of the stretch part of
is symmetric, i.e., the Cauchy stress matrix is symmetric. Intuitively, a material model whose strain energy density is only a function of the stretch part of ![]() is not affected by rotations following the stretch
is not affected by rotations following the stretch ![]() , i.e., rigid rotations of the material points are not accompanied by any energy and are not accompanied by any internal resistance, which is intuitively related to the balance of angular momentum.
, i.e., rigid rotations of the material points are not accompanied by any energy and are not accompanied by any internal resistance, which is intuitively related to the balance of angular momentum.
Notice that the form of ![]() can be chosen such that
can be chosen such that ![]() is symmetric. This can be achieved by simply considering
is symmetric. This can be achieved by simply considering ![]() to be a real valued function whose arguments are the components of symmetric matrices. In that case we have:
to be a real valued function whose arguments are the components of symmetric matrices. In that case we have:
![]()
Isotropy
If a material is isotropic, then the strain energy function is independent of the orientation of the material vectors. In other words, if a rotation ![]() is applied to the undeformed configuration and then the material is deformed such that
is applied to the undeformed configuration and then the material is deformed such that ![]() describes the new deformation, then the strain energy function of an isotropic material should be equal irrespective of the value of the applied rotation
describes the new deformation, then the strain energy function of an isotropic material should be equal irrespective of the value of the applied rotation ![]() . I.e., for isotropic materials:
. I.e., for isotropic materials: ![]() with
with ![]() being a rotation:
being a rotation:
![]()
Using the singular value decomposition ![]() of the deformation gradient and the results of the principle of material frame-indifference of
of the deformation gradient and the results of the principle of material frame-indifference of ![]() :
:
![]()
Thus, the strain energy function of an isotropic hyperelastic material can be described as a function of the principal stretches (the singular values of ![]() ). Moreover,
). Moreover, ![]() should be isotropic in the variables
should be isotropic in the variables ![]() , and
, and ![]() (Why?).
(Why?).
Possible Arguments of the Isotropic Hyperelastic Strain Energy Function
Let ![]() be the deformation gradient of a given deformation,
be the deformation gradient of a given deformation, ![]() , and
, and ![]() be the associated principal stretches,
be the associated principal stretches, ![]() is the right polar decomposition and
is the right polar decomposition and ![]() . Then the strain energy density function can equivalently be written as a function of any of the following arguments:
. Then the strain energy density function can equivalently be written as a function of any of the following arguments:
![]()
PROOF:
First, we prove the following statement: Let ![]() be three sets and let
be three sets and let ![]() and
and ![]() be well defined functions. Then, if
be well defined functions. Then, if ![]() with
with ![]() imply
imply ![]() , then
, then ![]() can be viewed as a well defined function of only
can be viewed as a well defined function of only ![]() . The proof is straightforward, let
. The proof is straightforward, let ![]() be defined as
be defined as ![]() . We will show that
. We will show that ![]() is well defined. Let
is well defined. Let ![]() and
and ![]() with
with ![]() . If
. If ![]() is unique to
is unique to ![]() then
then ![]() is well defined. Otherwise,
is well defined. Otherwise, ![]() such that
such that ![]() . However, the conditions of the statement imply that
. However, the conditions of the statement imply that ![]() , therefore,
, therefore, ![]() is well defined. Therefore,
is well defined. Therefore, ![]() admits the form
admits the form ![]() . For simplicity, we write
. For simplicity, we write ![]() .
.
Clarification: A counter example to this statement is considering the real valued functions ![]() such that
such that ![]() and
and ![]() such that
such that ![]() . It is not possible to write
. It is not possible to write ![]() as a function of
as a function of ![]() , since if we choose the positive square root, then
, since if we choose the positive square root, then ![]() but
but ![]() which contradicts that
which contradicts that ![]() . On the other hand, if we define
. On the other hand, if we define ![]() and
and ![]() , then these functions satisfy the conditions of the statement, i.e., if
, then these functions satisfy the conditions of the statement, i.e., if ![]() then
then ![]() . f can be written as a well defined function of
. f can be written as a well defined function of ![]() with the form:
with the form: ![]() .
.
We now apply this statement to the functions ![]() and
and ![]() defined as:
defined as:
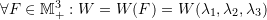 where
where  is the set of matrices with positive determinant and
is the set of matrices with positive determinant and 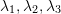 are the singular values of
are the singular values of 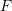 .
.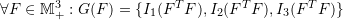 .
.
The section on Matrix Invariants show that if two matrices share the same invariants, then they share the same eigenvalues. I.e., if ![]() are such that
are such that ![]() then the eigenvalues of
then the eigenvalues of ![]() and
and ![]() are the same. Since
are the same. Since ![]() and
and ![]() have positive determinants, therefore,
have positive determinants, therefore, ![]() and
and ![]() are positive definite with positive eigenvalues (See The Polar Decomposition of the Deformation Gradient). Therefore, the singular values which are the positive square roots of the eigenvalues of
are positive definite with positive eigenvalues (See The Polar Decomposition of the Deformation Gradient). Therefore, the singular values which are the positive square roots of the eigenvalues of ![]() and
and ![]() are the same. Therefore,
are the same. Therefore, ![]() . Therefore
. Therefore ![]() can be written as a function of only the invariants
can be written as a function of only the invariants ![]() . The same argument can be applied to the remaining expressions.
. The same argument can be applied to the remaining expressions.
Some authors prefer to write ![]() as an additive decomposition of a “volumetric” component and an “isochoric” or “deviatoric” component. This is done by considering the matrix
as an additive decomposition of a “volumetric” component and an “isochoric” or “deviatoric” component. This is done by considering the matrix ![]() . Note that in this case,
. Note that in this case, ![]() . W can be written as a function of
. W can be written as a function of ![]() and
and ![]() . In particular:
. In particular:
![]()
where ![]() and
and ![]() are two scalar functions. It is important to note that the additive nature of this energy function is a special form and is inherited from the possibility of having this additive decomposition of the energy in linear elasticity.
are two scalar functions. It is important to note that the additive nature of this energy function is a special form and is inherited from the possibility of having this additive decomposition of the energy in linear elasticity.
Physical Restrictions On 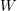
There are a few restrictions on the possible forms of ![]() derived from physical reasoning on the possible deformations of elastic materials. The first restriction is that, when the reference configuration is the undeformed configuration, i.e., when the stretching part of the deformation gradient is the identity matrix, then
derived from physical reasoning on the possible deformations of elastic materials. The first restriction is that, when the reference configuration is the undeformed configuration, i.e., when the stretching part of the deformation gradient is the identity matrix, then ![]() has to be minimum. In other words:
has to be minimum. In other words:
![]()
The second restriction is that as the material is compressed such that the volume approaches zero or the material is stretched such that the volume approaches infinity, then the strain energy is expected to approach infinity:
![]()
![]()
Additionally, if the stretch in any direction approaches infinity, then the strain energy is expected to approach infinity as well:
![]()
Traditionally, the elastic potential-energy density function ![]() of an isotropic hyperelastic material is written as a function of the quantities:
of an isotropic hyperelastic material is written as a function of the quantities:
![]()
with the following physical interpretation of each quantity:![]() is a principal stretch,
is a principal stretch, ![]() , and
, and ![]() is the deformed area of a unit area perpendicular to the direction of
is the deformed area of a unit area perpendicular to the direction of ![]() .
.
