Strain Measures: Examples and Problems
Example 1:
Calculate the infinitesimal and Green strain matrices for the following position function:
![Rendered by QuickLaTeX.com \[ x=\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)=\left(\begin{matrix}1.2 & 0.2 & 0.2\\0.2& 1.3 & 0.1\\0.9&0.5&1\end{matrix}\right)\left(\begin{array}{c}X_1\\X_2\\X_3\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-9c49f811f293d484b073424ad2b15525_l3.png)
Also, find the displacement function, the uniaxial small and Green strains along the direction of the vector 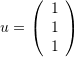 .
.
Solution:
The displacement function is:
![Rendered by QuickLaTeX.com \[ u=x-X=\left(\begin{matrix}0.2 & 0.2 & 0.2\\0.2& 0.3 & 0.1\\0.9&0.5&0\end{matrix}\right)\left(\begin{array}{c}X_1\\X_2\\X_3\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8cd3aeef4dc35cff9ff61885591f71d5_l3.png)
The small strain tensor is:
![Rendered by QuickLaTeX.com \[ \varepsilon_{small}=\frac{1}{2}\left(\nabla u + \nabla u^T\right)=\left(\begin{matrix}0.2 & 0.2 & 0.55\\0.2& 0.3 & 0.3\\0.55&0.3&0\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c196bfaa7d356de74c89c2d92de82a31_l3.png)
The Green strain tensor is:
![Rendered by QuickLaTeX.com \[ \varepsilon_{Green}=\frac{1}{2}\left(\nabla u + \nabla u^T+\nabla u^T\nabla u\right)=\left(\begin{matrix}0.645 & 0.475 & 0.58\\0.475& 0.49 & 0.335\\0.58&0.335&0.025\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-35d8931b2b19b6d967f4ffdff464535c_l3.png)
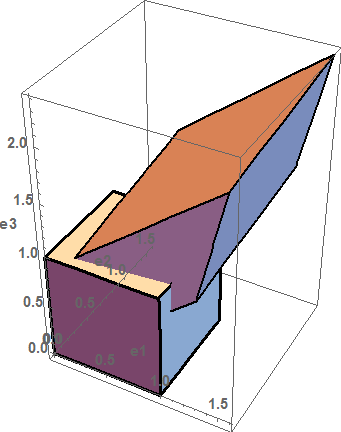
The deformation is very large as shown by applying this deformation to a unit cube (see figure below), so the strain measures are different.
The uniaxial small and Green strain along the vector ![]() can be obtained as follows:
can be obtained as follows:
![]()
View Mathematica Code
X={X1,X2,X3};
x=F.X;
u=x-X;
Gradu=Table[D[u[[i]],X[[j]]],{i,1,3},{j,1,3}]
einfinitesimal=1/2*(Gradu+Transpose[Gradu]);
%//MatrixForm
egreen=1/2*(Gradu+Transpose[Gradu]+Transpose[Gradu].Gradu);
%//MatrixForm
u={1,1,1};
n=u/Norm[u];
n.einfinitesimal.n
n.egreen.n
Box1=Cuboid[{0,0,0},{1,1,1}];
Box2=GeometricTransformation[Box1,F];
Graphics3D[{EdgeForm[Thickness[0.01]],Box1,EdgeForm[Thickness[0.005]],Box2},Axes->True,AxesOrigin->{0,0,0},BaseStyle->Directive[Bold,15],AxesLabel->{e1,e2,e3}]
View Python Code
from sympy import *
import sympy as sp
sp.init_printing(use_latex="mathjax")
F = Matrix([[1.2,0.2,0.2],[0.2,1.3,0.1],[0.9,0.5,1]])
X1,X2,X3 = sp.symbols("X1 X2 X3")
x1,x2,x3 = sp.symbols("x1 x2 x3")
X = Matrix([X1,X2,X3])
x = Matrix([x1,x2,x3])
display("X =",X)
display("x =",x)
display("x = F.X =",F*x)
x = F*X
u = x-X
display("u = x-X =",u)
gradu = Matrix([[diff(i,j) for j in X] for i in u])
display("\u2207u =",gradu)
small_strain = (gradu+gradu.T)/2
display("\u03B5_small =",small_strain)
green_strain = (gradu+gradu.T+gradu.T*gradu)/2
display("\u03B5_Green =",green_strain)
v = Matrix([1,1,1])
n = v/v.norm()
display("small strain along u", n.dot(small_strain*n))
display("Green strain along u", n.dot(green_strain*n))
Example 2:
A cube of unit dimensions undergoes a rigid body rotation in ![]() of
of ![]() , then
, then ![]() , and then
, and then ![]() around the basis vectors
around the basis vectors ![]() and
and ![]() respectively. Use Mathematica to visualize the box. Compare the two strain measures
respectively. Use Mathematica to visualize the box. Compare the two strain measures ![]() and
and ![]() .
.
SOLUTION:
The deformation gradient is given by:
![Rendered by QuickLaTeX.com \[ F=Q_{e_1}Q_{e_2}Q_{e_3}=\left(\begin{matrix}0.883&-0.3214 & 0.3420\\0.4569&0.7553 & -0.4698\\-0.1073 & 0.5712 & 0.8138\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-deddf4834ec70d599c0b469f24d13789_l3.png)
Note that ![]() is on the right since it is applied first.
is on the right since it is applied first.
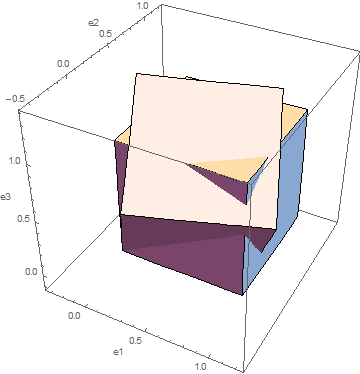
The Green strain is identically zero while the small strain tensor predicts the following strains:
![Rendered by QuickLaTeX.com \[ \varepsilon_{small}=\left(\begin{matrix}-0.117&0.068& 0.117\\0.068&-0.245 & 0.050\\0.117 & 0.051& -0.186\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-55a4600d2885dd5d99df78cba94a60c6_l3.png)
View Mathematica Code
Qy=RotationMatrix[thy,{0,1,0}];
Qz=RotationMatrix[thz,{0,0,1}];
thx=30Degree
thy=20Degree
thz=20Degree
F=Qx.Qy.Qz;
X={X1,X2,X3};
x=F.X;
u=x-X;
Gradu=Table[D[u[[i]],X[[j]]],{i,1,3},{j,1,3}];
einfinitesimal=1/2*(Gradu+Transpose[Gradu]);
einfinitesimal=FullSimplify[einfinitesimal];
%//MatrixForm
egreen=1/2*(Gradu+Transpose[Gradu]+Transpose[Gradu].Gradu);
egreen=FullSimplify[egreen];
%//MatrixForm
Box1=Cuboid[{0,0,0},{1,1,1}];
Box2=GeometricTransformation[Box1,F];
Graphics3D[{Box1,Box2},Axes->True,AxesOrigin->{0,0,},AxesLabel->{e1,e2,e3}]
View Python Code
from sympy import *
import sympy as sp
theta = sp.symbols("\u03B8")
X1,X2,X3=sp.symbols("X1 X2 X3")
x1,x2,x3=sp.symbols("x1 x2 x3")
Qx = Matrix([[1, 0, 0],
[0, sp.cos(theta),-sp.sin(theta)],
[0, sp.sin(theta),sp.cos(theta)]])
# y rotation matrix
Qy = Matrix([[sp.cos(theta), 0, sp.sin(theta)],
[0, 1, 0],
[-sp.sin(theta), 0, sp.cos(theta)]])
# z rotation matrix
Qz = Matrix([[sp.cos(theta), -sp.sin(theta), 0],
[sp.sin(theta), sp.cos(theta), 0],
[0, 0, 1]])
Qx = Qx.subs({theta:30*sp.pi/180})
Qy = Qy.subs({theta:20*sp.pi/180})
Qz = Qz.subs({theta:20*sp.pi/180})
F = Qx*Qy*Qz
display("F =",F)
F = simplify(F).evalf()
display("F =",F)
X=Matrix([X1,X2,X3])
x=Matrix([x1,x2,x3])
display("X =",X)
display("x =",x)
display("x =F.X =",F*x)
x = F*X
u = x-X
display("u = x-X =",u)
gradu = Matrix([[diff(i,j) for j in X] for i in u])
display("\u2207u =",gradu)
small_strain = (gradu+gradu.T)/2
display("\u03B5_small =",small_strain)
green_strain = (gradu+gradu.T+gradu.T*gradu)/2
display("\u03B5_Green =",green_strain)
Example 3:
A cube of unit length undergoes a simple shearing motion of an angle ![]() in the direction of
in the direction of ![]() and perpendicular to
and perpendicular to ![]() . Find the infinitesimal and Green strain measures that describe this motion. Comment on the difference between the two strain measures.
. Find the infinitesimal and Green strain measures that describe this motion. Comment on the difference between the two strain measures.
SOLUTION:
The position function is given by:
![Rendered by QuickLaTeX.com \[ x=\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)=\left(\begin{array}{c}X_1+\tan\theta X_2\\X_2\\X_3\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f973bae812a27521f18ac64bc9d3c9e1_l3.png)
The deformation gradient is given by:
![Rendered by QuickLaTeX.com \[ F=\left(\begin{matrix}1&\tan\theta & 0\\0&1&0\\0&0&1\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-8fc84bbec817834c66a9bf93e3633cbe_l3.png)
The small strain and Green strain tensors are given by:
![Rendered by QuickLaTeX.com \[ \varepsilon_{small}=\left(\begin{matrix}0&\frac{\tan\theta}{2} & 0\\\frac{\tan\theta}{2}&0&0\\0&0&0\end{matrix}\right)\qquad \varepsilon_{Green}=\left(\begin{matrix}0&\frac{\tan\theta}{2} & 0\\\frac{\tan\theta}{2}&\frac{\tan^2\theta}{2}&0\\0&0&0\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-65f79e8c2581e34abef28e2fa5c73df0_l3.png)
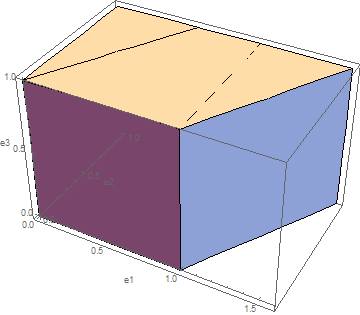
Both measures predict the same shear strains. For small deformations, both measures predict zero normal strains. As the ![]() increases, the vertical lines start developing large axial strains which the
increases, the vertical lines start developing large axial strains which the ![]() can predict while
can predict while ![]() cannot. The undeformed and deformed shapes of the cube are shown below for
cannot. The undeformed and deformed shapes of the cube are shown below for ![]() .
.
View Mathematica Code
X={X1,X2,X3};
x=F.X;
u=x-X;
Gradu=Table[D[u[[i]],X[[j]]],{i,1,3},{j,1,3}]
einfinitesimal=1/2*(Gradu+Transpose[Gradu]);
einfinitesimal=FullSimplify[einfinitesimal];
%//MatrixForm
egreen= 1/2*(Gradu+Transpose[Gradu]+Transpose[Gradu].Gradu);
egreen=FullSimplify[egreen];
%//MatrixForm
Box1=Cuboid[{0,0,0},{1,1,1}];
Box2=GeometricTransformation[Box1,F];
theta=30Degree;
Graphics3D[{Box1,Box2},Axes->True,AxesOrigin->{0,0,0},AxesLabel->{e1,e2,e3}]
View Python Code
from sympy import *
import sympy as sp
sp.init_printing(use_latex="mathjax")
X1, X2, X3 = sp.symbols("X_1 X_2 X_3")
theta = sp.symbols("\u03B8")
X = Matrix([X1, X2, X3])
F = Matrix([[1,tan(theta),0],[0,1,0],[0,0,1]])
display("deformation gradient:")
display("F =",F)
x = F*X
display("position function:")
display("x =",x)
u = x-X
display("u = x-X =",u)
gradu = Matrix([[diff(i,j) for j in X] for i in u])
display("\u2207u =",gradu)
small_strain = (gradu+gradu.T)/2
display("\u03B5_small =",small_strain)
green_strain = (gradu+gradu.T+gradu.T*gradu)/2
display("\u03B5_Green =",green_strain)
Example 4:
The following small strain matrix represents a two dimensional state of strain
![]()
Find the principal strains and their directions. If a coordinate system is aligned with the principal directions, find the components of the strain matrix in this new coordinate system.
SOLUTION:
The principal strains ![]() and
and ![]() and their directions
and their directions ![]() , and
, and ![]() be obtained using Mathematica by finding the eigenvalues and eigenvectors of
be obtained using Mathematica by finding the eigenvalues and eigenvectors of ![]() . The following are the eiganvalues:
. The following are the eiganvalues:
![]()
The following are the normalized eigenvectors.
![]()
The transformation matrix between the original coordinate system and the new coordinate system is:
![]()
The strain matrix in the new coordinate system has the form:
![]()
View Mathematica Code
s=Eigensystem[eps]
Q={-s[[2,1]],-s[[2,2]]}
epsdash=Chop[Q.eps.Transpose[Q]]
View Python Code
from sympy import *
import sympy as sp
sp.init_printing(use_latex="mathjax")
small_strain = Matrix([[0.01, 0.012],[0.012, 0]])
display("\u03B5_small =",small_strain)
# eigenvalues
eigensystem = small_strain.eigenvects()
display("eigensystem", eigensystem)
eigenvalues = [i[0] for i in eigensystem]
eigenvectors = [i[2][0].T for i in eigensystem]
neigenvectors = [i/i.norm() for i in eigenvectors]
display("eigenvalues (principal strains) =",eigenvalues)
display("eigenvectors (principal directions) =",eigenvectors)
display("Normalized eigenvectors (principal directions) =",neigenvectors)
#The function Matrix ensures the list is a sympy matrix
Q = Matrix(neigenvectors)
display("Diagonalized matrix = Q.M.Q^T",Q*small_strain*Q.T)
display("Diagonalized matrix = Q.M.Q^T",N(Q*small_strain*Q.T,chop=True))
Example 5:
A state of uniform small strain is described by the following small strain matrix:
![Rendered by QuickLaTeX.com \[ \varepsilon_{small}=\left(\begin{matrix}-0.01 & 0.002 & -0.023 \\ 0.002 & 0.05 & 0\\ -0.023 & 0 & 0.02\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fff54f61561005ccd41fda2a41992131_l3.png)
Determine the following:
- The longitudinal strain along the direction of the vector
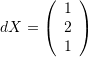 .
. - The change in the cosines of the angles between the vectors
 and
and 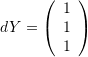 and comment on whether the angle between the vectors decreased or increased after deformation.
and comment on whether the angle between the vectors decreased or increased after deformation. - The shear strains of planes parallel to the vector
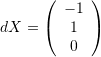 and perpendicular to the vector
and perpendicular to the vector 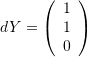 .
.
SOLUTION:
The strains along 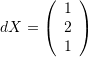 can be calculated as follows:
can be calculated as follows:
![]()
The change in the cosines of the angles between the vectors  and
and 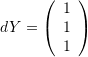 can be calculated as follows:
can be calculated as follows:
![]()
The angle ![]() between the vectors
between the vectors ![]() and
and ![]() before deformation can be calculated using the dot product:
before deformation can be calculated using the dot product:
![]()
Therefore, the angle ![]() after deformation between the vectors is larger because:
after deformation between the vectors is larger because:
![]()
Since the vectors 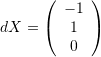 and
and 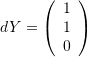 are perpendicular, the shear strains of planes parallel to the vector
are perpendicular, the shear strains of planes parallel to the vector ![]() and perpendicular to the vector
and perpendicular to the vector ![]() can be obtained as follows:
can be obtained as follows:
![]()
View Mathematica Code
dX={1,2,1};
Norm[dX]
Eps.dX
dX.Eps.dX/Norm[dX]^2
dX={1,0,1};
dY={1,1,1};
anglechange=dX.Eps.dY/Norm[dX]/Norm[dY]
THETA=N[ArcCos[dX.dY/Norm[dX]/Norm[dY]]]
THETA/Degree
theta=ArcCos[2*anglechange+Cos[THETA]]
theta/Degree
dX={-1,1,0};
dY={1,1,0};
ShearSTrain=dX.Eps.dY/Norm[dX]/Norm[dY]
View Python Code
import sympy as sp
from sympy import *
sp.init_printing(use_latex="mathjax")
small_strain = Matrix([[-0.01, 0.002, -0.023],[0.002, 0.05, 0],[-0.023, 0, 0.02]])
display("\u03B5_small =",small_strain)
# part 1
display("part 1")
dX = Matrix([1,2,1])
display("dX =",dX)
display("norm of dX =",dX.norm())
ndX = dX/dX.norm()
display("small strain along dX =",ndX.dot(small_strain*ndX))
# part 2
display("part 2")
dX = Matrix([1,0,1])
dY = Matrix([1,1,1])
display("dX =",dX)
display("dY =",dY)
ndX = dX/dX.norm()
ndY = dY/dY.norm()
small_strain_along = ndX.dot(small_strain*ndY)
display("1/2 change of cos of angle between dX and dY =",small_strain_along.evalf())
phi = acos(ndX.dot(ndY)).evalf()
display("\u03A6 =",phi,"degrees", deg(phi).evalf())
theta = acos(small_strain_along*2 + cos(phi))
display("\u03B8 =",theta,"degrees", deg(theta).evalf())
# part 3
display("part 3")
dX = Matrix([-1,1,0])
dY = Matrix([1,1,0])
display("dX =",dX)
display("dY =",dY)
ndX = dX/dX.norm()
ndY = dY/dY.norm()
display("shear strain =",ndX.dot(small_strain*ndY).evalf())
Example 6:
The longitudinal engineering strains on the surface of a test specimen were measured using a strain gauge rosette to be 0.005, 0.002 and –0.001 along the three directions: ![]() ,
, ![]() , and
, and ![]() respectively, where
respectively, where ![]() . If the material is assumed to be in a small strain state, find the principal strains and their directions on the surface of the test specimen.
. If the material is assumed to be in a small strain state, find the principal strains and their directions on the surface of the test specimen.
SOLUTION:
The state of strain on the surface of the material can be represented by the symmetric small strain matrix:
![]()
Since the longitudinal strain is known along three directions, three equations can be written to find the three unknown components of the strain matrix as follows:
![]()
The norm of each of a, b, and c is 1. Therefore, the three equations are:
![Rendered by QuickLaTeX.com \[ \begin{split} \frac{1}{4}\left(3\varepsilon_{11}+2\sqrt{3}\varepsilon_{12}+\varepsilon_{22}\right) & = 0.005 \\ \varepsilon_{22}& = 0.002\\ \frac{1}{4}\left(3\varepsilon_{11}-2\sqrt{3}\varepsilon_{12}+\varepsilon_{22}\right) & = -0.001 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-2787e62c42c1354d306768ef7a67d92a_l3.png)
Solving the above three equations yields:
![]()
The principal strains and their directions are the eigenvalues and eigenvectors of the small strain matrix. The principal strains are:
![]()
The principal directions are:
![]()
View Mathematica Code
a={Cos[30Degree],Sin[30Degree]};
b={0,1};
c={-Cos[30Degree],Sin[30Degree]};
FullSimplify[a.eps.a/Norm[a]^2]
FullSimplify[b.eps.b/Norm[b]^2]
FullSimplify[c.eps.c/Norm[c]^2]
a=Solve[{a.eps.a/Norm[a]^2==0.005,b.eps.b/Norm[b]^2==0.002,c.eps.c/Norm[c]^2==-0.001,eps[[1,2]]==eps[[2,1]]},Flatten[eps]]
eps=eps/.a[[1]];
Eigensystem[eps]//MatrixForm
View Python Code
from sympy import *
import sympy as sp
sp.init_printing(use_latex="mathjax")
E11, E12, E22 = sp.symbols("\u03B5_{11} \u03B5_{12} \u03B5_{22}")
E_s = sp.symbols("\u03B5_{small}=")
E_small = Matrix([[E11, E12],[E12, E22]])
display(E_s,E_small)
theta = sp.symbols("\u03B8")
a = Matrix([sp.cos(theta), sp.sin(theta)])
b = Matrix([0,1])
c = Matrix([-sp.cos(theta), sp.sin(theta)])
a, c = a.subs({theta:30*sp.pi/180}), c.subs({theta:30*sp.pi/180})
display("a =",a)
display("b =",b)
display("c =",c)
strain = Matrix([Rational('5/1000'), Rational('2/1000'),Rational('-1/1000')])
eq1 = simplify(a.dot(E_small*a)) - strain[0]
eq2 = simplify(b.dot(E_small*b)) - strain[1]
eq3 = simplify(c.dot(E_small*c)) - strain[2]
display("Systems of equations:")
display(eq1)
display(eq2)
display(eq3)
sol = solve([eq1, eq2, eq3],[E11, E12, E22])
E_small = E_small.subs({E11:sol[E11],E12:sol[E12],E22:sol[E22]})
display(E_s,E_small)
E_small = N(E_small)
display(E_s,E_small)
eigensystem = E_small.eigenvects()
display("eigensystem", eigensystem)
eigenvalues=[i[0] for i in eigensystem]
eigenvectors=[i[2][0].T for i in eigensystem]
neigenvectors=[i/i.norm() for i in eigenvectors]
display("eigenvalues (principal strains) =",eigenvalues)
display("eigenvectors (principal directions) =",eigenvectors)
display("Normalized eigenvectors (principal directions) =",neigenvectors)
Example 7:
In the above examples, the deformation was described by a uniform strain matrix (i.e., a strain matrix that is not function in position). In this example, a nonuniform strain, i.e., the strain matrix is function of position is explored. Assume that the two dimensional displacement function of a 2units by 2units plate has the following form:
![]()
- Find the deformed configuration function
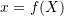 .
. - Find
 and
and 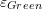 .
. - Draw the vector plot of the displacement function on the plate.
- Draw the contour plots of
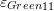 ,
, 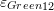 ,
,  , and
, and  on the plate.
on the plate.
SOLUTION:
The position function of the deformed configuration is given by:
![]()
The deformation gradient is given by:
![]()
The displacement gradient is given by:
![]()
Therefore, the small strain matrix is given by:
![]()
The Green strain matrix is given by:
![]()
The required plots are shown below.
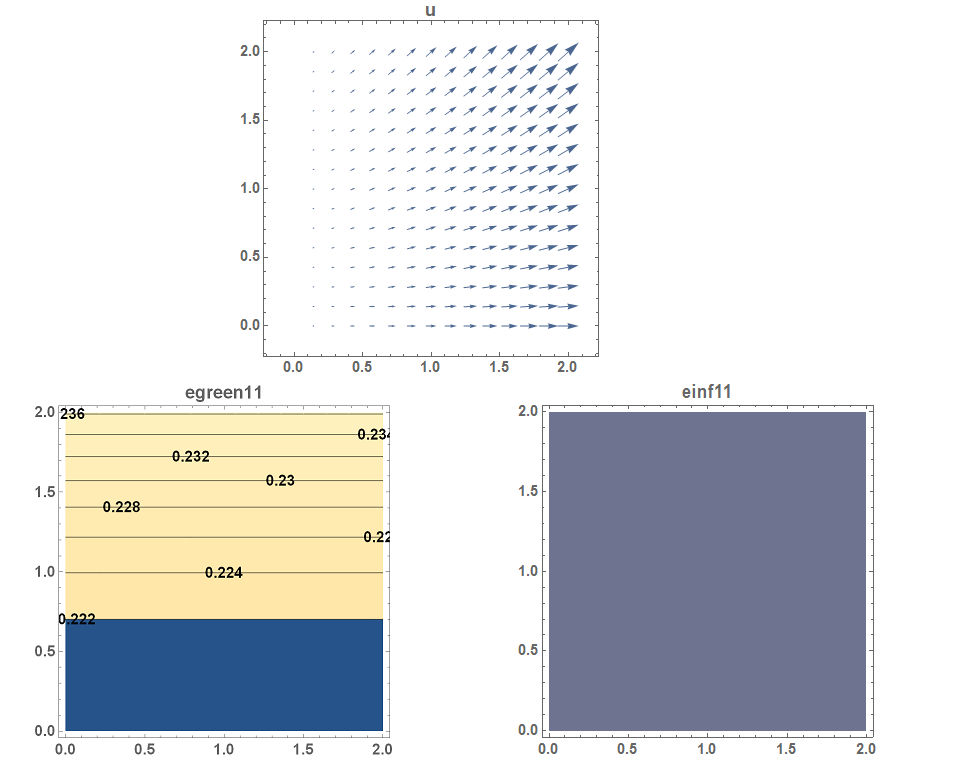
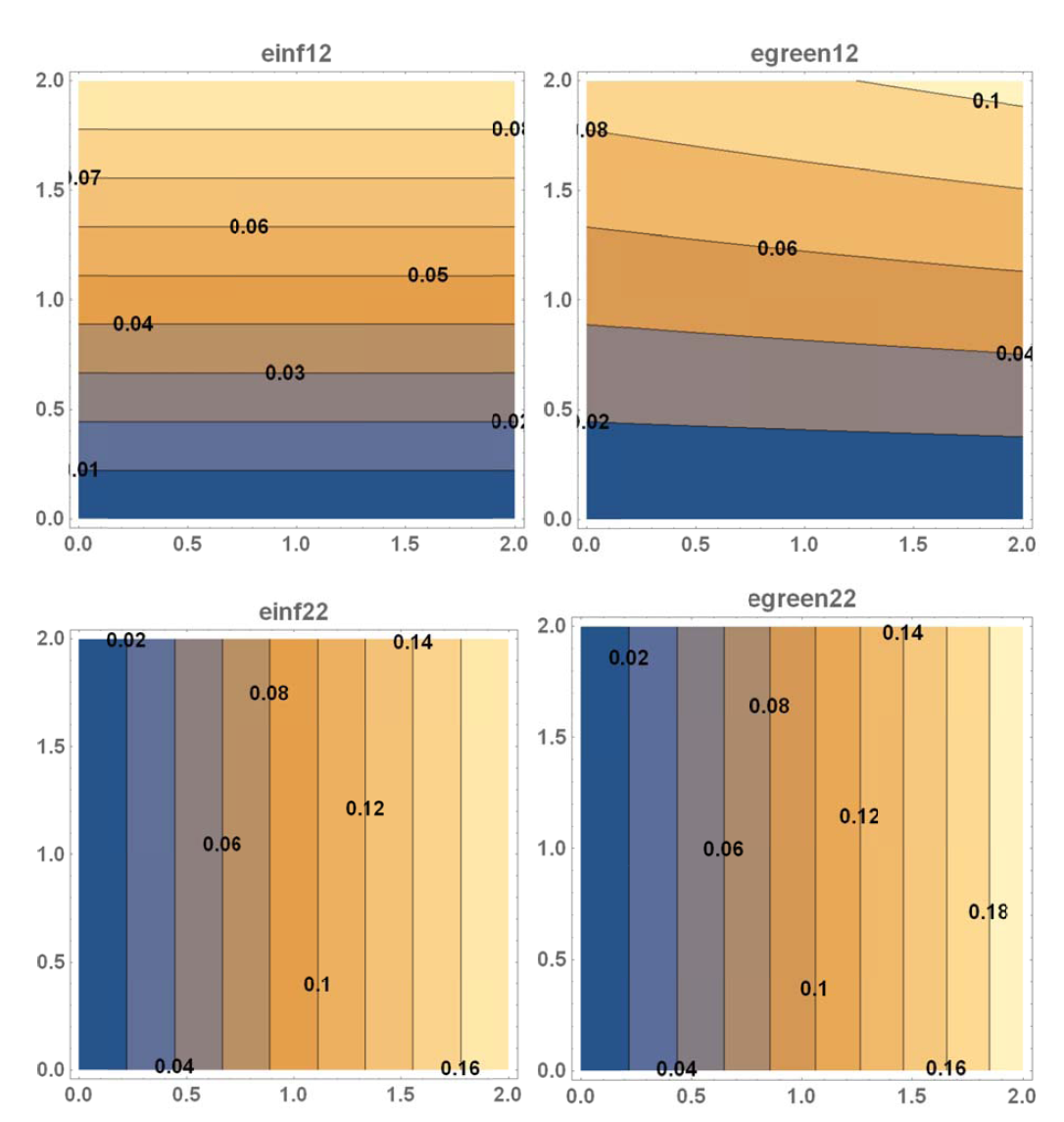
View Mathematica Code
Clear[x1, x2, X1, X2] X = {X1, X2}; u = {0.2 X1, 0.09 X2*X1}; x = u + X; Gradu = Table[D[u[[i]], X[[j]]], {i, 1, 2}, {j, 1, 2}] einfinitesimal = 1/2*(Gradu + Transpose[Gradu]); egreen = 1/2*(Gradu + Transpose[Gradu] + Transpose[Gradu] . Gradu); einfinitesimal // MatrixForm FullSimplify[egreen] // MatrixForm u VectorPlot[u, {X1, 0, 2}, {X2, 0, 2}, BaseStyle -> Directive[Bold, 15], AspectRatio -> Automatic, PlotLabel -> "u"] ContourPlot[einfinitesimal[[1, 1]], {X1, 0, 2}, {X2, 0, 2}, BaseStyle -> Directive[Bold, 15], AspectRatio -> Automatic, ContourLabels -> All, PlotLabel -> "einf11"] ContourPlot[egreen[[1, 1]], {X1, 0, 2}, {X2, 0, 2}, BaseStyle -> Directive[Bold, 15], AspectRatio -> Automatic, ContourLabels -> All, PlotLabel -> "egreen11"] ContourPlot[einfinitesimal[[1, 2]], {X1, 0, 2}, {X2, 0, 2}, BaseStyle -> Directive[Bold, 15], AspectRatio -> Automatic, ContourLabels -> All, PlotLabel -> "einf12"] ContourPlot[egreen[[1, 2]], {X1, 0, 2}, {X2, 0, 2}, BaseStyle -> Directive[Bold, 15], AspectRatio -> Automatic, ContourLabels -> All, PlotLabel -> "egreen12"] ContourPlot[einfinitesimal[[2, 2]], {X1, 0, 2}, {X2, 0, 2}, BaseStyle -> Directive[Bold, 15], AspectRatio -> Automatic, ContourLabels -> All, PlotLabel -> "einf22"] ContourPlot[egreen[[2, 2]], {X1, 0, 2}, {X2, 0, 2}, BaseStyle -> Directive[Bold, 15], AspectRatio -> Automatic, ContourLabels -> All, PlotLabel -> "egreen22"]View Python Code
from sympy import * import sympy as sp from mpl_toolkits.mplot3d import Axes3D import matplotlib.pyplot as plt import numpy as np sp.init_printing(use_latex="mathjax") # calculation X1, X2 = sp.symbols("X_1 X_2") u = Matrix([0.2*X1, 0.09*X2*X1]) display("u =",u) X = Matrix([X1, X2]) x = X + u display("x =", x) F = Matrix([[diff(xi,Xj) for Xj in X] for xi in x]) display("F =",F) grad_u = F - eye(2) display("\u2207u =",grad_u) small_strain = (grad_u+grad_u.T)/2 display("small strain =",small_strain) green_strain = (grad_u+grad_u.T+grad_u.T*grad_u)/2 display("green strain =",green_strain) # plots # vector plots def plotVector(f, limits, title): fx, fy = [lambdify((X1,X2),fi) for fi in f] x1, xn, y1, yn = limits dx, dy = 10/100*(xn-x1),10/100*(yn-y1) xrange = np.arange(x1,xn,dx) yrange = np.arange(y1,yn,dy) X, Y = np.meshgrid(xrange, yrange) dxplot, dyplot = fx(X,Y), fy(X,Y) fig = plt.figure() ax = fig.add_subplot(111) ax.quiver(X, Y, dxplot, dyplot) plt.title(title) # contour plots def plotContour(f, limits, title): x1, xn, y1, yn = limits dx, dy = 10/100*(xn-x1),10/100*(yn - y1) xrange = np.arange(x1,x1+xn,dx) yrange = np.arange(y1,y1+yn,dy) X, Y = np.meshgrid(xrange, yrange) lx, ly = len(xrange), len(yrange) F = lambdify((X1,X2),f) # if F is constant, then generates array # if F generates array, doesn't change anything Z = F(X,Y)*np.ones(lx*ly).reshape(lx, ly) fig = plt.figure() ax = fig.add_subplot(111) cp = ax.contourf(X,Y,Z) fig.colorbar(cp) plt.title(title) # vector plot of u plotVector(u,[0,2,0,2],'u' ) # small strain plots plotContour(small_strain[0,0],[0,2,0,2],'\u03B5_small (1,1)') plotContour(small_strain[0,1],[0,2,0,2],'\u03B5_small (1,2)') plotContour(small_strain[1,1],[0,2,0,2],'\u03B5_small (2,2)') # green strain plots plotContour(green_strain[0,0],[0,2,0,2],'\u03B5_Green (1,1)') plotContour(green_strain[0,1],[0,2,0,2],'\u03B5_Green (1,2)') plotContour(green_strain[1,1],[0,2,0,2],'\u03B5_Green (2,2)')
Problems:
- Which of the following functions describing motion is/are not physically possible and why?
-
Calculate the limits of
 and
and 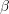 for the following position functions to be physically possible:
for the following position functions to be physically possible:
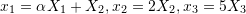 .
.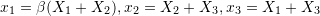 .
.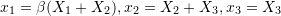 .
.
-
Let a cube of unit length be represented by the set of vectors
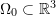 such that three of the cube’s sides are aligned with the three orthonormal basis set vectors
such that three of the cube’s sides are aligned with the three orthonormal basis set vectors 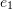 ,
, 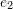 , and
, and 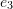 and one of the cube vertices lies on the origin of the coordinate system. Let
and one of the cube vertices lies on the origin of the coordinate system. Let 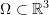 be the deformed configuration such that
be the deformed configuration such that 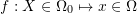 is defined as
is defined as 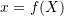 :
:
Find the following:![Rendered by QuickLaTeX.com \[\begin{split} x_1&=1.1X_1+0.02X_1^2+0.01X_2+0.03X_3\\ x_2&=0.001X_1+0.9X_2+0.003X_3\\ x_3&=0.001X_1+0.005X_2+0.009X_3^2+0.9X_3 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a985f927dbb5303a180c7196baf8161b_l3.png)
- The displacement function
 .
. - The new position of the 8 vertices of the cube.
- The deformed curves of the three edges of the cube that are aligned with the basis vectors
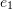 ,
, 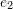 , and
, and 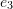 .
. - The infinitesimal strain matrix and the volumetric strain as a function of the position inside the cube.
- The Green strain matrix as a function of the position inside the cube.
- Evaluate the infinitesimal strain matrix at two of the eight cube vertices.
- Evaluate the Green strain matrix at two of the eight cube vertices.
- The displacement function
-
The reference and deformed configurations of an object exhibiting a two dimensional motion
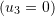 is shown in the figure below.
is shown in the figure below.
Find the following:
- The two dimensional position function that can describe this shown motion.
- The associated two dimensional displacement function. The associated small strain tensor.
- The associated Green Lagrange strain tensor.
-
A cube undergoes a deformation such that the infinitesimal strain is described by the matrix:
Find the following:![Rendered by QuickLaTeX.com \[ \varepsilon_{small}=\left(\begin{matrix}0.015&0.005&0\\0.005&-0.002&0\\0&0&0\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-cc0ee235b7f79dfbf03df413987aa2c8_l3.png)
- The principal strains and their directions.
- The longitudinal strains along the direction of the vector:
![Rendered by QuickLaTeX.com \[ dX=\left(\begin{array}{c}1\\1\\1\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-0f47df42321f249f94ef2472be74d78f_l3.png)
- The approximate change in the angles between the vectors dX and
![Rendered by QuickLaTeX.com \[ dY=\left(\begin{array}{c}-1\\1\\1\end{array}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-535ca83c1a70c55bb524309099000e8f_l3.png)
- The coordinate system transformation in which the strain matrix is diagonal. Express the strain matrix in the new coordinate system.
-
The longitudinal engineering strains on the surface of a test specimen were measured using a strain rosette to be 0.005, 0.002, and –0.001 along the three directions:
 ,
, 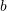 , and
, and 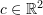 where
where  is along the direction of the basis vector
is along the direction of the basis vector 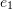 ,
, 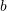 is oriented
is oriented 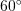 anticlockwise from
anticlockwise from  , and
, and  is oriented
is oriented 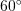 anticlockwise from
anticlockwise from 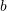 . If the material is assumed to be in a small strain state, find the principal strains and their directions on the surface of the test specimen.
. If the material is assumed to be in a small strain state, find the principal strains and their directions on the surface of the test specimen.
- The longitudinal engineering strains on the surface of a test specimen were measured using a strain rosette to be 0.006, -0.001, and 0.002 along the three directions:
 ,
, 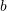 , and
, and 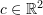 where a is along the direction of the basis vector
where a is along the direction of the basis vector 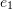 ,
, 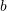 is oriented
is oriented  anticlockwise from
anticlockwise from  , and
, and  is oriented
is oriented 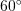 anticlockwise from
anticlockwise from 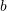 . If the material is assumed to be in a small strain state, find the principal strains and their directions on the surface of the test specimen.
. If the material is assumed to be in a small strain state, find the principal strains and their directions on the surface of the test specimen.
- The measured strains for the three axes of a strain gauge rosette are:
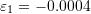 ,
, 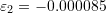 , and
, and 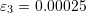 . If
. If  coincides with the basis vector
coincides with the basis vector  while
while  and
and 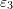 coincide with vectors that are anticlockwise
coincide with vectors that are anticlockwise 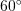 and
and 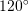 respectively from
respectively from 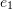 . Find the components of the strain tensor.
. Find the components of the strain tensor.
- Assume that a two dimensional rectangular plate with dimensions 5 units along the basis vector
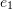 and 1 unit along the basis vector
and 1 unit along the basis vector 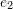 is situated such that the origin of the coordinate system is at the midpoint of the left side of the plate. If the displacement function of the plate is described by:
is situated such that the origin of the coordinate system is at the midpoint of the left side of the plate. If the displacement function of the plate is described by:
find the following:![Rendered by QuickLaTeX.com \[ \begin{split} u_1&=(-0.005X_1^2+0.004X_1)X_2\\ u_2&=-0.00016X_1^3+0.0012X_1^2\\ u_3&=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fd010ffb57d30605a924134f31656da2_l3.png)
- The position function
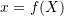 .
. - The infinitesimal strain matrix as a function of the position.
- The Green strain matrix as a function of the position.
- Draw the vector plot of the displacement function.
- Draw the contour plots of
 ,
, 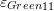 ,
,  , and
, and 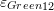 .
.
- The position function
-
Repeat the previous question if the displacement function is given by:
![Rendered by QuickLaTeX.com \[ \begin{split} u_1&=(-0.001X_1^2+0.003X_1)X_2\\ u_2&=(-0.007X_2^2+0.003X_1^2)X_1\\ u_3&=0 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-f00235b5820cadd3db75409416ae8df6_l3.png)
-
The general equation for the coordinates of a point x on an ellipsoidal surface whose axes are oriented along the Cartesian coordinate system is:
where![Rendered by QuickLaTeX.com \[ \left(\frac{x_1}{a}\right)^2+\left(\frac{x_2}{b}\right)^2+\left(\frac{x_3}{c}\right)^2=1 \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-76281f133f3eb3d11422474ab10f6081_l3.png)
 ,
, 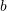 , and
, and  are the three semi-diameters of the ellipsoidal surface. When
are the three semi-diameters of the ellipsoidal surface. When 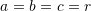 , the surface is a sphere with radius
, the surface is a sphere with radius  . Assuming that the motion of an object is described by the homogeneous deformation gradient
. Assuming that the motion of an object is described by the homogeneous deformation gradient 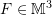 such that the diagonal components of
such that the diagonal components of 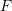 are the only non-zero components.
are the only non-zero components.
- Show that a sphere of radius
 deforms into an ellipsoid surface.
deforms into an ellipsoid surface. - Find the relationship between the semi-diameters of the ellipsoid and the components
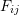 of the deformation gradient.
of the deformation gradient. - Find the relationship between the semi-diameters of the ellipsoid and the components
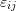 of the infinitesimal strain tensor.
of the infinitesimal strain tensor.
- Show that a sphere of radius
-
Three unit square elements in
 deform as shown in the figure below.
deform as shown in the figure below.
For each case: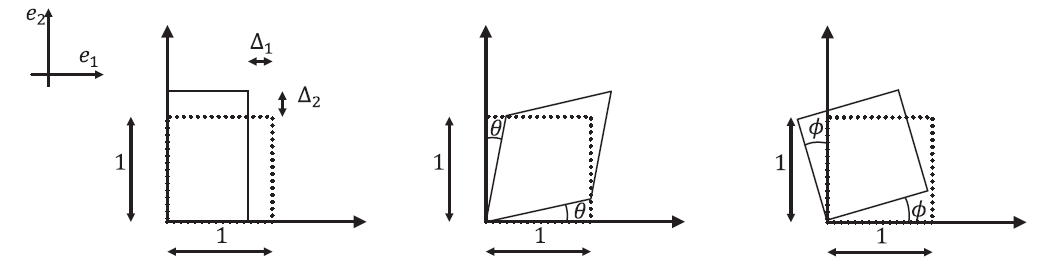
- Write expressions for the displacement components
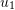 and
and 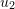 as functions of
as functions of  ,
, 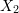 , and the variables shown for each square.
, and the variables shown for each square. - Determine the components of the infinitesimal strain tensor and the infinitesimal rotation tensor.
- Determine the components of the Green strain tensor.
- Write expressions for the displacement components
