Open Educational Resources

Plasticity: FEA Implementation

Implementation in FEA

In order to implement the nonlinear material models of plasticity described before in a finite element analysis algorithm, the overall stiffness describing the rate of change of the stress increments with respect to the strain increments is required. In particular, the components of the following fourth order tensor are required for implementation in a Newton Raphson method:

    \[\frac{\partial \sigma}{\partial \varepsilon} = \frac{\dot{\sigma}}{\dot{\varepsilon}}\]

where \sigma is the stress tensor and \varepsilon is the total strain tensor. In order to find the components of this fourth order tensor, the incremental form of the stress-strain relationships in the Mathematical Modelling of Plasticity section are utilized. This is done for both models, the isotropic hardening model and the combined isotropic and kinematic hardening model. Note that in the derivations in the coming section, replacing \Delta\sigma_{ij} with \dot{\sigma}_{ij} and \Delta\varepsilon_{ij} with \dot{\varepsilon}_{ij} will yield the same results.

Incremental Stress-strain Relationships for the Isotropic Hardening Model

Adopting a vector representation of the stress and the strain increments, the increments in the stress, strain, elastic strain and plastic strain components can be represented as elements of a six dimensional vector space with the following components:

    \[\Delta \sigma, \Delta \varepsilon, \Delta \varepsilon^e, \Delta \varepsilon^p \in \mathbb{R}^6\]

    \[\Delta \sigma = \begin{pmatrix} \Delta \sigma_{11} \\ \Delta \sigma_{22} \\ \Delta \sigma_{33} \\ \Delta \sigma_{12} \\ \Delta \sigma_{13} \\ \Delta \sigma_{23} \\ \end{pmatrix} \hspace{5mm} \Delta \varepsilon = \begin{pmatrix} \Delta \varepsilon_{11} \\ \Delta \varepsilon_{22} \\ \Delta \varepsilon_{33} \\ \Delta \varepsilon_{12} \\ \Delta \varepsilon_{13} \\ \Delta \varepsilon_{23} \\ \end{pmatrix} \hspace{5mm} \Delta \varepsilon^e = \begin{pmatrix} \Delta \varepsilon_{11}^e \\ \Delta \varepsilon_{22}^e \\ \Delta \varepsilon_{33}^e \\ \Delta \varepsilon_{12}^e \\ \Delta \varepsilon_{13}^e \\ \Delta \varepsilon_{23}^e \\ \end{pmatrix} \hspace{5mm} \Delta \varepsilon^p = \begin{pmatrix} \Delta \varepsilon_{11}^p \\ \Delta \varepsilon_{22}^p \\ \Delta \varepsilon_{33}^p \\ \Delta \varepsilon_{12}^p \\ \Delta \varepsilon_{13}^p \\ \Delta \varepsilon_{23}^p \\ \end{pmatrix}\]

When a stress increment is such that plastic strain would develop in the material, then the vector of the increments in the strain components is equal to the sum of the incremental elastic and the plastic strain components:

    \[\Delta f = \Delta \sigma_{vM} - \Delta \sigma_Y = \sum_{i,j=1}^3 \frac{\partial \sigma_{vM}}{\partial \sigma_{ij}} \Delta \sigma_{ij} - \frac{d \sigma_Y}{d \overline{\varepsilon^p}} \Delta \overline{\varepsilon^p} = 0 \Rightarrow \Delta \varepsilon = \Delta \varepsilon^e + \Delta \varepsilon^p\]

Denoting h=\frac{d\sigma_{Y}}{d\overline{\varepsilon^p}}, the above relationship can also be used to find an expression for \Delta\overline{\varepsilon^p}:

    \[\Delta \overline{\varepsilon^p} = \frac{1}{h} \sum_{i,j=1}^3 \frac{\partial \sigma_{vM}}{\partial \sigma_{ij}} \Delta \sigma_{ij}\]

The incremental elastic strain components are related to the increment in the stress components using the linear elastic constitutive behaviour:

    \[\Delta \varepsilon_{ij}^e = \frac{1+\nu}{E} \Delta \sigma_{ij} - \frac{\nu \delta_{ij}}{E} \sum_{k=1}^3 \Delta \sigma_{kk}\]

which has the following matrix form:

    \[\begin{pmatrix} \Delta \varepsilon_{11}^e \\ \Delta \varepsilon_{22}^e \\ \Delta \varepsilon_{33}^e \\ \Delta \varepsilon_{12}^e \\ \Delta \varepsilon_{13}^e \\ \Delta \varepsilon_{23}^e \\ \end{pmatrix} = \frac{1}{E} \begin{pmatrix} 1 & -\nu & -\nu & 0 & 0 & 0 \\ -\nu & 1 & -\nu & 0 & 0 & 0 \\ -\nu & -\nu & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1+\nu & 0 & 0 \\ 0 & 0 & 0 & 0 & 1+\nu & 0 \\ 0 & 0 & 0 & 0 & 0 & 1+\nu \\ \end{pmatrix} \begin{pmatrix} \Delta \sigma_{11} \\ \Delta \sigma_{22} \\ \Delta \sigma_{33} \\ \Delta \sigma_{12} \\ \Delta \sigma_{13} \\ \Delta \sigma_{23} \\ \end{pmatrix}\]

The incremental plastic strain components are related to the increment in the stress components as follows after incorporating the von Mises yield function, flow rule and hardening rule:

    \[\Delta \varepsilon_{ij}^p = \Delta \overline{\varepsilon^p} \frac{\partial f}{\partial \sigma_{ij}} = \frac{1}{h} \sum_{k,l=1}^3 \frac{\partial \sigma_{vM}}{\partial \sigma_{kl}} \Delta \sigma_{kl} \frac{\partial f}{\partial \sigma_{ij}} = \frac{9S_{ij}}{4h\sigma_{vM}^2} \sum_{k,l=1}^3 S_{kl} \Delta \sigma_{kl}\]

Which has the following component form:

    \[\begin{pmatrix} \Delta \varepsilon_{11}^p \\ \Delta \varepsilon_{22}^p \\ \Delta \varepsilon_{33}^p \\ \Delta \varepsilon_{12}^p \\ \Delta \varepsilon_{13}^p \\ \Delta \varepsilon_{23}^p \\ \end{pmatrix} = \frac{9}{h \sigma_{vM}^2} \begin{pmatrix} S_{11}S_{11} & S_{11}S_{22} & S_{11}S_{33} & 2S_{11}S_{12} & 2S_{11}S_{13} & 2S_{11}S_{23} \\ S_{22}S_{11} & S_{22}S_{22} & S_{22}S_{33} & 2S_{22}S_{12} & 2S_{22}S_{13} & 2S_{22}S_{23} \\ S_{33}S_{11} & S_{33}S_{22} & S_{33}S_{33} & 2S_{33}S_{12} & 2S_{33}S_{13} & 2S_{33}S_{23} \\ S_{12}S_{11} & S_{12}S_{22} & S_{12}S_{33} & 2S_{12}S_{12} & 2S_{12}S_{13} & 2S_{12}S_{23} \\ S_{13}S_{11} & S_{13}S_{22} & S_{13}S_{33} & 2S_{13}S_{12} & 2S_{13}S_{13} & 2S_{13}S_{23} \\ S_{23}S_{11} & S_{23}S_{22} & S_{23}S_{33} & 2S_{23}S_{12} & 2S_{23}S_{13} & 2S_{23}S_{23} \\ \end{pmatrix} \begin{pmatrix} \Delta \sigma_{11} \\ \Delta \sigma_{22} \\ \Delta \sigma_{33} \\ \Delta \sigma_{12} \\ \Delta \sigma_{13} \\ \Delta \sigma_{23} \\ \end{pmatrix}\]

where h=\frac{d\sigma_Y}{d\overline{\varepsilon^p}} is the slope of the material yield stress versus plastic strain curve and the factor 2 accounts for the symmetry of the stress tensor increments (\Delta \sigma_{12}=\Delta\sigma_{21}). The relationships above can be written in the following form where D=D^e+D^p represents the inverse of the material stiffness in the current stress increment:

    \[\Delta \varepsilon = \Delta \varepsilon^e + \Delta \varepsilon^p = (D^e + D^p) \Delta \sigma = D \Delta \sigma\]

In the case the case of elastic perfectly plastic materials, the value of h is zero and the increments in the stress have to satisfy the condition that \sigma_{vM}=\sigma_Y where \sigma_Y is constant. In this case, the increment in the plastic strain parameter \Delta\overline{\varepsilon^p} is not well defined (could be infinite) and more conditions (kinematic conditions) would be required to obtain the plastic strain components. In the case of a finite value for h, the inverse relationship is required for implementation in the Newton Raphson method (i.e., the inverse of D). The inverse can be obtained numerically after constructing the matrices or explicitly as follows. First, the increments in the total strain components can be written in the following form:

    \[\Delta \varepsilon_{ij} = \Delta \varepsilon^e + \Delta \varepsilon^p = \frac{1+\nu}{E} \Delta \sigma_{ij} - \frac{\nu \delta_{ij}}{E} \sum_{k=1}^3 \Delta \sigma_{kk} + \frac{9S_{ij}}{4h \sigma_{vM}^2} \sum_{k,l=1}^3 S_{kl} \Delta \sigma_{kl}\]

In order to find the inverse of the above relationship, we first start by rearranging as follows:

(1)   \begin{equation*} \Delta \sigma_{ij} = \frac{E}{1+\nu} \Delta \varepsilon_{ij} + \frac{\nu \delta_{ij}}{1+\nu} \sum_{k=1}^3 \Delta \sigma_{kk} - \frac{E}{(1+\nu)} \frac{9S_{ij}}{4h\sigma_{vM}^2} \sum_{k,l=1}^3 S_{kl} \Delta \sigma_{kl} \end{equation*}

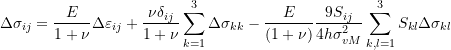
In the following steps, we wish to replace the components of the stress increment \Delta \sigma in the right hand side with the components of the strain increment \Delta\varepsilon. To achieve this, first, we note that if the deviatoric stress tensor components are multiplied by the increments of the total strain components and then the resulting terms are summed (i.e., obtaining the inner product of the deviatoric stress tensor and the increment in the total strain tensor), then the following expressions are obtained:

    \[\sum_{i,j=1}^3 S_{ij} \Delta \varepsilon_{ij} = \sum_{i,j=1}^3 S_{ij} (\Delta \varepsilon_{ij}^e + \Delta \varepsilon_{ij}^p)\]

The first term with the deviatoric stress tensor components multiplied by the incremental elastic strain components can be further manipulated as follows:

    \[\sum_{i,j=1}^3 S_{ij} \Delta \varepsilon_{ij}^e = \sum_{i,j=1}^3 \frac{1+\nu}{E} S_{ij} \Delta \sigma_{ij} - \frac{\nu}{E} \sum_{k=1}^3 S_{kk} \sum_{l=1}^3 \Delta \sigma_{u}\]

The second term equals to zero since the trace of the deviatoric stress tensor is equal to zero.
On the other hand, the term with the deviatoric stress tensor components multiplied by the incremental plastic strain components can be further manipulated as follows:

    \[\sum_{i,j=1}^3 S_{ij} \Delta \varepsilon_{ij}^p = \sum_{i,j=1}^3 \frac{9S_{ij}S_{ij}}{4h\sigma_{vM}^2} \sum_{k,l=1}^3 S_{kl} \Delta \sigma_{kl} = \frac{3}{2h} \sum_{k,l=1}^3 S_{kl} \Delta \sigma_{kl}\]

Therefore:

    \[\sum_{i,j=1}^3 S_{ij} \Delta \varepsilon_{ij} = \Big(\frac{1+\nu}{E} + \frac{3}{2h} \Big) \sum_{i,j=1}^3 S_{ij} \Delta \sigma_{ij}\]

Substituting back into the third term of equation 1 results in:

    \[\Delta \sigma_{ij} = \frac{E}{1+\nu} \Delta \varepsilon_{ij} + \frac{\nu \delta_{ij}}{1+\nu} \sum_{k=1}^3 \Delta \sigma_{kk} - \frac{E}{(1+\nu)} \frac{9S_{ij}}{4h\sigma_{vM}^2} \sum_{k,l=1}^3 \frac{2hE}{2(1+\nu)h + 3E} S_{kl} \Delta \varepsilon_{kl}\]

Finally, the middle term \Delta\sigma_{kk} can be replaced knowing that the incremental volumetric total strain is equal to the incremental volumetric elastic strain since the incremental volumetric plastic strain is equal to zero:

    \[\sum_{k=1}^3 \Delta \varepsilon_{kk} = \sum_{k=1}^3 \Delta \varepsilon_{kk}^e = \frac{1-2\nu}{E} \sum_{k=1}^3 \Delta \sigma_{kk}\]

Therefore, the final incremental stress total strain relationship has the following form:

    \[\Delta \sigma_{ij} = \frac{E}{1+\nu} \Delta \varepsilon_{ij} + \frac{\nu E \delta_{ij}}{(1+\nu)(1-2\nu)} \sum_{k=1}^3 \Delta \varepsilon_{kk} - \frac{9E^2S_{ij}}{2(1+\nu)\sigma_{vM}^2 (2(1+\nu)h+3E)} \sum_{k,l=1}^3 S_{kl} \Delta \varepsilon_{kl}\]

The shear modulus G=\frac{E}{2(1+\nu)} can be used to further simplify the relationship as follows.

    \[\Delta \sigma_{ij} = 2G \Big(\Delta \varepsilon_{ij} + \frac{\nu \delta_{ij}}{(1-2\nu)} \sum_{k=1}^3 \Delta \varepsilon_{kk} - \frac{9S_{ij}G}{2\sigma_{vM}^2(h+3G)} \sum_{k,l=1}^3 S_{kl} \Delta \varepsilon_{kl}\Big)\]

Notice that this relationship can still be utilized to find the increments in the stress components if h=0 (elastic perfectly plastic materials). In this case, if the increments in the total strain components are known, the associated increments in the stress components can be obtained. These increments in the stress components will ensure that \sigma_{vM} does not increase since in elastic perfectly plastic material, \sigma_Y is constant. The details of this argument are shown below. When h=0, we have:

    \[\Delta f = \Delta \sigma_{vM} - \Delta \sigma_{Y} = \sum_{i,j=1}^3 \frac{\partial \sigma_{vM}}{\partial \sigma_{ij}} \Delta \sigma_{ij} - \frac{d\sigma_Y}{d \overline{\varepsilon^p}} \Delta \overline{\varepsilon^p} = \sum_{i,j=1}^3 \frac{\partial \sigma_{vM}}{\partial \sigma_{ij}} \Delta \sigma_{ij} - h \Delta \overline{\varepsilon^p} = \sum_{i,j=1}^3 \frac{\partial \sigma_{vM}}{\partial \sigma_{ij}} \Delta \sigma_{ij}\]

By substituting for \Delta\sigma_{ij} in the above equation we reach that \Delta\sigma_{vM}=0 as follows:

    \[\Delta \sigma_{vM} = \sum_{i,j=1}^3 \frac{3S_{ij}}{2\sigma_{vM}} \Delta \sigma_{ij} = \frac{3G}{\sigma_{vM}} \sum_{\i,j=1}^3 \Big(S_{ij} \Delta \varepsilon_{ij} - \frac{3S_{ij}S_{ij}}{2\sigma_{vM}^2} \sum_{k,l=1}^3 S_{kl} \Delta \varepsilon_{kl} \Big)\]

    \[= \frac{3G}{\sigma_{vM}} \Big(\sum_{i,j=1}^3 S_{ij} \Delta \varepsilon_{IJ} - \sum_{i,j=1}^3 S_{kl} \Delta \varepsilon_{kl} \Big) = 0\]

Incremental Stress-strain Relationships for the Combined Kinematic and Isotropic Hardening Model

We first recall the relationships for this material model:

(2)   \begin{equation*} \Delta \alpha_{ij} = \Big(\frac{C(\sigma_{ij} - \alpha_{ij})}{\sigma_{Y \alpha}} - \gamma \alpha_{ij} \Big) \Delta \overline{\varepsilon^p} \end{equation*}

where \alpha_{ij} are the components of the backstress tensor.

The incremental form of the consistency condition is:

    \[\Delta f = \sum_{i,j=1}^3 \frac{\partial f}{\partial \sigma_{ij}} \Delta \sigma_{ij} + \sum_{i,j=1}^3 \frac{\partial f}{\partial \alpha_{ij}} \Delta \alpha_{ij} - \frac{d \sigma_{Y \alpha}}{d \overline{\varepsilon^p}} \Delta \overline{\varepsilon^p} = 0\]

With

    \[\frac{\partial f}{\partial \sigma_{ij}} = -\frac{\partial f}{\partial \alpha_{ij}} = \frac{\frac{3}{2}(S_{ij} - \alpha_{ij}^{dev})}{\sigma_{vM}|_{\sigma - \alpha}}\]

Denoting

    \[h = \frac{d \sigma_{Y \alpha}}{d \overline{\varepsilon^p}} \hspace{5mm} M_{ij} = \Big(\frac{C(\sigma_{ij} - \alpha_{ij})}{\sigma_{Y \alpha}} - \gamma \alpha_{ij} \Big)\]

and by substituting for the components of the backstress tensor in the consistency condition equation using Equation 2 we obtain:

    \[\sum_{i,j=1}^3 \frac{\partial f}{\partial \sigma_{ij}} \Delta \sigma_{ij} - \Big(\sum_{i,j=1}^3 \frac{\partial f}{\partial \sigma_{ij}} M_{ij} + h \Big) \Delta \overline{\varepsilon^p} = 0\]

Denoting

    \[h_{\alpha} = \sum_{i,j=1}^3 \frac{\partial f}{\partial \sigma_{ij}} M_{ij} + h\]

then, the consistency condition is simplified to the following form:

    \[\sum_{i,j=1}^3 \frac{\partial f}{\partial \sigma_{ij}} \Delta \sigma_{ij} - h_{\alpha} \Delta \overline{\varepsilon^p} = 0\]

The increments in the plastic strain tensor components can now be written as:

    \[\Delta \varepsilon_{ij}^p = \Delta \overline{\varepsilon^p} \frac{\partial f}{\partial \sigma_{ij}} = \Delta \overline{\varepsilon^p} \Big(\frac{\frac{3}{2}(S_{ij} - \alpha_{ij}^{dev})}{\sigma_{vM}|_{\sigma - \alpha}} \Big) = \Big(\frac{\frac{3}{2}(S_{ij} - \alpha_{ij}^{dev})}{h_{\alpha}\sigma_{vM}|_{\sigma-\alpha}} \Big) \sum_{k,l=1}^3 \frac{\partial f}{\partial \sigma_{kl}} \Delta \sigma_{kl}\]

    \[= \Big(\frac{\frac{3}{2}(S_{ij} - \alpha_{ij}^{dev})}{h_{\alpha} \sigma_{vM}|_{\sigma - \alpha}} \Big) \sum_{k,l=1}^3 \frac{\frac{3}{2}(S_{kl} - \alpha_{kl}^{dev})}{\sigma_{vM}|_{\sigma - \alpha}} \Delta \sigma_{kl}\]

Using the elastic stress strain relationships shown in the previous section and substituting the above equation in the equation \varepsilon_{ij}=\varepsilon_{ij}^e+\varepsilon_{ij}^p yields the following relationship between the increments in the total strain and those of the stress:

    \[\Delta \varepsilon_{ij} = \Delta \varepsilon^e + \Delta \varepsilon^p = \frac{1+\nu}{E} \Delta \sigma_{ij} - \frac{\nu \delta_{ij}}{E} \sum_{k=1}^3 \Delta \sigma_{kk} + \Big(\frac{\frac{9}{4}(S_{ij} - \alpha_{ij}^{dev})}{h_{\alpha} \sigma_{vM}^2|_{\sigma - \alpha}} \Big) \sum_{k,l=1}^3 \frac{3}{2} (S_{kl} - \alpha_{kl}^{dev}) \Delta \sigma_{kl}\]

Rearranging:

(3)   \begin{equation*} \Delta \sigma_{ij} = \frac{E}{1+\nu} \Delta \varepsilon_{ij} + \frac{\nu \delta_{ij}}{1+\nu} \sum_{k=1}^3 \Delta \sigma_{kk} - \frac{E}{(1+\nu)}\frac{9(S_{ij}-\alpha_{ij}^{dev})} {4h_{\alpha} \sigma_{vM}^2 |_{\sigma - \alpha}} \sum_{k,l=1}^3 (S_{kl} - \alpha_{kl}^{dev}) \Delta \sigma_{kl} \end{equation*}

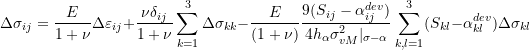
Similar to the derivation for the above section, the inner production between S-\alpha^{dev} and \varepsilon is obtained as follows:

    \[\sum_{i,j=1}^3 (S_{ij} - \alpha_{ij}^{dev}) \Delta \varepsilon_{ij} = \sum_{i,j=1}^3 (S_{ij} - \alpha_{ij}^{dev})(\Delta \varepsilon_{ij}^e + \Delta \varepsilon_{ij}^p)\]

The first term can be further manipulated as follows:

    \[\sum_{i,j=1}^3 (S_{ij} - \alpha_{ij}^{dev}) \Delta \varepsilon_{ij}^e = \sum_{i,j=1}^3 \frac{1+\nu}{E} (S_{ij} - \alpha_{ij}^{dev}) \Delta \sigma_{ij} - \frac{\nu}{E} \sum_{k=1}^3 (S_{kk} - \alpha_{kk}^{dev}) \sum_{l=1}^3 \Delta \sigma_u\]

The second term equals to zero since the trace of S-\alpha^{dev} is equal to zero. On the other hand, the term with the deviatoric stress tensor components multiplied by the incremental plastic strain components can be further manipulated as follows:

    \[\sum_{i,j=1}^3 (S_{ij} - \alpha_{ij}^{dev}) \Delta \varepsilon_{ij}^p = \sum_{i,j=1}^3 \frac{9(S_{ij} - \alpha_{ij}^{dev})(S_{ij} - \alpha_{ij}^{dev})} {4h_{\alpha}\sigma_{vM}^2|_{\sigma - \alpha}} \sum_{k,l=1}^3 (S_{kl} - \alpha_{kl}^{dev}) \Delta \sigma_{kl}\]

    \[= \frac{3}{2h_{\alpha}} \sum_{k,l=1}^3 (S_{kl} - \alpha_{kl}^{dev}) \Delta \sigma_{kl}\]

Therefore:

    \[\sum_{i,j=1}^3 (S_{ij} - \alpha_{ij}^{dev}) \Delta \varepsilon_{ij} = \Big(\frac{1+\nu}{E} + \frac{3}{2h_{\alpha}}\Big) \sum_{i,j=1}^3 (S_{ij} - \alpha_{ij}^{dev}) \Delta \sigma_{ij}\]

Substituting back into the third term of equation 3 results in:

    \[\Delta \sigma_{ij} = \frac{E}{1+\nu} \Delta \varepsilon_{ij} + \frac{\nu \delta_{ij}}{1+\nu} \sum_{k=1}^3 \Delta \sigma_{kk} - \frac{E}{(1+\nu)} \frac{9(S_{ij} - \alpha_{ij}^{dev})}{4h_{\alpha} \sigma_{vM}^2|_{\sigma - \alpha}} \sum_{k,l=1}^3 \frac{2h_{\alpha}E}{2(1+\nu)h_{\alpha} + 3E}(S_{kl} - \alpha_{kl}^{dev}) \Delta \varepsilon_{kl}\]

Similar to the derivation in the previous section, \sum_{k=1}^3\Delta\sigma_{kk}=\frac{E}{(1-2\nu)} \sum_{k=1}^3\Delta\varepsilon_{kk} which can be used to reach the final relationship:

    \[\Delta \sigma_{ij} = \frac{E}{1+\nu} \Delta \varepsilon_{ij} + \frac{\nu E \delta_{ij}}{(1+\nu)(1-2\nu)} \sum_{k=1}^3 \Delta \varepsilon_{kk}\]

    \[- \frac{9E^2h_{\alpha}}{(1+\nu)(2(1+\nu)h_{\alpha}+3E)} \frac{(S_{ij} - \alpha_{ij}^{dev})}{4H_{\alpha}\sigma_{vM}^2|_{\sigma - \alpha}} \sum_{k,l=1}^3 (S_{kl} - \alpha_{kl}^{dev}) \Delta \varepsilon_{kl}\]

Leave a Reply

Your email address will not be published.