Engineering at Alberta Courses » First and Second Piola Kirchhoff Stress Tensors

Stress: First and Second Piola Kirchhoff Stress Tensors

Definitions

The Cauchy stress tensor defined previously, related area vectors n to traction vectors $t_n$ in the current state of deformation of a material object. The first and second Piola-Kirchhoff stress tensors extend the concept of “true” and “engineering” stress to the three-dimensional case and operate on area vectors in the undeformed state of the material. Assume that the area vector before any forces are applied to a continuum is equal to $(A)N$ where $A \in\mathbb{R}$ is the magnitude of the area and $N\in\mathbb{R}^3$ is the vector perpendicular to the underformed area. Assume that the forces applied lead to a deformation described by the linear mapping $F \in\mathbb{M}^3$ such that $F=\frac{\partial f}{\partial X}$ where $f:X\in\Omega_0\mapsto x\in\Omega$ . Let the area vector after deformation be $(a)n$ where $a\in\mathbb{R}$ is the magnitude of the deformed area and $n\in\mathbb{R}^3$ is the vector perpendicular to the deformed area. Then, using Nanson’s formula:

$(a)n = \det(F)(A)F^{-T}N$

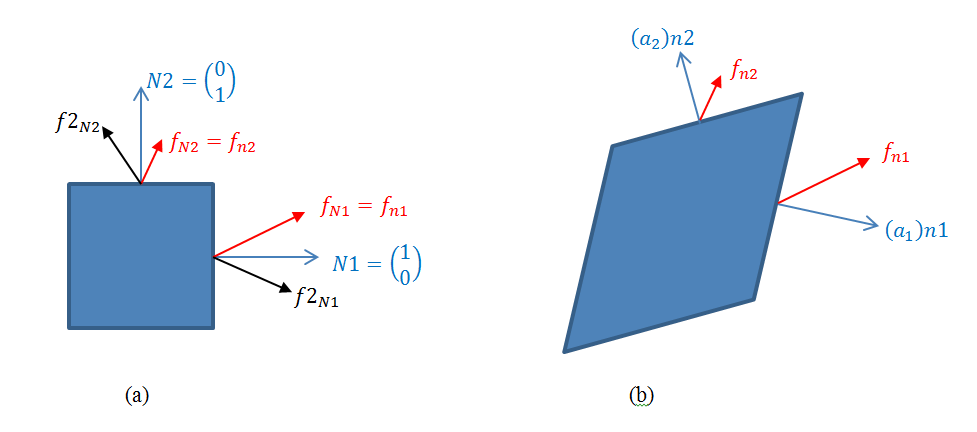
The blue vectors in Figure 1 show a schematic of two undeformed unit area vectors $N1$ and $N2 (A=1)$ and their respective images $(a_1)n1$ and $(a_2)n2$ after transformation by a linear mapping $F$ . After deformation, the force vector acting on an area with normal $n$ and magnitude $a$ is equal to $f_n =(a)t_n=(a)\sigma^Tn\in\mathbb{R}^3$ . The first Piola-Kirchhoff stress tensor $P$ is defined as the tensor producing the same force vector $f_n$ when applied to the corresponding undeformed area vector $(A)N$ :

$f_N = f_n = (A)PN$

Using Nanson’s formula:

$(A)PN = (a)\sigma^Tn = \det(F)(A)\sigma^TF^{-T}N$

Therefore,

$PN = \det(F)\sigma^TF^{-T}N$

Which results in the following relationship between $P$ and $\sigma$ :

$P = \det(F)\sigma^TF^{-T}$

Note that the above relationship indicates that $P$ is not necessarily a symmetric matrix. The term “Nominal Stress Tensor” is sometimes used in the literature in reference to the first Piola-Kirchhoff stress or its transpose. The red vectors in Figure 1 show a schematic of the forces acting on the deformed area vectors $(a_1)n1$ and $(a_2)n2$ when viewed in the deformed configuration or when viewed in the undeformed configuration. On the other hand, the second Piola-Kirchhoff stress tensor $S$ is defined as the tensor producing a force vector $f2_N=F^{-1}f_n$ when applied to the undeformed area vector $(A)N$ . $f2_N$ is sometimes termed the “pull-back” of the force vector $f_n$ . The relationship between $S$ and $\sigma^T$ can be obtained as follows:

$f2_N = (A)SN = F^{-1}f_n = (a)F^{-1}\sigma^Tn$

Therefore:

$(A)SN = (a)F^{-1}\sigma^Tn$

Using Nanson’s formula:

$(A)SN = (A)\det (F)F^{-1} \sigma^T F^{-T}N$

Which results in the following relationship between $S$ and $\sigma$ :

$S = \det(F)F^{-1}\sigma^T F^{-T}$

Therefore S is a symmetric tensor!

Notice that the relationship between $S$ and $P$ is:

$S = F^{-1}P$

The black vectors in Figure 1 show a schematic of the $f2_{N1}$ and $f2_{N2}$ which are the “pull-back” of the force vectors $f_{n1}$ and $f_{n2}$ .

Figure 1. The force and area vectors on (a) the undeformed configuration, and (b) the deformed configuration.

The illustrative examples 1, 2, and 3 in the energy section can help clarify the difference between the three major stress tensors.

Example

Consider $\mathbb{R}^2$ . Assume that a region inside a material deforms with the following deformation gradient $F$ :

$F = \begin{pmatrix} 1.2 & 0.4 \\ 0.4 & 1.2 \\ \end{pmatrix}$

Assume that the stress in the deformed configuration is described by the matrix:

$\sigma = \begin{pmatrix} 5 & 2 \\ 2 & 3 \\ \end{pmatrix}$

Find:

The area vectors after deformation of the two original unit areas with area vectors 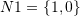$N1=\{1,0\}$ and $N2=\{0,1\}$ .
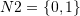The first and second Piola-Kirchhoff stress matrices.
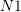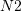The force vectors on the deformed planes whose undeformed unit area vectors are $N1$ and $N2$ using the Cauchy stress matrix.
The force vectors produced by applying the first Piola-Kirchhoff stress tensor on the undeformed unit area vectors 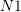$N1$ and $N2$ .
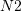The force vectors produced by applying the second Piola-Kirchhoff stress tensor on the undeformed unit area vectors 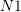$N1$ and $N2$ .

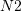Solution

Using Nanson’s formula (with $A=1$ ):

$(a_1)n1 = \det(F)(A)F^{-T}N1 = \begin{pmatrix} 1.2 \\ -0.4 \\ \end{pmatrix}$

$(a_2)n2 = \det(F)(A)F^{-T}N2 = \begin{pmatrix} -0.4 \\ 1.2 \\ \end{pmatrix}$

Where $a_1$ and $a_2$ are the magnitudes of the “deformed” areas and $n1$ and $n2$ are the corresponding normal vectors to the areas whose original normal vectors before deformation are $N1$ and $N2$ , respectively. The first and second Piola-Kirchhoff stress matrices $P$ and $S$ are:

$P = \det(F)\sigma^TF^{-1} = \begin{pmatrix} 5.2 & 0.4 \\ 1.2 & 2.8 \\ \end{pmatrix}$

$S = F^{-1}P = \begin{pmatrix} 4.5 & -0.5 \\ -0.5 & 2.5 \\ \end{pmatrix}$

The force vectors on the deformed area vectors $(a_1)n1$ and $(a_2)n2$ are:

$f_{n1} = (a_1)t_{n1} = (a_1)\sigma^T(n1) = \begin{pmatrix} 5.2 \\ 1.2 \\ \end{pmatrix}$

$f_{n2} = (a_2)t_{n2} = (a_2)\sigma^T(n2) = \begin{pmatrix} 0.4 \\ 2.8 \\ \end{pmatrix}$

The force vectors on the original (undeformed) area vectors $N1$ and $N2$ obtained using the first Piola-Kirchoff stress are exactly the same ( $A=1$ ):

$f_{N1} = (A)P(N1) = \begin{pmatrix} 5.2 \\ 1.2 \\ \end{pmatrix}$

$f_{N2} = (A)P(N2) = \begin{pmatrix} 0.4 \\ 2.8 \\ \end{pmatrix}$

The force vectors on the original area vectors $N1$ and $N2$ when using the Second Piola-Kirchhoff stress ( $A=1$ ):

$f2_{N1} = (A)S(N1) = \begin{pmatrix} 4.5 \\ -0.5 \\ \end{pmatrix}$

$f2_{N2} = (A)S(N2) = \begin{pmatrix} -0.5 \\ 2.5 \\ \end{pmatrix}$

Notice that $f2_{N1}=F^{-1}f_{n1}$ and $f2_{N2}=F^{-1}f_{n2}$ . Figure 1 shows the deformation of an originally square object of unit length and the corresponding deformation of areas. The force vectors are also shown on the different areas before and after deformation. The Cauchy stress and the first Piola-Kirchhoff stress tensors produce the same force vectors. The Cauchy stress matrix can intuitively be viewed as the force in the deformed configuration per unit area of the deformed configuration. The first Piola-Kirchhoff stress matrix can intuitively be viewed as the force in the deformed configuration per unit area of the undeformed configuration, while the second Piola-Kirchhoff stress can intuitively be viewed as the force in the undeformed configuration per unit area of the undeformed configuration. Notice that all these stress measures are equivalent, but they are useful for different applications.

View Mathematica Code

F={{1.2,0.4},{0.4,1.2}};
Bx=Rectangle[{0,0}];
Bx2=GeometricTransformation[Bx,F];
Sigma={{5,2},{2,3}};
N1={1,0};
N2={0,1};
Farea=Det[F]*Transpose[Inverse[F]];
an1=Farea.N1;
an2=Farea.N2;
tn1=Transpose[Sigma].an1
tn2=Transpose[Sigma].an2
FirstPiola=Transpose[Sigma].Inverse[Transpose[F]]*Det[F];
SecondPiola=Inverse[F].FirstPiola;
TN1=FirstPiola.N1;
TN2=FirstPiola.N2;
STN1=SecondPiola.N1;
STN2=SecondPiola.N2;
Pt11=F.N1+1/2*F.N2;
Pt12=Pt11+an1;
Pt21=1/2*F.N1+F.N2;
Pt22=Pt21+an2;
ar1=Arrow[{Pt11,Pt12}];
ar2=Arrow[{Pt21,Pt22}];
A1dotted=Arrow[{Pt11,Pt11+{1,0}}];
A2dotted=Arrow[{Pt21,Pt21+{0,1}}];
A1=Arrow[{{1,0.5},{2,0.5}}];
A2=Arrow[{{0.5,1},{0.5,2}}];
artn1=Arrow[{Pt11,Pt11+1/10*tn1}];
artn2=Arrow[{Pt21,Pt21+1/10*tn2}];
arTN1=Arrow[{{1,0.5},{1,0.5}+1/10*TN1}];
arTN2=Arrow[{{0.5,1},{0.5,1}+1/10*TN2}];
arSTN1=Arrow[{{1,0.5},{1,0.5}+1/10*STN1}];
arSTN2=Arrow[{{0.5,1},{0.5,1}+1/10*STN2}];
Graphics[{Black,Bx,A1,A2,GrayLevel[0.1],arTN1,arTN2,GrayLevel[0.5],arSTN1,arSTN2}]
Graphics[{Black,Bx2,ar1,ar2,GrayLevel[0.1],artn1,artn2,Dashed,GrayLevel[0.5],A1dotted,A2dotted}]

View Python Code

from sympy import Matrix
import sympy as sp
from matplotlib import pyplot as plt
F = Matrix([[1.2,0.4],[0.4,1.2]])
coordinates=[[0,0],[0,1],[1,1],[1,0],[0,0]]
newcoordinates=[F*Matrix(coordinates[i]) for i in range(len(coordinates))]
bx =[Matrix(coordinates)[:,0], Matrix(coordinates)[:,1]]
bx2 = [[newcoordinates[i][0] for i in range(5)],[newcoordinates[i][1] for i in range(5)]]
Sigma = Matrix([[5,2],[2,3]])
N1 = Matrix([1,0])
N2 = Matrix([0,1])
Farea = F.det()*F.T.inv()
an1 = Farea*N1
an2 = Farea*N2
tn1 = Sigma.T*an1
tn2 = Sigma.T*an2
FirstPiola = Sigma.T*F.T.inv()*F.det()
SecondPiola = F.inv()*FirstPiola
TN1 = FirstPiola*N1
TN2 = FirstPiola*N2
STN1 = SecondPiola*N1
STN2 = SecondPiola*N2
Pt11 = F*N1+1/2*F*N2
Pt12 = Pt11+an1
Pt21 = 1/2*F*N1+F*N2
Pt22 = Pt21+an2
ar1 = Matrix([Pt11,Pt12]).reshape(2,2)
ar2 = Matrix([[Pt21],[Pt22]]).reshape(2,2)
A1dotted = Matrix([Pt11,Pt11+Matrix([1,0])]).reshape(2,2)
A2dotted = Matrix([Pt21,Pt21+Matrix([0,1])]).reshape(2,2)
A1 = Matrix([[1,0.5],[2,0.5]])
A2 = Matrix([[0.5,1],[0.5,2]])
artn1 = Matrix([Pt11,Pt11+tn1/10]).reshape(2,2)
artn2 = Matrix([Pt21,Pt21+tn2/10]).reshape(2,2)
arTN1 = Matrix([Matrix([1,0.5]),Matrix([1,0.5])+TN1/10]).reshape(2,2)
arTN2 = Matrix([Matrix([0.5,1]),Matrix([0.5,1])+TN2/10]).reshape(2,2)
arSTN1 = Matrix([Matrix([1,0.5]),Matrix([1,0.5])+STN1/10]).reshape(2,2)
arSTN2 = Matrix([Matrix([0.5,1]),Matrix([0.5,1])+STN2/10]).reshape(2,2)
fig, ax = plt.subplots(2, figsize=(6,8))
def plotArrow(p,M,t):
    x,y,dx,dy = M[0,0],M[0,1],float(M[1,0]-M[0,0]),float(M[1,1]-M[0,1])
    p.arrow(x,y,dx,dy,length_includes_head = True,head_width=.05, head_length=.05,alpha=t)
plotArrow(ax[0],A1,1)
plotArrow(ax[0],A2,1)
plotArrow(ax[0],arTN1,1)
plotArrow(ax[0],arTN2,1)
plotArrow(ax[0],arSTN1,.5)
plotArrow(ax[0],arSTN2,.5)
#rectangle coordinates
ax[0].plot(bx[0][:],bx[1][:])
ax[1].plot(bx2[0][:],bx2[1][:])
plotArrow(ax[1],ar1,1)
plotArrow(ax[1],ar2,1)
plotArrow(ax[1],artn1,1)
plotArrow(ax[1],artn2,1)
plotArrow(ax[1],A1dotted,.5)
plotArrow(ax[1],A2dotted,.5)
for i in ax:
    i.grid(True, which='both')
    i.axhline(y = 0, color = 'k',alpha = 0.5)
    i.axvline(x = 0, color = 'k',alpha = 0.5)
    i.set_xlabel("x")
    i.set_ylabel("y")

In the following tool, change the values of $F$ and $\sigma$ and watch how they affect the resulting deformation and forces acting on the different faces.