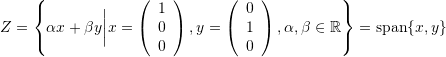Linear Vector Spaces: Examples and Problems
Example 1
Which of the following sets are orthonormal basis sets in the Euclidean vector space ![]() ?
?
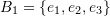 where
where 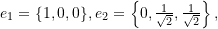 and
and 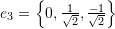
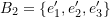 where
where 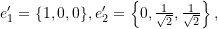 and
and 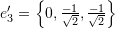
SOLUTION
For the set ![]() we have:
we have:
![]()
Therefore, ![]() ,
, ![]() , and
, and ![]() are unit vectors. In addition, we have:
are unit vectors. In addition, we have:
![]()
Therefore, the three vectors ![]() ,
, ![]() , and
, and ![]() are orthogonal to each other. Therefore,
are orthogonal to each other. Therefore, ![]() is an orthonormal basis set.
is an orthonormal basis set.
For the set ![]() we have:
we have:
![]()
Therefore, ![]() and
and ![]() are not orthogonal to each other. Therefore,
are not orthogonal to each other. Therefore, ![]() is not an orthonormal basis set. In fact, we have
is not an orthonormal basis set. In fact, we have ![]() which means that
which means that ![]() is linearly dependent, therefore, it is not even a basis set for
is linearly dependent, therefore, it is not even a basis set for ![]() . Notice that the symbol “.” is used in Mathematica for the dot product as shown below.
. Notice that the symbol “.” is used in Mathematica for the dot product as shown below.
View Mathematica Code
e2 = {0, 1/Sqrt[2], 1/Sqrt[2]};
e3 = {0, 1/Sqrt[2], -1/Sqrt[2]};
e1.e1
e1.e2
e1.e3
e2.e2
e2.e3
e3.e3
ep1 = {1, 0, 0};
ep2 = {0, 1/Sqrt[2], 1/Sqrt[2]};
ep3 = {0, -1/Sqrt[2], -1/Sqrt[2]};
ep1.ep1
ep1.ep2
ep1.ep3
ep2.ep2
ep2.ep3
ep3.ep3
View Numpy Python Code
import numpy as np
e1 = np.array([1, 0, 0]); # Matrix []
e2 = np.array([0, 1/np.sqrt(2), 1/np.sqrt(2)]);
e3 = np.array([0, 1/np.sqrt(2), -1/np.sqrt(2)]);
ep1 = np.array([1, 0, 0]);
ep2 = np.array([0, 1/np.sqrt(2), 1/np.sqrt(2)]);
ep3 = np.array([0, -1/np.sqrt(2), -1/np.sqrt(2)]);
print("B1 =",e1,e2,e3)
print("B2 =",ep1,ep2,ep3)
print("Check orthogonality")
print("e1.e1 =",np.dot(e1,e1)) # dot operation
print("e2.e2 =",np.dot(e2,e2))
print("e3.e3 =",np.dot(e3,e3))
print("e1.e2 =",np.dot(e1,e2))
print("e1.e3 =",np.dot(e1,e3))
print("e2.e3 =",np.dot(e2,e3))
print("e'1.e'1 =",np.dot(ep1,ep1))
print("e'2.e'2 =",np.dot(ep2,ep2))
print("e'3.e'3 =",np.dot(ep3,ep3))
print("e'1.e'2 =",np.dot(ep1,ep2))
print("e'1.e'3 =",np.dot(ep1,ep3))
print("e'2.e'3 =",np.dot(ep2,ep3))
View Sympy Python Code
import sympy as sp
sp.init_printing(use_latex="mathjax")
e1 = Matrix([1, 0, 0]); # Matrix []
e2 = Matrix([0, 1/sp.sqrt(2), 1/sp.sqrt(2)]);
e3 = Matrix([0, 1/sp.sqrt(2), -1/sp.sqrt(2)]);
ep1 = Matrix([1, 0, 0]);
ep2 = Matrix([0, 1/sp.sqrt(2), 1/sp.sqrt(2)]);
ep3 = Matrix([0, -1/sp.sqrt(2), -1/sp.sqrt(2)]);
display("B1=",e1,e2,e3)
display("B2=",ep1,ep2,ep3)
display("Check orthogonality")
display("e1.e1=",e1.dot(e1)) # dot operation
display("e2.e2=",e2.dot(e2))
display("e3.e3=",e3.dot(e3))
display("e1.e2=",e1.dot(e2))
display("e1.e3=",e1.dot(e3))
display("e2.e3=",e2.dot(e3))
display("e'1.e'1=",ep1.dot(ep1))
display("e'2.e'2=",ep2.dot(ep2))
display("e'3.e'3=",ep3.dot(ep3))
display("e'1.e'2=",ep1.dot(ep2))
display("e'1.e'3=",ep1.dot(ep3))
display("e'2.e'3=",ep2.dot(ep3))
Example 2
Find the angle between the two vectors ![]() , and
, and ![]() . Also use the cross product operation to find the vector
. Also use the cross product operation to find the vector ![]() .
.
SOLUTION
To find the geometric angle ![]() between the two vectors
between the two vectors ![]() and
and ![]() , we will use the dot product operation:
, we will use the dot product operation:
![]()
We have ![]() ,
, ![]() . Therefore,
. Therefore, ![]() and
and ![]() are orthogonal and
are orthogonal and ![]() .
.
The cross product between ![]() and
and ![]() gives the vector
gives the vector ![]() as follows:
as follows:
![]()
View Mathematica Code
y = {-1, 2, -1};
z = Cross[x, y]
Norm[x]
Norm[y]
thetaxy = ArcCos[x.y/Norm[x]/Norm[y]]
(*You can also find the angle between the two vectors using the command VectorAngle*)
VectorAngle[x,y]
View Numpy Python Code
from numpy.linalg import norm
x = np.array([1, 1, 1])
y = np.array([-1, 2, -1])
z = np.cross(x,y) # cross product
print("x =",x)
print("y =",y)
print("x\u00D7y =",z)
print("|x| =",norm(x)) #gives rounded value normalization
print("|y| =",norm(y))
# angle formula (a*b)/(norm a)(norm b)
print("\u03B8 =",np.arccos(np.dot(x,y)/norm(x)/norm(y)))
View Sympy Python Code
import sympy as sp
sp.init_printing(use_latex="mathjax")
x = Matrix([1, 1, 1])
y = Matrix([-1, 2, -1])
z = x.cross(y) # cross product
display("x=",x)
display("y=",y)
display("x\u00D7y=",z)
display("|x|=",x.norm()) # normalization
display("|y|=",y.norm())
# angle formula (a*b)/(norm a)(norm b)
display("\u03B8=",sp.acos(x.dot(y)/x.norm()/y.norm()))
Problems
- Show that the following sets are subspaces of
 . What is the graphical representation of each subspace? Find two different basis sets for each subspace.
. What is the graphical representation of each subspace? Find two different basis sets for each subspace.
- Show that the following sets are subspaces of
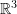 . What is the graphical representation of each subspace? Find two different basis sets for each subspace.
. What is the graphical representation of each subspace? Find two different basis sets for each subspace.
- Find three vectors that are orthogonal to
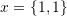 .
. - Find three vectors that are orthogonal to
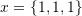 .
. - Choose a value for
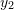 such that
such that 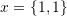 , and
, and 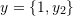 are linearly independent
are linearly independent - Choose two different sets of values for
 and
and 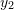 such that
such that 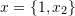 , and
, and 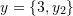 are linearly dependent.
are linearly dependent. - Verify that
 , and
, and  are linearly independent and then find the unique expansion of
are linearly independent and then find the unique expansion of 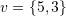 in the basis set
in the basis set 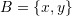 .
. - Verify that
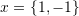 , and
, and  are linearly independent and then find the unique expansion of
are linearly independent and then find the unique expansion of 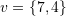 in the basis set
in the basis set 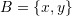 .
. - Find two different orthonormal basis sets and two different non-orthonormal basis sets for
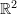 .
. - Find two different orthonormal basis sets and two different non-orthonormal basis sets for
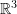 .
. - Find two different orthonormal basis sets and two different non-orthonormal basis sets for
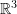 . The basis sets should include vector
. The basis sets should include vector 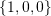 . Hint: An orthonormal basis set is a basis set whose vectors satisfy two conditions. The first condition is that the vectors in the basis set are orthogonal to each other and the second condition is that each vector has a unit norm.
. Hint: An orthonormal basis set is a basis set whose vectors satisfy two conditions. The first condition is that the vectors in the basis set are orthogonal to each other and the second condition is that each vector has a unit norm. - Show that the following vectors are linearly dependent
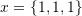 ,
, 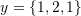 , and
, and  .
. - Show that the following vectors are linearly dependent
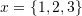 ,
, 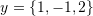 , and
, and 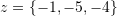 .
. - Verify that the following vectors are linearly independent
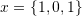 ,
, 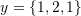 , and
, and 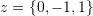 . Then, find the unique expansion of
. Then, find the unique expansion of  in the basis set
in the basis set 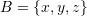 .
. - Verify that the following vectors are linearly independent
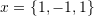 ,
, 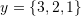 , and
, and 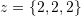 . Then, find the unique expansion of
. Then, find the unique expansion of 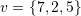 in the basis set
in the basis set 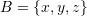 .
. - Use the cross product to find a vector orthogonal to both
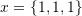 and
and  . Also, find the area of the parallelogram formed by the two vectors
. Also, find the area of the parallelogram formed by the two vectors  and
and 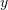 .
. - Use the cross product to find a vector orthogonal to both
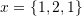 and
and 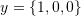 . Also, find the area of the parallelogram formed by the two vectors
. Also, find the area of the parallelogram formed by the two vectors  and
and 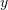 .
. - For the shown cuboid,
 ,
, 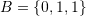 ,
, 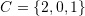 , and
, and 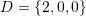 .
.

- Use the cross product operation to find two unit vectors orthogonal to the plane
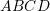 . What is the relationship between those two vectors?
. What is the relationship between those two vectors? - Use the cross product to find the area of the parallelogram
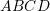 .
. - Find the angle between the vectors representing
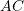 and
and 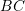 .
.
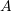 and ending at point
and ending at point 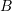 can be represented by a vector
can be represented by a vector 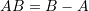 .
. - Use the cross product operation to find two unit vectors orthogonal to the plane
- Determine if the following vectors
 ,
, 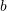 ,
,  , and d are linearly independent where
, and d are linearly independent where 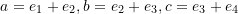 , and
, and 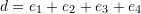 while
while 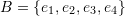 is a set of linearly independent vectors in
is a set of linearly independent vectors in 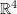 .
. - Which of the following functions
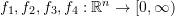 defined below satisfy the properties of a norm function (explain your answer).
defined below satisfy the properties of a norm function (explain your answer). 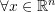 :
:
- Let
 . Assume that
. Assume that 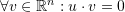 . Show that
. Show that  is the zero vector. (Hint: Show that the components of
is the zero vector. (Hint: Show that the components of  in an orthonormal basis set are all equal to zero)
in an orthonormal basis set are all equal to zero)