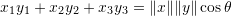Linear Vector Spaces: Additional Structure for Linear Vector Spaces
Learning Outcomes
- Calculate the norm of vectors, the dot product, and the distance between vectors
- Identify the relationship between the Mathematical definition and the associated geometry of linear vector spaces
Norm
Vector spaces can be endowed with a function called the “Norm” function. The norm function is used to describe the size of vectors in a linear vector space. It assigns strictly positive values for nonzero vectors.
Let ![]() be a linear vector space over
be a linear vector space over ![]() . A norm is defined as a function
. A norm is defined as a function ![]() that satisfies the following properties.
that satisfies the following properties. ![]() :
:
- Positive homogeneity or positive scalability:
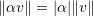
- Triangle inequality:
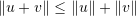
- Positive definiteness:
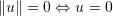
There are many candidate functions that satisfy the above definition. The “Euclidean Norm” is by far the most commonly used norm function. The Euclidean norm is defined as:
![]()
Exercises:
- Show that the triangle inequality is equivalent to:
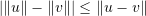
- Show that the Euclidean norm satisfies the properties of a norm function
- Show that the function
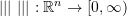 such that
such that  satisfies the properties of a norm function
satisfies the properties of a norm function
Metric (Distance)
Vector spaces can be endowed with a “Metric” function. The metric function is used to define a distance between any two vectors in a linear vector space. Let ![]() be a linear vector space over
be a linear vector space over ![]() . A metric is defined as a function
. A metric is defined as a function ![]() that satisfies the following properties.
that satisfies the following properties. ![]() :
:
- Symmetry:
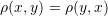
- Triangle inequality:
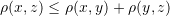
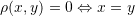
There are many candidate functions that satisfy the above definition. Usually, the metric function can be induced from the norm function by setting ![]() . The “Euclidean Metric” is a commonly used metric function and is generated by the “Euclidean Norm”:
. The “Euclidean Metric” is a commonly used metric function and is generated by the “Euclidean Norm”:
![]()
Exercises:
- Show that the Euclidean metric satisfies the properties of a metric function.
- Show that the function
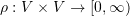 defined as:
defined as: 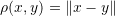 satisfies the properties of a metric function.
satisfies the properties of a metric function.
Inner Product
Vector spaces can be endowed with a function called the Inner Product function which associates each pair of vectors with a scalar quantity. The inner product function allows adding geometric structure to the vector space by defining orthogonality and angles. Let ![]() be an linear vector spaces over the field of complex numbers
be an linear vector spaces over the field of complex numbers ![]() . The inner product is a map
. The inner product is a map ![]() such that
such that ![]() :
:
- Conjugate symmetry:
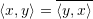
- Linearity in the first argument:
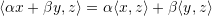
- Positive definiteness:
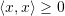 with
with 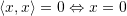
When ![]() is defined over the field of real numbers
is defined over the field of real numbers ![]() , the inner product becomes a bilinear map and conjugate symmetry becomes symmetry.
, the inner product becomes a bilinear map and conjugate symmetry becomes symmetry.
Euclidian Dot Product
The “Euclidean Dot Product” is one example of an inner product function. The dot product is defined ![]() as follows:
as follows:
![]()
The “Euclidean Dot Product” is related to the “Euclidean Norm” as follows, ![]() :
:
![]()
Euclidian Dot Product in  and
and 
In two and three dimensional vector spaces, the dot product is related to the geometric angle between two vectors as follows, ![]()
![]()
where ![]() is the geometric angle between the vectors x and y.
is the geometric angle between the vectors x and y.
Orthogonal Vectors
Two vectors are called “orthogonal” if their inner product is equal to zero. For Euclidean vector spaces, the term: “perpendicular” is used interchangeably with “orthogonal”.
Exercises:
- Show that