Engineering at Alberta Courses » Symmetric Tensors

Special Types of Linear Maps: Symmetric Tensors

Learning Outcomes

Identify the geometric function of a symmetric tensor.
Explain that a tensor from an n dimensional vector space to an n dimensional vector space is symmetric if and only if it possesses n real eigenvalues associated with n orthonormal eigenvectors.
Compute the process of diagonalization of a symmetric matrix. Recognize the geometric meaning of the process as being a simple change of basis using the eigenvectors of the symmetric matrix.
Identify that computing the invariants of the diagonalized form of a symmetric matrix is much simpler than computing them in a general form.

Symmetric Tensor Definition

Let $S:\mathbb{R}^n\rightarrow\mathbb{R}^n$ . $S$ is called a symmetric tensor if $S=S^T$ .
The following properties can be naturally deduced from the definition of symmetric tensors:

In component form, the matrix representation of 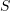$S$ is such that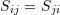 $S_{ij}=S_{ji}$
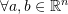$\forall a,b\in\mathbb{R}^n$ we have:

$Sa\cdot b=a\cdot Sb$
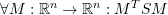$\forall M:\mathbb{R}^n\rightarrow\mathbb{R}^n:M^TSM$ is symmetric. In particular, if 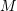$M$ is an orthogonal matrix associated with a coordinate transformation, then the matrix representation of 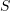$S$ stays symmetric in any coordinate system.

Symmetric Tensors Possess Real Eigenvalues and an Orthonormal Set of Eigenvectors

Symmetric tensors form a very important class of tensors that appear in many engineering applications. The following assertion leads to the simplification of the study of symmetric tensors.

ASSERTION:

A tensor $S:\mathbb{R}^n\rightarrow\mathbb{R}^n$ is symmetric if and only if it possesses $n$ real eigenvalues associated with $n$ orthonormal eigenvectors.

PROOF:

Let $\mathbb{C}$ be the space of complex numbers. First we will recall a few facts from complex analysis: If $a\in\mathbb{C}$ , then, $\exists a_1,a_2 \in \mathbb{R}$ such that $a=a_1+a_2i$ where $i^2=-1$ . The conjugate of $a$ , namely $\bar{a}$ is defined as $\bar{a}=a_1-a_2i$ . The product $a\bar{a}=a_1^2+a_2^2\in[0,\infty[$ . Additionally, $\forall a,b\in\mathbb{C},\overline{ab}=\bar{a}\bar{b}$ .

If $\lambda$ is an eigenvalue of $S$ , then, it is a solution to the $n^{th}$ degree polynomial equation $\det(S-\lambda I)=0$ . In general, this equation has $n$ solutions (roots) and some of these roots can be complex. We will now argue by contradiction: Assuming that $\lambda$ is a complex eigenvalue of $S$ , then $\exists p\neq 0, p\in\mathbb{C}^3$ such that:

$Sp=\lambda p$

Taking the conjugate of the above relation:

$S\bar{p}=\overline{\lambda p}=\bar{\lambda}\bar{p}$

If we then take the dot product of the first equation with $\bar{p}$ and the second equation with $p$ we get:

$\bar{p}\cdot Sp=\lambda \bar{p}\cdot p\hspace{10mm}p\cdot S\bar{p}=\bar{\lambda} p\cdot \bar{p}$

But, since $S$ is symmetric we have:

$\bar{p}\cdot Sp=p\cdot S\bar{p}\Rightarrow\lambda \bar{p}\cdot p-\bar{\lambda} p\cdot \bar{p}=(\lambda-\bar{\lambda}) p\cdot \bar{p}=0$

However, we have $\forall p \in\mathbb{C}^3,p\neq 0: \bar{p}\cdot p>0$ . Therefore, $\lambda=\bar{\lambda}$ and therefore, $\lambda \in \mathbb{R}$ .

The next step is to show that we can find a set of $n$ orthonormal eigenvectors associated with the $n$ real eigenvalues of $S$ . We first show this for any two distinct eigenvalues $\lambda_1\neq\lambda_2$ . Let $p_1$ and $p_2$ be the corresponding eigenvectors, then:

$p_1\cdot Sp_2=p_2\cdot Sp_1=\lambda_1(p_1\cdot p_2)=\lambda_2(p_1\cdot p_2)\Rightarrow(\lambda_1-\lambda_2)(p_1\cdot p_2)=0$

But since $\lambda_1\neq\lambda_2$ , then $p_1$ is orthogonal to $p_2$ .

Next, we assume that there is an eigenvalue $\lambda_1$ with multiplicity $m\geq2$ , i.e.,

(1) $\begin{equation*} \det(S-\lambda I)=(\lambda_1-\lambda)^m f(\lambda^{n-m}) \end{equation*}$

where $f$ is a real valued function. We need to show that there is a set of orthogonal (linearly independent) vectors $p_i, i\leq m$ associated with the eigenvalue $\lambda_1$ .
Let $p_1$ be an eigenvector associated with $\lambda_1$ . We can choose a set of vectors $y_i, 2\leq i\leq n$ that forms with $p_1$ an orthonormal basis set. Then, the following is the coordinate transformation matrix to change from the basis set $B=\{e_1,e_2,\cdots,e_n\}$ to $B'=\{p_1,y_2,y_3,\cdots,y_n\}$ :

$Q=\left( \begin{array}{cccc} p_{1,1}&p_{1,2}&\cdots&p_{1,n}\\ y_{2,1}&y_{2,2}&\cdots&y_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ y_{n,1}&y_{n,2}&\cdots&y_{n,n} \end{array} \right)$

If $S'$ is the matrix representation of $S$ in the coordinate system of $B'$ , then the components of $S'$ can be evaluated as follows:

$S'=QSQ^T= \left( \begin{array}{cccc} p_{1,1}&p_{1,2}&\cdots&p_{1,n}\\ y_{2,1}&y_{2,2}&\cdots&y_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ y_{n,1}&y_{n,2}&\cdots&y_{n,n} \end{array} \right) S \left( \begin{array}{cccc} p_{1,1}&y_{2,1}&\cdots&y_{n,1}\\ p_{1,2}&y_{2,2}&\cdots&y_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ p_{1,n}&y_{2,n}&\cdots&y_{n,n} \end{array} \right)$

Therefore:

$\begin{split} S'&=\left( \begin{array}{cccc} p_{1,1}&p_{1,2}&\cdots&p_{1,n}\\ y_{2,1}&y_{2,2}&\cdots&y_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\ y_{n,1}&y_{n,2}&\cdots&y_{n,n} \end{array} \right) \left( \begin{array}{cccc} \vdots&\vdots&\cdots&\vdots\\ Sp_1&Sy_2&\cdots&Sy_n\\ \vdots&\vdots&\cdots&\vdots\\ \end{array} \right)\\ & = \left( \begin{array}{cccc} p_1\cdot Sp_1&p_1\cdot Sy_2&\cdots&p_1\cdot Sy_n\\ y_2\cdot Sp_1&y_2\cdot Sy_2&\cdots&y_2\cdot Sy_n\\ \vdots&\vdots&\ddots&\vdots\\ y_n\cdot Sp_1&y_n\cdot Sy_2&\cdots&y_n\cdot Sy_n \end{array} \right) \end{split}$

Notice that $p_1\cdot Sp_1=\lambda_1$ and $\forall i:p_1\cdot Sy_i=Sp_1\cdot y_i=\lambda_1 (p_1\cdot y_i) = 0$ . Therefore:

$S'= \left( \begin{array}{cccc} \lambda_1&0&\cdots&0\\ 0&y_2\cdot Sy_2&\cdots&y_2\cdot Sy_n\\ \vdots&\vdots&\ddots&\vdots\\ 0&y_n\cdot Sy_2&\cdots&y_n\cdot Sy_n \end{array} \right)$

The above expression can be simplified if we consider the following matrix:

$Y=\left( \begin{array}{cccc} y_{2,1}&y_{2,2}&\cdots&y_{2,n}\\ y_{3,1}&y_{3,2}&\cdots&y_{3,n}\\ \vdots&\vdots&\ddots&\vdots\\ y_{n,1}&y_{n,2}&\cdots&y_{n,n} \end{array} \right)$

Then, $S'$ can be written in the following simplified form:

$S'= \left( \begin{array}{cc} \lambda_1&0\\ 0&YSY^T \end{array} \right)$

From the properties of the determinant, the characteristic equation of $S$ is:

$\det(S-\lambda I)=\det(S'-\lambda I)=(\lambda_1-\lambda)\det(YSY^T-\lambda I_{n-1})$

Where $I_{n-1}$ is the identity matrix defined on the subspace of the basis vectors $y_2, y_3,\cdots,y_n$ . It follows from (1) that $\lambda_1$ is an eigenvalue for the matrix $YSY^T$ , i.e., it is an eigenvalue of $S$ . Let $p_2$ be the corresponding eigenvector, then $p_2\in \text{span}\{y_2, y_3,\cdots,y_n\}$ . Therefore, $p_2\cdot p_1=0$ . Therefore, $\lambda_1$ has at least two perpendicular eigenvectors. By repeating the above argument, we can find $m$ orthogonal eigenvectors associated with $\lambda_1$ . Note that it is not possible to find more than $m$ orthogonal eigenvectors associated with $\lambda_1$ , otherwise this would lead to the contradictory conclusion that there are more than $n$ orthogonal eigenvectors in $\mathbb{R}^n$ .

Note that the choice of the eigenvectors is not necessarily unique since if $p$ is an eigenvector of $S$ , then so is $\alpha p$ for all nonzero real numbers $\alpha$ . In addition, if $p$ and $q$ are two orthogonal eigenvectors associated with an eigenvalue $\lambda_1$ , then there are infinite choices of sets of two orthonormal vectors associated with the eigenvalue $\lambda_1$ (why?).

It is now left to show that if $S$ has $n$ real eigenvalues associated with $n$ orthonormal eigenvectors, then $S$ is symmetric. Let $\{p_i\}_{i=1}^n$ be the set of $n$ orthonormal eigenvectors associated (respectively) with the the set of eigenvalues $\{\lambda_i\}_{i=1}^n$ , then $\forall x,y\in\mathbb{R}^n, x=\sum_{i=1}^n (x\cdot p_i) p_i$ and $y=\sum_{i=1}^n (y\cdot p_i) p_i$ . Therefore:

$x\cdot Sy=\left(\sum_{i=1}^n (x\cdot p_i) p_i\right)\cdot S\left(\sum_{j=1}^n (y\cdot p_j) p_j\right)=\sum_{i=1}^n \lambda_i(y\cdot p_i)(x\cdot p_i)$

Similarly:

$y\cdot Sx=\sum_{i=1}^n \lambda_i(y\cdot p_i)(x\cdot p_i)$

Therefore, $S$ is symmetric.

◼

Representation of Symmetric Tensors in 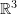$\mathbb{R}^3$

From the previous section, $S$ possesses three perpendicular eigenvectors, say $p, q$ and $r$ associated with the eigenvalues $\lambda_p, \lambda_q$ and $\lambda_r$ respectively. Assuming that $p, q$ and $r$ form a right handed orthonormal basis set in $\mathbb{R}^3$ then, $\forall a\in\mathbb{R}^3:a=(a\cdot p)p+(a\cdot q)q+(a\cdot r)r$ . Then:

$\begin{split} Sa&=(a\cdot p)Sp+(a\cdot q)Sq+(a\cdot r)Sr=\lambda_p(a\cdot p)p+\lambda_q(a\cdot q)q+\lambda_r(a\cdot r)r\\ &=\left(\lambda_p(p\otimes p)+\lambda_q(q\otimes q)+\lambda_r(r\otimes r)\right)a \end{split}$

Therefore, $S$ admits the representation:

(2) $\begin{equation*} S=\lambda_p(p\otimes p)+\lambda_q(q\otimes q)+\lambda_r(r\otimes r) \end{equation*}$

Note that this representation is not restricted to $\mathbb{R}^3$ but can be extended to any finite dimensional vector space $\mathbb{R}^n$ .

Diagonalization of Symmetric Matrices in 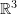$\mathbb{R}^3$

The representation of a symmetric tensor shown in (2) implies that if a coordinate system of the eigenvectors $p, q$ and $r$ is chosen, then $S$ admits a diagonal matrix representation.
This is easy to see when we consider a coordinate transformation from the basis set $B=\{e_1,e_2,e_3\}$ to the basis set $B'=\{p,q,r\}$ . The matrix of transformation has the form:

$Q=\left(\begin{array}{ccc} p_1 & p_2&p_3\\ q_1&q_2&q_3\\r_1&r_2&r_3\end{array}\right)$

If $S'$ is the representation of $S$ in the coordinate system described by $p, q$ and $r$ then:

$S'=QSQ^T=\left(\begin{array}{ccc} p_1 & p_2&p_3\\ q_1&q_2&q_3\\r_1&r_2&r_3\end{array}\right) \left(\begin{array}{ccc} S_{11} & S_{12}&S_{13}\\ S_{21} & S_{22}&S_{23}\\S_{31} & S_{32}&S_{33}\end{array}\right) \left(\begin{array}{ccc} p_1 & q_1&r_1\\ p_2&q_2&r_2\\p_3&q_3&r_3\end{array}\right)$

Utilizing the identities: $\sum_{j=1}^3S_{ij}p_j=\lambda_p p_i, \sum_{j=1}^3S_{ij}q_j=\lambda_q q_i$ and $\sum_{j=1}^3S_{ij}r_j=\lambda_r r_i$ :

$S'=\left(\begin{array}{ccc} p_1 & p_2&p_3\\ q_1&q_2&q_3\\r_1&r_2&r_3\end{array}\right) \left(\begin{array}{ccc} \lambda_p p_1 & \lambda_q q_1&\lambda_r r_1\\ \lambda_p p_2&\lambda_q q_2&\lambda_r r_2\\\lambda_p p_3&\lambda_q q_3&\lambda_r r_3\end{array}\right)$

Since $p\cdot p = \sum_{i=1}^3 p_i p_i=q\cdot q = \sum_{i=1}^3 q_i q_i=r\cdot r = \sum_{i=1}^3 r_i r_i=1$ and $p\cdot q=p\cdot r=q\cdot r=0$ then:

$S'=\left(\begin{array}{ccc} \lambda_p & 0&0\\ 0&\lambda_q&0\\0&0&\lambda_r\end{array}\right)$

Note that this representation is not restricted to $\mathbb{R}^3$ but can be extended to any finite dimensional vector space $\mathbb{R}^n$ .

Principal Invariants of a Symmetric Matrix in 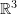$\mathbb{R}^3$

The diagonalization described in the previous section of a symmetric matrix allows expressing the three principal invariants of a symmetric matrix $S$ in terms of the three eigenvalues $\lambda_p, \lambda_q$ and $\lambda_r$ as follows:

$I_1(S) = \lambda_p+\lambda_q+\lambda_r$

$I_2(S) = \lambda_p\lambda_q+\lambda_p\lambda_r+\lambda_q\lambda_r$

$I_3(S) = \lambda_p\lambda_q\lambda_r$

Change the entries for the components of the symmetric matrix $S:\mathbb{R}^2\rightarrow\mathbb{R}^2$ and the tool will find the eigenvalues, eigenvectors and the new coordinate system in which $S$ is diagonal. The coordinate system used is illustrated with thick arrows:

Change the entries for the components of the symmetric matrix $S:\mathbb{R}^3\rightarrow\mathbb{R}^3$ and the tool will find the eigenvalues, eigenvectors and the new coordinate system in which $S$ is diagonal:

Geometric Representation of Symmetric Matrices

The geometric function of a symmetric matrix $S$ is to stretch an object along the principal direction (eigenvectors) of the matrix.

The following example illustrates the action of a symmetric matrix on the vectors forming a circle of radius 1 to transform the circle into an ellipse with major and minor radii equal to the eigenvalues of $S$ . The blue and red arrows show the eigenvectors of $S$ which upon transformation, do not change direction but change their length according to the corresponding eigenvalues. The black solid arrows show the vectors $e_1$ and $Se_1$ while the black dotted arrows show the vectors $e_2$ and $Se_2$ . Notice what happens to the orientation of the vectors when $\det(S)<0$ . Can you also find a combination of components producing $\det(S)=0$ ? What happens to the transformed circle?

Similarly, the following example illustrates the action of a symmetric tensor on the vectors forming a sphere of radius 1 to transform the sphere into an ellipsoid with radii equal to the eigenvalues of $S$ .

Positive Definite and Semi-Positive definite Symmetric Tensors

A symmetric tensor $S:\mathbb{R}^n\rightarrow\mathbb{R}^n$ is positive definite if $\forall a\in\mathbb{R}^n,a\neq 0:a\cdot Sa>0$ .
A symmetric tensor $S:\mathbb{R}^n\rightarrow\mathbb{R}^n$ is semi-positive definite if $\forall a\in\mathbb{R}^n:a\cdot Sa\geq 0$ .

ASSERTION:
Let $S:\mathbb{R}^n\rightarrow\mathbb{R}^n$ be symmetric, then $S$ is positive (semi-positive) definite if and only if $\forall \lambda$ in the set of eigenvalues of $S: \lambda>0 (\lambda\geq 0)$
PROOF:
Left as an exercise