Linear Maps Between Vector Spaces: Basic Definitions
Learning Outcomes
- Describe matrices as linear functions from one space to another. Describe the matrix as a representation of this function in a particular ONB.
- Calculate the Kernel of simple matrices. Describe what the Kernel represents. Define an invertible matrix as one that has one element in the kernel.
- Calculate the components of a matrix in various ONBs
- Compute matrix multiplication
- Differentiate between an invertible (bijective) matrix and one that is a non-invertible matrix using the geometry of a linear map.
- Calculate the determinant of a 2×2 and a 3×3 matrix. Explain that the determinant is a measure of whether a matrix is invertible or not.
- Identify and apply the properties of the determinant function.
- Define eigenvalues and eigenvectors. Identify the properties of the eigenvalues and eigenvectors.
- Eigenvalues and Eigenvectors: Visualize the geometry of eigenvalues and eigenvectors (The online tool helps the visualization of the eigenvector as the vector that does not change direction when transformed by the matrix).
Compute eigenvalues and eigenvectors.
Linear Maps
A linear map ![]() between two vectors spaces
between two vectors spaces ![]() and
and ![]() is a function
is a function ![]() such that
such that ![]() :
:
![]()
Notice that the addition of two linear maps and their multiplication by scalars produce a linear map as well, which imply that the set of linear maps is also a linear vector space.
It is important not to confuse linear maps with affine maps. For example, the function ![]() defined such that
defined such that ![]() is not a linear map but rather an affine map.
is not a linear map but rather an affine map. ![]() is not a linear map since in general
is not a linear map since in general ![]() . On the other hand, the function
. On the other hand, the function ![]() defined such that
defined such that ![]() is indeed a linear map.
is indeed a linear map.
Tensors
Linear maps between finite dimensional linear vector spaces is one example of functions that are referred to as Tensors. Tensor analysis provides a natural and concise mathematical tool for the analysis of various engineering problems, in particular, solid mechanics. For a detailed description of tensors, refer to the Wolfram article on tensors.
According to wikipedia, the origin of the word “Tensors” dates back to the nineteenth century when it was introduced by Woldemar Voigt. It is likely that the word originated because one of the early linear operators introduced was the symmetric Cauchy stress matrix which functions to convert area vectors to force vectors. At the time, perhaps the scientists were interested in things that “stretch” and thus, the word “Tensor” from the Latin route “Tendere” came about.
Kernel of Linear Maps
Let T be a linear map between two vector spaces ![]() and
and ![]() . Then, the kernel of
. Then, the kernel of ![]() or
or ![]() is the set of all vectors that are mapped into the zero vector, i.e.:
is the set of all vectors that are mapped into the zero vector, i.e.:
![]()
For example, consider the linear map ![]() defined such that
defined such that ![]() ,
, ![]() . Then, the kernel of this linear map consists of al the vectors in
. Then, the kernel of this linear map consists of al the vectors in ![]() that are mapped to zero, i.e., the vectors whose components
that are mapped to zero, i.e., the vectors whose components ![]() and
and ![]() satisfy:
satisfy:
![]()
There are infinitely many vectors that satisfy this condition. The set of all those vectors is given as:
Matrix Representation of Linear Maps
The matrix representation of linear maps is the most convenient way to represent linear maps when orthonormal basis sets are chosen for the underlying vector spaces. Consider the linear map ![]() . Let
. Let ![]() and
and ![]() be the orthonormal basis sets for
be the orthonormal basis sets for ![]() and
and ![]() respectively. Then, because of the linearity of the map, the map is indeed well defined by the components of the vectors
respectively. Then, because of the linearity of the map, the map is indeed well defined by the components of the vectors ![]() . Since
. Since ![]() we can assume that it has
we can assume that it has ![]() components which can be denoted as follows:
components which can be denoted as follows:
![]()
![]()
![Rendered by QuickLaTeX.com \[ Tx= \left( \begin{array}{cccc} T_{11}&T_{12}&\cdots&T_{1n}\\ T_{21}&T_{22}&\cdots&T_{2n}\\ \vdots & \vdots &\ddots &\vdots\\ T_{m1}&T_{m2}&\cdots &T_{mn} \end{array} \right) \left( \begin{array}{cc} x_1\\ x_2\\ \vdots\\ \vdots\\ x_n \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-7120c2a55ed8a9643dc31fab730debca_l3.png)
Matrix Representation and Change of Basis
The components of the matrix representation of ![]() defined above depend on the choice of the orthonormal basis sets for each vector space. For the discussion in this section, we will restrict ourselves to square matrices, i.e., linear maps between vector spaces of the same dimension.
defined above depend on the choice of the orthonormal basis sets for each vector space. For the discussion in this section, we will restrict ourselves to square matrices, i.e., linear maps between vector spaces of the same dimension.
Let ![]() . Let
. Let ![]() be the chosen orthonormal basis set for both vector spaces and let
be the chosen orthonormal basis set for both vector spaces and let ![]() be another orthonormal basis set and let
be another orthonormal basis set and let ![]() be the matrix of coordinate transformation as defined in the Change of Basis section. The matrix representation of
be the matrix of coordinate transformation as defined in the Change of Basis section. The matrix representation of ![]() when
when ![]() is chosen as the basis set is denoted by
is chosen as the basis set is denoted by ![]() . The relationship between
. The relationship between ![]() and
and ![]() can be obtained as follows:
can be obtained as follows:
Let ![]() , denote
, denote ![]() . Let
. Let ![]() and
and ![]() denote the representation of
denote the representation of ![]() and
and ![]() when
when ![]() is chosen as the coordinate system. Therefore in each coordinate system we have:
is chosen as the coordinate system. Therefore in each coordinate system we have:
![]()
![]()
![]()
This is true for every ![]() , therefore:
, therefore:
![]()
In the following tool, you can choose the components of the matrix ![]() and the vector
and the vector ![]() along with an angle
along with an angle ![]() of the counterclockwise rotation of the coordinate system. The tool then applies the transformation of coordinates from the coordinate system
of the counterclockwise rotation of the coordinate system. The tool then applies the transformation of coordinates from the coordinate system ![]() , to
, to ![]() where
where ![]() are vectors rotated by
are vectors rotated by ![]() counterclockwise from
counterclockwise from ![]() , and
, and ![]() . On the left hand side, the tool draws the vector
. On the left hand side, the tool draws the vector ![]() in blue, the vector
in blue, the vector ![]() in red, the original coordinate system in black, and the vectors of the new coordinate system in dashed black. At the bottom of the left hand side drawing you will find the expressions for
in red, the original coordinate system in black, and the vectors of the new coordinate system in dashed black. At the bottom of the left hand side drawing you will find the expressions for ![]() and
and ![]() using the basis set
using the basis set ![]() . On the right hand side, the tool draws the vectors
. On the right hand side, the tool draws the vectors ![]() in blue,
in blue, ![]() in red, and the new coordinate system in black. At the bottom of the right hand side, you will find the expressions for
in red, and the new coordinate system in black. At the bottom of the right hand side, you will find the expressions for ![]() and
and ![]() using the basis set
using the basis set ![]() . You can also check out the external tool built in MecsimCalc for changes of basis.
. You can also check out the external tool built in MecsimCalc for changes of basis.
Similarly, the following tool is for three dimensional Euclidean vector spaces. The new coordinate system ![]() is obtained by simultaneously applying a counterclockwise rotation
is obtained by simultaneously applying a counterclockwise rotation ![]() , and
, and ![]() around the first, second, and third coordinate system axis, respectively. The view can be zoomed, rotated or panned by the mouse scroll wheel, holding down the left mouse button and moving the mouse, and holding down the right mouse button and moving the mouse.
around the first, second, and third coordinate system axis, respectively. The view can be zoomed, rotated or panned by the mouse scroll wheel, holding down the left mouse button and moving the mouse, and holding down the right mouse button and moving the mouse.
Tensor Product
Let ![]() and
and ![]() . The tensor product denoted by
. The tensor product denoted by ![]() is a linear map
is a linear map ![]() defined such that
defined such that ![]() :
:
![]()
In simple words, the tensor product defined above utilizes the linear dot product operation and a fixed vector ![]() to produce a real number using the expression
to produce a real number using the expression ![]() , which is conveniently a linear function of
, which is conveniently a linear function of ![]() . The resulting number is then multiplied by the vector
. The resulting number is then multiplied by the vector ![]() .
.
Obviously, the tensor product of vectors belonging to vector spaces of dimensions higher than 1 are not invertible, in fact, the range of ![]() is one dimensional (why?)!
is one dimensional (why?)!
The following are some of the properties of the tensor product that can be deduced directly from the definition and the properties of the dot product operation, ![]() :
:
![]()
![]()
![]()
![]()
![]()
Matrix Representation of the Tensor Product
Let ![]() and consider the tensor product
and consider the tensor product ![]() . Consider the orthonormal basis set
. Consider the orthonormal basis set ![]() . Then, the tensor product can be expressed in component form as follows:
. Then, the tensor product can be expressed in component form as follows:
![Rendered by QuickLaTeX.com \[ v\otimes u=(v_1e_1+v_2e_2+v_3e_3)\otimes (u_1e_1+u_2e_2+u_3e_3)=\sum_{i,j=1}^3 v_iu_j (e_i\otimes e_j) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-21ed9ae8ec3be3788ef9e537ceab5a03_l3.png)
Now, ![]() we have:
we have:
![]()
Which, can be represented in matrix form as follows:
![Rendered by QuickLaTeX.com \[ (v\otimes u)x= \left( \begin{array}{cc} \sum_{j=1}^3 v_1u_j x_j\\ \sum_{j=1}^3 v_2u_j x_j\\ \sum_{j=1}^3 v_3u_j x_j \end{array} \right)= \left( \begin{array}{ccc} v_1u_1&v_1u_2&v_1u_3\\ v_2u_1&v_2u_2&v_2u_3\\ v_3u_1&v_3u_2&v_3u_3 \end{array} \right) \left( \begin{array}{cc} x_1\\ x_2\\ x_3 \end{array} \right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a474fcd7f93606af4345151256c6e7bc_l3.png)
Tensor Product Representation of Linear Maps
A linear map can be decomposed into the sum of multiple tensor products. For example, one can think of a linear map ![]() between three dimensional vector spaces, as the sum of three tensor products:
between three dimensional vector spaces, as the sum of three tensor products:
![]()
There is a direct relationship between the tensor product representation and the matrix representation as follows: let ![]() and let
and let ![]() be an orthonormal basis set for both vector spaces, then,
be an orthonormal basis set for both vector spaces, then, ![]() :
:
![Rendered by QuickLaTeX.com \[ Tx=T\sum_{j=1}^3(x_je_j)=\sum_{j=1}^3(x_jTe_j)=\sum_{i=1}^3 \sum_{j=1}^3 T_{ij}x_j e_i=\sum_{i=1}^3 \sum_{j=1}^3 T_{ij}(x\cdot e_j) e_i=\sum_{i=1}^3 \sum_{j=1}^3 T_{ij}(e_i\otimes e_j) x \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-44ea5b97dec7a3ea4e34fbf55217851e_l3.png)
![]()
Video
See “Tensor Product” Video here
The Set of Linear Maps
In these pages, the notation ![]() is used to denote the set of linear maps between
is used to denote the set of linear maps between ![]() and
and ![]() . i.e.,:
. i.e.,:
![]()
![]()
The Algebraic Structure of The Set of Linear Maps
In addition to being a vector space, the elements of the sets of linear maps has an algebraic structure arising naturally from the composition operation. Let ![]() and
and ![]() , then, the composition map
, then, the composition map ![]() is also a linear map since
is also a linear map since![]() ,
,![]() :
:
![Rendered by QuickLaTeX.com \[ \begin{split} T(\alpha x + \beta y)&=V\circ U(\alpha x + \beta y)\\ &=V(U((\alpha x + \beta y)))\\ &=V(\alpha U(x)+\beta U(y))\\ &=\alpha V(U(x)) + \beta V(U(y))\\ &=\alpha T(x) + \beta T(y) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-fa6e30c19d4f56094f12dae56fe567e8_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{split} Lx&=\left( \begin{array}{c} \sum_{j=1}^nL_{1j}x_j\\ \sum_{j=1}^nL_{2j}x_j\\ \cdots\\ \sum_{j=1}^nL_{lj}x_j \end{array} \right)\\ NMx&=N\left( \begin{array}{c} \sum_{j=1}^nM_{1j}x_j\\ \sum_{j=1}^nM_{2j}x_j\\ \cdots\\ \sum_{j=1}^nM_{mj}x_j \end{array}\right) = \left( \begin{array}{c} \sum_{k=1}^m\sum_{j=1}^nN_{1k}M_{kj}x_j\\ \sum_{k=1}^m\sum_{j=1}^nN_{1k}M_{kj}x_j\\ \cdots\\ \sum_{k=1}^m\sum_{j=1}^nN_{lk}M_{kj}x_j \end{array} \right) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-c97ddeeee5d2af5d5040c826de3c4ff4_l3.png)
![]()
However, if ![]() , and their respective associated matrices are
, and their respective associated matrices are ![]() then both composition maps are well defined. The first one is the composition map
then both composition maps are well defined. The first one is the composition map ![]() with its associated matrix
with its associated matrix ![]() while the second is the composition map
while the second is the composition map ![]() and its associated matrix
and its associated matrix ![]() . In general, these two maps are not identical.
. In general, these two maps are not identical.
The identity map ![]() and its associated identity matrix
and its associated identity matrix ![]() is the identity element in the algebraic structure of
is the identity element in the algebraic structure of ![]()
Bijective(Invertible) Linear Maps
In this section, we are concerned with the linear maps represented by square matrices ![]() and whether these linear maps (linear functions) are invertible or not. Recall from the Mathematical Preliminaries section that a function
and whether these linear maps (linear functions) are invertible or not. Recall from the Mathematical Preliminaries section that a function ![]() is invertible if
is invertible if ![]() such that
such that ![]() .
. ![]() is denoted by
is denoted by ![]() . Let’s now consider the linear map (represented by a matrix
. Let’s now consider the linear map (represented by a matrix ![]() )
) ![]() , what are the conditions that guarantee the existence of
, what are the conditions that guarantee the existence of ![]() such that
such that ![]() where
where ![]() is the identity matrix? We will answer this question using a few statements:
is the identity matrix? We will answer this question using a few statements:
Statement 1: Let ![]() be a linear map. Then
be a linear map. Then ![]() .
This statement is simple to prove. First note that since
.
This statement is simple to prove. First note that since ![]() is a linear map, then
is a linear map, then ![]() .
First, assume
.
First, assume ![]() is injective. Since
is injective. Since ![]() and since
and since ![]() is injective therefore, 0 is the unique image of 0. Therefore,
is injective therefore, 0 is the unique image of 0. Therefore, ![]() . For the opposite statement, assume that
. For the opposite statement, assume that ![]() . We will argue by contradiction, i.e., assuming that
. We will argue by contradiction, i.e., assuming that ![]() is not injective. Therefore,
is not injective. Therefore, ![]() with
with ![]() but
but ![]() . Since
. Since ![]() is linear we have
is linear we have ![]() . Therefore,
. Therefore, ![]() which is a contradiction. Therefore
which is a contradiction. Therefore ![]() is injective.
is injective.
◼
Statement 2: Let ![]() be a linear map. Then
be a linear map. Then ![]() .
First assume that
.
First assume that ![]() is invertible, therefore,
is invertible, therefore, ![]() is injective. Statement 1 asserts then that
is injective. Statement 1 asserts then that ![]() .
Assume now that
.
Assume now that ![]() . Therefore, from statement 1,
. Therefore, from statement 1, ![]() is injective. We need to show that
is injective. We need to show that ![]() is surjective. Note that using Statement 1, and since an invertible map is also injective, then we just need to show that
is surjective. Note that using Statement 1, and since an invertible map is also injective, then we just need to show that ![]() . This can be proven by picking a basis set
. This can be proven by picking a basis set ![]() for
for ![]() and showing that the set
and showing that the set ![]() is linearly independent which right away implies that
is linearly independent which right away implies that ![]() is surjective. Since
is surjective. Since ![]() is injective and
is injective and ![]() is linearly independent we have:
is linearly independent we have:
![]()
![]()
![]()
◼
Statement 3: Let ![]() be a linear map. Then
be a linear map. Then ![]() the
the ![]() vectors forming the square matrix of
vectors forming the square matrix of ![]() are linearly independent.
are linearly independent.
First assume that ![]() are
are ![]() linearly independent vectors that form the row vectors of the linear map
linearly independent vectors that form the row vectors of the linear map ![]() . We will argue by contradiction. Assume that
. We will argue by contradiction. Assume that ![]() and
and ![]() . Then,
. Then, ![]() . However, since
. However, since ![]() are linearly independent, they form a basis set and
are linearly independent, they form a basis set and ![]() can be expressed in terms of all of them. Therefore
can be expressed in terms of all of them. Therefore ![]() . But
. But ![]() is orthogonal to all of them, then
is orthogonal to all of them, then ![]() . Therefore,
. Therefore, ![]() and the map is bijective using statement 2.
For the opposite direction, assume that the map is bijective yet
and the map is bijective using statement 2.
For the opposite direction, assume that the map is bijective yet ![]() are linearly dependent. Since they are linearly dependent, therefore there is at least one vector that can be represented as a linear combination of the other vectors. Without loss of generality, assume that
are linearly dependent. Since they are linearly dependent, therefore there is at least one vector that can be represented as a linear combination of the other vectors. Without loss of generality, assume that ![]() . Therefore
. Therefore
![Rendered by QuickLaTeX.com \[\begin{split} \forall x\in\mathbb{R}^n:Tx&=\sum_{i=1}^n (v_i\cdot x)e_i=\sum_{i=1}^{n-1}\left((v_i\cdot x)e_i\right)+\left(\left(\sum_{i=1}^{n-1}\alpha_iv_i\right)\cdot x\right)e_n\\ & =\sum_{i=1}^{n-1}(v_i\cdot x)(e_i+\alpha_ie_n) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-13eb2bd8776d96e19c18ae4d3f999472_l3.png)
◼
Statement 3 asserts that a square matrix is invertible if and only if the rows are linearly independent. In the following section, we will present the determinant of a matrix as a measure of whether the rows are linearly independent or not.
Determinant
The determinant of a matrix representation of a linear map is a real valued function of the components of a square matrix. The determinant is used to indicate whether the rows of the matrix ![]() are linearly dependent or not. If they are, then the determinant is equal to zero, otherwise, the determinant is not equal to zero. In the following, we will show the definition of the determinant function for
are linearly dependent or not. If they are, then the determinant is equal to zero, otherwise, the determinant is not equal to zero. In the following, we will show the definition of the determinant function for ![]() and for a general
and for a general ![]() . We will also verify that the determinant of
. We will also verify that the determinant of ![]() is equal to zero if and only if the row vectors of the matrix are linearly dependent for the cases
is equal to zero if and only if the row vectors of the matrix are linearly dependent for the cases ![]() and
and ![]() .
.
DETERMINANT OF 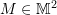 :
:
Let ![]() such that
such that
![]()
The determinant of ![]() is defined as:
is defined as:
![]()
Clearly, the vectors ![]() and
and ![]() are linearly dependent if and only if
are linearly dependent if and only if ![]() . The determinant of the matrix
. The determinant of the matrix ![]() has a geometric meaning (See Figure 1). Consider the two unit vectors
has a geometric meaning (See Figure 1). Consider the two unit vectors ![]() and
and ![]() . Let
. Let ![]() and
and ![]() . The area of the parallelogram formed by
. The area of the parallelogram formed by ![]() and
and ![]() is equal to the determinant of the matrix
is equal to the determinant of the matrix ![]() .
.
The following is true ![]() and
and ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{split} \det{(NM)} & =\det{N}\det{M}\\ \det{\alpha M}& =\alpha^2\det{M}\\ \det{I} & = 1 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-a5613454fceb3f0de7c24e15491488bc_l3.png)
where ![]() is the identity matrix.
is the identity matrix.
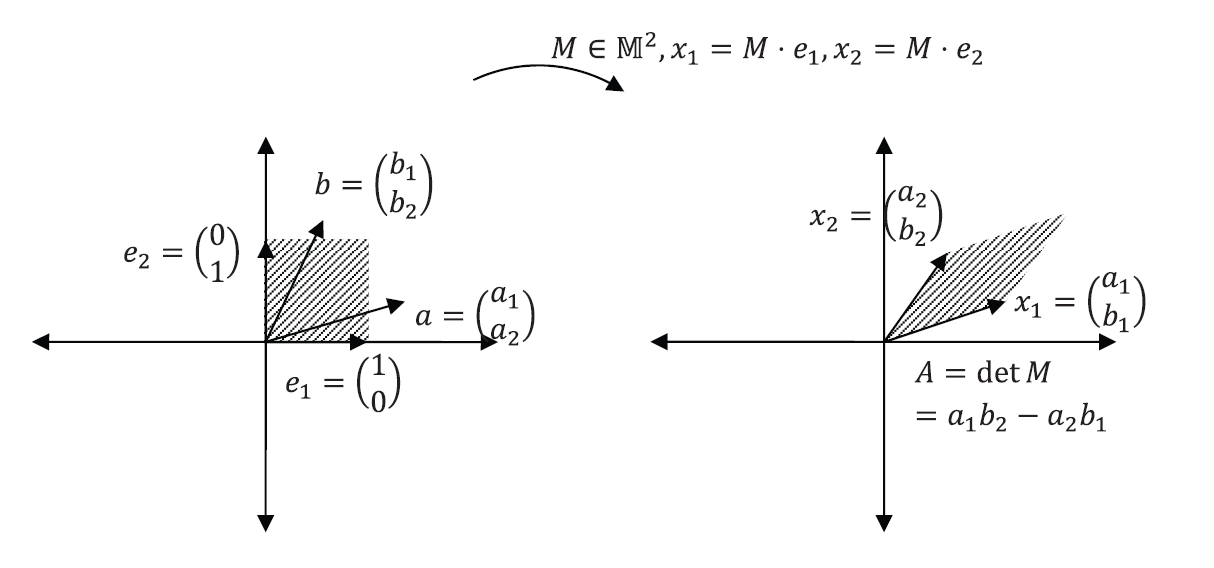
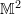
DETERMINANT OF 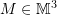 :
:
Let ![]() such that
such that
![Rendered by QuickLaTeX.com \[ M=\left(\begin{matrix}a_1 & a_2 & a_3\\b_1& b_2& b_3\\c_1&c_2&c_3\end{matrix}\right) \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-4c2c270bf5cbca0ed8632a823160259d_l3.png)
If ![]() , and
, and ![]() , then the determinant of
, then the determinant of ![]() is defined as:
is defined as:
![]()
I.e., ![]() the tripe product of
the tripe product of ![]() , and
, and ![]() . From the results of the triple product, the vectors
. From the results of the triple product, the vectors ![]() , and
, and ![]() are linearly dependent if and only if
are linearly dependent if and only if ![]() . The determinant of the matrix M has a geometric meaning (See Figure 2). Consider the three unit vectors
. The determinant of the matrix M has a geometric meaning (See Figure 2). Consider the three unit vectors ![]() , and
, and ![]() . Let
. Let ![]() , and
, and ![]() . The determinant of
. The determinant of ![]() is also equal to the triple product of
is also equal to the triple product of ![]() , and
, and ![]() and gives the volume of the parallelepiped formed by
and gives the volume of the parallelepiped formed by ![]() , and
, and ![]() .
.
![Rendered by QuickLaTeX.com \[\begin{split} \det{M}&=a\cdot(b\times c)=a_1(b_2c_3-b_3c_2)+a_2(b_3c_1-b_1c_3)+a_3(b_1c_2-b_2c_1)\\ &=a_1(b_2c_3-b_3c_2)+b_1(a_3c_2-a_2c_3)+c_1(a_2b_3-b_2a_3)\\ &=x_1\cdot (x_2\times x_3)\\ &=Me_1\cdot (Me_2\times Me_3) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-d54db71ce4c372dd403eb18b02fdd2e9_l3.png)
Additionally, ![]() and
and ![]() are linearly independent, it is straightforward to show the following:
are linearly independent, it is straightforward to show the following:
![]()
In other words, the determinant gives the ratio between ![]() and
and ![]() where
where ![]() is the volume of the transformed parallelepiped between
is the volume of the transformed parallelepiped between ![]() , and
, and ![]() and
and ![]() is the volume of the parallelepiped between
is the volume of the parallelepiped between ![]() , and
, and ![]() .
The alternator
.
The alternator ![]() defined in Mathematical Preliminaries can be used to write the followign useful equality:
defined in Mathematical Preliminaries can be used to write the followign useful equality:
![]()
The following is true ![]() and
and ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{split} \det{(NM)} & =\det{N}\det{M}\\ \det{\alpha M}& =\alpha^3\det{M}\\ \det{I} & = 1 \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-bc7c79cf72ab376ba7ccf41d74cd46db_l3.png)
where ![]() is the identity matrix.
is the identity matrix.
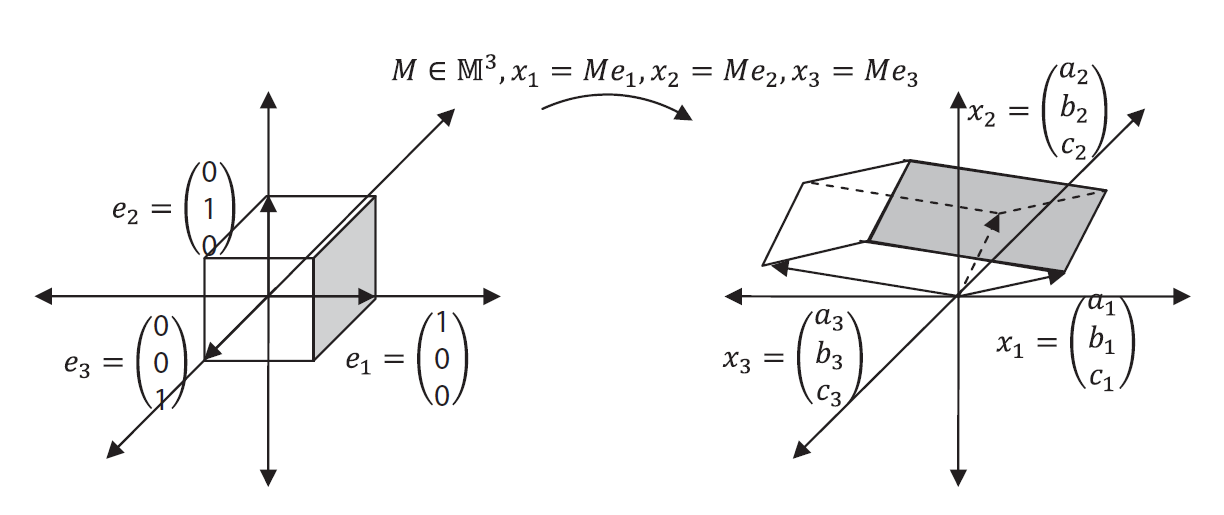

AREA TRANSFORMATION IN  :
:
The following is a very important formula (often referred to as “Nanson’s Formula”) that relates the cross product of vectors in ![]() to the cross product of their images under a linear transformation. This formula is used to relate area vectors before mapping to area vectors after mapping.
to the cross product of their images under a linear transformation. This formula is used to relate area vectors before mapping to area vectors after mapping.
ASSERTION:
Let ![]() . Let
. Let ![]() be an invertible matrix. Show the following relationship:
be an invertible matrix. Show the following relationship:
![]()
PROOF:
Let ![]() be an arbitrary vector in
be an arbitrary vector in ![]() . From the relationships above we have:
. From the relationships above we have:
![]()
Therefore:
![]()
Therefore:
![]()
Nanson’s formula is sometimes written as follows:
![]()
where
![Rendered by QuickLaTeX.com \[\begin{split} A&=\|u\times v\|\\ N&=\frac{1}{A}(u\times v)\\ a&=\|Mu\times Mv\|\\ n&=\frac{1}{a}(Mu\times Mv) \end{split} \]](https://engcourses-uofa.ca/wp-content/ql-cache/quicklatex.com-bad3133d928efed838a55b6f4b0b61ac_l3.png)
DETERMINANT OF  :
:
The determinant of ![]() is defined using the recursive relationship:
is defined using the recursive relationship:
![]()
where ![]() and is formed by eliminating the 1st row and
and is formed by eliminating the 1st row and ![]() column of the matrix
column of the matrix ![]() . It can be shown that
. It can be shown that ![]() the rows of
the rows of ![]() are linearly dependent.
are linearly dependent.
Video
See “Area Transformation” Video here
Eigenvalues and Eigenvectors
Let ![]() is called an eigenvalue of the tensor
is called an eigenvalue of the tensor ![]() if
if ![]() such that
such that ![]() . In this case,
. In this case, ![]() is called an eigenvector of
is called an eigenvector of ![]() associated with the eigenvalue
associated with the eigenvalue ![]() .
.
Similar Matrices
Let ![]() . Let
. Let ![]() be an invertible tensor. The matrix representations of the tensors
be an invertible tensor. The matrix representations of the tensors ![]() and
and ![]() are termed “similar matrices”.
are termed “similar matrices”.
Similar matrices have the same eigenvalues while their eigenvectors differ by a linear transformation as follows: If ![]() is an eigenvalue of
is an eigenvalue of ![]() with the associated eigenvector
with the associated eigenvector ![]() then:
then:
![]()
Therefore, ![]() is an eigenvalue of
is an eigenvalue of ![]() and
and ![]() is the associated eigenvector. Similarly, if
is the associated eigenvector. Similarly, if ![]() is an eigenvalue of
is an eigenvalue of ![]() with the associated eigenvector
with the associated eigenvector ![]() then:
then:
![]()
Therefore, ![]() is an eigenvalue of
is an eigenvalue of ![]() and
and ![]() is the associated eigenvector. Therefore, similar matrices share the same eigenvalues.
is the associated eigenvector. Therefore, similar matrices share the same eigenvalues.
The Eigenvalues and Eigenvector Problem
Given a tensor ![]() , we seek a nonzero vector
, we seek a nonzero vector ![]() and a real number
and a real number ![]() such that:
such that: ![]() . This is equivalent to
. This is equivalent to ![]() . In other words, the eigenvalue is a real number that makes the tensor
. In other words, the eigenvalue is a real number that makes the tensor ![]() not invertible while the eigenvector is a non-zero vector
not invertible while the eigenvector is a non-zero vector ![]() . Considering the matrix representation of the tensor
. Considering the matrix representation of the tensor ![]() , the eigenvalue is the solution to the following equation:
, the eigenvalue is the solution to the following equation:
![]()
The above equation is called the characteristic equation of the matrix ![]() .
.
From the properties of the determinant function, the characteristic equation is an ![]() degree polynomial of the unknown
degree polynomial of the unknown ![]() where
where ![]() is the dimension of the underlying space.
is the dimension of the underlying space.
In particular, ![]() , where
, where ![]() are called the polynomial coefficients. Thus, the solution to the characteristic equation abides by the following facts from polynomial functions:
are called the polynomial coefficients. Thus, the solution to the characteristic equation abides by the following facts from polynomial functions:
– Polynomial roots: A polynomial ![]() has a root
has a root ![]() if
if ![]() divides
divides ![]() , i.e.,
, i.e., ![]() such that
such that ![]() .
.
– The fundamental theorem of Algebra states that a polynomial of degree ![]() has
has ![]() complex roots that are not necessarily distinct.
complex roots that are not necessarily distinct.
– The Complex Conjugate Root Theorem states that If ![]() is a complex root of a polynomial with real coefficients, then the conjugate
is a complex root of a polynomial with real coefficients, then the conjugate ![]() is also a complex root.
is also a complex root.
Therefore, the eigenvalues can either be real or complex numbers. If one eigenvalue is a real number, then there exists a vector with real valued components that is an eigenvector of the tensor. Otherwise, the only eigenvectors are complex eigenvectors which are elements of finite dimensional linear spaces over the field of complex numbers.
Graphical Representation of the Eigenvalues and Eigenvectors
The eigenvectors of a tensor ![]() are those vectors that do not change their direction upon transformation with the tensor
are those vectors that do not change their direction upon transformation with the tensor ![]() but their length is rather magnified or reduced by a factor
but their length is rather magnified or reduced by a factor ![]() . Notice that an eigenvalue can be negative (i.e., the transformed vector can have an opposite direction). Additionally, an eigenvalue can have the value of 0. In that case, the eigenvector is an element of the kernel of the tensor.
. Notice that an eigenvalue can be negative (i.e., the transformed vector can have an opposite direction). Additionally, an eigenvalue can have the value of 0. In that case, the eigenvector is an element of the kernel of the tensor.
The following example illustrates this concept. Choose four entries for the matrix ![]() and press evaluate.
The tool then draws 8 coloured vectors across the circle and their respective images across the ellipse. Use visual inspection to identify which vectors keep their original direction.
and press evaluate.
The tool then draws 8 coloured vectors across the circle and their respective images across the ellipse. Use visual inspection to identify which vectors keep their original direction.
The tool also finds at most two eigenvectors (if they exist) and draws them in black along with their opposite directions. A similar tool is available on the external MecsimCalc python app builder. Use the tool to investigate the eigenvalues and eigenvectors of the following matrices:
![]()
After inspection, you should have noticed that every vector is an eigenvector for the identity matrix ![]() since
since ![]() , i.e.,
, i.e., ![]() possesses one eigenvalue which is 1 but all the vectors in
possesses one eigenvalue which is 1 but all the vectors in ![]() are possible eigenvectors.
are possible eigenvectors.
You should also have noticed that some matrices don’t have any real eigenvalues, i.e., none of the vectors keep their direction after transformation. This is the case for the matrix:
![]()
Additionally, the matrix:
![]()
has only one eigenvalue while any vector which is a multiplier of
![]()
keeps its direction after transformation through the matrix ![]() . You should also notice that some matrices will have negative eigenvalues. In that case, the corresponding eigenvector will be transformed into the direction opposite to its original direction. See for example, the matrix:
. You should also notice that some matrices will have negative eigenvalues. In that case, the corresponding eigenvector will be transformed into the direction opposite to its original direction. See for example, the matrix:
![]()
Videos:
2.2.1 Basic Definitions
2.2.1.4 Tensor Product
Refer to this section.
2.2.1.7 Area Transformation
Refer to this section.

https://mecsimcalc.com/app/5787840/graphical_representation_of_the_eigenvalues_and_eigenvectors