Engineering at Alberta Courses » Video and Tutorials

Finite Element Analysis: Video and Tutorials

Problem 1: Deep Beam
Problem 2: Bernoulli vs. Timoshenko Cantilever Beams
Problem 3: Inflating a Balloon of Shell Elements
Problem 4: Elasto-Plastic Buckling of a Plate
Problem 5: Cylinder in Contact with a Rigid Plate
Problem 6: Elasto-Plastic Buckling of a 100x100x10 Steel Angle Under Bending and Normal Force
Example: How to Extract Data Along a Path in ABAQUS

Complete Linear Analysis – Theory and FEA Comparison

Linear Analysis in Mathematica:

Linear Analysis in ABAQUS:

Problem 1: Deep Beam

In this problem, we look at the analysis of a deep beam with a concentrated load in the middle. This problem serves as an introduction to for input and output of a PLANE solid linear elastic model into ABAQUS.

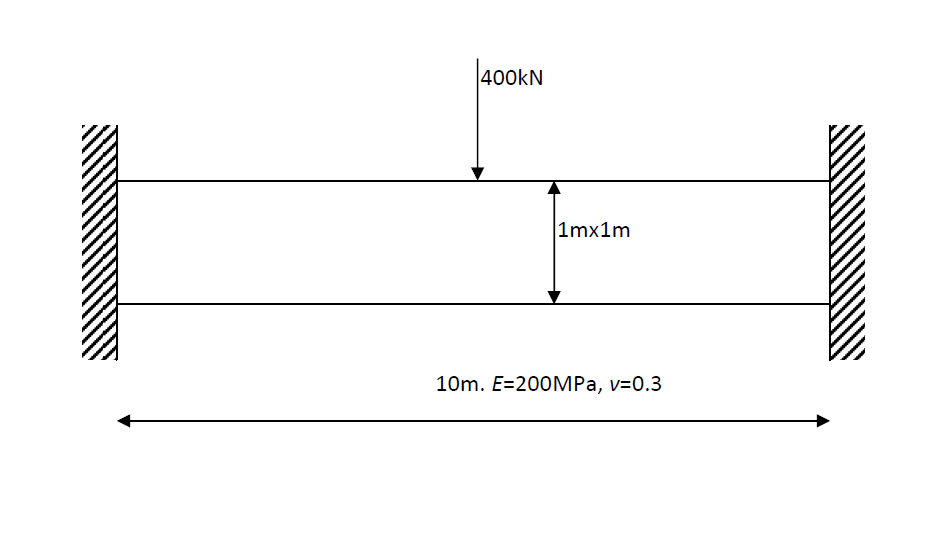
Problem description:

Mesh, Material, and Section:

Assembly:

Viewing Results:

Importing into Excel:

Problem 2: Bernoulli Vs. Timoshenko Cantilever Beams

The dimensions of the beam are $L=5m, b=0.25m, h=0.5m$ . The Material properties are: $E=200,000MPa$ , $G=77,000MPa$ . The concentrated load at the cantilever end is $P=10MN$ . The effective shear area for the Timoshenko beam is $A_y=k_1A=0.85A$ . Note that in some texts, the inverse of this relationship is given $A_y=\frac{A}{k_2}=\frac{A}{1.18}$ . The exact solution for the vertical displacement at the cantilever end for the Bernoulli beam is given by:

$v = \frac{PL^3}{3EI} = 0.8m$

While that for the Timoshenko beam is given by:

$v = \frac{PL^3}{3EI} + \frac{PL}{GA_y} = 0.806m$

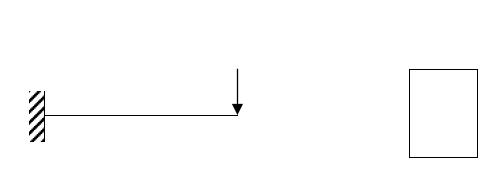
Problem description:

Part 2:

Part 3:

Part 4:

Part 5:

Problem 3: Inflating a Balloon of Shell Elements

In this example we look at using hyperelastic material and shell elements for a highly nonlinear problem.

Part 1:

Part 2:

Part 3:

Part 4:

Part 5:

Problem 4: Elasto-Plastic Buckling of a Plate

A plate that is thick and wide is loaded until it buckles around the minor axis. The problem will be considered as a plane problem. The Euler buckling load can be calculated as follows:

$P_{cr} = \frac{\pi^2 EI}{L^2} = 65.8N$

$\sigma_{cr} = \frac{P_{cr}}{A} = 0.658MPa$

The critical load per width of the plate is given by:

$\frac{P_{cr}}{b} = \frac{65.8}{50} = 1.316 \frac{N}{mm}$

The relationship between the true stress and the plastic strain is given by:

True Stress(MPa)	Plastic Strain
800	0
900	0.1%
1000	0.3%
1100	0.7%
1200	2%

Part 1:

Part 2:

Part 3:

Part 4:

Part 5:

Part 6:

Part 7:

Problem 5: Cylinder in Contact with a Rigid Plate

In this example, an arbitrary cylinder is resting on a rigid base. The friction coefficient is taken as 0.2.

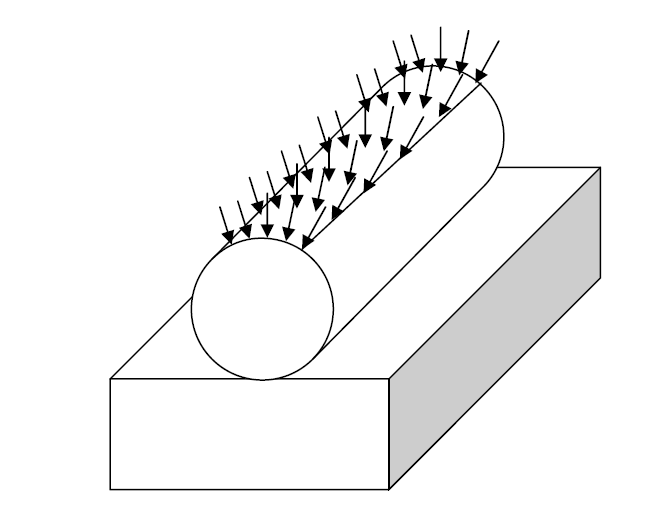
Part 1:

Part 2:

Part 3:

Part 4:

Problem 6: Elasto-Plastic Buckling of a 100X100X10 Steel Angle Under Bending and Normal Force

In this example, the Arc-Length method (Riks method in ABAQUS) is used to apply bending and normal force on a steel angle. The following are three videos created by three different students: