Engineering at Alberta Courses » A Method for Estimation of the Material Parameters of Hyperelastic Material Models in Relation to the Linear Elastic Material Model

Hyperelastic Materials: A Method for Estimation of the Material Parameters of Hyperelastic Material Models in Relation to the Linear Elastic Material Model

Given a particular form of the strain energy function, we present here a quick method by which the material parameters can be related to the shear modulus and the bulk modulus of a linear elastic material.

Shear Modulus

The material parameters of a hyperelastic material model can be related to the shear modulus of an elastic material as follows. First, a simple shear state of deformation is assumed:

$F=\left(\begin{array}{ccc} 1 & \alpha & 0 \\ 0 & 1 & 0 \\ 0& 0& 1 \end{array} \right)$

The engineering shear strain in this case is equal to $\alpha$ and $J=1$ . The matrix $C=F^TF$ is equal to:

$F^TF=\left(\begin{array}{ccc} 1 & \alpha & 0 \\ \alpha & 1+\alpha^2 & 0 \\ 0& 0& 1 \end{array} \right)$

The first and second invariants of $F^TF$ are:

$\begin{split} &I_1=3+\alpha^2\\ &I_2=\frac{1}{2}\left(I_1(F^TF)-I_1(F^TFF^TF)\right)=3+\alpha^2 \end{split}$

The following are examples of some of the compressible and incompressible material models listed above:

$\begin{split} &W_1=C_{10}\left(\overline{I_1} -3\right)+\frac{1}{D}(J-1)^2\\ &W_2=C_{10}\left(\overline{I_1} -3\right)+C_{01}\left(\overline{I_2}-3\right)+\frac{1}{D}(J-1)^2\\ &W_3=\mu_1(I_1(U^2)-3)\\ &W_4=\frac{\mu_1}{2}(I_1(U^2)-3)+\frac{\mu_2}{2}(I_2(U^2)-3) \end{split}$

For each of these material models, the corresponding Cauchy stress matrix has the form:

$\begin{split} & \sigma_1= \left(\begin{array}{ccc} \frac{4}{3}C_{10}\alpha^2 & 2C_{10}\alpha & 0 \\ 2C_{10}\alpha & -\frac{2}{3}C_{10}\alpha^2 & 0 \\ 0& 0& -\frac{2}{3}C_{10}\alpha^2 \end{array} \right)\\ & \sigma_2= \left(\begin{array}{ccc} \frac{2}{3}(2C_{10}+C_{01})\alpha^2 & 2(C_{10}+C_{01})\alpha & 0 \\ 2(C_{10}+C_{01})\alpha & -\frac{2}{3}(C_{10}+2C_{01})\alpha^2 & 0 \\ 0& 0& -\frac{2}{3}(C_{10}+2C_{01})\alpha^2 \end{array} \right)\\ & \sigma_3= \left(\begin{array}{ccc} 2\mu_1(1+\alpha^2)+p & 2\mu_1\alpha & 0 \\ 2\mu_1\alpha & 2\mu_1+p & 0 \\ 0& 0& 2\mu_1+p \end{array} \right)\\ & \sigma_4= \left(\begin{array}{ccc} \mu_1(1+\alpha^2)+\mu_2(2+\alpha^2)+p & (\mu_1+\mu_2)\alpha & 0 \\ (\mu_1+\mu_2)\alpha & \mu_1+2\mu_2+p & 0 \\ 0& 0& \mu_1+2\mu_2+p \end{array} \right) \end{split}$

For linear elastic materials, the shear stress component $\sigma_{12}$ and the engineering shear strain component $\gamma_{12}$ are related by the relationship: $\sigma_{12}=G\gamma_{12}$ . By investigating the component $\sigma_{12}$ in the above matrices and by setting $\gamma_{12}=\alpha$ , the relationship between the shear modulus $G$ and the given material parameters are as follows:

For material 1: $\sigma_{12}=2C_{10}\alpha\Rightarrow C_{10}=\frac{G}{2}$
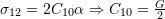
For material 2: $\sigma_{12}=2(C_{10}+C_{01})\alpha\Rightarrow C_{10}+C_{01}=\frac{G}{2}$
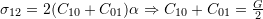
For material 3: $\sigma_{12}=2\mu_1\alpha\Rightarrow \mu_1=\frac{G}{2}$
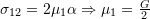
For material 4: $\sigma_{12}=(\mu_1+\mu_2)\alpha\Rightarrow \mu_1+\mu_2=G$

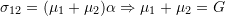
Bulk Modulus

The material parameters of a hyperelastic material model can be related to the bulk modulus of an elastic material as follows. First, a spherical state of deformation is assumed:

$F=\left(\begin{array}{ccc} \alpha & 0 & 0 \\ 0 & \alpha & 0 \\ 0& 0& \alpha \end{array} \right)$

$J=\alpha^3$ . The matrix $C=F^TF$ is equal to:

$F^TF=\left(\begin{array}{ccc} \alpha^2 & 0 & 0 \\ 0 & \alpha^2 & 0 \\ 0& 0& \alpha^2 \end{array} \right)$

The first and second invariants of $F^TF$ are:

$\begin{split} &I_1=3\alpha^2\\ &I_2=\frac{1}{2}\left(I_1(F^TF)-I_1(F^TFF^TF)\right)=3\alpha^4 \end{split}$

The following are examples of some of the compressible material models listed above:

$\begin{split} &W_1=C_{10}\left(\overline{I_1} -3\right)+\frac{1}{D}(J-1)^2\\ &W_2=C_{10}\left(\overline{I_1} -3\right)+C_{01}\left(\overline{I_2}-3\right)+\frac{1}{D}(J-1)^2 \end{split}$

For each of these material models, the Cauchy stress has the form:

$\begin{split} &\sigma_1=\frac{2}{D}(\alpha^3-1)I\\ &\sigma_2=\frac{2}{D}(\alpha^3-1)I \end{split}$

For linear elastic materials, the hydrostatic stress component $p=\frac{\sigma_{11}+\sigma_{22}+\sigma_{33}}{3}$ is related to the engineering volumetric strain $\varepsilon_v=\frac{\delta V}{V}$ by the relationship $p=K\varepsilon_v$ . In the deformation described in this problem, the volumetric strain is equal to $J-1=\alpha^3-1$ , therefore, an estimate of the material constant $D$ for the above materials is given as: