Open Educational Resources

Calculus: Vector Calculus

Fields

Let D\subset\mathbb{R}^n be a set. Scalar, vector or tensor valued functions defined on D are denoted as scalar, vector or tensor fields respectively. If D is a subset of \mathbb{R}^3 and if \phi:D\rightarrow\mathbb{R}, u:D\rightarrow\mathbb{R}^3, and T:D\rightarrow\mathbb{M}^3 are scalar, vector and second-order tensor fields respectively, then by choosing a coordinate system defined by the orthonormal basis set B=\{e_1,e_2,e_3\}, then the arguments of the functions can be chosen to be the cartesian coordinates x_i such that \forall x\in D:

    \[ \phi(x)=\phi(x_1,x_2,x_3)\qquad u(x)=u(x_1,x_2,x_3)\qquad T(x)=T(x_1,x_2,x_3) \]

FIeld Derivatives

Change of Basis

By the results of the change of basis section, if another orthonormal basis set B'=\{e'_1,e'_2,e'_3\} is chosen, where Q is the transformation matrix defined as Q_{ij} = e'_i\cdot e_j, then the components in the new orthonormal basis set x' are related to the original components using the relationship:

    \[ x'=Qx \]

The matrix Q is related to the derivatives of the components of x' with respect to the original components x as follows:

    \[ Q_{ij}=\frac{\partial x'_i}{\partial x_j} \]

and since Q^T=Q^{-1} we also have:

    \[ Q_{ij}=\frac{\partial x_j}{\partial x'_i} \]

The above relationships will be useful when calculating the derivatives of other fields.

Gradient of a Scalar Field

Let \phi:D\subset\mathbb{R}^3\rightarrow\mathbb{R} be a scalar field, \phi is said to be continuous at c\in D if

    \[ \lim_{x\rightarrow c}\phi(x)=\phi(c) \]

Alternatively, \phi is continuous at c if \forall n\in \mathbb{R}^3 we have:

    \[ \lim_{h\rightarrow 0}|\phi(c+hn)-\phi(c)|=0 \]

\phi is said to be continuous if it is continuous at every point.
\phi is said to be differentiable if there exists a vector field denoted \nabla \phi or \mathrm{grad}\phi such that \forall x\in D, \forall n\in\mathbb{R}^3

    \[ \lim_{h\rightarrow 0}\left|\frac{\phi(x+hn)-\phi(x)}{h}-\nabla\phi\cdot n\right|=0 \]

The gradient vector field \nabla\phi is unique since if another vector field b satisfies the above equation, we have \forall n\in\mathbb{R}^3:

    \[ 0\leq|\nabla\phi\cdot n-b\cdot n|\leq \left|\frac{\phi(x+hn)-\phi(x)}{h}-\nabla\phi\cdot n\right|+\left|\frac{\phi(x+hn)-\phi(x)}{h}-b\cdot n\right|\rightarrow 0 \]

Since n is arbitrary, we have:

    \[ \nabla\phi=b \]

By replacing n with the basis vectors e_1,e_2 and e_3, then the components of the vector \nabla\phi have the form:

    \[ \nabla\phi = \left(\begin{array}{c} \frac{\partial\phi}{\partial x_1}\\ \frac{\partial\phi}{\partial x_2}\\ \frac{\partial\phi}{\partial x_3} \end{array} \right) \]

The components of the vector (\nabla\phi)' using an orthonormal basis set B'=\{e'_1,e'_2,e'_3\} are related to the components of \nabla\phi using the relationship:

    \[\begin{split} (\nabla\phi)' &= \left(\begin{array}{c} \frac{\partial\phi}{\partial x'_1}\\ \frac{\partial\phi}{\partial x'_2}\\ \frac{\partial\phi}{\partial x'_3} \end{array} \right) = \left(\begin{array}{c} \frac{\partial\phi}{\partial x_1}\frac{\partial x_1}{\partial x'_1}+\frac{\partial\phi}{\partial x_2}\frac{\partial x_2}{\partial x'_1}+\frac{\partial\phi}{\partial x_3}\frac{\partial x_3}{\partial x'_1}\\ \frac{\partial\phi}{\partial x_1}\frac{\partial x_1}{\partial x'_2}+\frac{\partial\phi}{\partial x_2}\frac{\partial x_2}{\partial x'_2}+\frac{\partial\phi}{\partial x_3}\frac{\partial x_3}{\partial x'_2}\\ \frac{\partial\phi}{\partial x_1}\frac{\partial x_1}{\partial x'_3}+\frac{\partial\phi}{\partial x_2}\frac{\partial x_2}{\partial x'_3}+\frac{\partial\phi}{\partial x_3}\frac{\partial x_3}{\partial x'_3} \end{array} \right)\\ & = \left(\begin{array}{ccc} \frac{\partial x_1}{\partial x'_1} & \frac{\partial x_2}{\partial x'_1} &\frac{\partial x_3}{\partial x'_1}\\ \frac{\partial x_1}{\partial x'_2} & \frac{\partial x_2}{\partial x'_2} &\frac{\partial x_3}{\partial x'_2}\\ \frac{\partial x_1}{\partial x'_3} & \frac{\partial x_2}{\partial x'_3} &\frac{\partial x_3}{\partial x'_3} \end{array} \right) \left(\begin{array}{c} \frac{\partial \phi}{\partial x_1}\\ \frac{\partial \phi}{\partial x_2}\\ \frac{\partial \phi}{\partial x_3} \end{array} \right)\\ &=Q \nabla\phi \end{split} \]

Therefore, the transformation of the vector \nabla \phi follows the same rule for the change of basis for vectors in the Euclidean vector space \mathbb{R}^3.

The directional derivative of the scalar field \phi in the direction of a fixed unit vector n\in\mathbb{R}^3 (i.e., \| n\| = 1) is defined as:

    \[ \mathrm{directional derivative}=\lim_{h\rightarrow 0}\frac{\phi(x+hn)-\phi(x)}{h}=\nabla\phi\cdot n \]

The maximum value for the directional derivative is attained when n is chosen in the direction of the vector \nabla \phi. On the other hand, the directional derivative in the direction of any vector that is normal (perpendicular) to \nabla \phi is obviously zero. In other words, the vector field \nabla \phi points towards the direction of the maximum change of the scalar field \phi.

Partial Derivatives and Differentiability

Note that if the partial derivatives of \phi exist, they do not guarantee that \phi is differentiable at every point. Consider the following counter example:

    \[ \phi= \begin{cases} 0 & \text{if }(x,y)=(0,0)\\ \frac{3x^2y}{x^2+y^2} & \text{otherwise} \end{cases} \]

The function \phi is continuous at every point including at (x,y)=(0,0), why?. In addition, the partial derivatives with respect to x and y are defined as:

    \[\begin{split} \frac{\partial\phi}{\partial x} &= \begin{cases} 0, & \text{if }(x,y)=(0,0)\\ \frac{6xy^3}{(x^2+y^2)^2}, & \text{otherwise} \end{cases}\\ \frac{\partial\phi}{\partial y}&= \begin{cases} 0, & \text{if }(x,y)=(0,0)\\ \frac{3x^2(x^2-y^2)}{(x^2+y^2)^2}, & \text{otherwise} \end{cases} \end{split} \]

However, \phi is not differentiable at (x,y)=(0,0). Consider the direction n=(1,1), then the directional derivative along n at the point (x,y)=(0,0) can be evaluated using the dot product:

    \[ n\cdot \left(\frac{\partial\phi}{\partial x},\frac{\partial\phi}{\partial y}\right)_{(x,y)=(0,0)} =0 \]

However, the limit along the line x=y gives a non zero value:

    \[ \lim_{\alpha\rightarrow 0}\left(\frac{\phi(\alpha,\alpha)-\phi(0,0)}{\alpha}\right)=\frac{3\alpha^3}{2\alpha^3}=\frac{3}{2}\neq 0 \]

It is worth noting that the partial derivative \frac{\partial\phi}{\partial y} is not continuous at (x,y)=(0,0). Since

    \[ \lim_{x\rightarrow 0}\frac{\partial\phi}{\partial y}=\lim_{x\rightarrow 0}\frac{3x^2(x^2-y^2)}{(x^2+y^2)^2}=\frac{0}{y^4}=0 \]

while

    \[ \lim_{y\rightarrow 0}\frac{\partial\phi}{\partial y}=\lim_{y\rightarrow 0}\frac{3x^2(x^2-y^2)}{(x^2+y^2)^2}=\frac{3x^4}{x^4}=3 \]

therefore, \frac{\partial\phi}{\partial y} is not continuous.

However, there is a theorem from vector calculus that states that \phi is differentiable if and only if the partial derivatives exist and are continuous. The proof of this theorem can be found in multivariate calculus textbooks.

Gradient of a Vector Field

Let u:D\subset\mathbb{R}^3\rightarrow\mathbb{R}^3 be a vector field, u is said to be continuous at c\in D if

    \[ \lim_{x\rightarrow c}u(x)=u(c) \]

Alternatively, u is continuous at c if \forall n\in \mathbb{R}^3 we have:

    \[ \lim_{h\rightarrow 0}\|u(c+hn)-u(c)\|=0 \]

Alternatively, u is continuous at c if every component u_i of the vector field u is a continuous scalar function.
u is said to be continuous if it is continuous at every point.

u is said to be differentiable if there exists a tensor field denoted \nabla u or \mathrm{grad}(u) such that \forall x\in D, \forall n\in\mathbb{R}^3

    \[ \lim_{h\rightarrow 0}\left\|\frac{u(x+hn)-u(x)}{h}-\nabla u(n)\right\|=0 \]

The gradient tensor field \nabla u is unique since if another tensor field B satisfies the above equation, we have \forall n\in\mathbb{R}^3:

    \[ 0\leq\|\nabla u(n)-B(n)\|\leq \left\|\frac{u(x+hn)-u(x)}{h}-\nabla u(n)\right\|+\left\|\frac{u(x+hn)-u(x)}{h}-B(n)\right\|\rightarrow 0 \]

Since n is arbitrary, we have:

    \[ \nabla u=B \]

By replacing n with the basis vectors e_1,e_2 and e_3, then the components of the tensor \nabla u have the form:

    \[ \nabla u = \left(\begin{array}{ccc} \frac{\partial u_1}{\partial x_1}& \frac{\partial u_1}{\partial x_2}&\frac{\partial u_1}{\partial x_3}\\ \frac{\partial u_2}{\partial x_1}& \frac{\partial u_2}{\partial x_2}&\frac{\partial u_2}{\partial x_3}\\ \frac{\partial u_3}{\partial x_1}& \frac{\partial u_3}{\partial x_2}&\frac{\partial u_3}{\partial x_3} \end{array} \right) \]

The components of the tensor (\nabla u)' using an orthonormal basis set B'=\{e'_1,e'_2,e'_3\} are related to the components of \nabla u using the relationship:

    \[ (\nabla u)'_{ij}=\frac{\partial u'_i}{\partial x'_j}=\sum_{k,l=1}^3\frac{\partial Q_{ik}u_k}{\partial x_l}\frac{\partial x_l}{\partial x'_j}=\sum_{k,l=1}^3 Q_{ik}\frac{\partial u_k}{\partial x_l}Q_{jl} \]

Therefore,

    \[ (\nabla u)'=Q (\nabla u) Q^T \]

I.e.,the transformation of the tensor \nabla u follows the same rule for the change of basis for tensors in the Euclidean vector space \mathbb{R}^3.

Similar to the scalar fields, the existence of the partial derivatives of a vector field does not guarantee the differentiability except when the partial derivatives are continuous.

Divergence of a Vector Field

Let u:D\subset\mathbb{R}^3\rightarrow\mathbb{R}^3 be a differentiable vector field, then, the divergence of u denoted by \mathrm{div}(u) is a scalar field defined as:

    \[ \mathrm{div}(u)=\mathrm{Trace}(\nabla u) \]

Using the properties of the trace function, the divergence operator can be written in terms of the components of \nabla u as follows:

    \[ \mathrm{div}(u)=\frac{\partial u_1}{\partial x_1}+\frac{\partial u_2}{\partial x_2}+\frac{\partial u_3}{\partial x_3} \]

Gradient of a Tensor Field

In order to assess continuity and differentiability of tensors, we first have to define what we mean by the size or norm of a tensor. If M:\mathbb{R}^n\rightarrow\mathbb{R}^m, then we can define the following norm function on such tensors as follows:

    \[ \|M\|=\sup_{\|u\|=1,u\in\mathbb{R}^n}\|Mu\| \]

In other words, the norm of M, is the supremum of the norms of the vectors Mu where u is a unit vector and u\in\mathbb{R}^n. One should check that this definition satisfies the required properties of a norm function as shown in the definitions of linear vector spaces.
Let T:D\subset\mathbb{R}^3\rightarrow\mathbb{M}^3 be a tensor field, T is said to be continuous at c\in D if

    \[ \lim_{x\rightarrow c}T(x)=T(c) \]

Alternatively, T is continuous at c if \forall n\in \mathbb{R}^3 we have:

    \[ \lim_{h\rightarrow 0}\|T(c+hn)-T(c)\|=0 \]

Alternatively, T is continuous at c if every component T_{ij} of the tensor field T is a continuous scalar function.
T is said to be continuous if it is continuous at every point.

T is said to be differentiable if there exists a third-order tensor field denoted \nabla T or \mathrm{grad}(T) such that \forall x\in D, \forall n\in\mathbb{R}^3

    \[ \lim_{h\rightarrow 0}\left\|\frac{T(x+hn)-T(x)}{h}-\nabla T(n)\right\|=0 \]

The gradient third-order tensor field \nabla T is unique since if another tensor field C satisfies the above equation, we have \forall n\in\mathbb{R}^3:

    \[ 0\leq\|\nabla T(n)-C(n)\|\leq \left\|\frac{T(x+hn)-T(x)}{h}-\nabla T(n)\right\|+\left\|\frac{T(x+hn)-T(x)}{h}-C(n)\right\|\rightarrow 0 \]

Since n is arbitrary, we have:

    \[ \nabla T=C \]

By replacing n with the basis vectors e_1,e_2 and e_3, then the components of the tensor \nabla T have the form:

    \[ (\nabla T)_{ijk} = \frac{\partial T_{ij}}{\partial x_k} \]

The components of the tensor (\nabla T)' using an orthonormal basis set B'=\{e'_1,e'_2,e'_3\} are related to the components of \nabla T using the relationship:

    \[ (\nabla T)'_{ijk}=\frac{\partial T'_{ij}}{\partial x'_k}=\sum_{l,m,n=1}^3\frac{\partial Q_{il}T_{lm}Q_{jm}}{\partial x_n}\frac{\partial x_n}{\partial x'_k}=\sum_{l,m,n=1}^3 Q_{il}Q_{jm}Q_{kn}\frac{\partial T_{lm}}{\partial x_n} \]

I.e.,the transformation of the tensor \nabla u follows the same rule for the change of basis for second-order tensors in the Euclidean vector space \mathbb{R}^3.

Similar to the scalar fields, the existence of the partial derivatives of a vector field does not guarantee the differentiability except when the partial derivatives are continuous.

DIvergence of a Tensor Field

Let T:D\subset\mathbb{R}^3\rightarrow\mathbb{R}^3 be a differentiable vector field, then, the divergence of T denoted by \mathrm{div}(T) is a vector field defined such that \forall n\in\mathbb{R}^3:

    \[ \mathrm{div}(T)\cdot n=\mathrm{div}(Tn) \]

By replacing n with the basis vectors e_1,e_2 and e_3, then the components of the vector \mathrm{div} T have the form:

    \[ \mathrm{div}(T) = \left(\begin{array}{c} \frac{\partial T_{11}}{\partial x_1}+\frac{\partial T_{21}}{\partial x_2}+\frac{\partial T_{31}}{\partial x_3}\\ \frac{\partial T_{12}}{\partial x_1}+\frac{\partial T_{22}}{\partial x_2}+\frac{\partial T_{32}}{\partial x_3}\\ \frac{\partial T_{13}}{\partial x_1}+\frac{\partial T_{23}}{\partial x_2}+\frac{\partial T_{33}}{\partial x_3}\end{array}\right) \]

Or in compact form:

    \[ (\mathrm{div}(T))_i = \sum_{j=1}^3\frac{\partial T_{ji}}{\partial x_j} \]

It should be noted that in some texts, the divergence operator is defined as \mathrm{div}T^T. The choice between the two definitions is a matter of convention.

Curl of a Vector Field

Let u:D\subset\mathbb{R}^3\rightarrow\mathbb{R}^3 be a smooth vector field. The curl of u at a point x\in D is defined as the vector such that \forall n\in\mathbb{R}^3:

    \[ \mbox{curl}(u)\cdot n=\mbox{div}(u\times n) \]

If u has the components u_1, u_2, and u_3 in an orthonormal basis set, then, by setting n=e_1, e_2, and e_3 in the above formula, the components of \mbox{curl}(u) are shown to have the following form:

    \[\mbox{curl}(u)=\left(\begin{array}{c}\frac{\partial u_3}{\partial x_2}-\frac{\partial u_2}{\partial x_3}\\\frac{\partial u_1}{\partial x_3}-\frac{\partial u_3}{\partial x_1}\\\frac{\partial u_2}{\partial x_1}-\frac{\partial u_1}{\partial x_2}\end{array}\right)\]

or in a compact form:

    \[ (\mbox{curl}(u))_i=\varepsilon_{ijk}\frac{\partial u_k}{\partial x_j} \]

Laplacian of a Scalar Field

Let \phi:D\subset\mathbb{R}^3\rightarrow\mathbb{R} be a twice differentiable scalar field. The Lacplacian of \phi denoted by \nabla^2\phi at any point x\in D is defined as the divergence of the gradient of \phi:

    \[ \nabla^2\phi=\mathrm{div} \left(\nabla \phi\right)=\frac{\partial^2 \phi}{\partial x_1^2}+\frac{\partial^2 \phi}{\partial x_2^2}+\frac{\partial^2 \phi}{\partial x_3^2} \]

The Divergence Theorem

The divergence theorem which is also known as the Gauss’ theorem or Green’s theorem is a useful tool that relates volume integrals of gradients of functions to surface integrals of those functions. In physical terms, the divergence theorem states that the change of a continuous differentiable quantity inside a closed volume is due to the flux of this quantity entering or exiting through the boundary. The continuity ensures that there are not sinks or sources inside the volume. The mathematical theorem is as follows:

Statement

Suppose D\subset\mathbb{R}^3 is a compact set with a piecewise smooth boundary S=\partial D and n:S\rightarrow \mathbb{R}^3 is the vector field defining the outward normal to the boundary S. Let \phi:D\rightarrow \mathbb{R} be a continuous and differentiable scalar field and x_1, x_2, x_3 define the coordinates of a point x\in D. Then, the divergence theorem states:

    \[\begin{split} \int\limits_D \! \frac{\partial\phi}{\partial x_1} \,\mathrm{d}x &=\oint\limits_{S} \! \phi n_1 \,\mathrm{d}S\\ \int\limits_D \! \frac{\partial\phi}{\partial x_2} \,\mathrm{d}x &=\oint\limits_{S} \! \phi n_2 \,\mathrm{d}S\\ \int\limits_D \! \frac{\partial\phi}{\partial x_3} \,\mathrm{d}x &=\oint\limits_{S} \! \phi n_3 \,\mathrm{d}S \end{split} \]

where \mathrm{d}x and \mathrm{d}S are volume and surface elements respectively. The proof of the divergence theorem is straightforward but technical. It can be found in many vector calculus textbooks.

Variations

The statement of the divergence theorem above can be used to show the following consequences or variations of the divergence theorem. Assuming the same variables in the statement above and given continuous and differentiable vector and tensor fields u:D\rightarrow\mathbb{R}^3 and T:D\rightarrow\mathbb{M}^3 respectively then:

    \[\begin{split} \int\limits_D \! \nabla\phi \,\mathrm{d}x &=\oint\limits_{S} \! \phi n \,\mathrm{d}S\\ \int\limits_D \! \nabla u \,\mathrm{d}x &=\oint\limits_{S} \! u\otimes n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} u \,\mathrm{d}x &=\oint\limits_{S} \! u \cdot n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} u \,\mathrm{d}x &=\oint\limits_{S} \! u \cdot n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} (\phi u) \,\mathrm{d}x &=\oint\limits_{S} \! \phi u \cdot n \,\mathrm{d}S\\ \int\limits_D \! \nabla (Tu) \,\mathrm{d}x &=\oint\limits_{S} \! (Tu)\otimes n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} T \,\mathrm{d}x &=\oint\limits_{S} \! T^T n \,\mathrm{d}S\\ \int\limits_D \! \mathrm{div} (Tu) \,\mathrm{d}x &=\oint\limits_{S} \! u\cdot T^T n \,\mathrm{d}S \end{split} \]

Useful Formulas

The following are useful formulas relating the various definitions above:

    \[\begin{split} \mathrm{div}(\phi u) &=u\cdot \nabla \phi + \phi \mathrm{div}u\\ \mathrm{div}(T u) &=u\cdot \mathrm{div} T + \mathrm{Trace}(T\nabla u)\\ \mathrm{div}(\phi T) &=T^T\nabla \phi + \phi\mathrm{div}(T)\\ \nabla (\phi u) &=u\otimes \nabla \phi + \phi \nabla u\\ \int\limits_D \! \mbox{curl}{u} \,\mathrm{d}x &=\oint\limits_{S} \! n\times u \,\mathrm{d}S \end{split} \]

Note that the definitions and the results in this section can be naturally extended to \mathbb{R}^n for an arbitrary n.

Comma Notation

To simplify the expressions in vector calculus, comma notation can sometimes be used to replace the expression for partial differentiation. Consider a scalar field \phi:D\subset\mathbb{R}^3\rightarrow\mathbb{R}. Then, the partial derivative of \phi with respect to any of the components x_1, x_2, and x_3, can be written as:

    \[ \frac{\partial \phi}{\partial x_i}=\phi_{,i} \]

If u:D\subset\mathbb{R}^3\rightarrow\mathbb{R}^3 and T:D\subset\mathbb{R}^3\rightarrow\mathbb{M}^3 are vector and tensor fields, respectively, then, the following simplified comma notation expressions can be used (where the Einstein summation convention is also used for repeated indices):

    \[\begin{split} (\nabla u)_{ij}&=\frac{\partial u_i}{\partial x_j}=u_{i,j}\\ \mathrm{div}(u)&=\frac{\partial u_i}{\partial x_i}=u_{i,i}\\ (\mathrm{div}(T))_i&=\frac{\partial T_{ji}}{\partial x_j}=T_{ji,j}\\ (\mbox{curl}u)_i&=\varepsilon_{ijk}\frac{\partial u_k}{\partial x_j}=\varepsilon_{ijk}u_{k,i}\\ \nabla^2\phi&=\phi_{,ii} \end{split} \]

Examples and Problems

Example 1

Consider the set D=\{(x,y)|-4\leq x\leq 4, -4\leq y\leq 4\}\subset\mathbb{R}^2 and the scalar field \phi:D\rightarrow \mathbb{R}:

    \[ \phi=5x^2-7x(y+3)-5y^2 \]

The gradient of \phi can be calculated as:

    \[ \nabla \phi = \left(\begin{array}{c} 10x-7(y+3)\\ -7x-10y \end{array} \right) \]

The following tool shows the surface plot and the contour plot of \phi. The vector plot of \nabla \phi is also drawn and then superimposed on top of the contour plot. Notice how the arrows are perpendicular to the contour lines! The maximum directional derivative of \phi at the point x_0=0,y_0=0 is calculated to be along n_1=\{-1,0\} and n_2=\{0,1\}. The maximum directional derivative is in the direction perpendicular to the contour line while the minimum directional derivative which is equal to zero is in the direction along (parallel) to the contour line. The tool also lets you choose a point p=\{x_0,y_0\} and the angle \theta of the direction of the vector n and calculates the directional derivative \nabla \phi\cdot n at that point.

(interactive activity placeholder) VectorCalculus/phi1.jsp

View Mathematica Code

x0 = 0;
y0 = 0;
Clear[x, y];
fi = 5 x^2-7 x (y + 3)-5 y^2;
gradfi = {D[fi, x], D[fi, y]};
gradfic = gradfi /. {x -> x0, y -> y0};
p0 = {x0, y0};
n1 = gradfic/Norm[gradfic];
n2 = {n1[[2]], -n1[[1]]};
Ar1 = Graphics[Arrow[{p0, p0 + n1}]];
Ar2 = Graphics[Arrow[{p0, p0 + n2}]];
Artext1 = Graphics[Text["n1", p0 + n1 + 0.2 n1]];
Artext2 = Graphics[Text["n2", p0 + n2 + 0.2 n2]];
a = Plot3D[fi, {x, -4, 4}, {y, -4, 4}];
b = ContourPlot[fi, {x, -4, 4}, {y, -4, 4}, ContourLabels -> True];
c = VectorPlot[gradfi, {x, -4, 4}, {y, -4, 4}];
Grid[{{"3 D Plot", "Contour Plot", "Gradient of \[Phi] plot"}, 
{Show[a], Show[b], Show[c]}, {"Contour Plot superimposed over Gradient of \\[Phi] plot", 
SpanFromLeft}, {Show[b, c, ImageSize -> "Medium"], SpanFromLeft}, 
{"Directional Derviative at {0, 0} in the direction of n1 and n2", SpanFromLeft}, 
{Show[b, Ar1, Artext1, Ar2, Artext2, ImageSize -> "Medium"], SpanFromLeft}, 
{Grid[{{"\[Del]\[Phi] at (0, 0) =", gradfic // MatrixForm}}, 
Spacings -> 0], SpanFromLeft}, {Grid[{{"n1=", N[n1] // MatrixForm, ",\[Del]\[Phi]\[CenterDot]n1 =", 
gradfic . n1}}, Spacings -> 0], SpanFromLeft}, {Grid[{{"n2 = ", 
N[n2] // MatrixForm, ", \[Del]\[Phi]\[CenterDot]n2 =", gradfic . n2}}, Spacings -> 0], SpanFromLeft}}]

View Python Code

from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
from sympy import diff, Matrix, lambdify
%matplotlib notebook
x,y=sp.symbols("x y")
f=5*x**2-7*x*(y+3)-5*y**2
fx=diff(f,x)
fy=diff(f,y)
v=Matrix([fx,fy])
#numpy equivalent F function
F=lambdify((x,y),f)
Fx=lambdify((x,y),fx)
Fy=lambdify((x,y),fy)
#ranges for plotting
xrange = np.arange(-4, 4, .5)
yrange = np.arange(-4, 4, .5)
X, Y = np.meshgrid(xrange, yrange)
Z = F(X,Y)
DFx=Fx(X,Y)
DFy=Fy(X,Y)
# 3D plot
fig = plt.figure(figsize=(6,6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X,Y,Z)
plt.title('3D Plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# Contour plot
fig = plt.figure()
ax = fig.add_subplot(111)
cp = ax.contourf(X,Y,Z)
fig.colorbar(cp)
plt.title('Contour Plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
# Gradient plot
fig = plt.figure()
ax = fig.add_subplot(111)
ax.quiver(X, Y, DFx,DFy)
plt.title('Gradient of \u03A6 Plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
# Contour Plot superimposed over Gradient
fig = plt.figure()
ax = fig.add_subplot(111)
ax.contourf(X,Y,Z)
ax.quiver(X, Y, DFx, DFy)
plt.title('Contour Plot superimposed over Gradient of \u03A6 plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
#Directional Derviative at {0,0}
fig = plt.figure()
ax = fig.add_subplot(111)
ax.contourf(X,Y,Z)
x_0 = np.where(xrange == 0)[0][0]
y_0 = np.where(yrange == 0)[0][0]
phi = np.array([[DFx.item(x_0,y_0)],[DFy.item(x_0, y_0)] ])
ax.quiver(X[x_0, y_0], Y[x_0, y_0], DFx.item(x_0,y_0),DFy.item(x_0, y_0))
plt.title('Directional Derviative at {0,0}')
ax.set_xlabel('X')
ax.set_ylabel('Y')
#outputs 
print("Delta \u03A6 at (0,0) =\n", phi)

Video

Vector Calculus Quiz

Problems

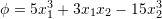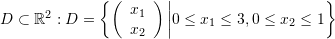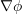  1. Let \phi=5x_1^3+3x_1x_2-15x_2^3 be a scalar field defined over the set D\subset\mathbb{R}^2:D=\left\{\left(\begin{array}{c}x_1\\x_2\end{array}\right)\bigg| 0\leq x_1\leq 3, 0\leq x_2\leq 1\right\}. Evaluate and indicate the order (whether it is a scalar, vector, or tensor) of the gradient of \phi, the Laplacian of \phi, the gradient of \nabla \phi, and the divergence of the gradient of 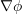\nabla \phi. Use Mathematica to visualize \phi and \nabla \phi. 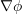Why is the gradient of 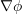\nabla \phi always symmetric independent of the choice of the smooth function \phi?
  2. Use the definitions in this section to show the equalities in Useful Formulas above.
  3. Use the divergence theorem defined above to show the last three equalities shown in the Variations of the divergence theorem shown above.

Leave a Reply

Your email address will not be published.