Single Degree of Freedom Systems: Equivalent Mass and Equivalent Stiffness
We have seen that the form of the equation of motion for a simple spring{mass system is
![]()
Similarly, for a simple pendulum (undergoing small motions), the equation of motion can be written as
![]()
which has a very similar form. In general, for any linear undamped single degree of freedom system the equation of motion can be expressed in the form
![]()
where ![]() is the chosen coordinate in the problem.
is the chosen coordinate in the problem. ![]() and
and ![]() are known as the effective mass and effective stiffness respectively. Note that once
are known as the effective mass and effective stiffness respectively. Note that once ![]()
![]() are known, the natural frequency of the system can be found easily as
are known, the natural frequency of the system can be found easily as
![]()
Effective Mass
So far we have found ![]() and
and ![]() using Newton’s Laws or energy methods. There are other ways to determine these quantities which may be easier in some situations. One method used to determine
using Newton’s Laws or energy methods. There are other ways to determine these quantities which may be easier in some situations. One method used to determine ![]() for a system is to note that the kinetic energy of the SDOF system can be written as
for a system is to note that the kinetic energy of the SDOF system can be written as
![]()
where again ![]() is the chosen coordinate. Once the expression for the kinetic energy of the system is found,
is the chosen coordinate. Once the expression for the kinetic energy of the system is found, ![]() can be found by inspection.
can be found by inspection.
EXAMPLE
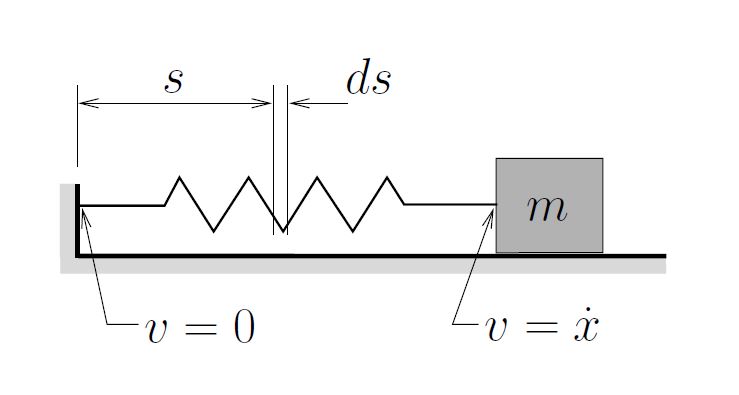
While in many situations it is appropriate to ignore the mass of a spring in a vibration analysis, any real spring will have some mass which may, in certain situations, need to be taken into account. Estimate the effect that the mass of the spring ![]() has on the natural frequency of the simple spring–mass system shown below.
has on the natural frequency of the simple spring–mass system shown below.

Begin by estimating the kinetic energy of the spring making some simplifying assumptions:
- The mass of the spring is uniformly distributed along the length of the spring.
- The velocity of any point on the spring is proportional to its distance from the fixed end.
Equivalent Stiffness – Stiffness and Flexibility Approaches
To determine the effective stiffness ![]() , it can similarly be shown that the potential energy of the system is
, it can similarly be shown that the potential energy of the system is
![]()
so that ![]() can also be found by inspection once the potential energy expression has been determined. However, there are also other approaches, stiffness and flexibility methods, that can be used to determine
can also be found by inspection once the potential energy expression has been determined. However, there are also other approaches, stiffness and flexibility methods, that can be used to determine ![]() based on statics. These approaches are similar and are based on the idea that the force
based on statics. These approaches are similar and are based on the idea that the force ![]() applied to a system (in the positive coordinate
applied to a system (in the positive coordinate ![]() direction) and the resulting deflection
direction) and the resulting deflection ![]() (of the coordinate) are related by
(of the coordinate) are related by
![]()
In the stiffness approach, the system is given a unit displacement and the force ![]() required to maintain this deformed configuration is determined through statics. The effective stiffness is then given by
required to maintain this deformed configuration is determined through statics. The effective stiffness is then given by
![]()
In the flexibility approach, a unit load is applied to the system and the resulting deflection ![]() is determined using statics. The effective stiffness is then given by
is determined using statics. The effective stiffness is then given by
![]()
In both of these approaches it is important to realize that the force ![]() and the displacement
and the displacement ![]() are always measured in the positive coordinate direction. Also note that if the coordinate is a rotation (measured in radians), the same approach can be used replacing the force
are always measured in the positive coordinate direction. Also note that if the coordinate is a rotation (measured in radians), the same approach can be used replacing the force ![]() with a torque
with a torque ![]() . The details are summarized as follows.
. The details are summarized as follows.
For single degree of freedom systems, the process of finding the effective stiffness can be generalized as either a stiffness or flexibility approach, both of which are static in nature and are based on the definition
![]()
Stiffness Approach
Linear Displacements: Displace the system such that it has a unit displacement in the positive coordinate direction. Then, using statics, determine the force ![]() required in the positive coordinate direction to maintain this deflected state. Then, since
required in the positive coordinate direction to maintain this deflected state. Then, since ![]() and
and ![]() ,
,
![]()
Angular Displacements: Displace the system such that it has a unit angular displacement (![]() ) in the positive coordinate direction. Then, using statics, determine the torque
) in the positive coordinate direction. Then, using statics, determine the torque ![]() required in the positive coordinate direction to maintain this deflected state. Then, since
required in the positive coordinate direction to maintain this deflected state. Then, since ![]() and
and ![]() ,
,
![]()
Flexibility Approach
Linear Displacements: Apply a unit load in the positive coordinate direction and determine, through statics, the resulting deflection ![]() in the positive coordinate direction. Then, since
in the positive coordinate direction. Then, since ![]() and
and ![]() ,
,
![]()
Angular Displacements: Apply a unit torque in the positive coordinate direction and determine, through statics, the resulting angular deflection ![]() in the positive coordinate direction. Then, since
in the positive coordinate direction. Then, since ![]() and
and ![]() ,
,
![]()
EXAMPLES
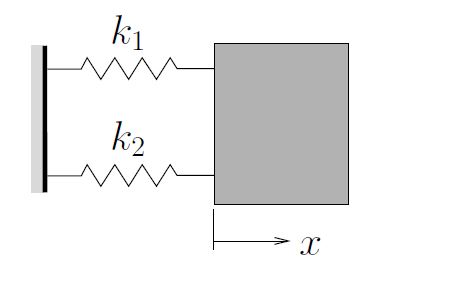
- Springs in Parallel
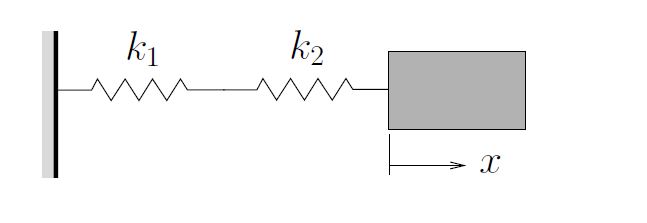
2. Springs in Series
3. Mass at End of Cantilever (Lateral Motions)

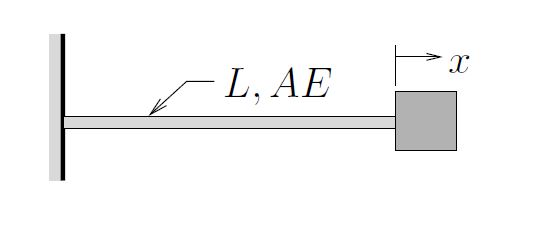
4. Mass at End of Cantilever (Axial Motions)
5. Mass at End of Cantilever (Torsional Motions)

Occasionally we need to modify these approaches slightly when a “unit” force or displacement would significantly change the geometry of the system resulting in a nonlinearity. In such cases we apply “small” forces or displacements instead of unit ones. Another way to think of this is to still apply a unit load, but the “unit” of the load is smaller (i.e. apply 1μN instead of 1 N). A similar approach could be taken for displacements.
EXAMPLE
In the diagram below a spring supports a mass and makes an angle ![]() with the direction of motion. Determine the effective stiffness of the spring in this situation. Assume that only small motions occur.
with the direction of motion. Determine the effective stiffness of the spring in this situation. Assume that only small motions occur.
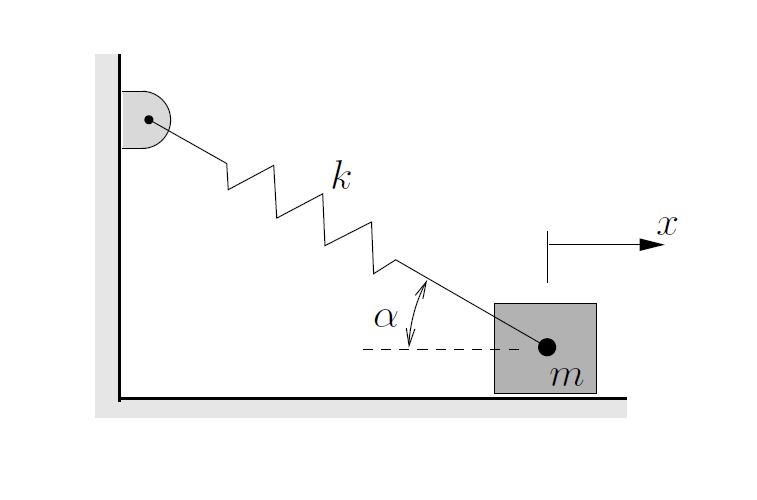
EXAMPLE
Determine the natural frequency for the system shown below. The double pulley set has a mass moment of inertia ![]() about its center
about its center ![]() . A mass
. A mass ![]() is supported by a light inextensible cable.
is supported by a light inextensible cable.
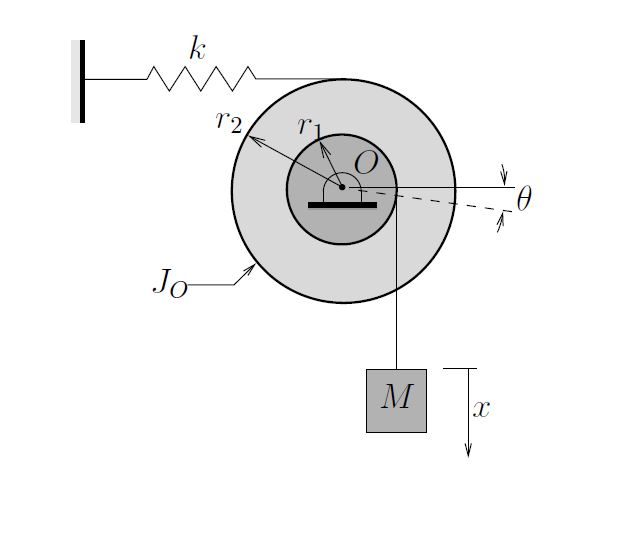
EXAMPLE
Determine the effective stiffness ![]() of the system shown below. Neglect the mass of the bar
of the system shown below. Neglect the mass of the bar ![]() .
.

EXAMPLE
Determine the effective stiffness ![]() of the system shown below. Neglect the mass of the bar
of the system shown below. Neglect the mass of the bar ![]() .
.
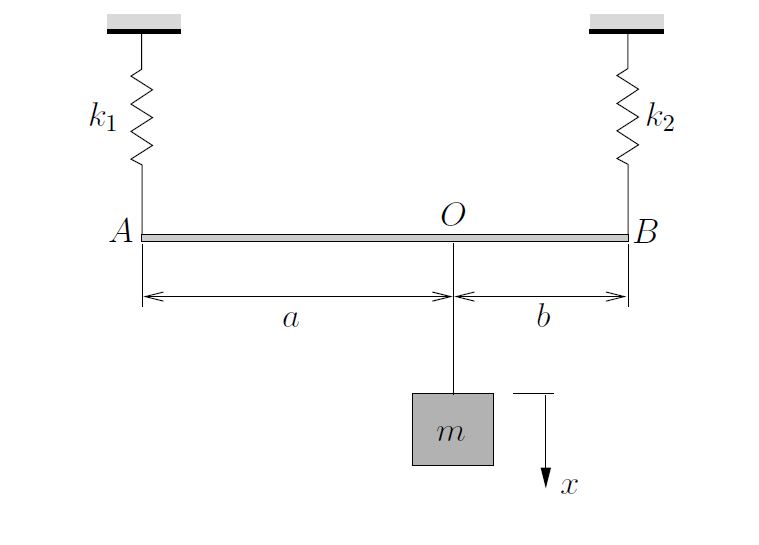
EXAMPLE
A block of mass ![]() is supported by a cable and pulley system as shown below. Pulleys
is supported by a cable and pulley system as shown below. Pulleys ![]() and
and ![]() are pinned to the block while pulley
are pinned to the block while pulley ![]() is attached to a rigid support by a spring of stiffness
is attached to a rigid support by a spring of stiffness ![]() . Neglecting the mass of the pulleys and treating the cable as inextensible, determine
. Neglecting the mass of the pulleys and treating the cable as inextensible, determine
- the effective stiffness of the cable and pulley system,
- the natural frequency of free vibrations.
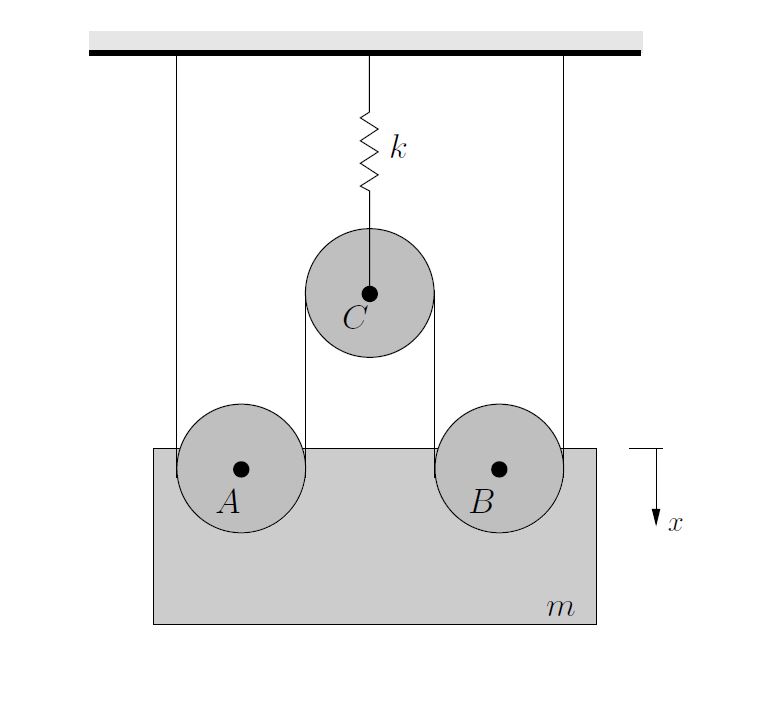
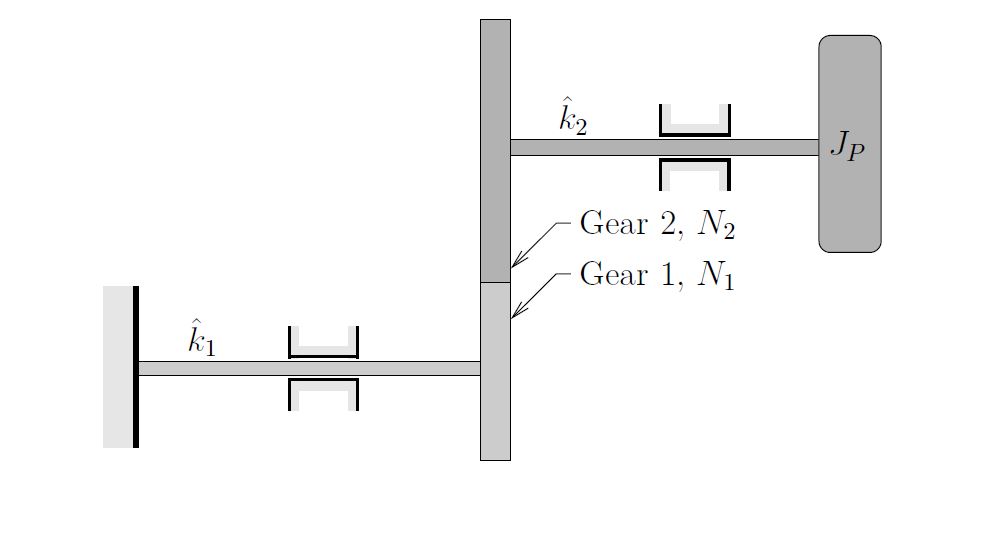
EXAMPLE
In the system shown below, a rotor with polar moment of inertia ![]() is supported by a combination of shafts and gears as shown. Shafts 1 and 2 have torsional stiffnesses
is supported by a combination of shafts and gears as shown. Shafts 1 and 2 have torsional stiffnesses ![]() and
and ![]() respectively while gears 1 and 2 have
respectively while gears 1 and 2 have ![]() and
and ![]() teeth respectively.
teeth respectively.
Determine the effective stiffness ![]() for this system and the natural frequency of free vibrations. Neglect the masses of the gears.
for this system and the natural frequency of free vibrations. Neglect the masses of the gears.

Excellent