Engineering at Alberta Courses » Response of Spring

Transient Vibrations: Response of Spring–Mass System to a Ramp Function

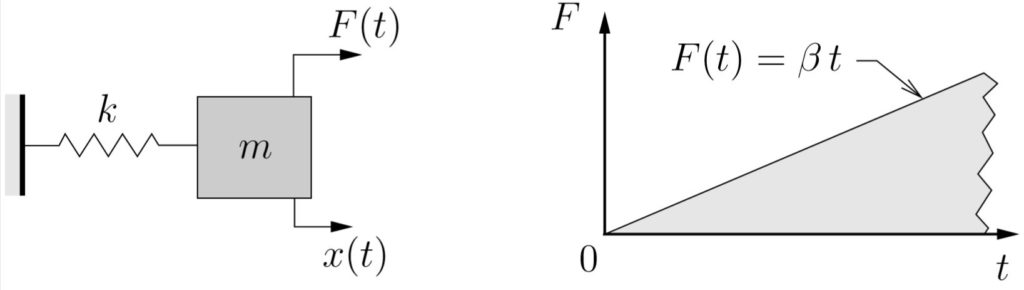
The equation of motion in this case is

$\begin{equation*}m \ddot{x} + k x = \beta t\end{equation*}$

It is easy to verify by direct substitution that the particular solution is

$\begin{equation*}x_P(t) = \frac{\beta}{k} t\end{equation*}$

so the total solution is

(7.5) $\begin{equation*}\label{eq:RampResponseGeneral}x(t) = A \sin{pt} + B \cos{pt} + \frac{\beta}{k} t\end{equation*}$

If the initial conditions are

$\begin{equation*}x(0) = 0, \qquad \dot{x}(0) = 0\end{equation*}$

then $A = \dfrac{-\beta}{k p}$ and $B=0$ so we get

(7.6) $\begin{equation*}\label{eq:RampResponseIC}\boxed{x(t) = \frac{\beta}{k p} \Bigl(p t - \sin{pt} \Bigr)}\end{equation*}$

which is illustrated below.

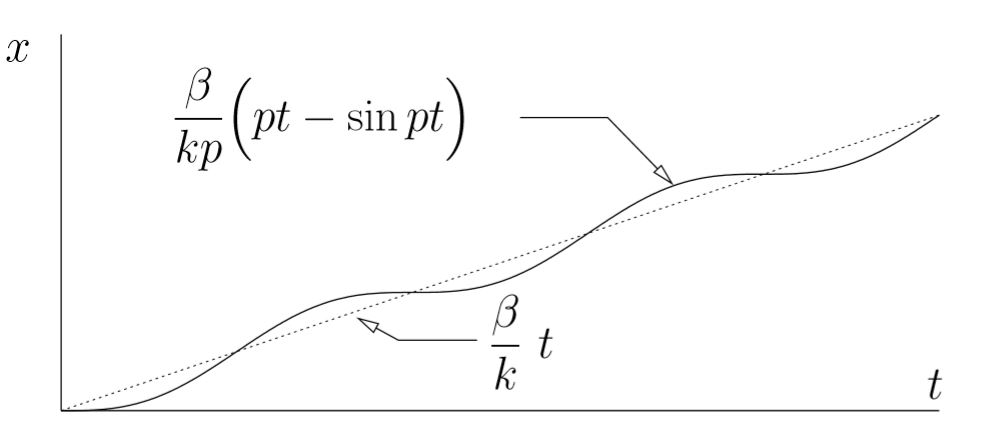
Response to Ramp Function with x(0) = ˙x(0) = 0

We can interpret this response as an oscillation with amplitude $\dfrac{\beta}{k p}$ about an equilibrium position that is increasing linearly with time.

Open Educational Resources

Transient Vibrations: Response of Spring–Mass System to a Ramp Function

Leave a Reply Cancel reply